IIT JEE Main Maths -Unit 11 -Lines and Skew lines- Exam Style Questions- New Syllabus

Question

Let $\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}$ be $L_1$ and $\dfrac{x-2}{3}=\dfrac{y-4}{4}=\dfrac{z-5}{5}$ be $L_2$. Then which of the following points lies on the line of the shortest distance between $L_1$ and $L_2$?

$(1)\ \left(-\dfrac{5}{3},\ 7,\ 1\right)$

$(2)\ \left(\dfrac{1}{2},\ 3,\ \dfrac{1}{3}\right)$

$(3)\ \left(-\dfrac{8}{3},\ 1,\ \dfrac{1}{3}\right)$

$(4)\ \left(-\dfrac{14}{3},\ 3,\ \dfrac{22}{3}\right)$

▶️ Answer/Explanation

Let $P(2\lambda + 1,\ 3\lambda + 2,\ 4\lambda + 3)$ be a point on $L_1$ and $Q(3\mu + 2,\ 4\mu + 4,\ 5\mu + 5)$ be a point on $L_2$.

The direction ratios of $\overrightarrow{PQ}$ are $3\mu – 2\lambda + 1,\ 4\mu – 3\lambda + 2,\ 5\mu – 4\lambda + 2$.

For $\overrightarrow{PQ} \perp L_1$:

$(3\mu – 2\lambda + 1)\cdot 2 + (4\mu – 3\lambda + 2)\cdot 3 + (5\mu – 4\lambda + 2)\cdot 4 = 0$

$\Rightarrow 38\mu – 29\lambda + 16 = 0$ …(1)

For $\overrightarrow{PQ} \perp L_2$:

$(3\mu – 2\lambda + 1)\cdot 3 + (4\mu – 3\lambda + 2)\cdot 4 + (5\mu – 4\lambda + 2)\cdot 5 = 0$

$\Rightarrow 50\mu – 38\lambda + 21 = 0$ …(2)

Solving (1) and (2): $\lambda = \dfrac{1}{3},\ \mu = -\dfrac{1}{6}$.

So $P = \left(\dfrac{5}{3},\ 3,\ \dfrac{13}{3}\right)$, $Q = \left(\dfrac{10}{3},\ 0,\ \dfrac{25}{6}\right)$.

The equation of $PQ$ is $\dfrac{x – 5/3}{5/3} = \dfrac{y – 3}{-3} = \dfrac{z – 13/3}{-1/6}$.

The point $\left(-\dfrac{14}{3},\ 3,\ \dfrac{22}{3}\right)$ lies on $PQ$.

The correct answer is $(4)\ \left(-\dfrac{14}{3},\ 3,\ \dfrac{22}{3}\right)$.

Question

Let $ L_1 : \frac{x-1}{3} = \frac{y-1}{-1} = \frac{z-1}{0} $ and $ L_2 : \frac{x-2}{\alpha} = \frac{y}{2} = \frac{z-4}{0} $, $ \alpha \in \mathbb{R} $, be two lines, which intersect at the point $ B $. If $ P $ is the foot of perpendicular from the point $ A(1, 1, -1) $ on $ L_2 $, then the value of $ 26 \alpha (PB)^2 $ is ____.

▶️ Answer/Explanation

Ans. (216)

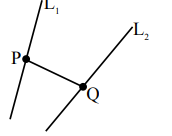
Sol. Point $ B $

$ (3\lambda + 1, -\lambda + 1, -1) \equiv (2\mu + 2, 0, \alpha \mu – 4) $

$ 3\lambda + 1 = 2\mu + 2 $

$ -\lambda + 1 = 0 $

$ -1 = \alpha \mu – 4 $

$ \lambda = 1, \mu = 1, \alpha = 3 $

$ B(4, 0, -1) $

Let Point $ P $ is $ (2\delta + 2, 0, 3\delta – 4) $

Dr’s of $ AP < 2\delta + 1, -1, 3\delta – 3 > $

$ AP \perp L_2 \Rightarrow \delta = \frac{7}{13} $

$ P\left( \frac{40}{13}, 0, -\frac{31}{13} \right) $

$ (PB)^2 = 26 \times 3 \times \left( \frac{144}{169} + \frac{324}{169} \right) = 216 $

Question

The perpendicular distance, of the line $\frac{x-1}{2} = \frac{y-2}{1} = \frac{z-3}{-2}$ from the point $P(2, -10, 1)$, is:
(1) 6
(2) $5\sqrt{2}$
(3) $3\sqrt{5}$
(4) $4\sqrt{3}$

▶ Answer/Explanation

Ans. (3)
Sol.

$P(2,-10, 1)$ $A$
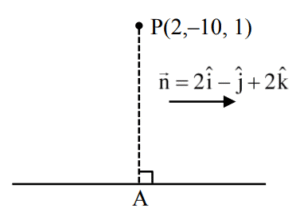
$\frac{x-1}{2} = \frac{y-2}{1} = \frac{z-3}{-2}$ (let)
$(2\lambda + 1, -\lambda – 2, 2\lambda – 3)$
$PA.n = 0$
$\Rightarrow (2\lambda – 1)2 + (-\lambda + 8)(-1) + (2\lambda – 4)2 = 0$
$\Rightarrow 4\lambda – 2 + \lambda – 8 + 4\lambda – 8 = 0$
$\Rightarrow 9\lambda – 18 = 0$ $\Rightarrow \lambda = 2$
$\therefore A(5, -4, 1)$
$\therefore AP = \sqrt{3^2 + 6^2 + 0^2} = \sqrt{45} = 3\sqrt{5}$

Question

9. Let P be the foot of the perpendicular from the point Q(10, –3, –1) on the line
$ \frac{x – 3}{7} = \frac{y – 2}{-1} = \frac{z – 1}{-2} $.
Then the area of the right angled triangle PQR, where R is the point (3, –2, 1), is

(1) $ 9\sqrt{15} $

(2) $30 $

(3) $ 8\sqrt{15} $

(4) $ 3\sqrt{30} $

▶️ Answer/Explanation

Ans. (4)

Sol.

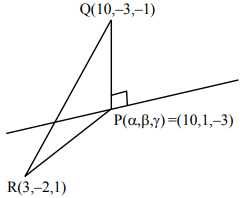
Let point on line be $ P(7\lambda + 3, -\lambda + 2, -2\lambda + 1) $.

Direction ratios of $ QP \Rightarrow (7\lambda – 7, -\lambda + 5, -2\lambda – 2) $

Since $ QP \perp \text{line} \Rightarrow (7\lambda – 7)(7) + (-\lambda + 5)(-1) + (-2\lambda – 2)(-2) = 0 $

$ 54\lambda – 54 = 0 \Rightarrow \lambda = 1 $

$ \therefore P = (10, 1, -3) $

$ \overrightarrow{PQ} = 4\hat{j} + 2\hat{k} $, $ \overrightarrow{PR} = -7\hat{i} – 3\hat{j} + 4\hat{k} $

Area $ = \frac{1}{2} |\overrightarrow{PQ} \times \overrightarrow{PR}| = \frac{1}{2} \sqrt{(0)^2 + (4)^2 + (2)^2} = 3\sqrt{30} $

IIT JEE Main Maths -Unit 11 -Lines and Skew lines- Exam Style Questions- New Syllabus

Resources

Members

Company