IIT JEE Main Maths -Unit 12 - Vectors and Scalars- Exam Style Questions- New Syllabus

Question

Let $ \mathbf{c} $ be the projection vector of $ \mathbf{b} = \lambda \hat{i} + 4 \hat{k} $, $ \lambda > 0 $, on the vector $ \mathbf{a} = \hat{i} + 2 \hat{j} + 2 \hat{k} $. If $ |\mathbf{a} + \mathbf{c}| = 7 $, then the area of the parallelogram formed by the vectors $ \mathbf{b} $ and $ \mathbf{c} $ is ______.

▶️ Answer/Explanation

Ans. (16)

Sol. $ \mathbf{c} = \frac{(\mathbf{b} \cdot \mathbf{a})}{|\mathbf{a}|^2} \mathbf{a} $

$ = \frac{(\lambda + 8)}{9} (\hat{i} + 2 \hat{j} + 2 \hat{k}) $

$ |\mathbf{a} + \mathbf{c}| = 7 \Rightarrow \lambda = 4 $

Area of parallelogram = $ |\mathbf{b} \times \mathbf{c}| = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{4}{3} & \frac{8}{3} & \frac{8}{3} \\ 4 & 0 & 4 \end{vmatrix} = 16 $

Question

Let $a$ and $b$ be two unit vectors such that the angle between them is $\frac{\pi}{3}$. If $\lambda a + 2b$ and $3a – \lambda b$ are perpendicular to each other, then the number of values of $\lambda$ in $[-1, 3]$ is :
(1) 3
(2) 2
(3) 1
(4) 0

▶ Answer/Explanation

Ans. (4)
Sol.

$\hat{a}.\hat{b} = \frac{1}{2}$

$\text{Now } (\lambda\hat{a} + 2\hat{b}).(3\hat{a} – \lambda\hat{b}) = 0$

$3\lambda\hat{a}.\hat{a} – \lambda^2\hat{a}.\hat{b} + 6\hat{a}.\hat{b} – 2\lambda\hat{b}.\hat{b} = 0$

$3\lambda – \frac{\lambda^2}{2} + 3 – 2\lambda = 0$

$\lambda^2 – 2\lambda – 6 = 0$

$\lambda = 1 \pm \sqrt{7}$

$\Rightarrow \text{number of values} = 0$

Question

Let the arc AC of a circle subtend a right angle at the centre O. If the point B on the arc AC divides the arc AC such that
$ \frac{\text{length of arc AB}}{\text{length of arc BC}} = \frac{1}{5} $,
and $ \overrightarrow{OC} = \alpha \overrightarrow{OA} + \beta \overrightarrow{OB} $,
then $ (2\alpha – \beta) = $

(1) $ 2\sqrt{3} – 3 $

(2) $ 2\sqrt{3} $

(3) $ 5\sqrt{3} $

(4) $ 2 + \sqrt{3} $

▶️ Answer/Explanation

Ans. (1)

Sol.

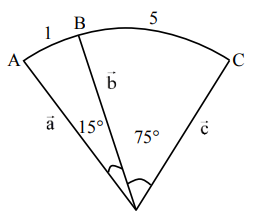
Let $ \angle AOB = 15^\circ $, $ \angle BOC = 75^\circ $.

Using vector relations:

$ \overrightarrow{OC} = \alpha \overrightarrow{OA} + \beta \overrightarrow{OB} $

$ \overrightarrow{a} \cdot \overrightarrow{c} = \alpha a^2 + \beta (\overrightarrow{a} \cdot \overrightarrow{b}) \Rightarrow 0 = \alpha + \beta \cos 15^\circ $ …(1)

$ \overrightarrow{b} \cdot \overrightarrow{c} = \alpha (\overrightarrow{b} \cdot \overrightarrow{a}) + \beta b^2 \Rightarrow \cos 75^\circ = \alpha \cos 15^\circ + \beta $ …(2)

From (1) and (2),

$ \cos 75^\circ = -\beta \cos^2 15^\circ + \beta $

$ \Rightarrow \beta = \frac{\sin 15^\circ}{\sin 15^\circ \cos 15^\circ} = 2 – \sqrt{3} $

$ \alpha = \frac{3 – \sqrt{3}}{2} $

$ \therefore (2\alpha – \beta) = 2\sqrt{3} – 3 $

Question

Let the position vectors of the vertices A, B and C of a tetrahedron ABCD be $\hat{i} + 2\hat{j} + \hat{k}$, $\hat{i} + 3\hat{j} – 2\hat{k}$ and $2\hat{i} – \hat{j} + \hat{k}$ respectively. The altitude from the vertex D to the opposite face ABC meets the median line segment through A of the triangle ABC at the point E. If the length of AD is $\frac{\sqrt{110}}{3}$ and the volume of the tetrahedron is $\frac{\sqrt{805}}{6\sqrt{2}}$, then the position vector of E is

(1) $\frac{1}{2} (\hat{i} + 4\hat{j} + 7\hat{k})$
(2) $\frac{1}{12} (7\hat{i} + 4\hat{j} – 3\hat{k})$
(3) $\frac{1}{6} (12\hat{i} + 12\hat{j} + \hat{k})$
(4) $\frac{1}{6} (7\hat{i} + 12\hat{j} + \hat{k})$

▶️ Answer/Explanation

Ans. (4)

Sol.

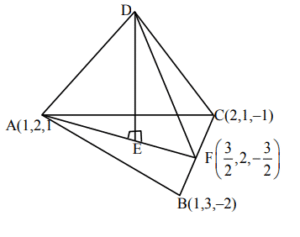
$\text{Area of }\triangle ABC = \frac{1}{2} |\overrightarrow{AB} \times \overrightarrow{AC}$

$= \frac{1}{2} |\hat{i} + 3\hat{j} + \hat{k}| = \frac{1}{2} \sqrt{35}$

$\text{volume of tetrahedron}$

$= \frac{1}{3} \times \text{Base area} \times h = \frac{\sqrt{805}}{6\sqrt{2}}$

$\frac{1}{3} \times \frac{1}{2} \sqrt{35} \times h = \frac{\sqrt{805}}{6\sqrt{2}}$

$h = \frac{\sqrt{23}}{\sqrt{2}}$

$\text{AE}^2 = \text{AD}^2 – \text{DE}^2 = \frac{13}{18} \quad : \quad \text{AE} = \frac{\sqrt{13}}{\sqrt{18}}$

$\overrightarrow{AE} = |\overrightarrow{AE}| \left( \frac{\hat{i} – 5\hat{k}}{\sqrt{26}} \right)$

$= \frac{\sqrt{13}}{\sqrt{18}} \cdot \frac{\hat{i} – 5\hat{k}}{\sqrt{26}}$

$= \frac{\sqrt{13} (\hat{i} – 5\hat{k})}{\sqrt{18} \cdot \sqrt{26}} = \frac{\hat{i} – 5\hat{k}}{6}$

$\text{P.V. of E} = \frac{\hat{i} – 5\hat{k}}{6} + \hat{i} + 2\hat{j} + \hat{k} = \frac{1}{6} (7\hat{i} + 12\hat{j} + \hat{k})$

IIT JEE Main Maths -Unit 12 - Vectors and Scalars- Exam Style Questions- New Syllabus

Resources

Members

Company