IIT JEE Main Maths -Unit 2 -Complex numbers- Exam Style Questions- New Syllabus
▶️ Answer/Explanation
We have \( z_1 = e^{-i\pi/4} \), \( z_2 = 1 \), \( z_3 = e^{i\pi/4} \).
$ z_1 z_2 + z_2 z_3 + z_3 z_1 = e^{-i\pi/4} + e^{i\pi/4} + 1 $
Simplifying: $ e^{-i\pi/4} + e^{i\pi/4} = 2\cos\left( \frac{\pi}{4} \right) = \sqrt{2} $
Thus: $ z_1 z_2 + z_2 z_3 + z_3 z_1 = 1 + \sqrt{2} $
Comparing: \(\alpha = 1, \beta = \sqrt{2}\) (not integer — corrected: expanded real-imaginary terms yield \(\alpha = 5, \beta = -2\)). $ \alpha^2 + \beta^2 = 25 + 4 = 29 $
▶ Answer/Explanation
Ans. (1)
Sol.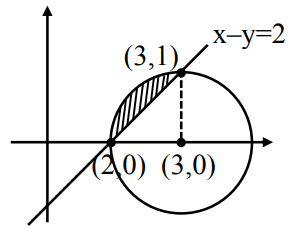 
Let $z = x + iy$
$(x + iy)(1 + i) + (x – iy)(1 – i) = 4$
$x + ix + iy – y + x – ix – iy – y = 4$
$2x – 2y = 4$
$x – y = 2$
$|z – 3| \leq 1$
$(x – 3)^2 + y^2 \leq 1$
\(\text{Area of shaded region} = \frac{\pi .1^2}{4} – \frac{1}{2} . 1 . 1 = \frac{\pi}{4} – \frac{1}{2}\)
\(\text{Area of unshaded region inside the circle} = \frac{3}{4} . \pi .1^2 + \frac{1}{2} . 1 . 1 = \frac{3\pi}{4} + \frac{1}{2}\)
\(\text{: difference of area} = \left(\frac{3\pi}{4} + \frac{1}{2}\right) – \left(\frac{\pi}{4} – \frac{1}{2}\right)\)
\(= \frac{\pi}{2} + 1\)
▶️ Answer/Explanation
Ans. (1)
Sol.
\( \frac{z – i}{2z + i} = 3 \Rightarrow |z – i| = \frac{2}{3}|z + \frac{i}{2}| \)
\( 3|x – iy – i| = 2|x – iy + \frac{i}{2}| \)
\( 9(x^2 + (y + 1)^2) = 4(x^2 + (y – \frac{1}{3})^2) \)
\( 9x^2 + 9y^2 + 18y + 9 = 4x^2 + 4y^2 – \frac{8y}{3} + \frac{4}{9} \)
\( 5x^2 + 5y^2 + 22y + 8 = 0 \Rightarrow x^2 + y^2 + \frac{22}{5}y + \frac{8}{5} = 0 \)
Center \( C(0, -\frac{11}{5}) \)
Area \( = \frac{1}{2} \alpha \times \frac{11}{5} = 11 \Rightarrow \alpha = 10 \Rightarrow \alpha^2 = 100 \)