IIT JEE Main Maths -Unit 8 -Definite integrals- Exam Style Questions- New Syllabus

Question

Let the function,
$ f(x) = \begin{cases} -3ax – 2, & x < 1 \\ a^2 + bx, & x \geq 1 \end{cases} $
Be differentiable for all $ x \in \mathbb{R} $, where $ a > 1, b \in \mathbb{R} $. If the area of the region enclosed by $ y = f(x) $ and the line $ y = -20 $ is $ \alpha + \beta \sqrt{3} $, $ \alpha, \beta \in \mathbb{Z} $, then the value of $ \alpha + \beta $ is ____.

▶️ Answer/Explanation

Ans. (34)

Sol. $ f(x) $ is continuous and differentiable

at $ x = 1 $; LHL = RHL, LHD = RHD

$ -3a – 2 = a^2 + b, -6a = b $

$ a = 2, 1; b = -12 $

$ f(x) = \begin{cases} -6x – 2, & x < 1 \\ 4 – 12x, & x \geq 1 \end{cases} $

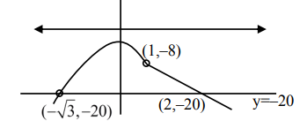
$\text{Area} = \int_{-\sqrt{3}}^{1} \big(-6x^2 – 2 – (-20)\big),dx ;+; \int_{1}^{2} \big(4 – 12x – (-20)\big),dx$

$= \int_{-\sqrt{3}}^{1} (-6x^2 + 18),dx ;+; \int_{1}^{2} (24 – 12x),dx$

$= \Big\( -2x^3 + 18x \Big${-\sqrt{3}}^{1} ;+; \Big$ 24x – 6x^2 \Big${1}^{2}\)

$\text{Area} = (16 + 12\sqrt{3}) + 6 = 22 + 12\sqrt{3}.$

So,
$\alpha = 22,\quad \beta = 12,\quad \alpha + \beta = 34.$

Question

Let $y = f(x)$ be the solution of the differential equation $\frac{dy}{dx} + \frac{xy^2 + x}{x^2 – 1} = \frac{4x}{1 – x^2}$, $-1 < x < 1$ such that $f(0) = 0$. If $6 \int_{-1/2}^{1/2} f(x) dx = \alpha \pi$, then $\alpha^2$ is equal to __________.

▶ Answer/Explanation

Ans. (27)

$ \text{I.F.} = e^{-\frac{1}{2} \int \frac{2x}{1 – x^2} \, dx} = e^{-\frac{1}{2} \ln(1 – x^2)} = \sqrt{1 – x^2} $

$ y \sqrt{1 – x^2} = \int (x^6 + 4x) \, dx = \frac{x^7}{7} + 2x^2 + c $

$\text{Given } y(0) = 0 \Rightarrow c = 0 $

$ y = \frac{\frac{x^7}{7} + 2x^2}{\sqrt{1 – x^2}} $

$\text{Now, } 6 \int_{0}^{\frac{1}{2}} \frac{\frac{x^7}{7} + 2x^2}{\sqrt{1 – x^2}} \, dx = 6 \int_{0}^{\frac{1}{2}} \frac{2x^2}{\sqrt{1 – x^2}} \, dx $

$ = 24 \int_{0}^{\frac{1}{2}} \frac{x^2}{\sqrt{1 – x^2}} \, dx $

\text{Put } $ x = \sin \theta $

$ dx = \cos \theta \, d\theta $

$ = 24 \int_{0}^{\frac{\pi}{6}} \frac{\sin^2 \theta}{\cos \theta} \cos \theta \, d\theta $

$ = 24 \int_{0}^{\frac{\pi}{6}} \frac{1 – \cos 2\theta}{2} \, d\theta = 12 \left[ \theta – \frac{\sin 2\theta}{2} \right]_{0}^{\frac{\pi}{6}} $

$ = 12 \left( \frac{\pi}{6} – \frac{\sqrt{3}}{4} \right) $

$ = 2\pi – 3\sqrt{3} $

$ \alpha^2 = (3\sqrt{3})^2 = 27 $

Question

1. The value of $ \displaystyle \int_{e^2}^{e^4} \frac{1}{x}
\left( \dfrac{e^{\left( (\log_e x)^2 + 1 \right)^{-1}}}
{e^{\left( (\log_e x)^2 + 1 \right)^{-1}} + e^{\left( (6 – \log_e x)^2 + 1 \right)^{-1}}} \right) dx $ is

(1) $ \log_e 2 $

(2) $ 2 $

(3) $ 1 $

(4) $ e^2 $

▶️ Answer/Explanation

Answer: (3)

Solution:

$\text{Ans. } (3)$

$\text{Sol. } \text{Let } \ln x = t \Rightarrow \frac{dx}{x} = dt$

$ I = \displaystyle\int_{2}^{4} \frac{e^{\frac{1}{1 + t^2}}}{e^{\frac{1}{1 + t^2}} + e^{\frac{1}{1 + (6 – t)^2}}} \, dt $

$ I = \displaystyle\int_{2}^{4} \frac{1}{1 + e^{\frac{1}{1 + (6 – t)^2} – \frac{1}{1 + t^2}}} \, dt $

$ I = \displaystyle\int_{2}^{4} \frac{1}{e^{\frac{1}{1 + (6 – t)^2}} + e^{\frac{1}{1 + t^2}}} \, dt $

$\text{Now, let’s replace } t \text{ by } (6 – t) \text{ in the integral.}$

$\therefore 2I = \displaystyle\int_{2}^{4} dt = (t)_{2}^{4} = 4 – 2 = 2$

$\Rightarrow I = 1$

Question

If the area of the larger portion bounded between the curves $x^2 + y^2 = 25$ and $y = |x – 1|$ is $\frac{1}{4} (b\pi + c)$, $b, c \in \mathbb{N}$, then $b + c$ is equal to ________

▶️ Answer/Explanation

Ans. (77)

Sol.

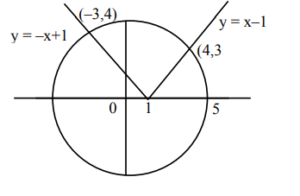
$ x^2 + y^2 = 25 $

$ x^2 + (x – 1)^2 = 25 \Rightarrow x = 4 $

$ x^2 + (-x + 1)^2 = 25 \Rightarrow x = -3 $

$ A = 25\pi – \int_{-3}^{4} \sqrt{25 – x^2} \, dx + \frac{1}{2} \times 4 \times 4 + \frac{1}{2} \times 3 \times 3 $

$ A = 25\pi + \frac{25}{2} \left[ \frac{x}{2} \sqrt{25 – x^2} + \frac{25}{2} \sin^{-1}\!\frac{x}{5} \right]_{-3}^{4} $

$ A = 25\pi + \frac{25}{2} \left[ \frac{1}{2} \left( 6 + \frac{25}{2} \sin^{-1}\!\frac{4}{5} + 6 + \frac{25}{2} \sin^{-1}\!\frac{3}{5} \right) \right] $

$ A = 25\pi + \frac{1}{2} \cdot \frac{25}{2} \cdot \frac{\pi}{2} \Rightarrow A = \frac{75\pi}{4} + \frac{1}{2} $

$ A = \frac{1}{4}(75\pi + 2) $

$ b = 75, \, c = 2 $

$ \therefore b + c = 75 + 2 = 77 $

IIT JEE Main Maths -Unit 8 -Definite integrals- Exam Style Questions- New Syllabus

Resources

Members

Company