IIT JEE Main Maths -Unit 8 -Integral as an antiderivative- Exam Style Questions- New Syllabus

Question

Let $ f : \mathbb{R} \to \mathbb{R} $ be a twice differentiable function such that $ f(x+y) = f(x)f(y) $ for all $ x, y \in \mathbb{R} $. If $ f'(0) = 4a $ and $ f”(x) – 3a f'(x) – f(x) = 0 $, $ a > 0 $, then the area of the region $ R = \{(x,y) \mid 0 \le y \le f(ax),\ 0 \le x \le 2\} $ is:

(1) $ e^2 – 1 $

(2) $ e^4 + 1 $

(3) $ e^4 – 1 $

(4) $ e^2 + 1 $

▶️ Answer/Explanation

Since $ f(x+y) = f(x)f(y) $, we have $ f(x) = e^{\lambda x} $. Given $ f'(0) = \lambda = 4a $, so $ f(x) = e^{4ax} $.

From $ f”(x) – 3a f'(x) – f(x) = 0 $, we get $ \lambda^2 – 3a\lambda – 1 = 0 $.

Substituting $ \lambda = 4a $, we have $ 16a^2 – 12a^2 – 1 = 0 \Rightarrow 4a^2 = 1 \Rightarrow a = \frac{1}{2} $.

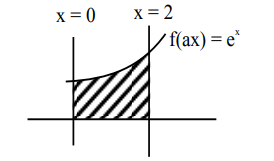
Then $ f(ax) = e^{x} $.

The required area is: $ \text{Area} = \int_{0}^{2} e^{x} \, dx = e^2 – 1 $

Hence, the correct answer is (1) $ e^2 – 1 $.

IIT JEE Main Maths -Unit 8 -Integral as an antiderivative- Exam Style Questions- New Syllabus

Resources

Members

Company