The Doppler Effect At Low Speed IB DP Physics Study Notes
The Doppler effect at low speeds IB DP Physics Study Notes
The Doppler effect at low speeds IB DP Physics Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on IB Physics syllabus with Students should understand
the nature of the Doppler effect for sound waves and electromagnetic waves
the representation of the Doppler effect in terms of wavefront diagrams when either the source or the observer is moving
the relative change in frequency or wavelength observed for a light wave due to the Doppler effect where the speed of light is much larger than the relative speed between the source and the observer
as given by \(\frac{\Delta f}{f} = \frac{\Delta \lambda}{\lambda} \approx \frac{v}{c}\)that shifts in spectral lines provide information about the motion of bodies like stars and galaxies in space
Standard level and higher level: 2 hours
Additional higher level: 2 hours
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 1
- IB DP Physics 2025 SL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
- IB DP Physics 2025 HL- IB Style Practice Questions with Answer-Topic Wise-Paper 2
1. The Nature of the Doppler Effect for Sound Waves and Electromagnetic Waves
The Doppler effect is the apparent change in frequency or wavelength of a wave when there is relative motion between the source and the observer. It occurs for both mechanical waves (like sound) and electromagnetic waves (like light).
For Sound Waves:
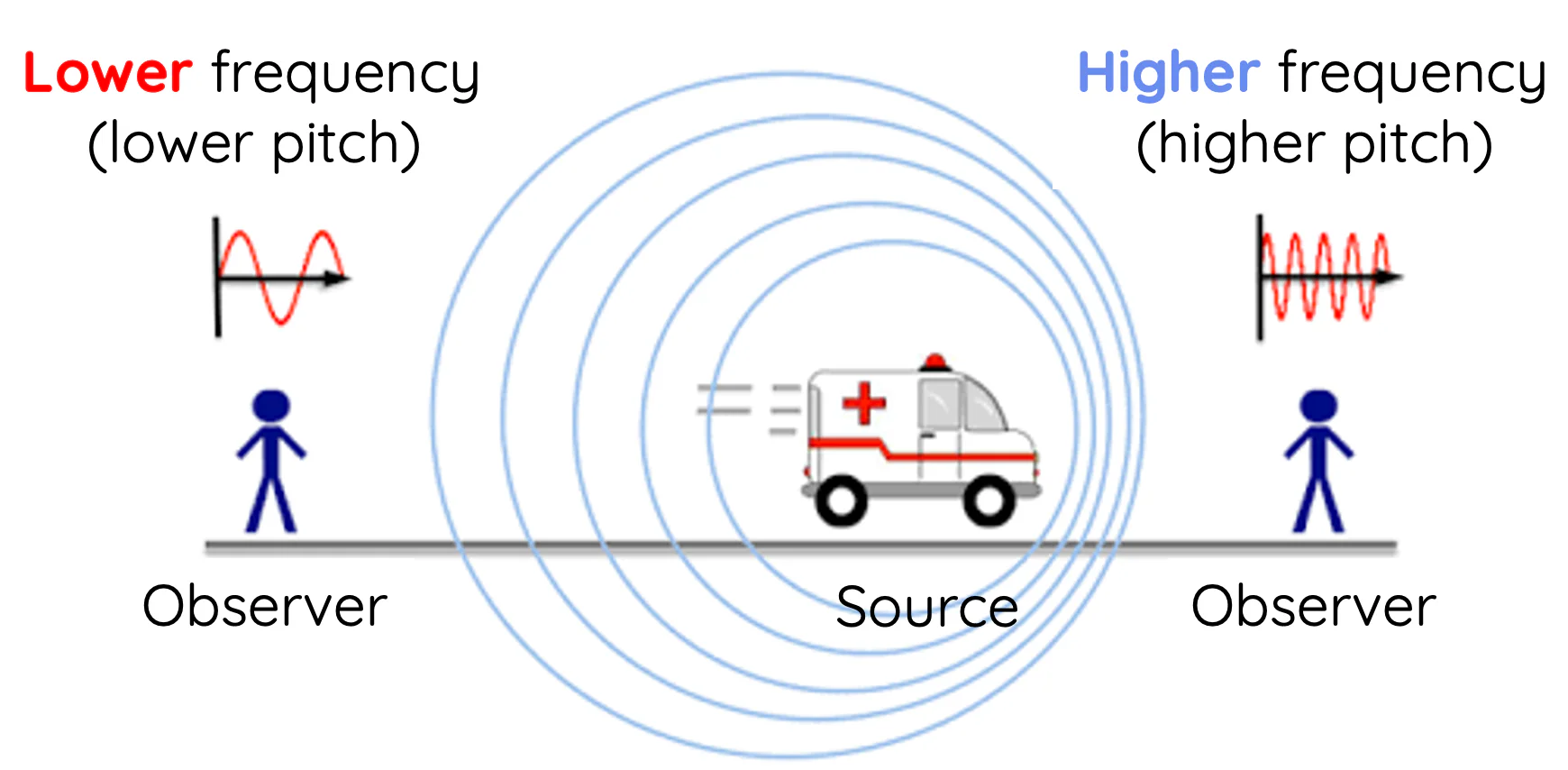
- The Doppler effect is heard as a change in pitch for example, the sound of an ambulance siren becomes higher as it approaches and lower as it moves away.
- It arises because the wavefronts are compressed or stretched due to the motion of the source or observer.
- The speed of sound in air is constant (\( \mathrm{v \approx 340 \ m/s} \)), so only the frequency changes when motion occurs.
For Electromagnetic Waves (Light):
- The Doppler effect causes a shift in the frequency (or wavelength) of light depending on relative motion.
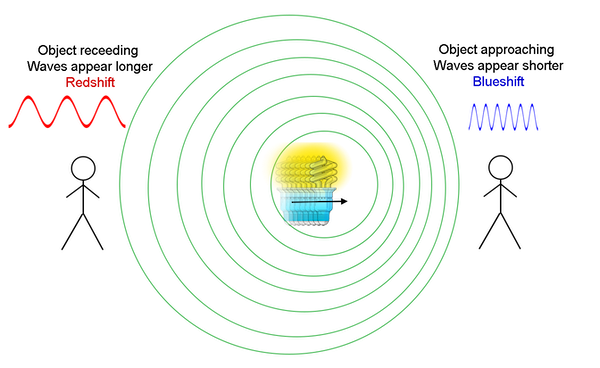
- If the source moves toward the observer → observed light shifts toward the blue (higher frequency).
- If the source moves away from the observer → light shifts toward the red (lower frequency).
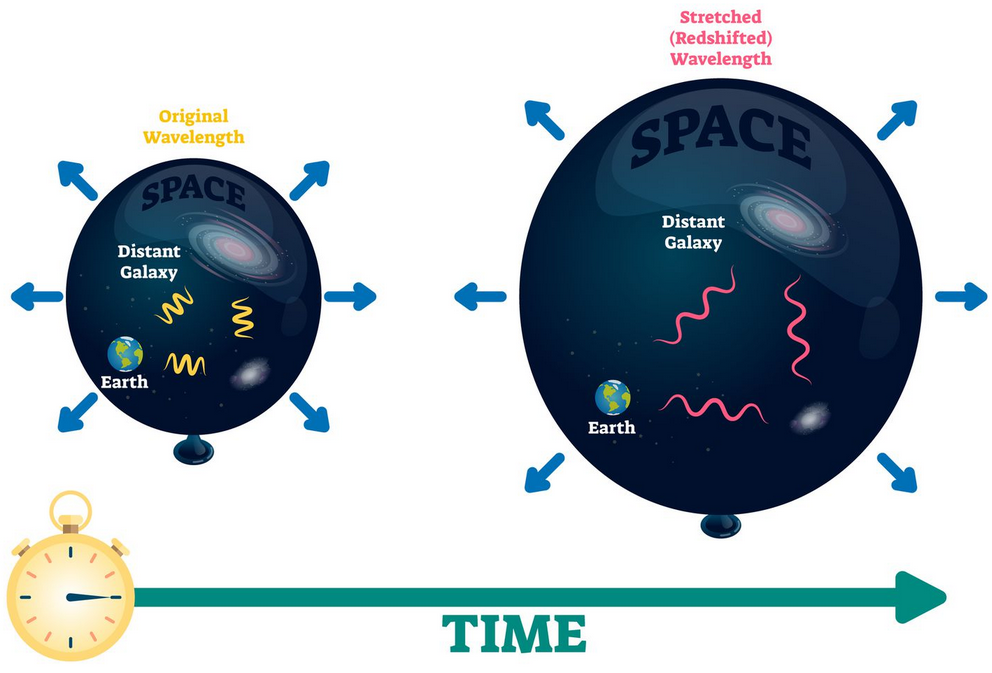
- This shift is observed in the spectral lines of stars and galaxies.
Example
A train sounding a whistle of \( \mathrm{800 \ Hz} \) passes a stationary observer. The observer hears a higher frequency as the train approaches and a lower frequency as it departs. Explain why.
▶️ Answer / Explanation
As the train approaches, the wavefronts are compressed, so wavelength decreases and frequency increases (higher pitch). As the train moves away, wavefronts are stretched, so wavelength increases and frequency decreases (lower pitch). This is the Doppler effect for sound.
Example
Light from a galaxy is observed to have its spectral lines shifted toward the red. What does this indicate about the motion of the galaxy relative to Earth?
▶️ Answer / Explanation
Redshift means the observed wavelength is longer (frequency lower). This occurs when the source (galaxy) is moving away from the observer (Earth). Hence, the galaxy is receding — evidence for the expansion of the universe.
2. Representation of the Doppler Effect using Wavefront Diagrams
The wavefront diagram representation of the Doppler effect shows how the spacing and direction of wavefronts change when either the source or the observer is in motion relative to the medium. It provides a visual understanding of how frequency and wavelength appear different to a moving observer or from a moving source.
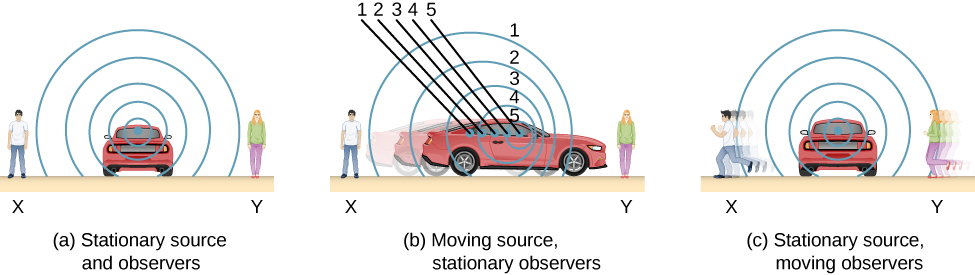
Stationary Source:
- When the source is stationary, wavefronts spread out symmetrically in all directions.
- The wavelength and frequency are the same in every direction.
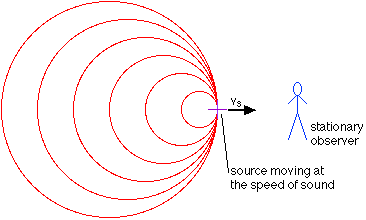
Moving Source:
- When the source moves, wavefronts in the direction of motion become closer together (shorter wavelength), and wavefronts behind become more spread out (longer wavelength).
- This results in a higher frequency observed ahead of the source and a lower frequency behind.
- The Doppler effect becomes more pronounced as the source’s speed increases relative to the wave speed.
Moving Observer:
- If the observer moves toward the source, they encounter wavefronts more frequently — observed frequency increases.
- If the observer moves away, they encounter fewer wavefronts per second — observed frequency decreases.
- The wave speed relative to the observer changes, even though the wavefront spacing remains the same in the medium.
Mathematical Relationships (for Sound Waves):
\(\mathrm{f’ = f \left(\dfrac{v \pm u_o}{v}\right)}\) (moving observer)
\(\mathrm{f’ = f \left(\dfrac{v}{v \mp u_s}\right)}\) (moving source)
- \( \mathrm{f’} \) = observed frequency
- \( \mathrm{f} \) = source frequency
- \( \mathrm{v} \) = speed of wave in medium
- \( \mathrm{u_o} \) = speed of observer
- \( \mathrm{u_s} \) = speed of source
- Sign convention: use + when moving toward, − when moving away
Example
Draw or describe the wavefront pattern for a sound source moving at a constant speed less than the speed of sound. Explain why the observer in front hears a higher pitch.
▶️ Answer / Explanation
When the source moves forward, it emits successive wavefronts closer together in front and farther apart behind.

An observer in front experiences a higher frequency (shorter wavelength, higher pitch), while one behind hears a lower frequency (longer wavelength, lower pitch). The compression of wavefronts ahead causes the increased pitch.
Example
A sound source moves at \( \mathrm{30 \ m/s} \) emitting a tone of \( \mathrm{500 \ Hz} \). If the speed of sound is \( \mathrm{340 \ m/s} \), calculate the frequency heard by an observer directly in front of the source.
▶️ Answer / Explanation
Given: \( \mathrm{f = 500 \ Hz}, \ \mathrm{v = 340 \ m/s}, \ \mathrm{u_s = 30 \ m/s} \)
For a moving source (observer stationary): \( \mathrm{f’ = f \left( \dfrac{v}{v – u_s} \right)} \)
\( \mathrm{f’ = 500 \left( \dfrac{340}{340 – 30} \right) = 500 \left( \dfrac{340}{310} \right) = 500(1.097) = 548.5 \ Hz.} \)
Therefore, the observer hears a frequency of approximately \( \mathrm{549 \ Hz.} \)
3. The Relative Change in Frequency or Wavelength Observed for a Light Wave Due to the Doppler Effect (Low-Speed Approximation)
For electromagnetic waves (light), the Doppler effect occurs as a change in the observed frequency or wavelength when there is relative motion between the source and the observer. At low speeds (when \( \mathrm{v \ll c} \)), this change can be described by a simple approximate relationship between the fractional frequency or wavelength change and the relative velocity.
Mathematical Expression:
\( \mathrm{\dfrac{\Delta f}{f} = \dfrac{\Delta \lambda}{\lambda} \approx \dfrac{v}{c}} \)
- \( \mathrm{\Delta f} \) = change in frequency
- \( \mathrm{f} \) = original (emitted) frequency
- \( \mathrm{\Delta \lambda} \) = change in wavelength
- \( \mathrm{\lambda} \) = emitted wavelength
- \( \mathrm{v} \) = relative velocity between source and observer
- \( \mathrm{c} \) = speed of light in vacuum (\( \mathrm{3.0 \times 10^8 \ m/s} \))
Interpretation:
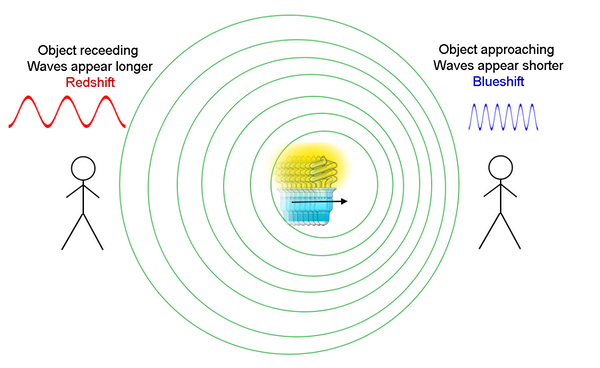
- If the source moves toward the observer → \( \mathrm{v} \) is negative → \( \mathrm{\lambda’} < \lambda \) → higher observed frequency (blueshift).
- If the source moves away from the observer → \( \mathrm{v} \) is positive → \( \mathrm{\lambda’} > \lambda \) → lower observed frequency (redshift).
Example
Light from a star has a rest wavelength of \( \mathrm{600 \ nm.} \) It is observed at \( \mathrm{602 \ nm.} \) Estimate the speed of the star relative to Earth. Assume \( \mathrm{v \ll c.} \)
▶️ Answer / Explanation
Given: \( \mathrm{\lambda = 600 \ nm, \ \lambda’ = 602 \ nm, \ c = 3.0 \times 10^8 \ m/s} \)
Change in wavelength: \( \mathrm{\Delta \lambda = 2 \ nm} \)
Using \( \mathrm{\dfrac{\Delta \lambda}{\lambda} = \dfrac{v}{c}} \):
\( \mathrm{v = c \dfrac{\Delta \lambda}{\lambda} = 3.0 \times 10^8 \times \dfrac{2}{600} \times 10^{-9}/10^{-9} = 1.0 \times 10^6 \ m/s.} \)
Since wavelength increased (redshift), the star is moving away from Earth.
Speed = \( \mathrm{1.0 \times 10^6 \ m/s.} \)
Example
A spectral line of hydrogen normally at \( \mathrm{486.1 \ nm} \) is observed in the light from a distant galaxy at \( \mathrm{490.0 \ nm.} \) Calculate the recession velocity of the galaxy, assuming \( \mathrm{v \ll c.} \)
▶️ Answer / Explanation
Given: \( \mathrm{\lambda = 486.1 \ nm, \ \lambda’ = 490.0 \ nm, \ c = 3.0 \times 10^8 \ m/s.} \)
\( \mathrm{\Delta \lambda = 490.0 – 486.1 = 3.9 \ nm.} \)
Using \( \mathrm{\dfrac{\Delta \lambda}{\lambda} = \dfrac{v}{c}} \):
\( \mathrm{v = c \dfrac{3.9}{486.1} \times 10^{-9}/10^{-9} = 3.0 \times 10^8 \times 0.00802 = 2.41 \times 10^6 \ m/s.} \)
The galaxy is receding from Earth at \( \mathrm{2.4 \times 10^6 \ m/s.} \)
4. Shifts in Spectral Lines and Motion of Celestial Bodies
The Doppler shift of light causes the observed spectral lines of a moving celestial object to appear at different wavelengths than when measured in the laboratory. By measuring this shift, astronomers can determine whether a star or galaxy is moving toward or away from Earth and calculate its radial velocity (speed along the line of sight).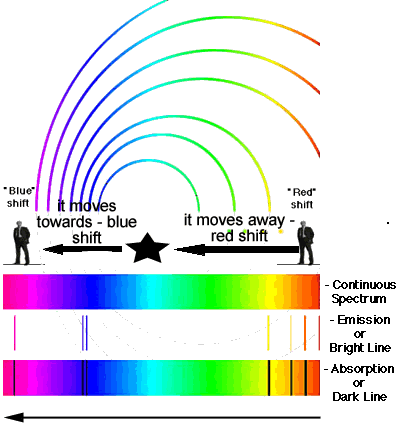
Spectral Line Observation:
- Each element emits or absorbs light at specific characteristic wavelengths (its spectral fingerprint).
- If the observed spectral lines are shifted compared to their laboratory wavelengths, it indicates relative motion.
- This shift can be measured with great precision using spectroscopic instruments.
Types of Shifts:
- Redshift: Spectral lines move toward longer wavelengths → object moving away from observer.
- Blueshift: Spectral lines move toward shorter wavelengths → object moving toward observer.
Quantitative Relationship:
\( \mathrm{\dfrac{\Delta \lambda}{\lambda} = \dfrac{v}{c}} \)
- \( \mathrm{\Delta \lambda = \lambda_{observed} – \lambda_{rest}} \)

- \( \mathrm{v} \) = velocity of the object relative to the observer (positive for receding, negative for approaching)
- \( \mathrm{c} \) = speed of light (\( \mathrm{3.0 \times 10^8 \ m/s} \))
Key Applications in Astronomy:
- Determining the radial velocities of stars, galaxies, and exoplanets.
- Measuring the rotation speeds of galaxies (spectral lines broaden due to rotation).
- Providing evidence for the expansion of the universe (galaxies show redshifts proportional to their distance — Hubble’s Law).

Example
The hydrogen line that normally occurs at \( \mathrm{656.3 \ nm} \) is observed in the light from a distant galaxy at \( \mathrm{660.3 \ nm.} \) What does this tell us about the galaxy’s motion?
▶️ Answer / Explanation
The wavelength has increased (redshift), meaning the galaxy is moving away from Earth. The shift toward longer wavelengths indicates a receding motion.
Example
Light from a distant quasar shows a spectral line normally at \( \mathrm{434.0 \ nm} \), now observed at \( \mathrm{456.0 \ nm.} \) Calculate the quasar’s speed relative to Earth. Assume \( \mathrm{v \ll c.} \)
▶️ Answer / Explanation
Given: \( \mathrm{\lambda_{rest} = 434.0 \ nm, \ \lambda_{obs} = 456.0 \ nm, \ c = 3.0 \times 10^8 \ m/s.} \)
Change in wavelength: \( \mathrm{\Delta \lambda = 22.0 \ nm.} \)
Using \( \mathrm{\dfrac{\Delta \lambda}{\lambda} = \dfrac{v}{c}} \):
\( \mathrm{v = c \dfrac{\Delta \lambda}{\lambda} = 3.0 \times 10^8 \times \dfrac{22}{434} \times 10^{-9}/10^{-9} = 3.0 \times 10^8 \times 0.0507 = 1.52 \times 10^7 \ m/s.} \)
Therefore, the quasar is moving away from Earth at approximately \( \mathrm{1.5 \times 10^7 \ m/s.} \)