Download IITian Academy App for accessing Online Mock Tests and More..
Question
The group \(\left\{ {G,\left. * \right\}} \right.\) is defined on the set \(G = \left\{ {1,2,3,4,5,\left. 6 \right\}} \right.\) where \( * \) denotes multiplication modulo \(7\).
Draw the Cayley table for \(\left\{ {G,\left. * \right\}} \right.\) .
(i) Determine the order of each element of \(\left\{ {G,\left. * \right\}} \right.\) .
(ii) Find all the proper subgroups of \(\left\{ {G,\left. * \right\}} \right.\) .
Solve the equation \(x * 6 * x = 3\) where \(x \in G\) .
Answer/Explanation
Markscheme
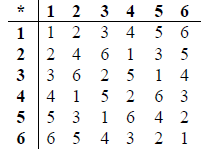A3
Note: Award A2 for 1 error, A1 for 2 errors, A0 for 3 or more errors.
[3 marks]
(i) We first identify \(1\) as the identity (A1)
Order of \(1 = 1\)
Order of \(2 = 3\)
Order of \(3 = 6\)
Order of \(4 = 3\)
Order of \(5 = 6\)
Order of \(6 = 2\) A3
Note: Award A2 for 1 error, A1 for 2 errors, A0 for more than 2 errors.
(ii) \(\left\{ {1,\left. 6 \right\}} \right.\) ; \(\left\{ {1,\left. {2,4} \right\}} \right.\) A1A1
[6 marks]
The equation is equivalent to
\(6 * x * x = 3\) M1
\(x * x = 4\)
\(x = 2\) or \(5\) A1A1
[3 marks]
Question
\(\{ G,{\text{ }} * \} \) is a group of order \(N\) and \(\{ H,{\text{ }} * \} \) is a proper subgroup of \(\{ G,{\text{ }} * \} \) of order \(n\).
(a) Define the right coset of \(\{ H,{\text{ }} * \} \) containing the element \(a \in G\).
(b) Show that each right coset of \(\{ H,{\text{ }} * \} \) contains \(n\) elements.
(c) Show that the union of the right cosets of \(\{ H,{\text{ }} * \} \) is equal to \(G\).
(d) Show that any two right cosets of \(\{ H,{\text{ }} * \} \) are either equal or disjoint.
(e) Give a reason why the above results can be used to prove that \(N\) is a multiple of \(n\).
Answer/Explanation
Markscheme
(a) the right coset containing \(a\) has the form \(\{ ha|h \in H\} \) A1
[1 mark]
Note: From here on condone the use of left cosets.
(b) let \(b\), \(c\) be distinct elements of \(H\). Then, given \(a \in G\), by the Latin square property of the Cayley table, \(ba\) and \(ca\) are distinct A1
therefore each element of \(H\) corresponds to a unique element in the coset which must therefore contain \(n\) elements R1
[2 marks]
(c) let \(d\) be any element of \(G\). Then since \(H\) contains the identity \(e\), \(ed = d\) will be in a coset R1
therefore every element of \(G\) will be contained in a coset which proves that the union of all the cosets is \(G\) R1
[2 marks]
(d) let the cosets of \(b\) and \(c{\text{ }}(b,{\text{ }}c \in G)\) contain a common element so that
\(pb = qc\) where \(p,{\text{ }}q \in H\). Let \(r\) denote any other element \( \in H\) M1
then
\(rb = r{p^{ – 1}}qc\) A1
since \(r{p^{ – 1}}q \in H\), this shows that all the other elements are common and the cosets are equal R1
since not all cosets can be equal, there must be other cosets which are disjoint R1
[4 marks]
(e) the above results show that \(G\) is partitioned into a number of disjoint subsets containing \(n\) elements so that \(N\) must be a multiple of \(n\) R1
[1 mark]