Question 11. [Maximum mark: 7]
The diagram below shows a network of roads in a small village with the weights indicating the distance of each road, in metres, and junctions indicated with letters.
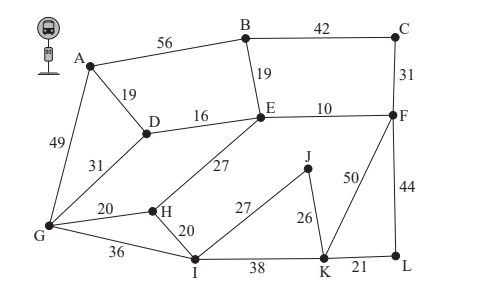
Musab is required to deliver leaflets to every house on each road. He wishes to minimize his total distance. Musab starts and finishes from the village bus-stop at A.
a. Determine the total distance Musab will need to walk. [5]
Instead of having to catch the bus to the village, Musab’s sister offers to drop him off at any junction and pick him up at any other junction of his choice.
b. Explain which junctions Musab should choose as his starting and finishing points. [2]
▶️Answer/Explanation
(a) Odd vertices are A, B, D, H Consider pairings.
AB DH has shortest route AD, DE, EB and DE, EH,
so repeated edges \( ( 19 + 16 + 19) + 16 + 27 = 9 7 \)
AD BH has shortest route AD and BE, EH, so repeated edges \(19+ (19+ 27) = 65 \)
AH BD has shortest route AD, DE, EH and BE, ED, so repeated edges \((19 + 16 + 27) +(19 + 16) = 97 \)
so best pairing is AD, BH weight of route is therefore \(582 + 65 = 647\)
(b) least value of the pairings is 19 therefore repeat AD B and H
Question 10. [Maximum mark: 7]
An engineer plans to visit six oil rigs (A–F) in the Gulf of Mexico, starting and finishing at A. The travelling time, in minutes, between each of the rigs is shown in the table.
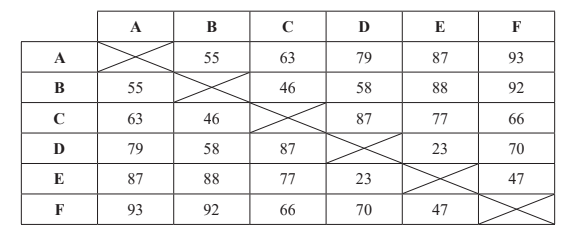
(a) (i) Use Prim’s algorithm to find the weight of the minimum spanning tree of the subgraph of G obtained by deleting A and starting at B. List the order in which the edges are selected.The data above can be represented by a graph G .
(ii) Hence find a lower bound for the travelling time needed to visit all the oil rigs. [6]
(b) Describe how an improved lower bound might be found. [1]
▶️Answer/Explanation
(a) (i) use of Prim’s algorithm BC 46 BD 58 DE 23 EF 47 Total 174 (ii) AB+ AC = 55 + 63 = 118 174 + 118 = 292 minutes (b) delete a different vertex
Question
A modern art painting is contained in a square frame. The painting has a shaded region
bounded by a smooth curve and a horizontal line.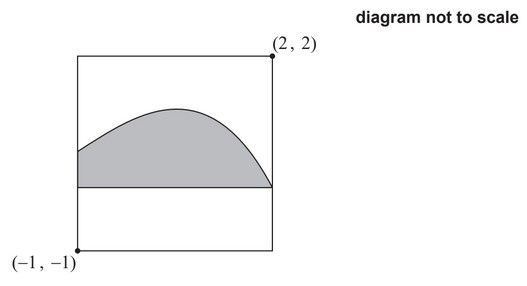
When the painting is placed on a coordinate axes such that the bottom left corner of the
painting has coordinates (−1, −1) and the top right corner has coordinates (2 , 2), the
curve can be modelled by y = f (x) and the horizontal line can be modelled by the x-axis.
Distances are measured in metres.
(a) Use the trapezoidal rule, with the values given in the following table, to approximate
the area of the shaded region.
| x | -1 | 0 | 1 | 2 |
| y | 0.6 | 1.2 | 1.2 | 0 |
The artist used the equation \(y=\frac{-x^3-3x^2+4x+12}{10}\) to draw the curve.
(b) Find the exact area of the shaded region in the painting.
(c) Find the area of the unshaded region in the painting.
▶️Answer/Explanation
Ans:
(a) \(\frac{1}{2}(0.6+0+2(1.2 + 1.2))\)
2.7 \(m^2\)
(b) \(\int_{-1}^{2}\frac{-x^3-3x^2+4x+12}{10}\) OR \(\int_{-1}^{2}f(x)dx\)
2.925 \(m^2\)
(c) 9-2.925
= 6.08 \(m^2\) (6.075)
Question

The above diagram shows the weighted graph \(G\).
a.Determine whether or not \(G\) is bipartite.[2]
b.(i) Write down the adjacency matrix for \(G\).
(ii) Find the number of distinct walks of length \(4\) beginning and ending at A.[4]
▶️Answer/Explanation
Markscheme
\(G\) is bipartite A1
because it contains a triangle. R1
Note: Award R1 for a valid attempt at showing that the vertices cannot be divided into two disjoint sets.
[2 marks]
(i)
\({\boldsymbol{M}} = \left( {\begin{array}{*{20}{c}}
0&1&0&0&0&1 \\
1&0&1&1&1&0 \\
0&1&0&1&0&0 \\
0&1&1&0&1&1 \\
0&1&0&1&0&1 \\
1&0&0&1&1&0
\end{array}} \right)\) A1
(ii) We require the (A, A) element of \({\boldsymbol{M}^4}\) which is \(13\). M1A2
[4 marks]
Question
The figure below shows the graph G .
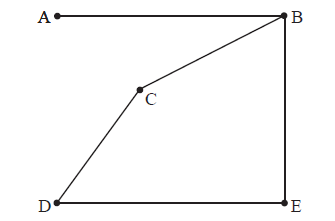
(ii) Find the number of walks of length \(4\) beginning and ending at B.[5]
(ii) Write down the degrees of all the vertices of \(G\) and all the vertices of \(G’\).
(iii) Hence, or otherwise, determine whether or not \(G\) and \(G’\) are isomorphic.[6]
▶️Answer/Explanation
Markscheme
(i) the adjacency matrix is
\(\left( {\begin{array}{*{20}{c}}
0&1&0&0&0\\
1&0&1&0&1\\
0&1&0&1&0\\
0&0&1&0&1\\
0&1&0&1&0
\end{array}} \right)\) A2
Note: Award A2 for correct matrix, A1 for one or two errors and A0 for more than two errors.
(ii) the required number of walks is the (B, B) element in the fourth power of the adjacency matrix (M1)
using a GDC gives the answer as 13 A2
[5 marks]
(i)
A2
(ii)
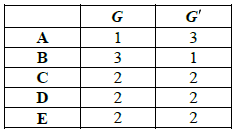 A1A1
A1A1
(iii) In \(G\), the vertex of degree 1 is adjacent to the vertex of degree 3, whereas in \(G’\) the vertex of degree \(1\) is adjacent to a vertex of degree \(2\). They are not therefore isomorphic. A1R1
Note: Accept alternative correct solutions.
[6 marks]
