Question
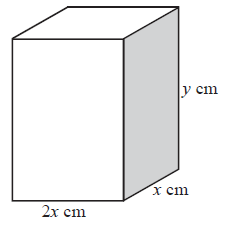
A closed rectangular box has a height \(y{\text{ cm}}\) and width \(x{\text{ cm}}\). Its length is twice its width. It has a fixed outer surface area of \(300{\text{ c}}{{\text{m}}^2}\) .
Factorise \(3{x^2} + 13x – 10\).[2]
Solve the equation \(3{x^2} + 13x – 10 = 0\).[2]
Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Find the equation of the axis of symmetry on the graph of this function.[2]
Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Calculate the minimum value of this function.[2]
Show that \(4{x^2} + 6xy = 300\).[2]
Find an expression for \(y\) in terms of \(x\).[2]
Hence show that the volume \(V\) of the box is given by \(V = 100x – \frac{4}{3}{x^3}\).[2]
Find \(\frac{{{\text{d}}V}}{{{\text{d}}x}}\).[2]
(i) Hence find the value of \(x\) and of \(y\) required to make the volume of the box a maximum.
(ii) Calculate the maximum volume.[5]
Answer/Explanation
Markscheme
\((3x – 2)(x + 5)\) (A1)(A1)[2 marks]
\((3x – 2)(x + 5) = 0\)
\(x = \frac{2}{3}\) or \(x = – 5\) (A1)(ft)(A1)(ft)(G2)[2 marks]
\(x = \frac{{ – 13}}{6}{\text{ }}( – 2.17)\) (A1)(A1)(ft)(G2)
Note: (A1) is for \(x = \), (A1) for value. (ft) if value is half way between roots in (b).[2 marks]
Minimum \(y = 3{\left( {\frac{{ – 13}}{6}} \right)^2} + 13\left( {\frac{{ – 13}}{6}} \right) – 10\) (M1)
Note: (M1) for substituting their value of \(x\) from (c) into \(f(x)\) .
\( = – 24.1\) (A1)(ft)(G2)[2 marks]
\({\text{Area}} = 2(2x)x + 2xy + 2(2x)y\) (M1)(A1)
Note: (M1) for using the correct surface area formula (which can be implied if numbers in the correct place). (A1) for using correct numbers.
\(300 = 4{x^2} + 6xy\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(6xy = 300 – 4{x^2}\) (M1)
\(y = \frac{{300 – 4{x^2}}}{{6x}}\) or \(\frac{{150 – 2{x^2}}}{{3x}}\) (A1)[2 marks]
\({\text{Volume}} = x(2x)y\) (M1)
\(V = 2{x^2}\left( {\frac{{300 – 4{x^2}}}{{6x}}} \right)\) (A1)(ft)
\( = 100x – \frac{4}{3}{x^3}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 100 – \frac{{12{x^2}}}{3}\) or \(100 – 4{x^2}\) (A1)(A1)
Note: (A1) for each term.[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column
(i) For maximum \(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) or \(100 – 4{x^2} = 0\) (M1)
\(x = 5\) (A1)(ft)
\(y = \frac{{300 – 4{{(5)}^2}}}{{6(5)}}\) or \(\left( {\frac{{150 – 2{{(5)}^2}}}{{3(5)}}} \right)\) (M1)
\( = \frac{{20}}{3}\) (A1)(ft)
(UP) (ii) \(333\frac{1}{3}{\text{ c}}{{\text{m}}^3}{\text{ }}(333{\text{ c}}{{\text{m}}^3})\)
Note: (ft) from their (e)(i) if working for volume is seen.[5 marks]
Question
A geometric sequence has \(1024\) as its first term and \(128\) as its fourth term.
Consider the arithmetic sequence \(1{\text{, }}4{\text{, }}7{\text{, }}10{\text{, }}13{\text{, }} \ldots \)
Show that the common ratio is \(\frac{1}{2}\) .[2]
Find the value of the eleventh term.[2]
Find the sum of the first eight terms.[3]
Find the number of terms in the sequence for which the sum first exceeds \(2047.968\).[3]
Find the value of the eleventh term.[2]
The sum of the first \(n\) terms of this sequence is \(\frac{n}{2}(3n – 1)\).
(i) Find the sum of the first 100 terms in this arithmetic sequence.
(ii) The sum of the first \(n\) terms is \(477\).
(a) Show that \(3{n^2} – n – 954 = 0\) .
(b) Using your graphic display calculator or otherwise, find the number of terms, \(n\) .[6]
Answer/Explanation
Markscheme
\(1024{r^3} = 128\) (M1)
\({r^3} = \frac{1}{8}\) or \(r = \sqrt[3]{{\frac{1}{8}}}\) (M1)
\(r = \frac{1}{2}{\text{ }}(0.5)\) (AG)
Notes: Award at most (M1)(M0) if last line not seen. Award (M1)(M0) if \(128\) is found by repeated multiplication (division) of \(1024\) by \(0.5\) \((2)\).[2 marks]
\(1024 \times {0.5^{10}}\) (M1)
Notes: Award (M1) for correct substitution into correct formula. Accept an equivalent method.
1 (A1)(G2)[2 marks]
\({S_8} = \frac{{1024\left( {1 – {{\left( {\frac{1}{2}} \right)}^8}} \right)}}{{1 – \frac{1}{2}}}\) (M1)(A1)
Note: Award (M1) for substitution into the correct formula, (A1) for correct substitution.
OR
(A1) for complete and correct list of eight terms (A1)
(M1) for their eight terms added (M1)
\({S_8} = 2040\) (A1)(G2)[3 marks]
\(\frac{{1024\left( {1 – {{\left( {\frac{1}{2}} \right)}^n}} \right)}}{{1 – \frac{1}{2}}} > 2047.968\) (M1)(M1)(ft)
Notes: Award (M1) for correct substitution into the correct formula for the sum, (M1) for comparing to \(2047.968\) . Accept equation. Follow through from their expression for the sum used in part (c).
OR
If a list is used: \({S_{15}} = 2047.9375\) (M1)
\({S_{16}} = 2047.96875\) (M1)
\(n = 16\) (A1)(ft)(G2)
Note: Follow through from their expression for the sum used in part (c).[3 marks]
\({\text{common difference}} = 3\) (may be implied) (A1)
\({u_{11}} = 31\) (A1)(G2)[2 marks]
(i) \(\frac{{100}}{2}(3 \times 100 – 1)\) OR \(\frac{{100(2 + 99 \times 3)}}{2}\) (M1)
\(14 950\) (A1)(G2)
(ii) (a) \(\frac{n}{2}(3n – 1) = 477\) OR \(\frac{n}{2}(2 + 3(n – 1)) = 477\) (M1)
\(3{n^2} – n = 954\) (M1)
\(3{n^2} – n – 954 = 0\) (AG)
Notes: Award second (M1) for correct removal of denominator or brackets and no further incorrect working seen. Award at most
(M1)(M0) if last line not seen.
(b) \(18\) (G2)
Note: If both solutions to the quadratic equation are seen and the correct value is not identified as the required answer, award (G1)(G0).[6 marks]
Question
A lobster trap is made in the shape of half a cylinder. It is constructed from a steel frame with netting pulled tightly around it. The steel frame consists of a rectangular base, two semicircular ends and two further support rods, as shown in the following diagram.
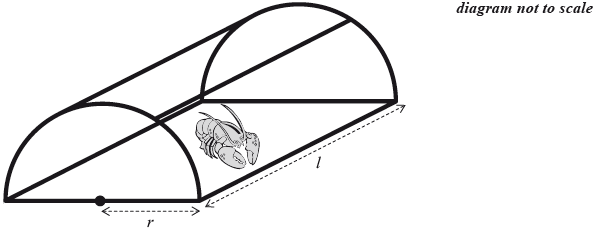
The semicircular ends each have radius \(r\) and the support rods each have length \(l\).
Let \(T\) be the total length of steel used in the frame of the lobster trap.
Write down an expression for \(T\) in terms of \(r\), \(l\) and \(\pi \).[3]
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Write down an equation for the volume of the lobster trap in terms of \(r\), \(l\) and \(\pi \).[3]
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Show that \(T = (2\pi + 4)r + \frac{6}{{\pi {r^2}}}\).[2]
The volume of the lobster trap is \(0.75{\text{ }}{{\text{m}}^{\text{3}}}\).
Find \(\frac{{{\text{d}}T}}{{{\text{d}}r}}\).[3]
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Show that the value of \(r\) for which \(T\) is a minimum is \(0.719 {\text{ m}}\), correct to three significant figures.[2]
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Calculate the value of \(l\) for which \(T\) is a minimum.[2]
The lobster trap is designed so that the length of steel used in its frame is a minimum.
Calculate the minimum value of \(T\).[2]
Answer/Explanation
Markscheme
\(2\pi r + 4r + 4l\) (A1)(A1)(A1)
Notes: Award (A1) for \(2\pi r\) (“\(\pi \)” must be seen), (A1) for \(4r\), (A1) for \(4l\). Accept equivalent forms. Accept \(T = 2\pi r + 4r + 4l\). Award a maximum of (A1)(A1)(A0) if extra terms are seen.[3 marks]
\(0.75 = \frac{{\pi {r^2}l}}{2}\) (A1)(A1)(A1)
Notes: Award (A1) for their formula equated to \(0.75\), (A1) for \(l\) substituted into volume of cylinder formula, (A1) for volume of cylinder formula divided by \(2\).
If “\(\pi \)” not seen in part (a) accept use of \(3.14\) or greater accuracy. Award a maximum of (A1)(A1)(A0) if extra terms are seen.[3 marks]
\(T = 2\pi r + 4r + 4\left( {\frac{{1.5}}{{\pi {r^2}}}} \right)\) (A1)(ft)(A1)
\( = (2\pi + 4)r + \frac{6}{{\pi {r^2}}}\) (AG)
Notes: Award (A1)(ft) for correct rearrangement of their volume formula in part (b) seen, award (A1) for the correct substituted formula for \(T\). The final line must be seen, with no incorrect working, for this second (A1) to be awarded.[2 marks]
\(\frac{{{\text{d}}T}}{{{\text{d}}r}} = 2\pi + 4 – \frac{{12}}{{\pi {r^3}}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi + 4\), (A1) for \(\frac{{ – 12}}{\pi }\), (A1) for \({r^{ – 3}}\).
Accept 10.3 (10.2832…) for \(2\pi + 4\), accept \(–3.82\) \(–3.81971…\) for \(\frac{{ – 12}}{\pi }\). Award a maximum of (A1)(A1)(A0) if extra terms are seen.[3 marks]
\(2\pi + 4 – \frac{{12}}{{\pi {r^3}}} = 0\) OR \(\frac{{{\text{d}}T}}{{{\text{d}}r}} = 0\) (M1)
Note: Award (M1) for setting their derivative equal to zero.
\(r = 0.718843 \ldots \) OR \(\sqrt[3]{{0.371452 \ldots }}\) OR \(\sqrt[3]{{\frac{{12}}{{\pi (2\pi + 4)}}}}\) OR \(\sqrt[3]{{\frac{{3.81971}}{{10.2832 \ldots }}}}\) (A1)
\(r = 0.719{\text{ (m)}}\) (AG)
Note: The rounded and unrounded or formulaic answers must be seen for the final (A1) to be awarded. The use of \(3.14\) gives an unrounded answer of \(r = 0.719039 \ldots \).[2 marks]
\(0.75 = \frac{{\pi \times {{(0.719)}^2}l}}{2}\) (M1)
Note: Award (M1) for substituting \(0.719\) into their volume formula. Follow through from part (b).
\(l = 0.924{\text{ (m)}}\) \((0.923599 \ldots )\) (A1)(ft)(G2)[2 marks]
\(T = (2\pi + 4) \times 0.719 + \frac{6}{{\pi {{(0.719)}^2}}}\) (M1)
Notes: Award (M1) for substituting \(0.719\) in their expression for \(T\). Accept alternative methods, for example substitution of their \(l\) and \(0.719\) into their part (a) (for which the answer is \(11.08961024\)). Follow through from their answer to part (a).
\( = 11.1{\text{ (m)}}\) \((11.0880 \ldots )\) (A1)(ft)(G2)
Question
A parcel is in the shape of a rectangular prism, as shown in the diagram. It has a length \(l\) cm, width \(w\) cm and height of \(20\) cm.
The total volume of the parcel is \(3000{\text{ c}}{{\text{m}}^3}\).
Express the volume of the parcel in terms of \(l\) and \(w\).[1]
Show that \(l = \frac{{150}}{w}\).[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
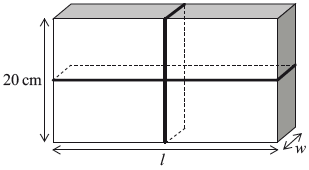
Show that the length of string, \(S\) cm, required to tie up the parcel can be written as
\[S = 40 + 4w + \frac{{300}}{w},{\text{ }}0 < w \leqslant 20.\][2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Draw the graph of \(S\) for \(0 < w \leqslant 20\) and \(0 < S \leqslant 500\), clearly showing the local minimum point. Use a scale of \(2\) cm to represent \(5\) units on the horizontal axis \(w\) (cm), and a scale of \(2\) cm to represent \(100\) units on the vertical axis \(S\) (cm).[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find \(\frac{{{\text{d}}S}}{{{\text{d}}w}}\).[3]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find the value of \(w\) for which \(S\) is a minimum.[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Write down the value, \(l\), of the parcel for which the length of string is a minimum.[1]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find the minimum length of string required to tie up the parcel.[2]
Answer/Explanation
Markscheme
\(20lw\) OR \(V = 20lw\) (A1)[1 mark]
\(3000 = 20lw\) (M1)
Note: Award (M1) for equating their answer to part (a) to \(3000\).
\(l = \frac{{3000}}{{20w}}\) (M1)
Note: Award (M1) for rearranging equation to make \(l\) subject of the formula. The above equation must be seen to award (M1).
OR
\(150 = lw\) (M1)
Note: Award (M1) for division by \(20\) on both sides. The above equation must be seen to award (M1).
\(l = \frac{{150}}{w}\) (AG)[2 marks]
\(S = 2l + 4w + 2(20)\) (M1)
Note: Award (M1) for setting up a correct expression for \(S\).
\(2\left( {\frac{{150}}{w}} \right) + 4w + 2(20)\) (M1)
Notes: Award (M1) for correct substitution into the expression for \(S\). The above expression must be seen to award (M1).
\( = 40 + 4w + \frac{{300}}{w}\) (AG)[2 marks]
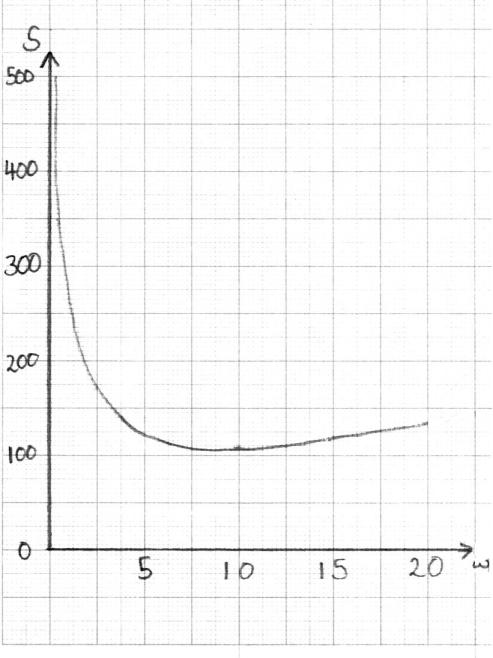(A1)(A1)(A1)(A1)
Note: Award (A1) for correct scales, window and labels on axes, (A1) for approximately correct shape, (A1) for minimum point in approximately correct position, (A1) for asymptotic behaviour at \(w = 0\).
Axes must be drawn with a ruler and labeled \(w\) and \(S\).
For a smooth curve (with approximately correct shape) there should be one continuous thin line, no part of which is straight and no (one-to-many) mappings of \(w\).
The \(S\)-axis must be an asymptote. The curve must not touch the \(S\)-axis nor must the curve approach the asymptote then deviate away later.[4 marks]
\(4 – \frac{{300}}{{{w^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(4\), (A1) for \(-300\), (A1) for \(\frac{1}{{{w^2}}}\) or \({w^{ – 2}}\). If extra terms present, award at most (A1)(A1)(A0).[3 marks]
\(4 – \frac{{300}}{{{w^2}}} = 0\) OR \(\frac{{300}}{{{w^2}}} = 4\) OR \(\frac{{{\text{d}}S}}{{{\text{d}}w}} = 0\) (M1)
Note: Award (M1) for equating their derivative to zero.
\(w = 8.66{\text{ }}\left( {\sqrt {75} ,{\text{ 8.66025}} \ldots } \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (e).[2 marks]
\(17.3 \left( {\frac{{150}}{{\sqrt {75} }},{\text{ 17.3205}} \ldots } \right)\) (A1)(ft)
Note: Follow through from their answer to part (f).[1 mark]
\(40 + 4\sqrt {75} + \frac{{300}}{{\sqrt {75} }}\) (M1)
Note: Award (M1) for substitution of their answer to part (f) into the expression for \(S\).
\( = 110{\text{ (cm) }}\left( {40 + 40\sqrt 3 ,{\text{ 109.282}} \ldots } \right)\) (A1)(ft)(G2)
Note: Do not accept \(109\).
Follow through from their answers to parts (f) and (g).[2 marks]
Question
Tepees were traditionally used by nomadic tribes who lived on the Great Plains of North America. They are cone-shaped dwellings and can be modelled as a cone, with vertex O, shown below. The cone has radius, \(r\), height, \(h\), and slant height, \(l\).
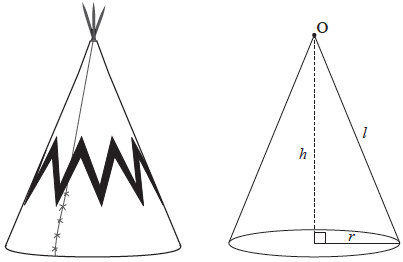
A model tepee is displayed at a Great Plains exhibition. The curved surface area of this tepee is covered by a piece of canvas that is \(39.27{\text{ }}{{\text{m}}^2}\), and has the shape of a semicircle, as shown in the following diagram.
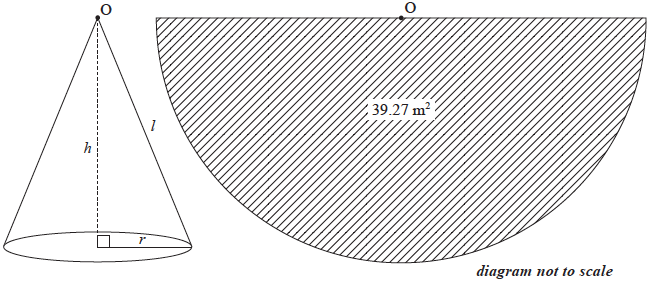
Show that the slant height, \(l\), is \(5\) m, correct to the nearest metre.[2]
(i) Find the circumference of the base of the cone.
(ii) Find the radius, \(r\), of the base.
(iii) Find the height, \(h\).[6]
A company designs cone-shaped tents to resemble the traditional tepees.
These cone-shaped tents come in a range of sizes such that the sum of the diameter and the height is equal to 9.33 m.
Write down an expression for the height, \(h\), in terms of the radius, \(r\), of these cone-shaped tents.[1]
A company designs cone-shaped tents to resemble the traditional tepees.
These cone-shaped tents come in a range of sizes such that the sum of the diameter and the height is equal to 9.33 m.
Show that the volume of the tent, \(V\), can be written as
\[V = 3.11\pi {r^2} – \frac{2}{3}\pi {r^3}.\][1]
A company designs cone-shaped tents to resemble the traditional tepees.
These cone-shaped tents come in a range of sizes such that the sum of the diameter and the height is equal to 9.33 m.
Find \(\frac{{{\text{d}}V}}{{{\text{d}}r}}\).[2]
A company designs cone-shaped tents to resemble the traditional tepees.
These cone-shaped tents come in a range of sizes such that the sum of the diameter and the height is equal to 9.33 m.
(i) Determine the exact value of \(r\) for which the volume is a maximum.
(ii) Find the maximum volume.[4]
Answer/Explanation
Markscheme
\(\frac{{\pi {l^2}}}{2} = 39.27\) (M1)(A1)
Note: Award (M1) for equating the formula for area of a semicircle to \(39.27\), award (A1) for correct substitution of \(l\) into the formula for area of a semicircle.
\(l = 5{\text{ (m)}}\) (AG)
(i) \(5 \times \pi \) (M1)
\( = 15.7\;\;\;(15.7079…,{\text{ }}5\pi )\;{\text{(m)}}\) (A1)(G2)
(ii) \(2\pi r = 15.7079…\;\;\;\)OR\(\;\;\;5\pi r = 39.27\) (M1)
\((r = ){\text{ 2.5 (m)}}\) (A1)(ft)(G2)
Note: Follow through from part (b)(i).
(iii) \(({h^2} = ){\text{ }}{5^2} – {2.5^2}\) (M1)
Notes: Award (M1) for correct substitution into Pythagoras’ theorem. Follow through from part (b)(ii).
\((h = ){\text{ 4.33 }}(4.33012 \ldots ){\text{ (m)}}\) (A1)(ft)(G2)
\(9.33 – 2 \times r\) (A1)
\(V = \frac{{\pi {r^2}}}{3} \times (9.33 – 2r)\) (M1)
Note: Award (M1) for correct substitution in the volume formula.
\(V = 3.11\pi {r^2} – \frac{2}{3}{\pi ^3}\) (AG)
\(6.22\pi r – 2\pi {r^2}\) (A1)(A1)
Notes: Award (A1) for \(6.22\pi r\), (A1) for \( – 2\pi {r^2}\).
If extra terms present, award at most (A1)(A0).
(i) \(6.22\pi r – 2\pi {r^2} = 0\) (M1)
Note: Award (M1) for setting their derivative from part (e) to 0.
\(r = 3.11{\text{ (m)}}\) (A1)(ft)(G2)
Notes: Award (A1) for identifying 3.11 as the answer.
Follow through from their answer to part (e).
(ii) \(\frac{1}{3}\pi {(3.11)^3}\;\;\;\)OR\(\;\;\;3.11\pi {(3.11)^2} – \frac{2}{3}\pi {(3.11)^3}\) (M1)
Note: Award (M1) for correct substitution into the correct volume formula.
\(31.5{\text{ (}}{{\text{m}}^3}{\text{)}}{\text{(31.4999}} \ldots {\text{)}}\) (A1)(ft)(G2)
Note: Follow through from their answer to part (f)(i).
Question
Nadia designs a wastepaper bin made in the shape of an open cylinder with a volume of \(8000{\text{ c}}{{\text{m}}^3}\).
Nadia decides to make the radius, \(r\) , of the bin \(5{\text{ cm}}\).
Merryn also designs a cylindrical wastepaper bin with a volume of \(8000{\text{ c}}{{\text{m}}^3}\). She decides to fix the radius of its base so that the total external surface area of the bin is minimized.
Let the radius of the base of Merryn’s wastepaper bin be \(r\) , and let its height be \(h\) .
Calculate
(i) the area of the base of the wastepaper bin;
(ii) the height, \(h\) , of Nadia’s wastepaper bin;
(iii) the total external surface area of the wastepaper bin.[7]
State whether Nadia’s design is practical. Give a reason.[2]
Write down an equation in \(h\) and \(r\) , using the given volume of the bin.[1]
Show that the total external surface area, \(A\) , of the bin is \(A = \pi {r^2} + \frac{{16000}}{r}\) .[2]
Write down \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\).[3]
(i) Find the value of \(r\) that minimizes the total external surface area of the wastepaper bin.
(ii) Calculate the value of \(h\) corresponding to this value of \(r\) .[5]
Determine whether Merryn’s design is an improvement upon Nadia’s. Give a reason.[2]
Answer/Explanation
Markscheme
(i) \({\text{Area}} = \pi {(5)^2}\) (M1)
\( = 78.5{\text{ (c}}{{\text{m}}^2}{\text{)}}\) (\(78.5398 \ldots \)) (A1)(G2)
Note: Accept \(25\pi \) .
(ii) \(8000 = 78.5398 \ldots \times h\) (M1)
\(h = 102{\text{ (cm)}}\) (\(101.859 \ldots \)) (A1)(ft)(G2)
Note: Follow through from their answer to part (a)(i).
(iii) \({\text{Area}} = \pi {(5)^2} + 2\pi (5)(101.859 \ldots )\) (M1)(M1)
Note: Award (M1) for their substitution in curved surface area formula, (M1) for addition of their two areas.
\( = 3280{\text{ (c}}{{\text{m}}^2}{\text{)}}\) (\(3278.53 \ldots \)) (A1)(ft)(G2)
Note: Follow through from their answers to parts (a)(i) and (ii).
No, it is too tall/narrow. (A1)(ft)(R1)
Note: Follow through from their value for \(h\).
\(8000 = \pi {r^2}h\) (A1)
\(A = \pi {r^2} + 2\pi r\left( {\frac{{8000}}{{\pi {r^2}}}} \right)\) (A1)(M1)
Note: Award (A1) for correct rearrangement of their part (c), (M1) for substitution of their rearrangement into area formula.
\( = \pi {r^2} + \frac{{16000}}{r}\) (AG)
\(\frac{{{\text{d}}A}}{{{\text{d}}r}} = 2\pi r – 16000{r^{ – 2}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi r\) , (A1) for \( – 16000\) (A1) for \({r^{ – 2}}\) . If an extra term is present award at most (A1)(A1)(A0).
(i) \(\frac{{{\text{d}}A}}{{{\text{d}}r}} = 0\) (M1)
\(2\pi {r^3} – 16000 = 0\) (M1)
\(r = 13.7{\text{ cm}}\) (\(13.6556 \ldots \)) (A1)(ft)
Note: Follow through from their part (e).
(ii) \(h = \frac{{8000}}{{\pi {{(13.65 \ldots )}^2}}}\) (M1)
\( = 13.7{\text{ cm}}\) (\(13.6556 \ldots \)) (A1)(ft)
Note: Accept \(13.6\) if \(13.7\) used.
Yes or No, accompanied by a consistent and sensible reason. (A1)(R1)
Note: Award (A0)(R0) if no reason is given.