Question
Five pipes labelled, “6 metres in length”, were delivered to a building site. The contractor measured each pipe to check its length (in metres) and recorded the following;
5.96, 5.95, 6.02, 5.95, 5.99.
(i) Find the mean of the contractor’s measurements.
(ii) Calculate the percentage error between the mean and the stated, approximate length of 6 metres.
Calculate \(\sqrt {{{3.87}^5} – {{8.73}^{ – 0.5}}} \), giving your answer
(i) correct to the nearest integer,
(ii) in the form \(a \times 10^k\), where 1 ≤ a < 10, \(k \in {\mathbb{Z}}\) .
Answer/Explanation
Markscheme
(i) Mean = (5.96 + 5.95 + 6.02 + 5.95 + 5.99) / 5 = 5.974 (5.97) (A1)
(ii) \({\text{% error}} = \frac{{error}}{{actualvalue}} \times 100\% \)
\( = \frac{{6 – 5.974}}{{5.974}} \times 100\% = 0.435\% \) (M1)(A1)(ft)
(M1) for correctly substituted formula.
Allow 0.503% as follow through from 5.97
Note: An answer of 0.433% is incorrect. (C3)
[3 marks]
number is 29.45728613
(i) Nearest integer = 29 (A1)
(ii) Standard form = 2.95 × 101 (accept 2.9 × 101) (A1)(ft)(A1)
Award (A1) for each correct term
Award (A1)(A0) for 2.95 × 10 (C3)
[3 marks]
Question
Write down the following numbers in increasing order.
\(3.5\), \(1.6 \times 10^{−19}\), \(60730\), \(6.073 \times 10^{5}\), \(0.006073 \times 10^6\), \(\pi\), \(9.8 \times 10^{−18}\).
Write down the median of the numbers in part (a).
State which of the numbers in part (a) is irrational.
Answer/Explanation
Markscheme
\(1.6 \times 10^{−19}\), \(9.8 \times 10^{−18}\), \(\pi\), \(3.5\), \(0.006073 \times 10^6\), \(60730\), \(6.073 \times 10^{5}\) (A4)
Award (A1) for \(\pi\) before 3.5
Award (A1) for \(1.6 \times 10^{−19}\) before \(9.8 \times 10^{−18}\)
Award (A1) for the three numbers containing 6073 in the correct order.
Award (A1) for the pair with negative indices placed before 3.5 and \(\pi\) and the remaining three numbers placed after (independently of the other three marks).
Award (A3) for numbers given in correct decreasing order.
Award (A2) for decreasing order with at most 1 error (C4)
[3 marks]
The median is 3.5. (A1)(ft)
Follow through from candidate’s list. (C1)
[1 mark]
\(\pi\) is irrational. (A1) (C1)
[1 mark]
Question
Consider the numbers \(2\), \(\sqrt 3 \), \( – \frac{2}{3}\) and the sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\).
Complete the table below by placing a tick in the appropriate box if the number is an element of the set, and a cross if it is not.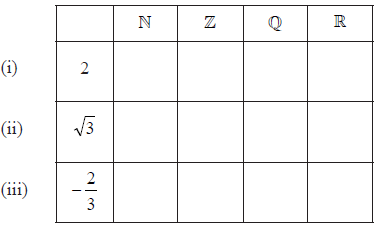
A function \(f\) is given by \(f(x) = 2{x^2} – 3x{\text{, }}x \in \{ – 2{\text{, }}2{\text{, }}3\} \).
Write down the range of function \(f\).
Answer/Explanation
Markscheme
 (A1)(A1)(A1) (C3)
(A1)(A1)(A1) (C3)
Note: Accept any symbol for ticks. Do not penalise if the other boxes are left blank.
[3 marks]
\({\text{Range}} = \{ 2{\text{, }}9{\text{, }}14\} \) (A1)(ft) (C1)
Note: Brackets not required.
[1 mark]
Question
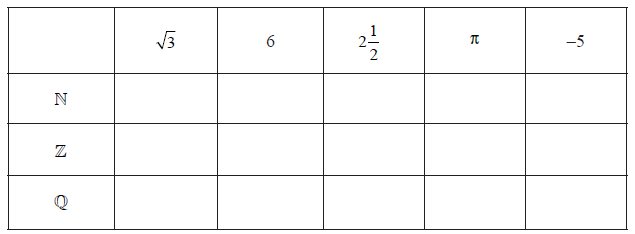
Consider the numbers \(\sqrt 3 \), \(6\), \(2\frac{1}{2}\), \(\pi \), \( – 5\), and the sets \(\mathbb{N}\), \(\mathbb{Z}\), and \(\mathbb{Q}\). Complete the following table by placing a tick in the appropriate box if the number is an element of the set.
Answer/Explanation
Markscheme
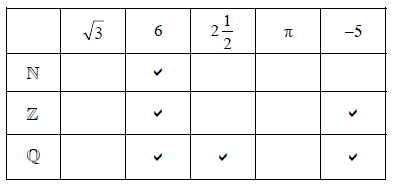
Note: Accept any symbol for ticks. Do not penalize if candidate had also indicated, by a different symbol, that the number is not an element of the set.
Row \(\mathbb{N}\) correct, no extra entries. (A1) (C1)
Row \(\mathbb{Z}\) (A1)(A1) (C2)
Note: Award (A1) for each correct tick and no extra entries. Award (A1) only for both ticks correct and 1 extra entry, (A0) otherwise.
Row \(\mathbb{Q}\) (A1)(A1)(A1) (C3)
Note: Award (A1) for each correct tick and no extra entries. Award (A2) only for all 3 correct and one extra entry. Award (A1) only for 2 correct and one extra entry. (A0) otherwise.
[6 marks]
Question
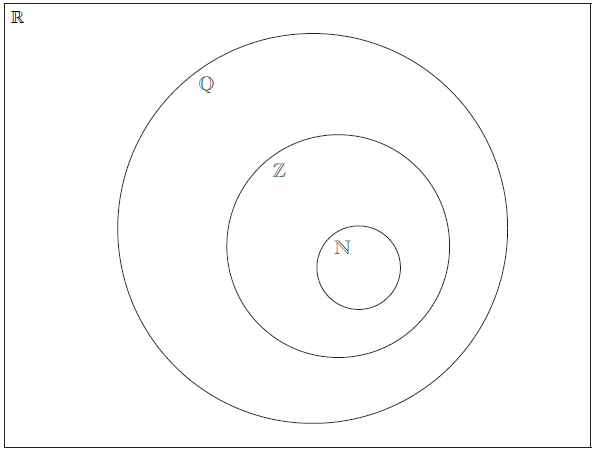
The Venn diagram shows the number sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\). Place each of the following numbers in the appropriate region of the Venn diagram.
\(\frac{{1}}{{4}}\), −3, π, cos 120°, 2.7 × 103, 3.4 × 10–2
Answer/Explanation
Markscheme
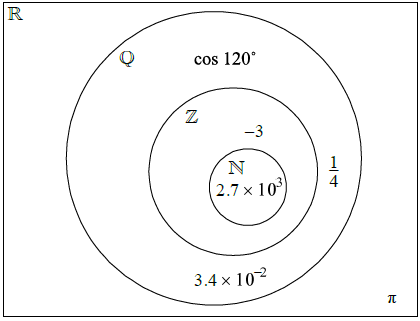 (A1)(A1)(A1)(A1)(A1)(A1) (C6)
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number placed once in the correct section. Accept equivalent forms for numbers.
[6 marks]
Question
The sets \(P\), \(Q\) and \(U\) are defined as
U = {Real Numbers} , P = {Positive Numbers} and Q = {Rational Numbers}.
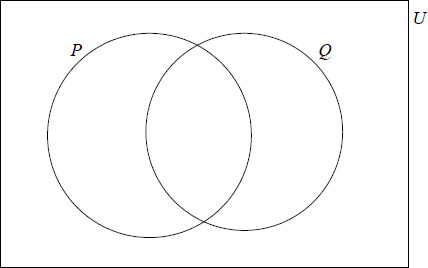
Write down in the correct region on the Venn diagram the numbers
\(\frac{{22}}{7}\) , \(5 \times {10^{ – 2}}\) , \(\sin (60^\circ )\) , \(0\) , \(\sqrt[3]{{ – 8}}\) , \( – \pi \).
Answer/Explanation
Markscheme
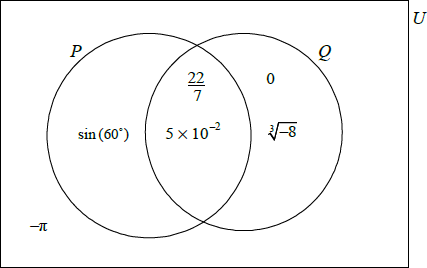 (A1)(A1)(A1)(A1)(A1)(A1) (C6)
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number placed once in the correct region. Accept equivalent forms for numbers.
[6 marks]
Question
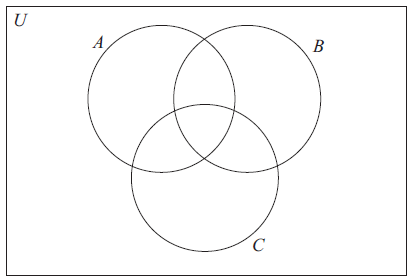
\(U\) is the set of all the positive integers less than or equal to \(12\).
\(A\) , \(B\) and \(C\) are subsets of \(U\) .
\[A = \{ 1{\text{, }}2{\text{, }}3{\text{, }}4{\text{, }}6{\text{, }}12\} \]\[B = \{ {\text{odd integers}}\} \]\[C = \{ 5{\text{, }}6{\text{, }}8\} \]
Write down the number of elements in \(A \cap C\) .
List the elements of \(B\) .
Complete the following Venn diagram with all the elements of \(U\) .
Answer/Explanation
Markscheme
\(1\) (one) (A1) (C1)
Note: \(6\), \(\{6\} \) or \(\{1\} \) earns no marks.
[1 mark]
\(1\), \(3\), \(5\), \(7\), \(9\), \(11\) (A1) (C1)
Note: Do not penalise if braces, parentheses or brackets are seen.
[1 mark]
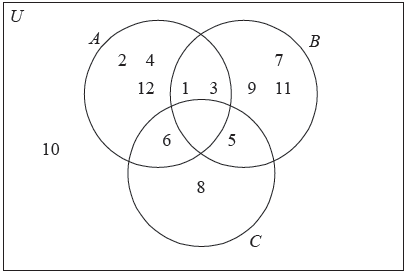 (A1)(A1)(ft)(A1)(ft)(A1)(ft) (C4)
(A1)(A1)(ft)(A1)(ft)(A1)(ft) (C4)
Notes: Award (A1) for the empty set \(A \cap B \cap C\) .
Award (A1)(ft) for the correct placement of \(6\), \(5\), \(1\) and \(3\).
Award (A1)(ft) for the correct placement of \(2\), \(4\), \(12\), \(7\), \(9\), \(11\), \(8\).
Award (A1)(ft) for the correct placement of \(10\).
Follow through from part (b).
[4 marks]
Question
Consider c = 5200 and d = 0.0000037.
Write down the value of r = c × d.
Write down your value of r in the form a × 10k, where 1 ≤ a < 10 and \(k \in \mathbb{Z}\).
Consider the following statements about c, d and r. Only three of these statements are true.
Circle the true statements.

Answer/Explanation
Markscheme
r = 0.01924 (A1) (C1)
Note: Accept 0.0192 and 0.019
[1 mark]
r = 1.924 × 10−2 (A1)(ft)(A1)(ft) (C2)
Notes: Award (A1) for 1.924, (A1) for 10−2. Accept 1.92 and 1.9. Follow through from their part (a).
[2 marks]
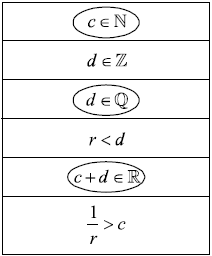 (A1)(A1)(A1) (C3)
(A1)(A1)(A1) (C3)
Notes: Award (A1) for each true statement circled. Do not follow through from part (a). Award (A1)(A1)(A0) if 1 extra term seen. Award (A1)(A0)(A0) if 2 extra terms seen. Award (A0)(A0)(A0) if all terms circled. Accept other indications of the correct statements i.e. highlighted or ticks.
[3 marks]
Question
\(U = \{ x|x{\text{ is an integer, }}2 < x < 10\}\)
A and B are subsets of U such that A = {multiples of 3}, B = {factors of 24}.
List the elements of
(i) U ;
(ii) B .
Write down the elements of U on the Venn diagram.
Write down \(n (A \cap B)\).
Answer/Explanation
Markscheme
(i) 3, 4, 5, 6, 7, 8, 9 (A1)
(ii) 3, 4, 6, 8 (A1)(ft) (C2)
Notes: Follow through from part (a)(i).
[2 marks]
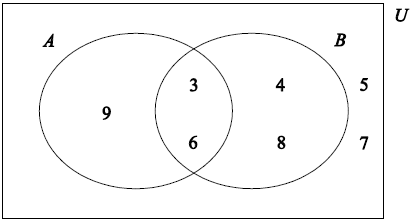
(A1)(ft) for their 3, 6
(A1)(ft) for their 4, 8, 9
(A1)(ft) for their 5, 7 (A1)(ft)(A1)(ft)(A1)(ft) (C3)
Note: Follow through from their universal set and set B in part (a).
[3 marks]
2 (A1)(ft) (C1)
Note: Follow through from their Venn diagram.
[1 mark]
Question
Consider the numbers 3, −5 , \(\sqrt{7}\), \(2^{−3}\) and 1.75.
Complete the table below, placing a tick () to show which of the number sets, \(\mathbb{N}, \mathbb{Q} {\text{ and }} \mathbb{R}\) these numbers belong to. The first row has been completed as an example.

Answer/Explanation
Markscheme
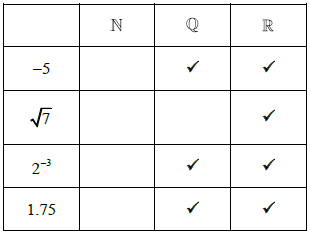
(A1) for \(\mathbb{N}\) column correct.
(A2) for \(\mathbb{R}\) column correct, award (A1) if one is missing, award (A0) if two or more
missing.
(A3) for \(\mathbb{Q}\) column correct, award (A2) for two correctly placed and no extra entries, award (A1) for one correctly placed
and no extra entries or
placed in all entries. (A6) (C6)
Examiners report
Question
The following Venn diagram shows the relationship between the sets of numbers
\[\mathbb{N},{\text{ }}\mathbb{Z}{\text{, }}\mathbb{Q}{\text{ and }}\mathbb{R}{\text{.}}\]
The number –3 belongs to the set of \(\mathbb{Z}{\text{, }}\mathbb{Q}\) and \(\mathbb{R}\), but not \(\mathbb{N}\), and is placed in the appropriate position on the Venn diagram as an example.
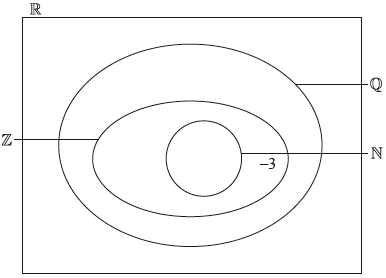
Write down the following numbers in the appropriate place in the Venn diagram.
a. 4 [1]
b. \(\frac{1}{3}\)[1]
Answer/Explanation
Markscheme
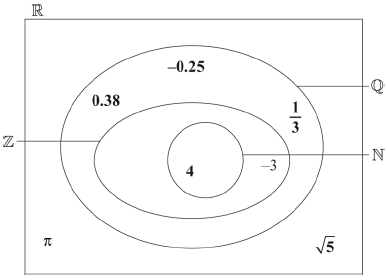 (A1)(A1)(A1)(A1)(A1)(A1) (C6)
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.
[1 mark]
 (A1)(A1)(A1)(A1)(A1)(A1) (C6)
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.
[1 mark]
 (A1)(A1)(A1)(A1)(A1)(A1) (C6)
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.
[1 mark]
 (A1)(A1)(A1)(A1)(A1)(A1) (C6)
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.
[1 mark]
 (A1)(A1)(A1)(A1)(A1)(A1) (C6)
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.
[1 mark]
 (A1)(A1)(A1)(A1)(A1)(A1) (C6)
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.
[1 mark]
Question
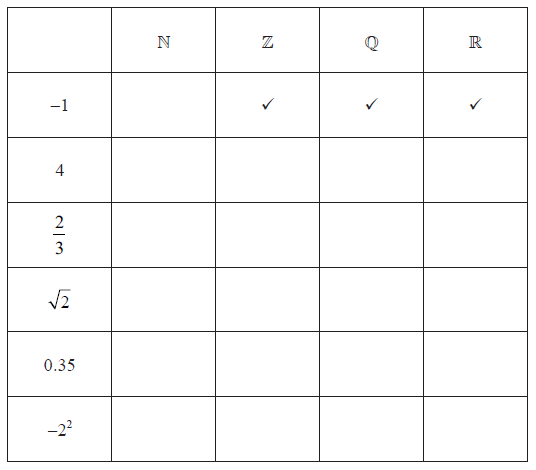
Consider the numbers \( – 1,\,\,4,\,\,\frac{2}{3},\,\,\sqrt 2 ,\,\,0.35\) and \( – {2^2}\).
Complete the following table by placing a tick () to indicate if the number is an element of the number set. The first row has been completed as an example.
Answer/Explanation
Markscheme
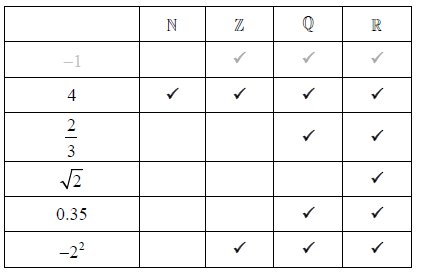
(A1)(A1)(A1)(A1)(A2) (C6)
Note: Row 1 has been given in the question.
Row 2 to row 5: Award (A1) for each correct row.
Row 6: Award (A1) for both \(\mathbb{N}\) not selected and \(\mathbb{Z}\) selected; award (A1) for both \(\mathbb{Q}\) and \(\mathbb{R}\) selected. Do not penalize if crosses (or similar) appear in the empty cells.
Question
The following table shows four different sets of numbers: \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\).

Complete the second column of the table by giving one example of a number from each set.
Josh states: “Every integer is a natural number”.
Write down whether Josh’s statement is correct. Justify your answer.
Answer/Explanation
Markscheme
 (A1)(A1)(A1)(A1)(C4)
(A1)(A1)(A1)(A1)(C4)
[4 marks]
Incorrect (A1)
Natural numbers are positive integers. Integers can also be negative. (or equivalent) (R1) (C2)
Note: Accept a correct justification. Do not award (R0)(A1).
Accept: a statement with an example of an integer which is not natural.
[2 marks]

