Question
The line \({L_1}\) has equation \(2y – x – 7 = 0\) and is shown on the diagram.
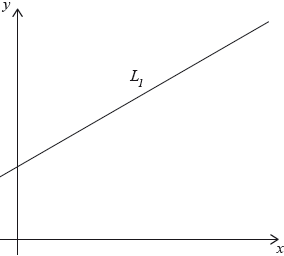
The point A has coordinates \((1,{\text{ }}4)\).
The point C has coordinates \((5,{\text{ }}12)\). M is the midpoint of AC.
The straight line, \({L_2}\), is perpendicular to AC and passes through M.
The point D is the intersection of \({L_1}\) and \({L_2}\).
The length of MD is \(\frac{{\sqrt {45} }}{2}\).
The point B is such that ABCD is a rhombus.
Show that A lies on \({L_1}\).[2]
Find the coordinates of M.[2]
Find the length of AC.[2]
Show that the equation of \({L_2}\) is \(2y + x – 19 = 0\).[5]
Find the coordinates of D.[2]
Write down the length of MD correct to five significant figures.[1]
Find the area of ABCD.[3]
Answer/Explanation
Markscheme
\(2 \times 4 – 1 – 7 = 0\) (or equivalent) (R1)
Note: For (R1) accept substitution of \(x = 1\) or \(y = 4\) into the equation followed by a confirmation that \(y = 4\) or \(x = 1\).
(since the point satisfies the equation of the line,) A lies on \({L_1}\) (A1)
Note: Do not award (A1)(R0).[2 marks]
\(\frac{{1 + 5}}{2}\) OR \(\frac{{4 + 12}}{2}\) seen (M1)
Note: Award (M1) for at least one correct substitution into the midpoint formula.
\((3,{\text{ }}8)\) (A1)(G2)
Notes: Accept \(x = 3,{\text{ }}y = 8\).
Award (M1)(A0) for \(\left( {\frac{{1 + 5}}{2},{\text{ }}\frac{{4 + 12}}{2}} \right)\).
Award (G1) for each correct coordinate seen without working.[2 marks]
\(\sqrt {{{(5 – 1)}^2} + {{(12 – 4)}^2}} \) (M1)
Note: Award (M1) for a correct substitution into distance between two points formula.
\( = 8.94{\text{ }}\left( {4\sqrt 5 ,{\text{ }}\sqrt {80} ,{\text{ }}8.94427 \ldots } \right)\) (A1)(G2)[2 marks]
gradient of \({\text{AC}} = \frac{{12 – 4}}{{5 – 1}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = 2\) (A1)
Note: Award (M1)(A1) for gradient of \({\text{AC}} = 2\) with or without working
gradient of the normal \( = – \frac{1}{2}\) (M1)
Note: Award (M1) for the negative reciprocal of their gradient of AC.
\(y – 8 = – \frac{1}{2}(x – 3)\) OR \(8 = – \frac{1}{2}(3) + c\) (M1)
Note: Award (M1) for substitution of their point and gradient into straight line formula. This (M1) can only be awarded where \( – \frac{1}{2}\) (gradient) is correctly determined as the gradient of the normal to AC.
\(2y – 16 = – (x – 3)\) OR \( – 2y + 16 = x – 3\) OR \(2y = – x + 19\) (A1)
Note: Award (A1) for correctly removing fractions, but only if their equation is equivalent to the given equation.
\(2y + x – 19 = 0\) (AG)
Note: The conclusion \(2y + x – 19 = 0\) must be seen for the (A1) to be awarded.
Where the candidate has shown the gradient of the normal to \({\text{AC}} = – 0.5\), award (M1) for \(2(8) + 3 – 19 = 0\) and (A1) for (therefore) \(2y + x – 19 = 0\).
Simply substituting \((3,{\text{ }}8)\) into the equation of \({L_2}\) with no other prior working, earns no marks.[5 marks]
\((6,{\text{ }}6.5)\) (A1)(A1)(G2)
Note: Award (A1) for 6, (A1) for 6.5. Award a maximum of (A1)(A0) if answers are not given as a coordinate pair. Accept \(x = 6,{\text{ }}y = 6.5\).
Award (M1)(A0) for an attempt to solve the two simultaneous equations \(2y – x – 7 = 0\) and \(2y + x – 19 = 0\) algebraically, leading to at least one incorrect or missing coordinate.[2 marks]
3.3541 (A1)
Note: Answer must be to 5 significant figures.[1 mark]
\(2 \times \frac{1}{2} \times \sqrt {80} \times \frac{{\sqrt {45} }}{2}\) (M1)(M1)
Notes: Award (M1) for correct substitution into area of triangle formula.
If their triangle is a quarter of the rhombus then award (M1) for multiplying their triangle by 4.
If their triangle is a half of the rhombus then award (M1) for multiplying their triangle by 2.
OR
\(\frac{1}{2} \times \sqrt {80} \times \sqrt {45} \) (M1)(M1)
Notes: Award (M1) for doubling MD to get the diagonal BD, (M1) for correct substitution into the area of a rhombus formula.
Award (M1)(M1) for \(\sqrt {80} \times \) their (f).
\( = 30\) (A1)(ft)(G3)
Notes: Follow through from parts (c) and (f).
\(8.94 \times 3.3541 = 29.9856 \ldots \)[3 marks]
Question
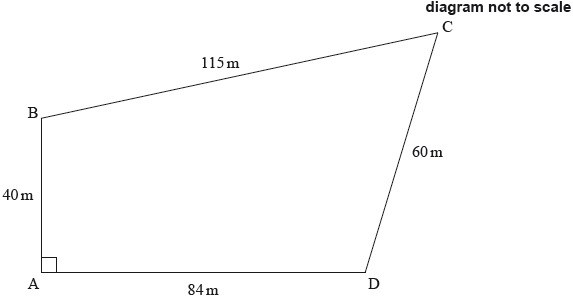
Abdallah owns a plot of land, near the river Nile, in the form of a quadrilateral ABCD.
The lengths of the sides are \({\text{AB}} = {\text{40 m, BC}} = {\text{115 m, CD}} = {\text{60 m, AD}} = {\text{84 m}}\) and angle \({\rm{B\hat AD}} = 90^\circ \).
This information is shown on the diagram.
The formula that the ancient Egyptians used to estimate the area of a quadrilateral ABCD is
\({\text{area}} = \frac{{({\text{AB}} + {\text{CD}})({\text{AD}} + {\text{BC}})}}{4}\).
Abdallah uses this formula to estimate the area of his plot of land.
Show that \({\text{BD}} = 93{\text{ m}}\) correct to the nearest metre.[2]
Calculate angle \({\rm{B\hat CD}}\).[3]
Find the area of ABCD.[4]
Calculate Abdallah’s estimate for the area.[2]
Find the percentage error in Abdallah’s estimate.[2]
Answer/Explanation
Markscheme
\({\text{B}}{{\text{D}}^2} = {40^2} + {84^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras.
Accept correct substitution into cosine rule.
\({\text{BD}} = 93.0376 \ldots \) (A1)
\( = 93\) (AG)
Note: Both the rounded and unrounded value must be seen for the (A1) to be awarded.[2 marks]
\(\cos C = \frac{{{{115}^2} + {{60}^2} – {{93}^2}}}{{2 \times 115 \times 60}}{\text{ }}({93^2} = {115^2} + {60^2} – 2 \times 115 \times 60 \times \cos C)\) (M1)(A1)
Note: Award (M1) for substitution into cosine formula, (A1) for correct substitutions.
\( = 53.7^\circ {\text{ }}(53.6679 \ldots ^\circ )\) (A1)(G2)[3 marks]
\(\frac{1}{2}(40)(84) + \frac{1}{2}(115)(60)\sin (53.6679 \ldots )\) (M1)(M1)(A1)(ft)
Note: Award (M1) for correct substitution into right-angle triangle area. Award (M1) for substitution into area of triangle formula and (A1)(ft) for correct substitution.
\( = 4460{\text{ }}{{\text{m}}^2}{\text{ }}(4459.30 \ldots {\text{ }}{{\text{m}}^2})\) (A1)(ft)(G3)
Notes: Follow through from part (b).[4 marks]
\(\frac{{(40 + 60)(84 + 115)}}{4}\) (M1)
Note: Award (M1) for correct substitution in the area formula used by ‘Ancient Egyptians’.
\( = 4980{\text{ }}{{\text{m}}^2}{\text{ }}(4975{\text{ }}{{\text{m}}^2})\) (A1)(G2)[2 marks]
\(\left| {\frac{{4975 – 4459.30 \ldots }}{{4459.30 \ldots }}} \right| \times 100\) (M1)
Notes: Award (M1) for correct substitution into percentage error formula.
\( = 11.6{\text{ }}(\% ){\text{ }}(11.5645 \ldots )\) (A1)(ft)(G2)
Notes: Follow through from parts (c) and (d)(i).[2 marks]
Question
The Tower of Pisa is well known worldwide for how it leans.
Giovanni visits the Tower and wants to investigate how much it is leaning. He draws a diagram showing a non-right triangle, ABC.
On Giovanni’s diagram the length of AB is 56 m, the length of BC is 37 m, and angle ACB is 60°. AX is the perpendicular height from A to BC.
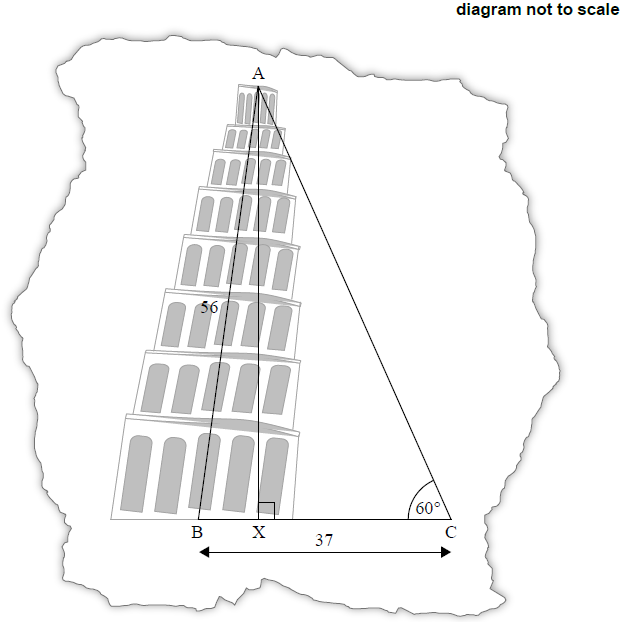
Giovanni’s tourist guidebook says that the actual horizontal displacement of the Tower, BX, is 3.9 metres.
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree.[5]
Use Giovanni’s diagram to calculate the length of AX.[2]
Use Giovanni’s diagram to find the length of BX, the horizontal displacement of the Tower.[2]
Find the percentage error on Giovanni’s diagram.[2]
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.
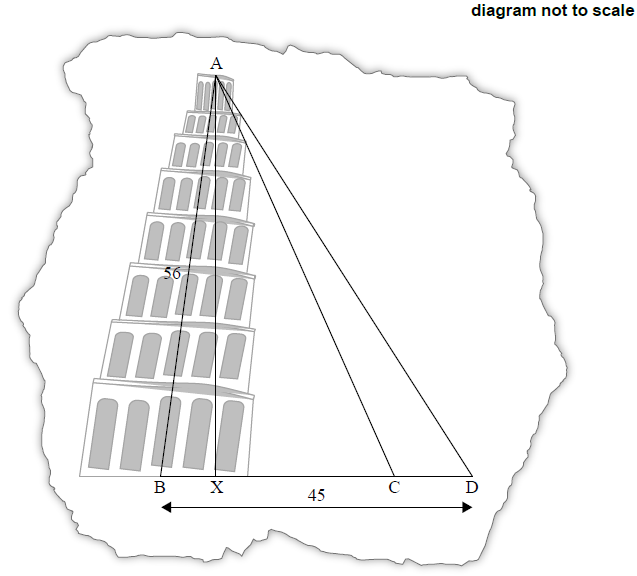
Find the angle of elevation of A from D.[3]
Answer/Explanation
Markscheme
\(\frac{{{\text{sin BAC}}}}{{37}} = \frac{{{\text{sin 60}}}}{{56}}\) (M1)(A1)
Note: Award (M1) for substituting the sine rule formula, (A1) for correct substitution.
angle \({\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}\) = 34.9034…° (A1)
Note: Award (A0) if unrounded answer does not round to 35. Award (G2) if 34.9034… seen without working.
angle \({\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}\) = 180 − (34.9034… + 60) (M1)
Note: Award (M1) for subtracting their angle BAC + 60 from 180.
85.0965…° (A1)
85° (AG)
Note: Both the unrounded and rounded value must be seen for the final (A1) to be awarded. If the candidate rounds 34.9034…° to 35° while substituting to find angle \({\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}\), the final (A1) can be awarded but only if both 34.9034…° and 35° are seen.
If 85 is used as part of the workings, award at most (M1)(A0)(A0)(M0)(A0)(AG). This is the reverse process and not accepted.
sin 85… × 56 (M1)
= 55.8 (55.7869…) (m) (A1)(G2)
Note: Award (M1) for correct substitution in trigonometric ratio.
\(\sqrt {{{56}^2} – 55.7869{ \ldots ^2}} \) (M1)
Note: Award (M1) for correct substitution in the Pythagoras theorem formula. Follow through from part (a)(ii).
OR
cos(85) × 56 (M1)
Note: Award (M1) for correct substitution in trigonometric ratio.
= 4.88 (4.88072…) (m) (A1)(ft)(G2)
Note: Accept 4.73 (4.72863…) (m) from using their 3 s.f answer. Accept equivalent methods.[2 marks]
\(\left| {\frac{{4.88 – 3.9}}{{3.9}}} \right| \times 100\) (M1)
Note: Award (M1) for correct substitution into the percentage error formula.
= 25.1 (25.1282) (%) (A1)(ft)(G2)
Note: Follow through from part (a)(iii).[2 marks]
\({\text{ta}}{{\text{n}}^{ – 1}}\left( {\frac{{55.7869 \ldots }}{{40.11927 \ldots }}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their 40.11927… seen. Award (M1) for correct substitution into trigonometric ratio.
OR
(37 − 4.88072…)2 + 55.7869…2
(AC =) 64.3725…
64.3726…2 + 82 − 2 × 8 × 64.3726… × cos120
(AD =) 68.7226…
\(\frac{{{\text{sin 120}}}}{{68.7226 \ldots }} = \frac{{{\text{sin A}}\mathop {\text{D}}\limits^ \wedge {\text{C}}}}{{64.3725 \ldots }}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their correct values seen, (M1) for correct substitution into the sine formula.
= 54.3° (54.2781…°) (A1)(ft)(G2)
Note: Follow through from part (a). Accept equivalent methods.[3 marks]
