Question
A race track is made up of a rectangular shape \(750{\text{ m}}\) by \(500{\text{ m}}\) with semi-circles at each end as shown in the diagram.
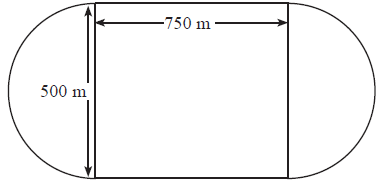
Michael drives around the track once at an average speed of \(140{\text{ km}}{{\text{h}}^{ – 1}}\).
Calculate the distance that Michael travels.[2]
Calculate how long Michael takes in seconds.[4]
Answer/Explanation
Markscheme
Unit penalty (UP) may apply in this question.
\({\text{Distance}} = \pi \times 500 + 2 \times 750\) (M1)
(UP) \( = 3070{\text{ m}}\) (A1) (C2)[2 marks]
Unit penalty (UP) may apply in this question.
\({\text{140 km}}{{\text{h}}^{ – 1}} = \frac{{140 \times 1000}}{{60 \times 60}}{\text{ m}}{{\text{s}}^{ – 1}}\) (M1)
\( = 38.9{\text{ m}}{{\text{s}}^{ – 1}}\) (A1)
\({\text{Time}} = \frac{{3070}}{{38.889}}\) (M1)
(UP) \( = 78.9{\text{ seconds}}\) (accept \(79.0\) seconds) (A1)(ft) (C4)[4 marks]
Question
José stands 1.38 kilometres from a vertical cliff.
Express this distance in metres.[1]
José estimates the angle between the horizontal and the top of the cliff as 28.3° and uses it to find the height of the cliff.
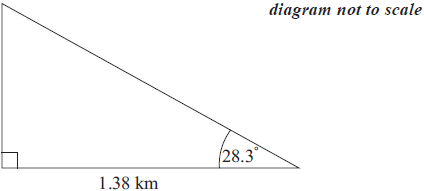
Find the height of the cliff according to José’s calculation. Express your answer in metres, to the nearest whole metre.[3]
José estimates the angle between the horizontal and the top of the cliff as 28.3° and uses it to find the height of the cliff.
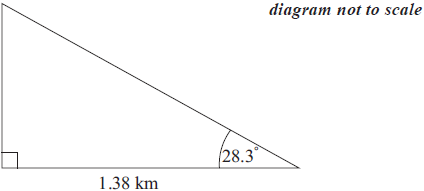
The actual height of the cliff is 718 metres. Calculate the percentage error made by José when calculating the height of the cliff.[2]
Answer/Explanation
Markscheme
1380 (m) (A1) (C1)[1 mark]
\(1380\tan 28.3\) (M1)
\( = 743.05 \ldots \) . (A1)(ft)
\( = 743\) (m) (A1)(ft) (C3)
Notes: Award (M1) for correct substitution in tan formula or equivalent, (A1)(ft) for their 743.05 seen, (A1)(ft) for their answer correct to the nearest m.[3 marks]
\({\text{percentage error}} = \frac{{743.05 \ldots – 718}}{{718}} \times 100\) (M1)
Note: Award (M1) for correct substitution in formula.
= 3.49 % (% symbol not required) (A1)(ft) (C2)
Notes: Accept 3.48 % for use of 743.
Accept negative answer.[2 marks]
Question
Ross is a star that is 82 414 080 000 000 km away from Earth. A spacecraft, launched from Earth, travels at 48 000 kmh–1 towards Ross.
Calculate the exact time, in hours, for the spacecraft to reach the star Ross.[2]
Give your answer to part (a) in years. (Assume 1 year = 365 days)[2]
Give your answer to part (b) in the form a×10k, where 1 ≤ a < 10 and \(k \in \mathbb{Z}\).[2]
Answer/Explanation
Markscheme
\(\frac{{{\text{82 414 080 000 000}}}}{{48\;000}}\) (M1)
Note: Award (M1) for correct substitution in correct formula.
1 716 960 000 (hours) (A1) (C2)[2 marks]
\(\frac{{{\text{their (a)}}}}{{24 \times 365}}\) (M1)
196 000 (years) (A1)(ft) (C2)
Note: Award (A1)(ft) from their part (a).[2 marks]
1.96×105 (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for 1.96 (accept 1.96000), (A1)(ft) for 105 . Follow through from their answer to part (b).[2 marks]
Question
Temi’s sailing boat has a sail in the shape of a right-angled triangle, \({\text{ABC}}{\text{.}}\,\,\,{\text{BC}} = \,\,5.45{\text{m}}\),
angle \({\text{CAB}} = {76^{\text{o}}}\) and angle \({\text{ABC}} = {90^{\text{o}}}\).
Calculate \({\text{AC}}\), the height of Temi’s sail.[2]
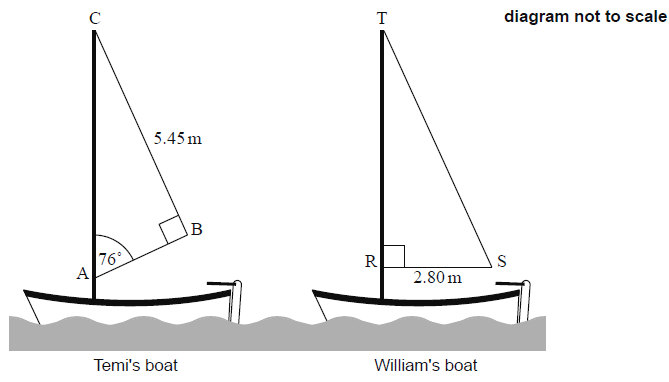
William also has a sailing boat with a sail in the shape of a right-angled triangle, \({\text{TRS}}\).
\({\text{RS}}\,\,{\text{ = }}\,\,{\text{2}}{\text{.80m}}\). The area of William’s sail is \({\text{10}}{\text{.7}}\,{{\text{m}}^2}\).
Calculate \({\text{RT}}\), the height of William’s sail.[2]
Answer/Explanation
Markscheme
Units are required in parts (a) and (b).
\({\text{sin}}\,\,{76^{\text{o}}} = \,\,\frac{{5.45}}{{{\text{AC}}}}\) (M1)
Note: Award (M1) for correct substitution into correct trig formula.
\({\text{AC}}\,\, = \,\,5.62{\text{m}}\,\,\,( = 5.61684…{\text{m}})\) (A1) (C2)
Note: The answer is \(5.62{\text{m}}\), the units are required. [2 marks]
\(\frac{1}{2}\,\, \times \,\,2.80\,\, \times \,\,{\text{RT}}\,\,{\text{ = }}\,\,{\text{10}}{\text{.7}}\) (M1)
Note: Award (M1) for correct substitution into area of a triangle formula or equivalent.
\({\text{RT}}\,\,{\text{ = }}\,\,{\text{7}}{\text{.64}}\,{\text{m (7}}{\text{.64285}}…{\text{m)}}\) (A1) (C2)
Note: The answer is \({\text{7}}{\text{.64}}\,{\text{m}}\), the units are required.[2 marks]
Question
Assume that the Earth is a sphere with a radius, \(r\) , of \(6.38 \times {10^3}\,{\text{km}}\) .
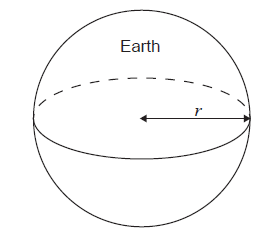
i) Calculate the surface area of the Earth in \({\text{k}}{{\text{m}}^2}\).
ii) Write down your answer to part (a)(i) in the form \(a \times {10^k}\) , where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\) .[4]
The surface area of the Earth that is covered by water is approximately \(3.61 \times {10^8}{\text{k}}{{\text{m}}^2}\) .
Calculate the percentage of the surface area of the Earth that is covered by water.[2]
Answer/Explanation
Markscheme
i) \(4\pi {(6.38 \times {10^3})^2}\) (M1)
Note: Award (M1) for correct substitution into the surface area of a sphere formula.
\( = 512\,000\,000\,\,\,(511506576,\,\,162\,817\,600\pi )\) (A1) (C2)
Note: Award at most (M1)(A0) for use of \(3.14\) for \(\pi \), which will give an answer of \(511\,247\,264\).
ii) \(5.12 \times {10^8}\,\,\,(5.11506… \times {10^8},\,\,1.628176\pi \times {10^8})\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A1) for \(5.12\) and (A1) for \( \times {10^8}\).
Award (A0)(A0) for answers of the type: \(5.12 \times {10^7}\).
Follow through from part (a)(i).
\(\frac{{3.61 \times {{10}^8}}}{{5.11506…\,\, \times {{10}^8}}} \times 100\) OR \(\frac{{3.61}}{{5.11506…\,}} \times 100\) OR \(0.705758… \times 100\) (M1)
Note: Award (M1) for correct substitution. Multiplication by \(100\) must be seen.
\( = 70.6\,(\% )\,\,\,\,(70.5758…\,(\% ))\) (A1)(ft) (C2)
Note: Follow through from part (a). Accept the use of \(3\) sf answers, which gives a final answer of \(70.5\,(\% )\,\,\,\,(70.5758…\,(\% ))\) .
Question
A ladder is standing on horizontal ground and leaning against a vertical wall. The length of the ladder is \(4.5\) metres. The distance between the bottom of the ladder and the base of the wall is \(2.2\) metres.
Use the above information to sketch a labelled diagram showing the ground, the ladder and the wall.[1]
Calculate the distance between the top of the ladder and the base of the wall.[2]
Calculate the obtuse angle made by the ladder with the ground.[3]
Answer/Explanation
Markscheme
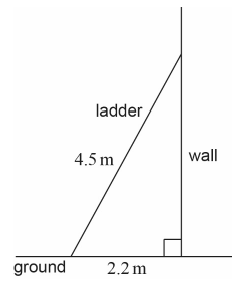
(A1) (C1)
Notes: Award (A1) for drawing an approximately right angled triangle, with correct labelling of the distances \(4.5\,({\text{m}})\) and \(2.2\,({\text{m}})\).
\(\sqrt {\,{{4.5}^2} – {{2.2}^2}} \,\,\,({\text{accept eqivalent }}eg\,\,{d^2} + {2.2^2} = {4.5^2})\) (M1)
\( = 3.93\,({\text{m}})\,\,\,\left( {\sqrt {\,15.41} \,({\text{m}}),\,\,3.92555…\,({\text{m}})} \right)\) (A1) (C2)
Note: Award (M1) for a correct substitution in the Pythagoras formula.
\(180^\circ – {\cos ^{ – 1}}\left( {\frac{{2.2}}{{4.5}}} \right)\) (M1)(M1)
OR
\(180^\circ – {\tan ^{ – 1}}\left( {\frac{{3.92555…}}{{2.2}}} \right)\) (M1)(M1)
OR
\(180^\circ – {\sin ^{ – 1}}\left( {\frac{{3.92555…}}{{4.5}}} \right)\) (M1)(M1)
Note: Award (M1) for a correct substitution in the correct trigonometric ratio.
Award (M1) for subtraction from \(180^\circ \) (this may be implied if the sum of their inverse of the trigonometric ratio and their final answer equals \(180\)).
\( = 119^\circ \,\,\,(119.267…^\circ )\) (A1)(ft) (C3)
Note: Follow through from their part (b) if cosine is not used. Accept \(119.239…\) or \(119.151…\) from use of \(3\) sf values.
Question
When Bermuda \({\text{(B)}}\), Puerto Rico \({\text{(P)}}\), and Miami \({\text{(M)}}\) are joined on a map using straight lines, a triangle is formed. This triangle is known as the Bermuda triangle.
According to the map, the distance \({\text{MB}}\) is \(1650\,{\text{km}}\), the distance \({\text{MP}}\) is \(1500\,{\text{km}}\) and angle \({\text{BMP}}\) is \(57^\circ \).
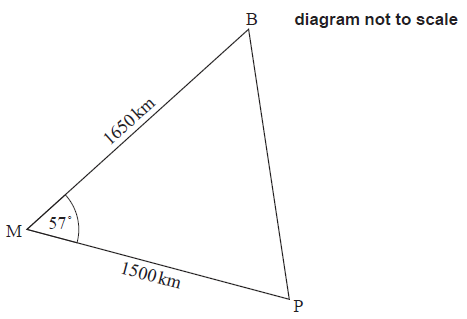
Calculate the distance from Bermuda to Puerto Rico, \({\text{BP}}\).[3]
Calculate the area of the Bermuda triangle.[3]
Answer/Explanation
Markscheme
\({\text{B}}{{\text{P}}^2} = {1650^2} + {1500^2} – 2 \times 1650 \times 1500\,\cos \,(57^\circ )\) (M1)(A1)
\(1510\,({\text{km}})\,\,\,\left( {1508.81…\,({\text{km}})} \right)\) (A1) (C3)
Notes: Award (M1) for substitution in the cosine rule formula, (A1) for correct substitution.
\(\frac{1}{2} \times 1650 \times 1500 \times \sin \,57^\circ \) (M1)(A1)
\( = 1\,040\,000\,({\text{k}}{{\text{m}}^2})\,\,\,\left( {1\,037\,854.82…\,({\text{k}}{{\text{m}}^2})} \right)\) (A1) (C3)
Note: Award (M1) for substitution in the area of triangle formula, (A1) for correct substitution.
Question
Each day a supermarket records the midday temperature and how many cold drinks are sold on that day. The following table shows the supermarket’s data for the last 6 days. This data is also shown on a scatter diagram.

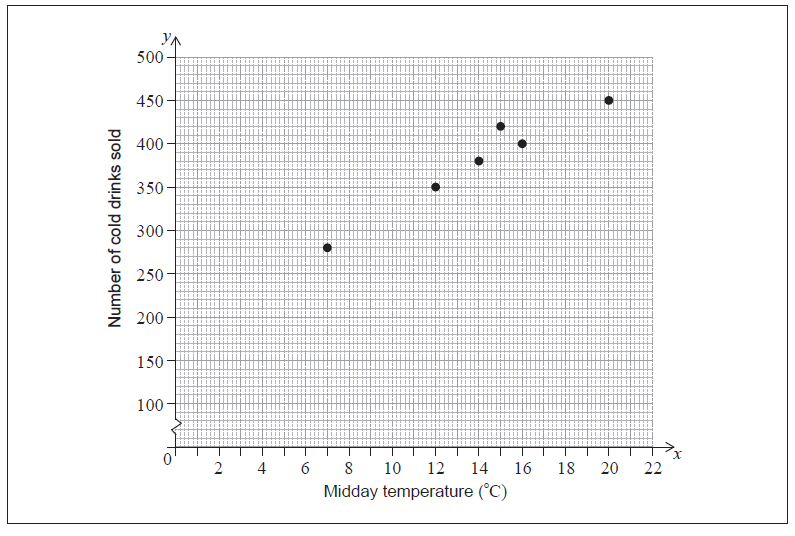
Write down
i) the mean temperature, \({\bar x}\) ;
ii) the mean number of cold drinks sold, \({\bar y}\) .[2]
Draw the line of best fit on the scatter diagram.[2]
Use the line of best fit to estimate the number of cold drinks that are sold on a day when the midday temperature is \(10\,^\circ {\text{C}}\).[2]
Answer/Explanation
Markscheme
i) \(14\) (A1)
ii) \(380\) (A1) (C2)
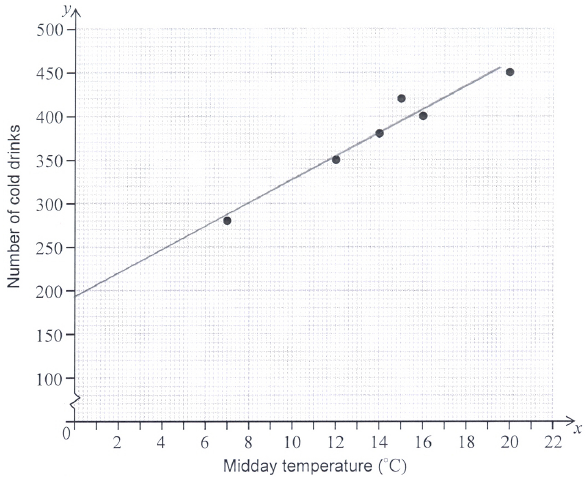
(A1)(ft)(A1) (C2)
Note: Award (A1)(ft) for a straight line going through their mean point, (A1) for intercepting the y-axis between \(160\) and \(220\) inclusive. Follow through from part (a).
an attempt to use their line of best fit to find \(y\) value at \(x = 10\) (M1)
Note: Award (M1) for an indication of use of their line of best fit (dotted lines or some indication of mark in the correct place on graph).
OR
\(13.4\,(10) + 192\) (M1)
Note: Award (M1) for correct substitution into the regression equation, \(y = 13.4x + 192\).
\( = 326\) (A1)(ft) (C2)
Note: Follow through from part (b). Accept answers between \(310\) and \(340\), inclusive.
Question
A snack container has a cylindrical shape. The diameter of the base is \(7.84\,{\text{cm}}\). The height of the container is \(23.4\,{\text{cm}}\). This is shown in the following diagram.
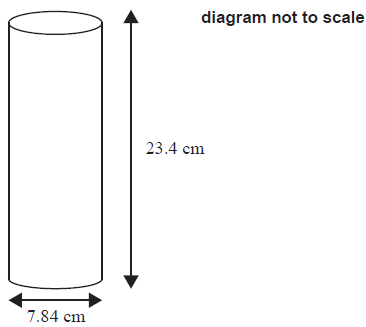
Write down the radius, in \({\text{cm}}\), of the base of the container.[1]
Calculate the area of the base of the container.[2]
Dan is going to paint the curved surface and the base of the snack container.
Calculate the area to be painted.[3]
Answer/Explanation
Markscheme
\(3.92\,({\text{cm}})\) (A1) (C1)
\(\pi \times {3.92^2}\) (M1)
\( = 48.3\,{\text{c}}{{\text{m}}^2}\,\,\,(15.3664\,\pi \,{\text{c}}{{\text{m}}^2},\,\,48.2749…\,{\text{c}}{{\text{m}}^2})\) (A1)(ft) (C2)
Note: Award (M1) for correct substitution in area of circle formula. Follow through from their part (a). The answer is \(48.3\,{\text{c}}{{\text{m}}^2}\), units are required.
\(2 \times \pi \times 3.92 \times 23.4 + 48.3\) (M1)(M1)
\(625\,{\text{c}}{{\text{m}}^2}\,\,\,(624.618…\,{\text{c}}{{\text{m}}^2})\) (A1)(ft) (C3)
Note: Award (M1) for correct substitution in curved surface area formula, (M1) for adding their answer to part (b). Follow through from their parts (a) and (b). The answer is \(625\,{\text{c}}{{\text{m}}^2}\), units are required.
Question
A type of candy is packaged in a right circular cone that has volume \({\text{100 c}}{{\text{m}}^{\text{3}}}\) and vertical height 8 cm.
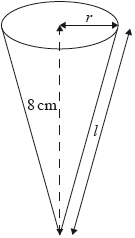
Find the radius, \(r\), of the circular base of the cone.[2]
Find the slant height, \(l\), of the cone.[2]
Find the curved surface area of the cone.[2]
Answer/Explanation
Markscheme
\(100 = \frac{1}{3}\pi {r^2}(8)\) (M1)
Note: Award (M1) for correct substitution into volume of cone formula.
\(r = 3.45{\text{ (cm) }}\left( {3.45494 \ldots {\text{ (cm)}}} \right)\) (A1) (C2)[2 marks]
\({l^2} = {8^2} + {(3.45494 \ldots )^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ theorem.
\(l = 8.71{\text{ (cm) }}\left( {8.71416 \ldots {\text{ (cm)}}} \right)\) (A1)(ft) (C2)
Note: Follow through from part (a).[2 marks]
\(\pi \times 3.45494 \ldots \times 8.71416 \ldots \) (M1)
Note: Award (M1) for their correct substitutions into curved surface area of a cone formula.
\( = 94.6{\text{ c}}{{\text{m}}^2}{\text{ }}(94.5836 \ldots {\text{ c}}{{\text{m}}^2})\) (A1)(ft) (C2)
Note: Follow through from parts (a) and (b). Accept \(94.4{\text{ c}}{{\text{m}}^2}\) from use of 3 sf values.[2 marks]
Question
The speed of light is \({\text{300}}\,{\text{000}}\) kilometres per second. The average distance from the Sun to the Earth is 149.6 million km.
A light-year is the distance light travels in one year and is equal to \({\text{9}}\,{\text{467}}\,{\text{280}}\) million km. Polaris is a bright star, visible from the Northern Hemisphere. The distance from the Earth to Polaris is 323 light-years.
Calculate the time, in minutes, it takes for light from the Sun to reach the Earth.[3]
Find the distance from the Earth to Polaris in millions of km. Give your answer in the form \(a \times {10^k}\) with \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\).[3]
Answer/Explanation
Markscheme
\(\frac{{149600000}}{{300000 \times 60}}\) (M1)(M1)
Note: Award (M1) for dividing the correct numerator (which can be presented in a different form such as \(149.6 \times {10^6}\) or \(1.496 \times {10^8}\)) by \({\text{300}}\,{\text{000}}\) and (M1) for dividing by 60.
\( = 8.31{\text{ }}({\text{minutes}}){\text{ }}(8.31111 \ldots {\text{, 8 minutes 19 seconds}})\) (A1) (C3)[3 marks]
\(323 \times 9467\,280\) (M1)
Note: Award (M1) for multiplying 323 by \(9\,467\,280\), seen with any power of 10; therefore only penalizing incorrect power of 10 once.
\( = 3.06 \times {10^9}{\text{ ( = }}3.05793 \ldots \times {10^9})\) (A1)(A1) (C3)
Note: Award (A1) for 3.06.
Award (A1) for \( \times {10^9}\)
Award (A0)(A0) for answers of the type: \(30.6 \times {10^8}\)[3 marks]
Question
A solid right circular cone has a base radius of 21 cm and a slant height of 35 cm.
A smaller right circular cone has a height of 12 cm and a slant height of 15 cm, and is removed from the top of the larger cone, as shown in the diagram.
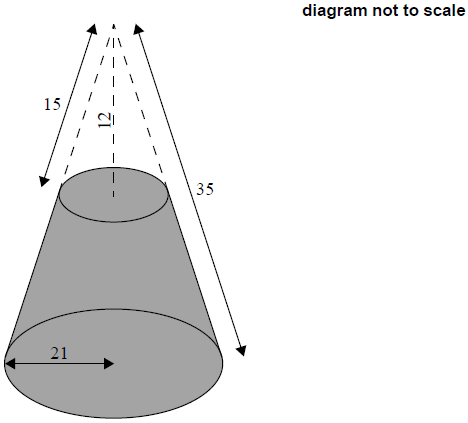
Calculate the radius of the base of the cone which has been removed.[2]
Calculate the curved surface area of the cone which has been removed.[2]
Calculate the curved surface area of the remaining solid.[2]
Answer/Explanation
Markscheme
\(\sqrt {{{15}^2} – {{12}^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras theorem.
OR
\(\frac{{{\text{radius}}}}{{21}} = \frac{{15}}{{35}}\) (M1)
Note: Award (M1) for a correct equation.
= 9 (cm) (A1) (C2)[2 marks]
\(\pi \times 9 \times 15\) (M1)
Note: Award (M1) for their correct substitution into curved surface area of a cone formula.
\( = 424\,\,{\text{c}}{{\text{m}}^2}\,\,\,\,\,\left( {135\pi ,\,\,424.115…{\text{c}}{{\text{m}}^2}} \right)\) (A1)(ft) (C2)
Note: Follow through from part (a).[2 marks]
\(\pi \times 21 \times 35 – 424.115…\) (M1)
Note: Award (M1) for their correct substitution into curved surface area of a cone formula and for subtracting their part (b).
\( = 1880\,\,{\text{c}}{{\text{m}}^2}\,\,\,\,\,\left( {600\pi ,\,\,1884.95…{\text{c}}{{\text{m}}^2}} \right)\) (A1)(ft) (C2)
Note: Follow through from part (b).[2 marks]
Question
A park in the form of a triangle, ABC, is shown in the following diagram. AB is 79 km and BC is 62 km. Angle A\(\mathop {\text{B}}\limits^ \wedge \)C is 52°.
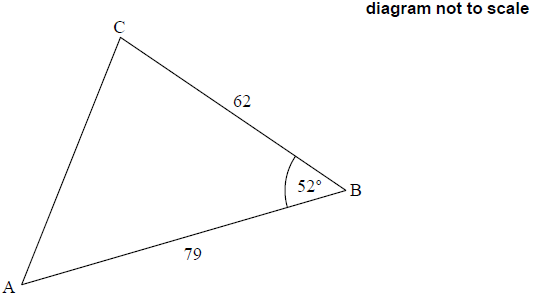
Calculate the length of side AC in km.[3]
Calculate the area of the park.[3]
Markscheme
(AC2 =) 622 + 792 − 2 × 62 × 79 × cos(52°) (M1)(A1)
Note: Award (M1) for substituting in the cosine rule formula, (A1) for correct substitution.
63.7 (63.6708…) (km) (A1) (C3)[3 marks]
\(\frac{1}{2}\) × 62 × 79 × sin(52°) (M1)(A1)
Note: Award (M1) for substituting in the area of triangle formula, (A1) for correct substitution.
1930 km2 (1929.83…km2) (A1) (C3)[3 marks]
Question
Julio is making a wooden pencil case in the shape of a large pencil. The pencil case consists of a cylinder attached to a cone, as shown.
The cylinder has a radius of r cm and a height of 12 cm.
The cone has a base radius of r cm and a height of 10 cm.
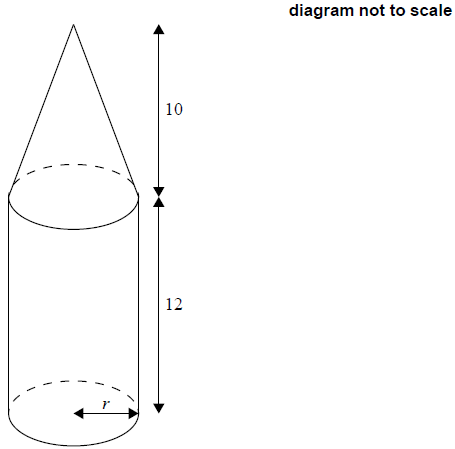
Find an expression for the slant height of the cone in terms of r.[2]
The total external surface area of the pencil case rounded to 3 significant figures is 570 cm2.
Using your graphic display calculator, calculate the value of r.[4]
Answer/Explanation
Markscheme
(slant height2 =) 102 + r 2 (M1)
Note: For correct substitution of 10 and r into Pythagoras’ Theorem.
\(\sqrt {{{10}^2} + {r^2}} \) (A1) (C2)[2 marks]
\(\pi {r^2} + 2\pi r \times 12 + \pi r\sqrt {100 + {r^2}} = 570\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution in curved surface area of cylinder and area of the base, (M1) for their correct substitution in curved surface area of cone, (M1) for adding their 3 surface areas and equating to 570. Follow through their part (a).
= 4.58 (4.58358…) (A1)(ft) (C4)
Note: Last line must be seen to award final (A1). Follow through from part (a).[4 marks]

