Question
Jenny has a circular cylinder with a lid. The cylinder has height 39 cm and diameter 65 mm.
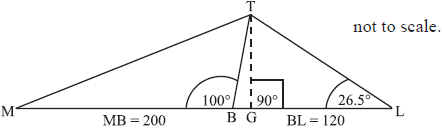
An old tower (BT) leans at 10° away from the vertical (represented by line TG).
The base of the tower is at B so that \({\text{M}}\hat {\rm B}{\text{T}} = 100^\circ \).
Leonardo stands at L on flat ground 120 m away from B in the direction of the lean.
He measures the angle between the ground and the top of the tower T to be \({\text{B}}\hat {\rm L}{\text{T}} = 26.5^\circ \).
Calculate the volume of the cylinder in cm3. Give your answer correct to two decimal places.[3]
The cylinder is used for storing tennis balls. Each ball has a radius of 3.25 cm.
Calculate how many balls Jenny can fit in the cylinder if it is filled to the top.[1]
(i) Jenny fills the cylinder with the number of balls found in part (b) and puts the lid on. Calculate the volume of air inside the cylinder in the spaces between the tennis balls.
(ii) Convert your answer to (c) (i) into cubic metres.[4]
(i) Find the value of angle \({\text{B}}\hat {\rm T}{\text{L}}\).
(ii) Use triangle BTL to calculate the sloping distance BT from the base, B to the top, T of the tower.[5]
Calculate the vertical height TG of the top of the tower.[2]
Leonardo now walks to point M, a distance 200 m from B on the opposite side of the tower. Calculate the distance from M to the top of the tower at T.[3]
Answer/Explanation
Markscheme
\(\pi \times 3.25^2 \times 39\) (M1)(A1)
(= 1294.1398)
Answer 1294.14 (cm3)(2dp) (A1)(ft)(G2)
(UP) not applicable in this part due to wording of question. (M1) is for substituting appropriate numbers from the problem into the correct formula, even if the units are mixed up. (A1) is for correct substitutions or correct answer with more than 2dp in cubic centimetres seen. Award (G1) for answer to > 2dp with no working and no attempt to correct to 2dp. Award (M1)(A0)(A1)(ft) for \(\pi \times {32.5^2} \times 39{\text{ c}}{{\text{m}}^3}\) (= 129413.9824) = 129413.98
Use of \(\pi = \frac{22}{7}\) or 3.142 etc is premature rounding and is awarded at most (M1)(A1)(A0) or (M1)(A0)(A1)(ft) depending on whether the intermediate value is seen or not. For all other incorrect substitutions, award (M1)(A0) and only follow through the 2 dp correction if the intermediate answer to more decimal places is seen. Answer given as a multiple of \(\pi\) is awarded at most (M1)(A1)(A0). As usual, an unsubstituted formula followed by correct answer only receives the G marks.[3 marks]
39/6.5 = 6 (A1)[1 mark]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) (i) Volume of one ball is \(\frac{4}{3} \pi \times 3.25^3 {\text{ cm}}^3\) (M1)
\({\text{Volume of air}} = \pi \times {3.25^2} \times 39 – 6 \times \frac{4}{3}\pi \times {3.25^3} = 431{\text{ c}}{{\text{m}}^3}\) (M1)(A1)(ft)(G2)
Award first (M1) for substituted volume of sphere formula or for numerical value of sphere volume seen (143.79… or 45.77… \( \times \pi\)). Award second (M1) for subtracting candidate’s sphere volume multiplied by their answer to (b). Follow through from parts (a) and (b) only, but negative or zero answer is always awarded (A0)(ft)
(UP) (ii) 0.000431m3 or 4.31×10−4 m3 (A1)(ft)[4 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) \({\text{Angle B}}\widehat {\text{T}}{\text{L}} = 180 – 80 – 26.5\) or \(180 – 90 – 26.5 – 10\) (M1)
\(= 73.5^\circ\) (A1)(G2)
(ii) \(\frac{{BT}}{{\sin (26.5^\circ )}} = \frac{{120}}{{\sin (73.5^\circ )}}\) (M1)(A1)(ft)
(UP) BT = 55.8 m (3sf) (A1)(ft)[5 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Unit penalty (UP) is applicable where indicated in the left hand column.
TG = 55.8sin(80°) or 55.8cos(10°) (M1)
(UP) = 55.0 m (3sf) (A1)(ft)(G2)
Apply (AP) if 0 missing[2 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Unit penalty (UP) is applicable where indicated in the left hand column.
\({\text{MT}}^2 = 200^2 + 55.8^2 – 2 \times 200 \times 55.8 \times \cos(100^\circ)\) (M1)(A1)(ft)
(UP) MT = 217 m (3sf) (A1)(ft)
Follow through only from part (ii)(a)(ii). Award marks at discretion for any valid alternative method.[3 marks]
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but
negative lengths are always awarded (A0)(ft).
The answers are (all 3sf)
(ii)(a) – 124 m (A0)(ft)
(ii)(b) 123 m (A0)
(ii)(c) 313 m (A0)
If radian mode has been used throughout the question, award (A0) to the first incorrect answer then follow through, but negative lengths are always awarded (A0)(ft)
Question
ABCDV is a solid glass pyramid. The base of the pyramid is a square of side 3.2 cm. The vertical height is 2.8 cm. The vertex V is directly above the centre O of the base.
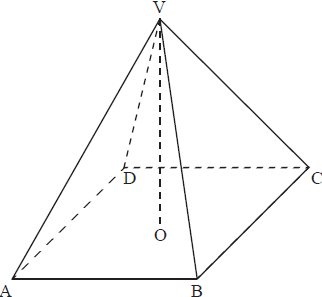
Calculate the volume of the pyramid.[2]
The glass weighs 9.3 grams per cm3. Calculate the weight of the pyramid.[2]
Show that the length of the sloping edge VC of the pyramid is 3.6 cm.[4]
Calculate the angle at the vertex, \({\text{B}}{\operatorname {\hat V}}{\text{C}}\).[3]
Calculate the total surface area of the pyramid.[4]
Answer/Explanation
Markscheme
Unit penalty (UP) is applicable in question parts (a), (b) and (e) only.
\({\text{V}} = \frac{1}{3} \times {3.2^2} \times 2.8\) (M1)
(M1) for substituting in correct formula
(UP) = 9.56 cm3 (A1)(G2)[2 marks]
Unit penalty (UP) is applicable in question parts (a), (b) and (e) only.
\(9.56 \times 9.3\) (M1)
(UP) = 88.9 grams (A1)(ft)(G2)[2 marks]
\(\frac{1}{2} {\text{base}} = 1.6 {\text{ seen}}\) (M1)
award (M1) for halving base
\({\text{OC}}^2 = 1.6^2 + 1.6^2 = 5.12\) (A1)
award (A1) for one correct use of Pythagoras
\(5.12 + 2.8^2 = 12.96 = {\text{VC}}^2\) (M1)
award (M1) for using Pythagoras again to find VC2
VC = 3.6 AG
award (A1) for 3.6 obtained from 12.96 only (not 12.95…) (A1)
OR
\({\text{AC}}^2 = 3.2^2 + 3.2^2 = 20.48\) (A1)
award (A1) for one correct use of Pythagoras
({\text{OC}} = \frac{1}{2} \sqrt{20.48}\) ( = 2.26…) (M1)
award (M1) for halving AC
\(2.8^2 + (2.26…)^2 = {\text{VC}}^2 = 12.96\) (M1)
award (M1) for using Pythagoras again to find VC2
VC = 3.6 AG (A1)
award (A1) for 3.6 obtained from 12.96 only (not 12.95…)[4 marks]
\(3.2^2 = 3.6^2 + 3.6^2 – 2 \times (3.6) (3.6) \cos\) \({\text{B}}{\operatorname {\hat V}}{\text{C}}\) (M1)(A1)
\({\text{B}}{\operatorname {\hat V}}{\text{C}}\) \( = {52.8^\circ }\) (no (ft) here) (A1)(G2)
award (M1) for substituting in correct formula, (A1) for correct substitution
OR
\(\sin\) \({\text{B}}{\operatorname {\hat V}}{\text{M}}\) \( = \frac{{1.6}}{{3.6}}\) where M is the midpoint of BC (M1)(A1)
\({\text{B}}{\operatorname {\hat V}}{\text{C}}\) \( = {52.8^\circ}\) (no (ft) here) (A1)[3 marks]
Unit penalty (UP) is applicable in question parts (a), (b) and (e) only.
\(4 \times \frac{1}{2}{(3.6)^2} \times \sin (52.8^\circ ) + {(3.2)^2}\) (M1)(M1)(M1)
award (M1) for \( \times 4\), (M1) for substitution in relevant triangle area, (\(\frac{1}{2}(3.2)(2.8)\) gets (M0))
(M1) for \(+ {(3.2)^2}\)
(UP) = 30.9 cm2 ((ft) from their (d)) (A1)(ft)(G2)[4 marks]
Question
A farmer has a triangular field, ABC, as shown in the diagram.
AB = 35 m, BC = 80 m and BÂC = 105°, and D is the midpoint of BC.
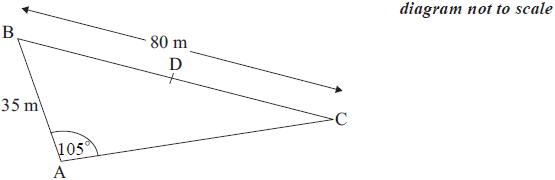
Find the size of BĈA.[3]
Calculate the length of AD.[5]
The farmer wants to build a fence around ABD.
Calculate the total length of the fence.[2]
The farmer wants to build a fence around ABD.
The farmer pays 802.50 USD for the fence. Find the cost per metre.[2]
Calculate the area of the triangle ABD.[3]
A layer of earth 3 cm thick is removed from ABD. Find the volume removed in cubic metres.[3]
Answer/Explanation
Markscheme
\(\frac{{\sin {\text{BCA}}}}{{35}} = \frac{{\sin 105^\circ }}{{80}}\) (M1)(A1)
Note: Award (M1) for correct substituted formula, (A1) for correct substitutions.
\({\text{B}}{\operatorname{\hat C}}{\text{A}} = 25.0^{\circ}\) (A1)(G2)[3 marks]
Note: Unit penalty (UP) applies in parts (b)(c) and (e)
Length BD = 40 m (A1)
Angle ABC = 180° − 105° − 25° = 50° (A1)(ft)
Note: (ft) from their answer to (a).
AD2 = 352 + 402 − (2 × 35 × 40 × cos 50°) (M1)(A1)(ft)
Note: Award (M1) for correct substituted formula, (A1)(ft) for correct substitutions.
(UP) AD = 32.0 m (A1)(ft)(G3)
Notes: If 80 is used for BD award at most (A0)(A1)(ft)(M1)(A1)(ft)(A1)(ft) for an answer of 63.4 m.
If the angle ABC is incorrectly calculated in this part award at most (A1)(A0)(M1)(A1)(ft)(A1)(ft).
If angle BCA is used award at most (A1)(A0)(M1)(A0)(A0).[5 marks]
Note: Unit penalty (UP) applies in parts (b)(c) and (e)
length of fence = 35 + 40 + 32 (M1)
(UP) = 107 m (A1)(ft)(G2)
Note: (M1) for adding 35 + 40 + their (b).[2 marks]
cost per metre \( = \frac{802.50}{107}\) (M1)
Note: Award (M1) for dividing 802.50 by their (c).
cost per metre = 7.50 USD (7.5 USD) (USD not required) (A1)(ft)(G2)[2 marks]
Note: Unit penalty (UP) applies in parts (b)(c) and (e)
Area of ABD \( = \frac{1}{2} \times 35 \times 40 \times \sin 50^\circ \) (M1)
= 536.2311102 (A1)(ft)
(UP) = 536 m2 (A1)(ft)(G2)
Note: Award (M1) for correct substituted formula, (A1)(ft) for correct substitution, (ft) from their value of BD and their angle ABC in (b).[3 marks]
Volume = 0.03 × 536 (A1)(M1)
= 16.08
= 16.1 (A1)(ft)(G2)
Note: Award (A1) for 0.03, (M1) for correct formula. (ft) from their (e).
If 3 is used award at most (A0)(M1)(A0).[3 marks]
Question
The diagram shows an office tower of total height 126 metres. It consists of a square based pyramid VABCD on top of a cuboid ABCDPQRS.
V is directly above the centre of the base of the office tower.
The length of the sloping edge VC is 22.5 metres and the angle that VC makes with the base ABCD (angle VCA) is 53.1°.
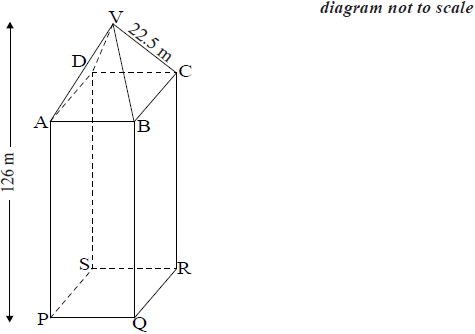
Write down the length of VA in metres.[1]
Sketch the triangle VCA showing clearly the length of VC and the size of angle VCA.[1]
Show that the height of the pyramid is 18.0 metres correct to 3 significant figures.[2]
Calculate the length of AC in metres.[3]
Show that the length of BC is 19.1 metres correct to 3 significant figures.[2]
Calculate the volume of the tower.[4]
To calculate the cost of air conditioning, engineers must estimate the weight of air in the tower. They estimate that 90 % of the volume of the tower is occupied by air and they know that 1 m3 of air weighs 1.2 kg.
Calculate the weight of air in the tower.[3]
Answer/Explanation
Markscheme
22.5 (m) (A1)[1 mark]
[1 mark](A1)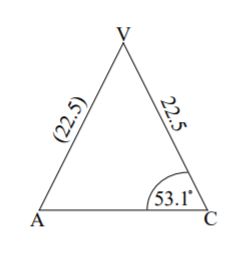
h = 22.5 sin 53.1° (M1)
= 17.99 (A1)
= 18.0 (AG)
Note: Unrounded answer must be seen for (A1) to be awarded.
Accept 18 as (AG).[2 marks]
\({\text{AC}} = 2\sqrt {{{22.5}^2} – {{17.99…}^2}} \) (M1)(M1)
Note: Award (M1) for multiplying by 2, (M1) for correct substitution into formula.
OR
AC = 2(22.5)cos53.1° (M1)(M1)
Notes: Award (M1) for correct use of cosine trig ratio, (M1) for multiplying by 2.
OR
AC2 = 22.52 + 22.52 – 2(22.5)(22.5) cos73.8° (M1)(A1)
Note: Award (M1) for substituted cosine formula, (A1) for correct substitutions.
OR
\(\frac{{{\text{AC}}}}{{\sin (73.8^\circ )}} = \frac{{22.5}}{{\sin (53.1^\circ )}}\) (M1)(A1)
Note: Award (M1) for substituted sine formula, (A1) for correct substitutions.
AC = 27.0 (A1)(G2)[3 marks]
\({\text{BC}} = \sqrt {{{13.5}^2} + {{13.5}^2}} \) (M1)
= 19.09 (A1)
= 19.1 (AG)
OR
x2 + x2 = 272 (M1)
2x2 = 272 (A1)
BC = 19.09… (A1)
= 19.1 (AG)
Notes: Unrounded answer must be seen for (A1) to be awarded.[2 marks]
Volume = Pyramid + Cuboid
\( = \frac{1}{3}(18)({19.1^2}) + (108)({19.1^2})\) (A1)(M1)(M1)
Note: Award (A1) for 108, the height of the cuboid seen. Award (M1) for correctly substituted volume of cuboid and (M1) for correctly substituted volume of pyramid.
= \(41\,588\) (41\(\,\)553 if 2(13.52) is used)
= \(41\,600\) m3 (A1)(ft)(G3)[4 marks]
Weight of air = \(41\,600 \times 1.2 \times 0.9\) (M1)(M1)
= \(44\,900{\text{ kg}}\) (A1)(ft)(G2)
Note: Award (M1) for their part (e) × 1.2, (M1) for × 0.9.
Award at most (M1)(M1)(A0) if the volume of the cuboid is used.[3 marks]
Question
In the diagram below A, B and C represent three villages and the line segments AB, BC and CA represent the roads joining them. The lengths of AC and CB are 10 km and 8 km respectively and the size of the angle between them is 150°.
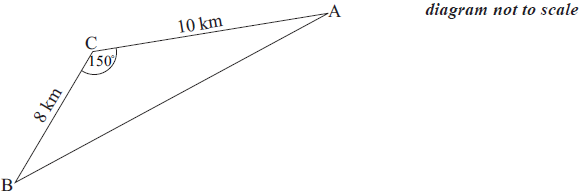
Find the length of the road AB.[3]
Find the size of the angle CAB.[3]
Village D is halfway between A and B. A new road perpendicular to AB and passing through D is built. Let T be the point where this road cuts AC. This information is shown in the diagram below.
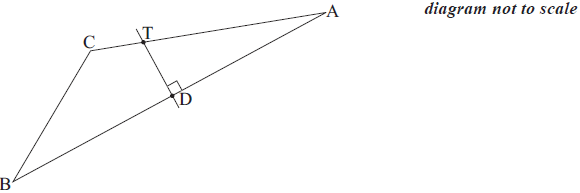
Write down the distance from A to D.[1]
Show that the distance from D to T is 2.06 km correct to three significant figures.[2]
A bus starts and ends its journey at A taking the route AD to DT to TA.
Find the total distance for this journey.[3]
The average speed of the bus while it is moving on the road is 70 km h–1. The bus stops for 5 minutes at each of D and T .
Estimate the time taken by the bus to complete its journey. Give your answer correct to the nearest minute.[4]
Answer/Explanation
Markscheme
AB2 = 102 + 82 – 2 × 10 × 8 × cos150° (M1)(A1)
AB = 17.4 km (A1)(G2)
Note: Award (M1) for substitution into correct formula, (A1) for correct substitution, (A1) for correct answer.[3 marks]
\(\frac{8}{{\sin {\text{C}}\hat {\rm A}{\text{B}}}} = \frac{{17.4}}{{\sin 150^\circ }}\) (M1)(A1)
\({\text{C}}\hat {\rm A}{\text{B}} = 13.3^\circ \) (A1)(ft)(G2)
Notes: Award (M1) for substitution into correct formula, (A1) for correct substitution, (A1) for correct answer. Follow through from their answer to part (a).[3 marks]
AD = 8.70 km (8.7 km) (A1)(ft)
Note: Follow through from their answer to part (a).[1 mark]
DT = tan (13.29…°) × 8.697… = 2.0550… (M1)(A1)
= 2.06 (AG)
Notes: Award (M1) for correct substitution in the correct formula, award (A1) for the unrounded answer seen. If 2.06 not seen award at most (M1)(AO).[2 marks]
\(\sqrt {{{8.70}^2} + {{2.06}^2}} + 8.70 + 2.06\) (A1)(M1)
= 19.7 km (A1)(ft)(G2)
Note: Award (A1) for AT, (M1) for adding the three sides of the triangle ADT, (A1)(ft) for answer. Follow through from their answer to part (c).[3 marks]
\(\frac{{19.7}}{{70}} \times 60 + 10\) (M1)(M1)
= 26.9 (A1)(ft)
Note: Award (M1) for time on road in minutes, (M1) for adding 10, (A1)(ft) for unrounded answer. Follow through from their answer to (e).
= 27 (nearest minute) (A1)(ft)(G3)
Note: Award (A1)(ft) for their unrounded answer given to the nearest minute.[4 marks]
Question
The diagram shows a Ferris wheel that moves with constant speed and completes a rotation every 40 seconds. The wheel has a radius of \(12\) m and its lowest point is \(2\) m above the ground.
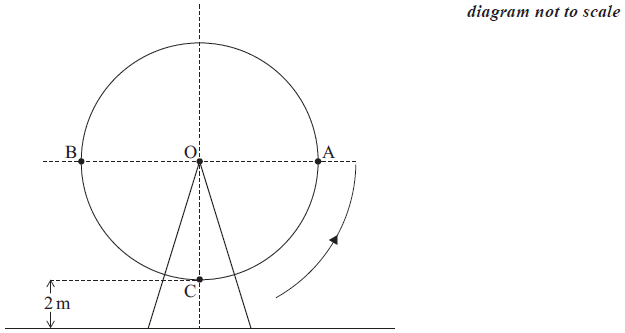
Initially, a seat C is vertically below the centre of the wheel, O. It then rotates in an anticlockwise (counterclockwise) direction.
Write down
(i) the height of O above the ground;
(ii) the maximum height above the ground reached by C .[2]
In a revolution, C reaches points A and B , which are at the same height above the ground as the centre of the wheel. Write down the number of seconds taken for C to first reach A and then B .[2]
The sketch below shows the graph of the function, \(h(t)\) , for the height above ground of C, where \(h\) is measured in metres and \(t\) is the time in seconds, \(0 \leqslant t \leqslant 40\) .
Copy the sketch and show the results of part (a) and part (b) on your diagram. Label the points clearly with their coordinates.[4]
Answer/Explanation
Markscheme
(i) \(14\) m (A1)
(ii) \(26\) m (A1)[2 marks]
A:\(10\), B:\(30\) (A1)(A1)[2 marks]
 (A1)(ft)(A1)(ft)(A1)(ft)(A1)(ft)
(A1)(ft)(A1)(ft)(A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for coordinates of each point clearly indicated either by scale or by coordinate pairs. Points need not be labelled A and B in the second diagram. Award a maximum of (A1)(A0)(A1)(ft)(A1)(ft) if coordinates are reversed. Do not penalise reversed coordinates if this has already been penalised in Q4(a)(iii).[4 marks]
Question
A cross-country running course consists of a beach section and a forest section. Competitors run from \({\text{A}}\) to \({\text{B}}\), then from \({\text{B}}\) to \({\text{C}}\) and from \({\text{C}}\) back to \({\text{A}}\).
The running course from \({\text{A}}\) to \({\text{B}}\) is along the beach, while the course from \({\text{B}}\), through \({\text{C}}\) and back to \({\text{A}}\), is through the forest.
The course is shown on the following diagram.
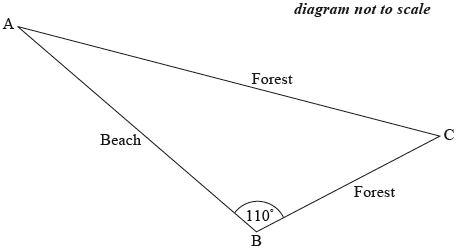
Angle \({\text{ABC}}\) is \(110^\circ\).
It takes Sarah \(5\) minutes and \(20\) seconds to run from \({\text{A}}\) to \({\text{B}}\) at a speed of \(3.8{\text{ m}}{{\text{s}}^{ – 1}}\).
Using ‘distance = speed \( \times \) time’, show that the distance from \({\text{A}}\) to \({\text{B}}\) is \(1220\) metres correct to 3 significant figures.[2]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the speed, in \({\text{m}}{{\text{s}}^{ – 1}}\), that Sarah runs from \({\text{B}}\) to \({\text{C}}\).[1]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the distance, in metres, from \({\mathbf{C}}\) to \({\mathbf{A}}\).[3]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the total distance, in metres, of the cross-country running course.[2]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Find the size of angle \({\text{BCA}}\).[3]
The distance from \({\text{B}}\) to \({\text{C}}\) is \(850\) metres. Running this part of the course takes Sarah \(5\) minutes and \(3\) seconds.
Calculate the area of the cross-country course bounded by the lines \({\text{AB}}\), \({\text{BC}}\) and \({\text{CA}}\).[3]
Answer/Explanation
Markscheme
\(3.8 \times 320\) (A1)
Note: Award (A1) for \(320\) or equivalent seen.
\( = 1216\) (A1)
\( = 1220{\text{ (m)}}\) (AG)
Note: Both unrounded and rounded answer must be seen for the final (A1) to be awarded.[2 marks]
\(\frac{{850}}{{303}}{\text{ (m}}{{\text{s}}^{ – 1}}){\text{ (2.81, 2.80528}} \ldots {\text{)}}\) (A1)(G1)[1 mark]
\({\text{A}}{{\text{C}}^2} = {1220^2} + {850^2} – 2(1220)(850)\cos 110^\circ \) (M1)(A1)
Note: Award (M1) for substitution into cosine rule formula, (A1) for correct substitutions.
\({\text{AC}} = 1710{\text{ (m) (1708.87}} \ldots {\text{)}}\) (A1)(G2)
Notes: Accept \(1705{\text{ }} (1705.33…)\).[3 marks]
\(1220 + 850 + {\text{1708.87}} \ldots \) (M1)
\( = {\text{3780 (m) (3778.87}} \ldots {\text{)}}\) (A1)(ft)(G1)
Notes: Award (M1) for adding the three sides. Follow through from their answer to part (c). Accept \(3771{\text{ }} (3771.33…)\).[2 marks]
\(\frac{{\sin C}}{{1220}} = \frac{{\sin 110^\circ }}{{{\text{1708.87}} \ldots }}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into sine rule formula, (A1)(ft) for correct substitutions. Follow through from their part (c).
\(C = 42.1^\circ {\text{ (42.1339}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Accept \(41.9^{\circ}, 42.0^{\circ}, 42.2^{\circ}, 42.3^{\circ}\).
OR
\(\cos C = \frac{{{\text{1708.87}}{ \ldots ^2} + {{850}^2} – {{1220}^2}}}{{2 \times {\text{1708.87}} \ldots \times 850}}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into cosine rule formula, (A1)(ft) for correct substitutions. Follow through from their part (c).
\(C = 42.1^\circ {\text{ (42.1339}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Accept \(41.2^{\circ}, 41.8^{\circ}, 42.4^{\circ}\).[3 marks]
\(\frac{1}{2} \times 1220 \times 850 \times \sin 110^\circ \) (M1)(A1)(ft)
OR
\(\frac{1}{2} \times {\text{1708.87}} \ldots \times 850 \times \sin {\text{42.1339}} \ldots ^\circ \) (M1)(A1)(ft)
OR
\(\frac{1}{2} \times 1220 \times {\text{1708.87}} \ldots \times \sin {\text{27.8661}} \ldots ^\circ \) (M1)(A1)(ft)
Note: Award (M1) for substitution into area formula, (A1)(ft) for correct substitution.
\( = 487\,000{\text{ }}{{\text{m}}^2}{\text{ (487}}\,{\text{230}} \ldots {\text{ }}{{\text{m}}^2})\) (A1)(ft)(G2)
Notes: The answer is \(487\,000{\text{ }}{{\text{m}}^2}\), units are required.
Accept \(486\,000{\text{ }}{{\text{m}}^2}{\text{ (485}}\,{\text{633}} \ldots {\text{ }}{{\text{m}}^2})\).
If workings are not shown and units omitted, award (G1) for \(487\,000{\text{ or }}486\,000\).
Follow through from parts (c) and (e).[3 marks]
Question
A boat race takes place around a triangular course, \({\text{ABC}}\), with \({\text{AB}} = 700{\text{ m}}\), \({\text{BC}} = 900{\text{ m}}\) and angle \({\text{ABC}} = 110^\circ \). The race starts and finishes at point \({\text{A}}\).
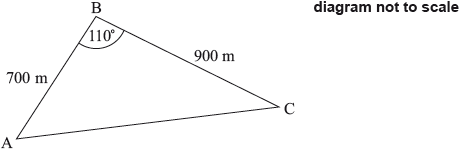
Calculate the total length of the course.[4]
It is estimated that the fastest boat in the race can travel at an average speed of \(1.5\;{\text{m}}\,{{\text{s}}^{ – 1}}\).
Calculate an estimate of the winning time of the race. Give your answer to the nearest minute.[3]
It is estimated that the fastest boat in the race can travel at an average speed of \(1.5\;{\text{m}}\,{{\text{s}}^{ – 1}}\).
Find the size of angle \({\text{ACB}}\).[3]
To comply with safety regulations, the area inside the triangular course must be kept clear of other boats, and the shortest distance from \({\text{B}}\) to \({\text{AC}}\) must be greater than \(375\) metres.
Calculate the area that must be kept clear of boats.[3]
To comply with safety regulations, the area inside the triangular course must be kept clear of other boats, and the shortest distance from \({\text{B}}\) to \({\text{AC}}\) must be greater than \(375\) metres.
Determine, giving a reason, whether the course complies with the safety regulations.[3]
The race is filmed from a helicopter, \({\text{H}}\), which is flying vertically above point \({\text{A}}\).
The angle of elevation of \({\text{H}}\) from \({\text{B}}\) is \(15^\circ\).
Calculate the vertical height, \({\text{AH}}\), of the helicopter above \({\text{A}}\).[2]
The race is filmed from a helicopter, \({\text{H}}\), which is flying vertically above point \({\text{A}}\).
The angle of elevation of \({\text{H}}\) from \({\text{B}}\) is \(15^\circ\).
Calculate the maximum possible distance from the helicopter to a boat on the course.[3]
Answer/Explanation
Markscheme
\({\text{A}}{{\text{C}}^2} = {700^2} + {900^2} – 2 \times 700 \times 900 \times \cos 110^\circ \) (M1)(A1)
\({\text{AC}} = 1315.65 \ldots \) (A1)(G2)
length of course \( = 2920{\text{ (m)}}\;\;\;(2915.65 \ldots {\text{ m)}}\) (A1)
Notes: Award (M1) for substitution into cosine rule formula, (A1) for correct substitution, (A1) for correct answer.
Award (G3) for \(2920\;\;\;(2915.65 \ldots )\) seen without working.
The final (A1) is awarded for adding \(900\) and \(700\) to their \({\text{AC}}\) irrespective of working seen.
\(\frac{{2915.65}}{{1.5}}\) (M1)
Note: Award (M1) for their length of course divided by \(1.5\).
Follow through from part (a).
\( = 1943.76 \ldots {\text{ (seconds)}}\) (A1)(ft)
\( = 32{\text{ (minutes)}}\) (A1)(ft)(G2)
Notes: Award the final (A1) for correct conversion of their answer in seconds to minutes, correct to the nearest minute.
Follow through from part (a).
\(\frac{{700}}{{\sin {\text{ACB}}}} = \frac{{1315.65 \ldots }}{{\sin 110^\circ }}\) (M1)(A1)(ft)
OR
\(\cos {\text{ACB}} = \frac{{{{900}^2} + 1315.65{ \ldots ^2} – {{700}^2}}}{{2 \times 900 \times 1315.65 \ldots }}\) (M1)(A1)(ft)
\({\text{ACB}} = 30.0^\circ \;\;\;(29.9979 \ldots ^\circ )\) (A1)(ft)(G2)
Notes: Award (M1) for substitution into sine rule or cosine rule formula, (A1) for their correct substitution, (A1) for correct answer.
Accept \(29.9^\circ\) for sine rule and \(29.8^\circ\) for cosine rule from use of correct three significant figure values. Follow through from their answer to (a).
\(\frac{1}{2} \times 700 \times 900 \times \sin 110^\circ \) (M1)(A1)
Note: Accept \(\frac{1}{2} \times {\text{their AC}} \times {\text{900}} \times {\text{sin(their ACB)}}\). Follow through from parts (a) and (c).
\( = 296000{\text{ }}{{\text{m}}^2}\;\;\;(296003{\text{ }}{{\text{m}}^2})\) (A1)(G2)
Notes: Award (M1) for substitution into area of triangle formula, (A1) for correct substitution, (A1) for correct answer.
Award (G1) if \(296000\) is seen without units or working.
\(\sin 29.9979 \ldots = \frac{{{\text{distance}}}}{{900}}\) (M1)
\({\text{(distance}} = ){\text{ }}450{\text{ (m)}}\;\;\;{\text{(449.971}} \ldots {\text{)}}\) (A1)(ft)(G2)
Note: Follow through from part (c).
OR
\(\frac{1}{2} \times {\text{distance}} \times 1315.65 \ldots = 296003\) (M1)
\(({\text{distance}} = ){\text{ }}450{\text{ (m)}}\;\;\;{\text{(449.971}} \ldots {\text{)}}\) (A1)(ft)(G2)
Note: Follow through from part (a) and part (d).
\(450\) is greater than \(375\), thus the course complies with the safety regulations (R1)
Notes: A comparison of their area from (d) and the area resulting from the use of \(375\) as the perpendicular distance is a valid approach and should be given full credit. Similarly a comparison of angle \({\text{ACB}}\) and \({\sin ^{ – 1}}\left( {\frac{{375}}{{900}}} \right)\) should be given full credit.
Award (R0) for correct answer without any working seen. Award (R1)(ft) for a justified reason consistent with their working.
Do not award (M0)(A0)(R1).
\(\tan 15^\circ = \frac{{{\text{AH}}}}{{700}}\) (M1)
Note: Award (M1) for correct substitution into trig formula.
\({\text{AH}} = 188{\text{ (m)}}\;\;\;(187.564 \ldots )\) (A1)(ft)(G2)
\({\text{H}}{{\text{C}}^2} = 187.564{ \ldots ^2} + 1315.65{ \ldots ^2}\) (M1)(A1)
Note: Award (M1) for substitution into Pythagoras, (A1) for their \(1315.65{ \ldots}\) and their \(187.564{ \ldots}\) correctly substituted in formula.
\({\text{HC}} = 1330 \ldots {\text{ (m)}}\;\;\;(1328.95 \ldots )\) (A1)(ft)(G2)
Note: Follow through from their answer to parts (a) and (f).
Question
The following diagram shows a perfume bottle made up of a cylinder and a cone.
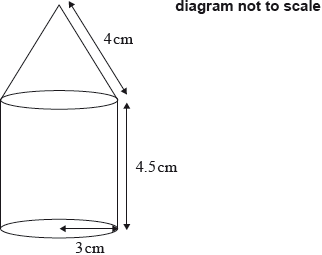
The radius of both the cylinder and the base of the cone is 3 cm.
The height of the cylinder is 4.5 cm.
The slant height of the cone is 4 cm.
(i) Show that the vertical height of the cone is \(2.65\) cm correct to three significant figures.
(ii) Calculate the volume of the perfume bottle.[6]
The bottle contains \({\text{125 c}}{{\text{m}}^{\text{3}}}\) of perfume. The bottle is not full and all of the perfume is in the cylinder part.
Find the height of the perfume in the bottle.[2]
Temi makes some crafts with perfume bottles, like the one above, once they are empty. Temi wants to know the surface area of one perfume bottle.
Find the total surface area of the perfume bottle.[4]
Temi covers the perfume bottles with a paint that costs 3 South African rand (ZAR) per millilitre. One millilitre of this paint covers an area of \({\text{7 c}}{{\text{m}}^{\text{2}}}\).
Calculate the cost, in ZAR, of painting the perfume bottle. Give your answer correct to two decimal places.[4]
Temi sells her perfume bottles in a craft fair for 325 ZAR each. Dominique from France buys one and wants to know how much she has spent, in euros (EUR). The exchange rate is 1 EUR = 13.03 ZAR.
Find the price, in EUR, that Dominique paid for the perfume bottle. Give your answer correct to two decimal places.[2]
Answer/Explanation
Markscheme
(i) \({x^2} + {3^2} = {4^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
Accept correct alternative method using trigonometric ratios.
\(x = 2.64575 \ldots \) (A1)
\(x = 2.65{\text{ }}({\text{cm}})\) (AG)
Note: The unrounded and rounded answer must be seen for the (A1) to be awarded.
OR
\(\sqrt {{4^2} – {3^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ formula.
\( = \sqrt 7 \) (A1)
\( = 2.65{\text{ (cm)}}\) (AG)
Note: The exact answer must be seen for the final (A1) to be awarded.
(ii) \(\pi \times {3^2} \times 4.5 + \frac{1}{3}\pi \times {3^2} \times 2.65\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula, (M1) for correct substitution into the volume of a cone formula, (M1) for adding both of their volumes.
\( = 152{\text{ c}}{{\text{m}}^3}\;\;\;(152.210 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}48.45\pi {\text{ c}}{{\text{m}}^3})\) (A1)(G3)
\(\pi {3^2}h = 125\) (M1)
Note: Award (M1) for correct substitution into the volume of a cylinder formula.
Accept alternative methods. Accept \(4.43\) (\(4.42913 \ldots \)) from using rounded answers in \(h = \frac{{125 \times 4.5}}{{127}}\).
\(h = 4.42{\text{ (cm)}}\;\;\;\left( {4.42097 \ldots {\text{ (cm)}}} \right)\) (A1)(G2)
\(2\pi \times 3 \times 4.5 + \pi \times 3 \times 4 + \pi \times {3^2}\) (M1)(M1)(M1)
Note: Award (M1) for correct substitution into curved surface area of a cylinder formula, (M1) for correct substitution into the curved surface area of a cone formula, (M1) for adding the area of the base of the cylinder to the other two areas.
\( = 151{\text{ c}}{{\text{m}}^2}\;\;\;(150.796 \ldots {\text{ c}}{{\text{m}}^2},{\text{ }}48\pi {\text{ c}}{{\text{m}}^2})\) (A1)(G3)
\(\frac{{150.796 \ldots }}{7} \times 3\) (M1)(M1)
Notes: Award (M1) for dividing their answer to (c) by \(7\), (M1) for multiplying by \(3\). Accept equivalent methods.
\( = 64.63{\text{ (ZAR)}}\) (A1)(ft)(G2)
Notes: The (A1) is awarded for their correct answer, correctly rounded to 2 decimal places. Follow through from their answer to part (c). If rounded answer to part (c) is used the answer is \(64.71\) (ZAR).
\(\frac{{325}}{{13.03}}\) (M1)
Note: Award (M1) for dividing \(325\) by \(13.03\).
\( = 24.94{\text{ (EUR)}}\) (A1)(G2)
Note: The (A1) is awarded for the correct answer rounded to 2 decimal places, unless already penalized in part (d).
Question
For an ecological study, Ernesto measured the average concentration \((y)\) of the fine dust, \({\text{PM}}10\), in the air at different distances \((x)\) from a power plant. His data are represented on the following scatter diagram. The concentration of \({\text{PM}}10\) is measured in micrograms per cubic metre and the distance is measured in kilometres.
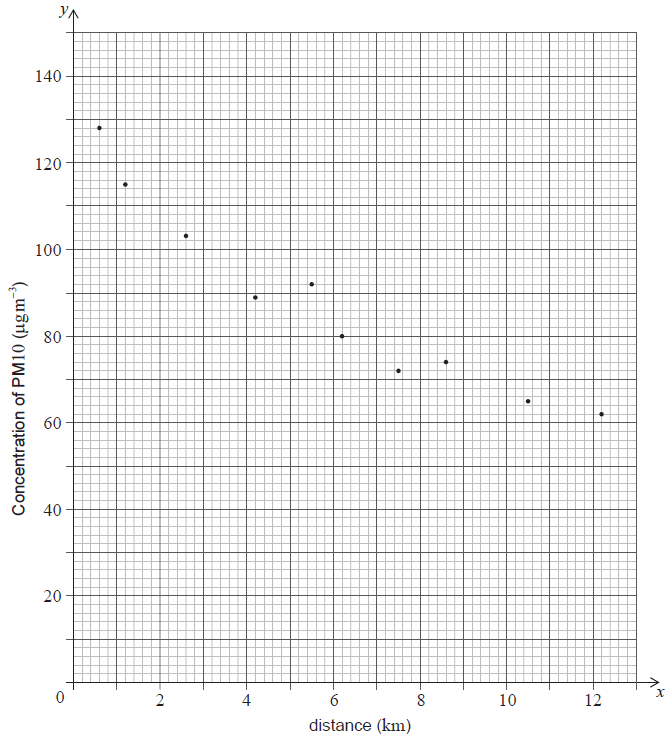
His data are also listed in the following table.

Use the scatter diagram to find the value of \(a\) and of \(b\) in the table.[2]
Calculate
i) \({\bar x}\) , the mean distance from the power plant;
ii) \({\bar y}\) , the mean concentration of \({\text{PM}}10\) ;
iii) \(r\) , the Pearson’s product–moment correlation coefficient.[4]
Write down the equation of the regression line \(y\) on \(x\) .[2]
Ernesto’s school is located \(14\,{\text{km}}\) from the power plant. He uses the equation of the regression line to estimate the concentration of \({\text{PM}}10\) in the air at his school.
i) Calculate the value of Ernesto’s estimate.
ii) State whether Ernesto’s estimate is reliable. Justify your answer.[4]
Answer/Explanation
Markscheme
\(a = 4.2\,;\,\,b = 74\) (A1)(A1)
i) \(5.91\,({\text{km}})\) (A1)(ft)
ii) \(88\) (micrograms per cubic metre) (A1)(ft)
Note: Follow through from part (a) irrespective of working seen.
iii) \( – 0.956\,\,\,\,( – 0.955528…)\) (G2)(ft)
Note: Follow through from part (a) irrespective of working seen.
\(y = – 5.39x + 120\,\,\,\,(y = – 5.38955…x + 119.852…)\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for \( – 5.39\). Award (A1)(ft) for \(120\). If answer is not an equation award at most (A1)(ft)(A0). Follow through from part (a) irrespective of working seen.
i) \( – 5.38955… \times 14 + 119.852…\) (M1)
Note: Award (M1) for correct substitution into their regression line.
\( = 44.4\,\,(44.3984…)\) (A1)(ft)(G2)
Note: Follow through from part (c). Accept \(44.5\,\,(44.54)\) from use of \(3\) significant figure values.
ii) Ernesto’s estimate is not reliable (A1)
this is extrapolation (R1)
OR
\(14\,{\text{km}}\) is not within the range (outside the domain) of distances given (R1)
Note: Do not accept “\(14\) is too high” or “\(14\) is an outlier” or “result not valid/not reliable” if explanation not given. Do not award (A1)(R0). Do not accept reasoning based on the strength of \(r\).
Question
A distress flare is fired into the air from a ship at sea. The height, \(h\) , in metres, of the flare above sea level is modelled by the quadratic function
\[h\,(t) = – 0.2{t^2} + 16t + 12\,,\,t \geqslant 0\,,\]
where \(t\) is the time, in seconds, and \(t = 0\,\) at the moment the flare was fired.
Write down the height from which the flare was fired.[1]
Find the height of the flare \(15\) seconds after it was fired.[2]
The flare fell into the sea \(k\) seconds after it was fired.
Find the value of \(k\) .[2]
Find \(h’\,(t)\,.\)[2]
i) Show that the flare reached its maximum height \(40\) seconds after being fired.
ii) Calculate the maximum height reached by the flare.[3]
The nearest coastguard can see the flare when its height is more than \(40\) metres above sea level.
Determine the total length of time the flare can be seen by the coastguard.[3]
Answer/Explanation
Markscheme
\(12\,({\text{m}})\) (A1)
\((h\,(15) = ) – 0.2 \times {15^2} + 16 \times 15 + 12\) (M1)
Note: Award (M1) for substitution of \(15\) in expression for \(h\).
\( = 207\,({\text{m}})\) (A1)(G2)
\(h\,(k) = 0\) (M1)
Note: Award (M1) for setting \(h\) to zero.
\((k = )\,\,\,80.7\,({\text{s}})\,\,\,(80.7430)\) (A1)(G2)
Note: Award at most (M1)(A0) for an answer including \(K = – 0.743\) .
Award (A0) for an answer of \(80\) without working.
\(h’\,(t) = – 0.4t + 16\) (A1)(A1)
Note: Award (A1) for \( – 0.4t\), (A1) for \(16\). Award at most (A1)(A0) if extra terms seen. Do not accept \(x\) for \(t\).
i) \( – 0.4t + 16 = 0\) (M1)
Note: Award (M1) for setting their derivative, from part (d), to zero, provided the correct conclusion is stated and consistent with their \(h’\,(t)\).
OR
\(t = \frac{{ – 16}}{{2 \times ( – 0.2)}}\) (M1)
Note: Award (M1) for correct substitution into axis of symmetry formula, provided the correct conclusion is stated.
\(t = \,\,40\,({\text{s}})\) (AG)
ii) \( – 0.2 \times {40^2} + 16 \times 40 + 12\) (M1)
Note: Award (M1) for substitution of \(40\) in expression for \(h\).
\( = 332\,({\text{m}})\) (A1)(G2)
\(h\,(t) = 40\) (M1)
Note: Award (M1) for setting \(h\) to \(40\). Accept inequality sign.
OR
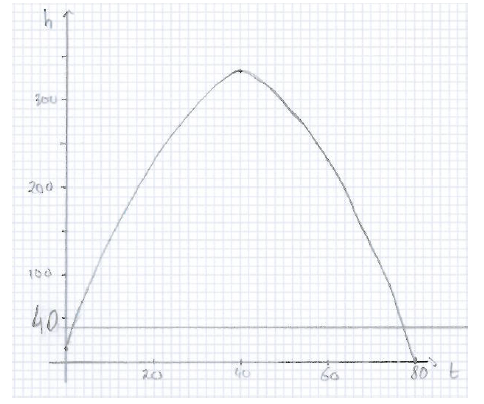
M1
Note: Award (M1) for correct sketch. Indication of scale is not required.
\(78.2 – 1.17\,\,(78.2099…\,\, – 1.79005…)\) (A1)
Note: Award (A1) for \(1.79\) and \(78.2\) seen.
(total time \( = \)) \(76.4\,({\text{s}})\,\,\,(76.4198…)\) (A1)(G2)
Note: Award (G1) if the two endpoints are given as the final answer with no working.
Question
The Great Pyramid of Giza in Egypt is a right pyramid with a square base. The pyramid is made of solid stone. The sides of the base are \(230\,{\text{m}}\) long. The diagram below represents this pyramid, labelled \({\text{VABCD}}\).
\({\text{V}}\) is the vertex of the pyramid. \({\text{O}}\) is the centre of the base, \({\text{ABCD}}\) . \({\text{M}}\) is the midpoint of \({\text{AB}}\). Angle \({\text{ABV}} = 58.3^\circ \) .
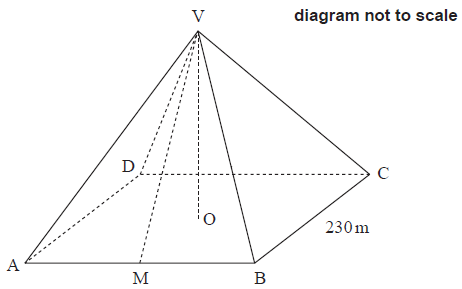
Show that the length of \({\text{VM}}\) is \(186\) metres, correct to three significant figures.[3]
Calculate the height of the pyramid, \({\text{VO}}\) .[2]
Find the volume of the pyramid.[2]
Write down your answer to part (c) in the form \(a \times {10^k}\) where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\) .[2]
Ahmad is a tour guide at the Great Pyramid of Giza. He claims that the amount of stone used to build the pyramid could build a wall \(5\) metres high and \(1\) metre wide stretching from Paris to Amsterdam, which are \(430\,{\text{km}}\) apart.
Determine whether Ahmad’s claim is correct. Give a reason.[4]
Ahmad and his friends like to sit in the pyramid’s shadow, \({\text{ABW}}\), to cool down.
At mid-afternoon, \({\text{BW}} = 160\,{\text{m}}\) and angle \({\text{ABW}} = 15^\circ .\)
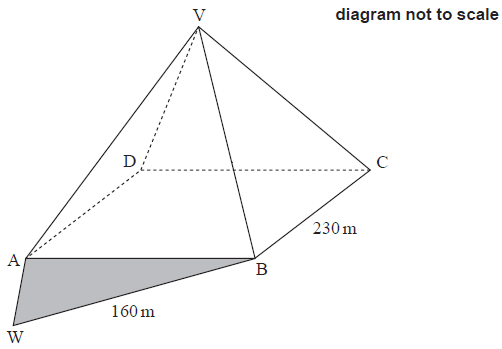
i) Calculate the length of \({\text{AW}}\) at mid-afternoon.
ii) Calculate the area of the shadow, \({\text{ABW}}\), at mid-afternoon.[6]
Answer/Explanation
Markscheme
\(\tan \,(58.3) = \frac{{{\text{VM}}}}{{115}}\) OR \(115 \times \tan \,(58.3^\circ )\) (A1)(M1)
Note: Award (A1) for \(115\,\,\left( {ie\,\frac{{230}}{2}} \right)\) seen, (M1) for correct substitution into trig formula.
\(\left( {{\text{VM}} = } \right)\,\,186.200\,({\text{m}})\) (A1)
\(\left( {{\text{VM}} = } \right)\,\,186\,({\text{m}})\) (AG)
Note: Both the rounded and unrounded answer must be seen for the final (A1) to be awarded.
\({\text{V}}{{\text{O}}^2} + {115^2} = {186^2}\) OR \(\sqrt {{{186}^2} – {{115}^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras formula. Accept alternative methods.
\({\text{(VO}} = )\,\,146\,({\text{m}})\,\,(146.188…)\) (A1)(G2)
Note: Use of full calculator display for \({\text{VM}}\) gives \(146.443…\,{\text{(m)}}\).
Units are required in part (c)
\(\frac{1}{3}({230^2} \times 146.188…)\) (M1)
Note: Award (M1) for correct substitution in volume formula. Follow through from part (b).
\( = 2\,580\,000\,{{\text{m}}^3}\,\,(2\,577\,785…\,{{\text{m}}^3})\) (A1)(ft)(G2)
Note: The answer is \(2\,580\,000\,{{\text{m}}^3}\) , the units are required. Use of \({\text{OV}} = 146.442\) gives \(2582271…\,{{\text{m}}^3}\)
Use of \({\text{OV}} = 146\) gives \(2574466…\,{{\text{m}}^3}.\)
\(2.58 \times {10^6}\,({{\text{m}}^3})\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for \(2.58\) and (A1)(ft) for \( \times {10^6}.\,\)
Award (A0)(A0) for answers of the type: \(2.58 \times {10^5}\,({{\text{m}}^3}).\)
Follow through from part (c).
the volume of a wall would be \(430\,000 \times 5 \times 1\) (M1)
Note: Award (M1) for correct substitution into volume formula.
\(2150000\,({{\text{m}}^3})\) (A1)(G2)
which is less than the volume of the pyramid (R1)(ft)
Ahmad is correct. (A1)(ft)
OR
the length of the wall would be \(\frac{{{\text{their part (c)}}}}{{5 \times 1 \times 1000}}\) (M1)
Note: Award (M1) for dividing their part (c) by \(5000.\)
\(516\,({\text{km}})\) (A1)(ft)(G2)
which is more than the distance from Paris to Amsterdam (R1)(ft)
Ahmad is correct. (A1)(ft)
Note: Do not award final (A1) without an explicit comparison. Follow through from part (c) or part (d). Award (R1) for reasoning that is consistent with their working in part (e); comparing two volumes, or comparing two lengths.
Units are required in part (f)(ii).
i) \({\text{A}}{{\text{W}}^2} = {160^2} + {230^2} – 2 \times 160 \times 230 \times \cos \,(15^\circ )\) (M1)(A1)
Note: Award (M1) for substitution into cosine rule formula, (A1) for correct substitution.
\({\text{AW}} = 86.1\,({\text{m}})\,\,\,(86.0689…)\) (A1)(G2)
Note: Award (M0)(A0)(A0) if \({\text{BAW}}\) or \({\text{AWB}}\) is considered to be a right angled triangle.
ii) \({\text{area}} = \frac{1}{2} \times 230 \times 160 \times \sin \,(15^\circ )\) (M1)(A1)
Note: Award (M1) for substitution into area formula, (A1) for correct substitutions.
\( = 4760\,{{\text{m}}^2}\,\,\,(4762.27…\,{{\text{m}}^2})\) (A1)(G2)
Note: The answer is \(4760\,{{\text{m}}^2}\) , the units are required.
Question
A water container is made in the shape of a cylinder with internal height \(h\) cm and internal base radius \(r\) cm.
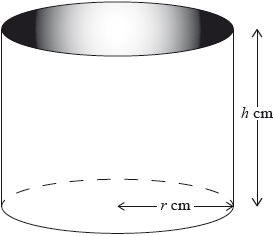
The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.
The volume of the water container is \(0.5{\text{ }}{{\text{m}}^3}\).
The water container is designed so that the area to be coated is minimized.
One can of water-resistant material coats a surface area of \(2000{\text{ c}}{{\text{m}}^2}\).
Write down a formula for \(A\), the surface area to be coated.[2]
Express this volume in \({\text{c}}{{\text{m}}^3}\).[1]
Write down, in terms of \(r\) and \(h\), an equation for the volume of this water container.[1]
Show that \(A = \pi {r^2}\frac{{1\,000\,000}}{r}\).[2]
Show that \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\).[2]
Find \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\).[3]
Using your answer to part (e), find the value of \(r\) which minimizes \(A\).[3]
Find the value of this minimum area.[2]
Find the least number of cans of water-resistant material that will coat the area in part (g).[3]
Answer/Explanation
Markscheme
\((A = ){\text{ }}\pi {r^2} + 2\pi rh\) (A1)(A1)
Note: Award (A1) for either \(\pi {r^2}\) OR \(2\pi rh\) seen. Award (A1) for two correct terms added together.[2 marks]
\(500\,000\) (A1)
Notes: Units not required.[1 mark]
\(500\,000 = \pi {r^2}h\) (A1)(ft)
Notes: Award (A1)(ft) for \(\pi {r^2}h\) equating to their part (b).
Do not accept unless \(V = \pi {r^2}h\) is explicitly defined as their part (b).[1 mark]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).[2 marks]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).[2 marks]
\(2\pi r – \frac{{{\text{1}}\,{\text{000}}\,{\text{000}}}}{{{r^2}}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi r\), (A1) for \(\frac{1}{{{r^2}}}\) or \({r^{ – 2}}\), (A1) for \( – {\text{1}}\,{\text{000}}\,{\text{000}}\).[3 marks]
\(2\pi r – \frac{{1\,000\,000}}{{{r^2}}} = 0\) (M1)
Note: Award (M1) for equating their part (e) to zero.
\({r^3} = \frac{{1\,000\,000}}{{2\pi }}\) OR \(r = \sqrt[3]{{\frac{{1\,000\,000}}{{2\pi }}}}\) (M1)
Note: Award (M1) for isolating \(r\).
OR
sketch of derivative function (M1)
with its zero indicated (M1)
\((r = ){\text{ }}54.2{\text{ }}({\text{cm}}){\text{ }}(54.1926 \ldots )\) (A1)(ft)(G2)[3 marks]
\(\pi {(54.1926 \ldots )^2} + \frac{{1\,000\,000}}{{(54.1926 \ldots )}}\) (M1)
Note: Award (M1) for correct substitution of their part (f) into the given equation.
\( = 27\,700{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}(27\,679.0 \ldots )\) (A1)(ft)(G2)[2 marks]
\(\frac{{27\,679.0 \ldots }}{{2000}}\) (M1)
Note: Award (M1) for dividing their part (g) by 2000.
\( = 13.8395 \ldots \) (A1)(ft)
Notes: Follow through from part (g).
14 (cans) (A1)(ft)(G3)
Notes: Final (A1) awarded for rounding up their \(13.8395 \ldots \) to the next integer.[3 marks]
Question
The following table shows the average body weight, \(x\), and the average weight of the brain, \(y\), of seven species of mammal. Both measured in kilograms (kg).
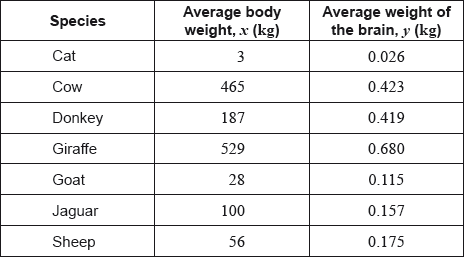
The average body weight of grey wolves is 36 kg.
In fact, the average weight of the brain of grey wolves is 0.120 kg.
The average body weight of mice is 0.023 kg.
Find the range of the average body weights for these seven species of mammal.[2]
For the data from these seven species calculate \(r\), the Pearson’s product–moment correlation coefficient;[2]
For the data from these seven species describe the correlation between the average body weight and the average weight of the brain.[2]
Write down the equation of the regression line \(y\) on \(x\), in the form \(y = mx + c\).[2]
Use your regression line to estimate the average weight of the brain of grey wolves.[2]
Find the percentage error in your estimate in part (d).[2]
State whether it is valid to use the regression line to estimate the average weight of the brain of mice. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
\(529 – 3\) (M1)
\( = 526{\text{ (kg)}}\) (A1)(G2)
[2 marks]
\(0.922{\text{ }}(0.921857 \ldots )\) (G2)[2 marks]
(very) strong, positive (A1)(ft)(A1)(ft)
Note: Follow through from part (b)(i).[2 marks]
\(y = 0.000986x + 0.0923{\text{ }}(y = 0.000985837 \ldots x + 0.0923391…)\) (A1)(A1)
Note: Award (A1) for \(0.000986x\), (A1) for 0.0923.
Award a maximum of (A1)(A0) if the answer is not an equation in the form \(y = mx + c\).[2 marks]
\(0.000985837 \ldots (36) + 0.0923391 \ldots \) (M1)
Note: Award (M1) for substituting 36 into their equation.
\(0.128{\text{ (kg) }}\left( {0.127829 \ldots {\text{ (kg)}}} \right)\) (A1)(ft)(G2)
Note: Follow through from part (c). The final (A1) is awarded only if their answer is positive.[2 marks]
\(\left| {\frac{{0.127829 \ldots – 0.120}}{{0.120}}} \right| \times 100\) (M1)
Note: Award (M1) for their correct substitution into percentage error formula.
\(6.52{\text{ }}(\% ){\text{ }}\left( {6.52442…{\text{ }}(\% )} \right)\) (A1)(ft)(G2)
Note: Follow through from part (d). Do not accept a negative answer.[2 marks]
Not valid (A1)
the mouse is smaller/lighter/weighs less than the cat (lightest mammal) (R1)
OR
as it would mean the mouse’s brain is heavier than the whole mouse (R1)
OR
0.023 kg is outside the given data range. (R1)
OR
Extrapolation (R1)
Note: Do not award (A1)(R0). Do not accept percentage error as a reason for validity.[2 marks]
Question
A pan, in which to cook a pizza, is in the shape of a cylinder. The pan has a diameter of 35 cm and a height of 0.5 cm.
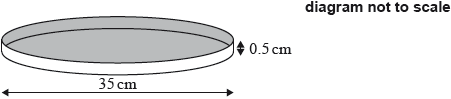
A chef had enough pizza dough to exactly fill the pan. The dough was in the shape of a sphere.
The pizza was cooked in a hot oven. Once taken out of the oven, the pizza was placed in a dining room.
The temperature, \(P\), of the pizza, in degrees Celsius, °C, can be modelled by
\[P(t) = a{(2.06)^{ – t}} + 19,{\text{ }}t \geqslant 0\]
where \(a\) is a constant and \(t\) is the time, in minutes, since the pizza was taken out of the oven.
When the pizza was taken out of the oven its temperature was 230 °C.
The pizza can be eaten once its temperature drops to 45 °C.
Calculate the volume of this pan.[3]
Find the radius of the sphere in cm, correct to one decimal place.[4]
Find the value of \(a\).[2]
Find the temperature that the pizza will be 5 minutes after it is taken out of the oven.[2]
Calculate, to the nearest second, the time since the pizza was taken out of the oven until it can be eaten.[3]
In the context of this model, state what the value of 19 represents.[1]
Answer/Explanation
Markscheme
\((V = ){\text{ }}\pi \times {{\text{(17.5)}}^2} \times 0.5\) (A1)(M1)
Notes: Award (A1) for 17.5 (or equivalent) seen.
Award (M1) for correct substitutions into volume of a cylinder formula.
\( = 481{\text{ c}}{{\text{m}}^3}{\text{ }}(481.056 \ldots {\text{ c}}{{\text{m}}^3},{\text{ }}153.125\pi {\text{ c}}{{\text{m}}^3})\) (A1)(G2)[3 marks]
\(\frac{4}{3} \times \pi \times {r^3} = 481.056 \ldots \) (M1)
Note: Award (M1) for equating their answer to part (a) to the volume of sphere.
\({r^3} = \frac{{3 \times 481.056 \ldots }}{{4\pi }}{\text{ }}( = 114.843 \ldots )\) (M1)
Note: Award (M1) for correctly rearranging so \({r^3}\) is the subject.
\(r = 4.86074 \ldots {\text{ (cm)}}\) (A1)(ft)(G2)
Note: Award (A1) for correct unrounded answer seen. Follow through from part (a).
\( = 4.9{\text{ (cm)}}\) (A1)(ft)(G3)
Note: The final (A1)(ft) is awarded for rounding their unrounded answer to one decimal place.[4 marks]
\(230 = a{(2.06)^0} + 19\) (M1)
Note: Award (M1) for correct substitution.
\(a = 211\) (A1)(G2)[2 marks]
\((P = ){\text{ }}211 \times {(2.06)^{ – 5}} + 19\) (M1)
Note: Award (M1) for correct substitution into the function, \(P(t)\). Follow through from part (c). The negative sign in the exponent is required for correct substitution.
\( = 24.7\) (°C) \((24.6878 \ldots \) (°C)) (A1)(ft)(G2)[2 marks]
\(45 = 211 \times {(2.06)^{ – t}} + 19\) (M1)
Note: Award (M1) for equating 45 to the exponential equation and for correct substitution (follow through for their \(a\) in part (c)).
\((t = ){\text{ }}2.89711 \ldots \) (A1)(ft)(G1)
\(174{\text{ (seconds) }}\left( {173.826 \ldots {\text{ (seconds)}}} \right)\) (A1)(ft)(G2)
Note: Award final (A1)(ft) for converting their \({\text{2.89711}} \ldots \) minutes into seconds.[3 marks]
the temperature of the (dining) room (A1)
OR
the lowest final temperature to which the pizza will cool (A1)[1 mark]
Question
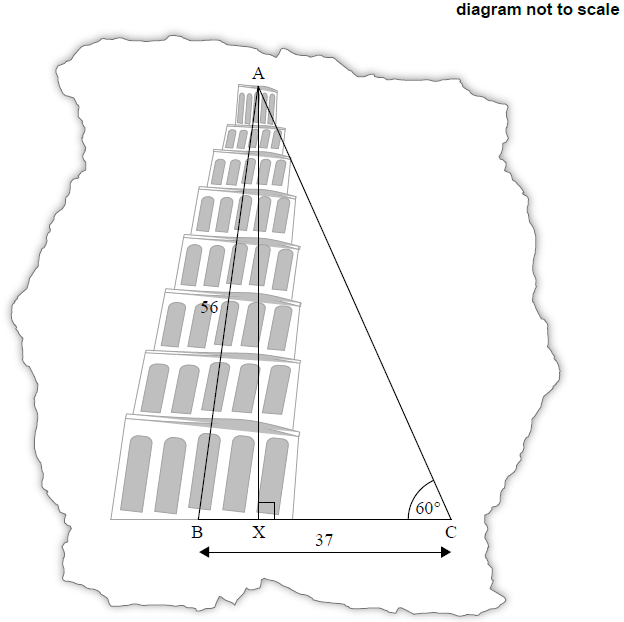
The Tower of Pisa is well known worldwide for how it leans.
Giovanni visits the Tower and wants to investigate how much it is leaning. He draws a diagram showing a non-right triangle, ABC.
On Giovanni’s diagram the length of AB is 56 m, the length of BC is 37 m, and angle ACB is 60°. AX is the perpendicular height from A to BC.
Giovanni’s tourist guidebook says that the actual horizontal displacement of the Tower, BX, is 3.9 metres.
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree.[5]
Use Giovanni’s diagram to calculate the length of AX.[2]
Use Giovanni’s diagram to find the length of BX, the horizontal displacement of the Tower.[2]
Find the percentage error on Giovanni’s diagram.[2]
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.
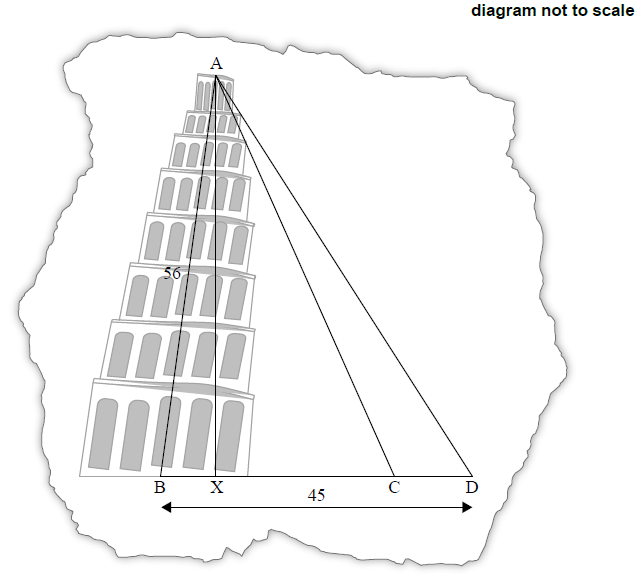
Find the angle of elevation of A from D.[3]
Answer/Explanation
Markscheme
\(\frac{{{\text{sin BAC}}}}{{37}} = \frac{{{\text{sin 60}}}}{{56}}\) (M1)(A1)
Note: Award (M1) for substituting the sine rule formula, (A1) for correct substitution.
angle \({\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{C}}\) = 34.9034…° (A1)
Note: Award (A0) if unrounded answer does not round to 35. Award (G2) if 34.9034… seen without working.
angle \({\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}\) = 180 − (34.9034… + 60) (M1)
Note: Award (M1) for subtracting their angle BAC + 60 from 180.
85.0965…° (A1)
85° (AG)
Note: Both the unrounded and rounded value must be seen for the final (A1) to be awarded. If the candidate rounds 34.9034…° to 35° while substituting to find angle \({\text{A}}\mathop {\text{B}}\limits^ \wedge {\text{C}}\), the final (A1) can be awarded but only if both 34.9034…° and 35° are seen.
If 85 is used as part of the workings, award at most (M1)(A0)(A0)(M0)(A0)(AG). This is the reverse process and not accepted.
sin 85… × 56 (M1)
= 55.8 (55.7869…) (m) (A1)(G2)
Note: Award (M1) for correct substitution in trigonometric ratio.
\(\sqrt {{{56}^2} – 55.7869{ \ldots ^2}} \) (M1)
Note: Award (M1) for correct substitution in the Pythagoras theorem formula. Follow through from part (a)(ii).
OR
cos(85) × 56 (M1)
Note: Award (M1) for correct substitution in trigonometric ratio.
= 4.88 (4.88072…) (m) (A1)(ft)(G2)
Note: Accept 4.73 (4.72863…) (m) from using their 3 s.f answer. Accept equivalent methods.[2 marks]
\(\left| {\frac{{4.88 – 3.9}}{{3.9}}} \right| \times 100\) (M1)
Note: Award (M1) for correct substitution into the percentage error formula.
= 25.1 (25.1282) (%) (A1)(ft)(G2)
Note: Follow through from part (a)(iii).[2 marks]
\({\text{ta}}{{\text{n}}^{ – 1}}\left( {\frac{{55.7869 \ldots }}{{40.11927 \ldots }}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their 40.11927… seen. Award (M1) for correct substitution into trigonometric ratio.
OR
(37 − 4.88072…)2 + 55.7869…2
(AC =) 64.3725…
64.3726…2 + 82 − 2 × 8 × 64.3726… × cos120
(AD =) 68.7226…
\(\frac{{{\text{sin 120}}}}{{68.7226 \ldots }} = \frac{{{\text{sin A}}\mathop {\text{D}}\limits^ \wedge {\text{C}}}}{{64.3725 \ldots }}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their correct values seen, (M1) for correct substitution into the sine formula.
= 54.3° (54.2781…°) (A1)(ft)(G2)
Note: Follow through from part (a). Accept equivalent methods.[3 marks]

