Question
The speed, \(s\) , in \({\text{km }}{{\text{h}}^{ – 1}}\), of \(120\) vehicles passing a point on the road was measured. The results are given below.
Write down the midpoint of the \(60 < s \leqslant 70\) interval.[1]
Use your graphic display calculator to find an estimate for
(i) the mean speed of the vehicles;
(ii) the standard deviation of the speeds of the vehicles.[3]
Write down the number of vehicles whose speed is less than or equal to \({\text{60 km }}{{\text{h}}^{ – 1}}\).[1]
Consider the cumulative frequency table below.
Write down the value of \(a\) , of \(b\) and of \(c\) .[2]
Consider the cumulative frequency table below.
Draw a cumulative frequency graph for the information from the table. Use \(1\) cm to represent \({\text{10 km }}{{\text{h}}^{ – 1}}\) on the horizontal axis and \(1\) cm to represent \(10\) vehicles on the vertical axis.[4]
Use your cumulative frequency graph to estimate
(i) the median speed of the vehicles;
(ii) the number of vehicles that are travelling at a speed less than or equal to \({\text{65 km }}{{\text{h}}^{ – 1}}\).[4]
All drivers whose vehicle’s speed is greater than one standard deviation above the speed limit of \({\text{50 km }}{{\text{h}}^{ – 1}}\) will be fined.
Use your graph to estimate the number of drivers who will be fined.[3]
Answer/Explanation
Markscheme
\(65\) (A1)[1 mark]
(i) \(54{\text{ (km }}{{\text{h}}^{ – 1}})\) (G2)
Note: If the answer to part (b)(i) is consistent with the answer to part (a) then award (G2)(ft) even if no working seen.
(ii) \(19.2\) (\(19.2093 \ldots \)) (G1)
Note: Accept \(19\), do not accept \(20\).[3 marks]
\(76\) (A1)[1 mark]
\(a = 76\), \(b = 98\) (A1)(ft)
Note: Follow through from their answer to part (c) for \(a\) and \(b = \) their \(a + 22\) .
\(c = 118\) (A1)[2 marks]
(A1)(A1)(ft)(A1)(ft)(A1)
Notes: Award (A1) for axes labelled and correct scales. If the axes are reversed do not award this mark but follow through. Award (A2)(ft) for their 6 points correct, (A1)(ft) for at least 3 of these points correct. Award (A1) for smooth curve drawn through all points including (\(0\), \(0\)). If either the \(x\) or the \(y\) axis has a break in it to zero, do not award this final mark.[4 marks]
(i) \(57\) \({\text{(km }}{{\text{h}}^{ – 1}})\) \(( \pm 2)\) (M1)(A1)(ft)(G2)
Note: Award (M1) for clear indication of median on their graph. Follow through from their graph. If their answer is consistent with their incorrect graph but there is no working present on graph then no marks are awarded.
(ii) \(90\) vehicles \(( \pm 2)\) (M1)(A1)(ft)(G2)
Note: Award (M1) for clear indication of method on their graph. Follow through from their graph. If their answer is consistent with their incorrect graph but there is no working present on graph then no marks are awarded.[4 marks]
\(50 + 19.2 = 69.2\) (A1)(ft)
\(24\) \(( \pm 2)\) drivers will be fined (M1)(A1)(ft)(G2)
Notes: Follow through from their graph and from their part (b)(ii). Award (M1) for indication of method on their graph. If their answer is consistent with their incorrect graph but there is no working present on graph then no marks are awarded.[3 marks]
Question
200 people were asked the amount of time T (minutes) they had spent in the supermarket. The results are represented in the table below.
State if the data is discrete or continuous.[1]
State the modal group.[1]
Write down the midpoint of the interval 10 < T ≤ 20 .[1]
Use your graphic display calculator to find an estimate for
(i) the mean;
(ii) the standard deviation.[3]
The results are represented in the cumulative frequency table below, with upper class boundaries of 10, 20, 30, 40, 50.
Write down the value of
(i) q;
(ii) r.[2]
The results are represented in the cumulative frequency table below, with upper class boundaries of 10, 20, 30, 40, 50.
On graph paper, draw a cumulative frequency graph, using a scale of 2 cm to represent 10 minutes (T) on the horizontal axis and 1 cm to represent 10 people on the vertical axis.[4]
Use your graph from part (f) to estimate
(i) the median;
(ii) the 90th percentile of the results;
(iii) the number of people who shopped at the supermarket for more than 15 minutes.[6]
Answer/Explanation
Markscheme
continuous (A1)[1 mark]
20 < T ≤ 30 (A1)[1 mark]
15 (A1)[1 mark]
(i) 21.5 (G2)
(ii) 9.21 (9.20597…) (G1)[3 marks]
(i) q = 194 (A1)
(ii) r = 200 (A1)[2 marks]
(A1)(A2)(ft)(A1)
Notes: Award (A1) for scale and axis labels, (A2)(ft) for 5 correct points, (A1)(ft) for 4 or 3 correct points, (A0) for less than 3 correct points, (A1) for smooth curve through their points, starting at (0, 0). Follow through from their answers to parts (e)(i) and (e)(ii).[4 marks]
(i) 22.5 ± 2 (A1)
(ii) 32 ± 2 (M1)(A1)(ft)(G2)
Note: Award (M1) for lines drawn on graph or some indication of method, follow through from their graph if working is shown.(iii) 44 ± 2 (A1)(ft)
Note: Follow through from their graph if working is shown.
200 − 44 = 156 (M1)(A1)(ft)(G2)
Note: Award (M1) for subtraction from 200, follow through from their graph if working is shown.[6 marks]
Question
A survey was conducted to determine the length of time, \(t\), in minutes, people took to drink their coffee in a café. The information is shown in the following grouped frequency table.
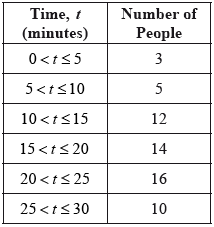
Write down the total number of people who were surveyed.[1]
Write down the mid-interval value for the \(10 < t \leqslant 15\) group.[1]
Find an estimate of the mean time people took to drink their coffee.[2]
The information above has been rewritten as a cumulative frequency table.

Write down the value of \(a\) and the value of \(b\).[2]
This information is shown in the following cumulative frequency graph.
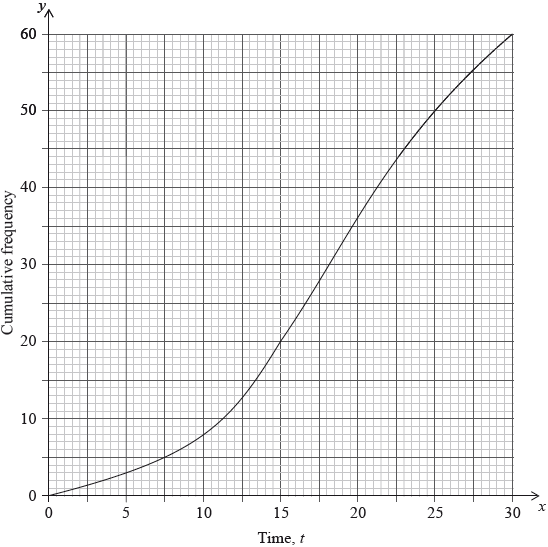
For the people who were surveyed, use the graph to estimate
(i) the time taken for the first \(40\) people to drink their coffee;
(ii) the number of people who take less than \(8\) minutes to drink their coffee;
(iii) the number of people who take more than \(23\) minutes to drink their coffee.[4]
Answer/Explanation
Markscheme
\(60\) (A1)[1 mark]
\(12.5\) (A1)[1 mark]
\(\frac{{3 \times 2.5 + 5 \times 7.5 + \ldots + 10 \times 27.5}}{{60}}\) (M1)
Note: Award (M1) for an attempt to substitute their mid-interval values (consistent with their answer to part (b)) into the formula for the mean.
Award (M1) where a table is constructed with their (consistent) mid-interval values listed along with the frequencies.
\( = \frac{{1075}}{{60}}{\text{ }}\left( {\frac{{215}}{{12}},{\text{ 17.9, 17.9166}} \ldots } \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (b).[2 marks]
\(a = 34,{\text{ }}b = 60\) (A1)(A1)[2 marks]
(i) \( \leqslant {\text{21.25 minutes}}\) (A1)
Note: Accept \(21.25\).
Accept any answer between \(21\) and \(21.5\).
(Accept 21.5, but do not accept 21.)
(ii) \(5\) (A1)
Note: Accept \( < 6\). Do not accept \(6\).
Answer must be an integer.
(iii) \(60 – 45\) (M1)
\( = 15\) (A1)(G2)
Notes: Award (M1) for subtraction from \(60\). Accept \(15 \pm 1\).
Answer must be an integer.[4 marks]
Question
The cumulative frequency graph shows the speed, \(s\), in \({\text{km}}\,{{\text{h}}^{ – 1}}\), of \(120\) vehicles passing a hospital gate.
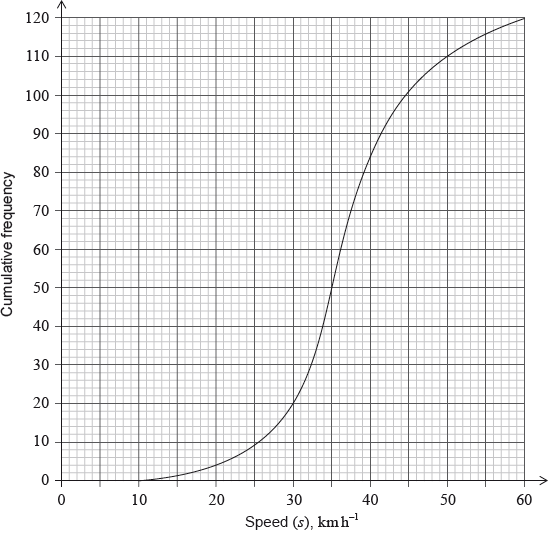
Estimate the minimum possible speed of one of these vehicles passing the hospital gate.[1]
Find the median speed of the vehicles.[2]
Write down the \({75^{{\text{th}}}}\) percentile.[1]
Calculate the interquartile range.[2]
The speed limit past the hospital gate is \(50{\text{ km}}\,{{\text{h}}^{ – 1}}\).
Find the number of these vehicles that exceed the speed limit.[2]
The table shows the speeds of these vehicles travelling past the hospital gate.
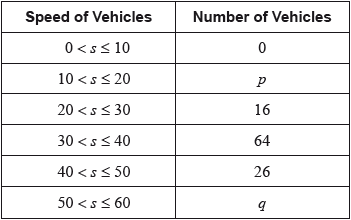
Find the value of \(p\) and of \(q\).[2]
The table shows the speeds of these vehicles travelling past the hospital gate.

(i) Write down the modal class.
(ii) Write down the mid-interval value for this class.[2]
The table shows the speeds of these vehicles travelling past the hospital gate.

Use your graphic display calculator to calculate an estimate of
(i) the mean speed of these vehicles;
(ii) the standard deviation.[3]
It is proposed that the speed limit past the hospital gate is reduced to \(40{\text{ km}}\,{{\text{h}}^{ – 1}}\) from the current \(50{\text{ km}}\,{{\text{h}}^{ – 1}}\).
Find the percentage of these vehicles passing the hospital gate that do not exceed the current speed limit but would exceed the new speed limit.[2]
Answer/Explanation
Markscheme
\(10{\text{ (km}}\,{{\text{h}}^{ – 1}})\) (A1)
\(36\) (G2)
\(41.5\) (G1)
\(41.5 – 32.5\) (M1)
\( = 9{\text{ (}} \pm {\text{1)}}\) (A1)(ft)(G2)
Notes: Award (M1) for quartiles seen. Follow through from part (c).
\(120 – 110\) (M1)
\( = 10\) (A1)(G2)
Note: Award (M1) for \(110\) seen.
\(p = 4\;\;\;q = 10\) (A1)(ft)(A1)(ft)
Note: Follow through from part (e).
(i) \(30 < s \leqslant 40\) (A1)
(ii) \(35\) (A1)(ft)
Note: Follow through from part (g)(i).
(i) \(36.8{\text{ (km}}\,{{\text{h}}^{ – 1}})\;\;\;(36.8333)\) (G2)(ft)
Notes: Follow through from part (f).
(ii) \(8.85\;\;\;(8.84904 \ldots )\) (G1)(ft)
Note: Follow through from part (f), irrespective of working seen.
\(\frac{{26}}{{120}} \times 100\) (M1)
Note: Award (M1) for \(\frac{{26}}{{120}} \times 100\) seen.
\( = 21.7{\text{ (}}\% )\;\;\;\left( {21.6666 \ldots ,{\text{ }}21\frac{2}{3},{\text{ }}\frac{{65}}{3}} \right)\) (A1)(G2)
Question
A transportation company owns 30 buses. The distance that each bus has travelled since being purchased by the company is recorded. The cumulative frequency curve for these data is shown.
It is known that 8 buses travelled more than m kilometres.
Find the number of buses that travelled a distance between 15000 and 20000 kilometres.[2]
Use the cumulative frequency curve to find the median distance.[2]
Use the cumulative frequency curve to find the lower quartile.[1]
Use the cumulative frequency curve to find the upper quartile.[1]
Hence write down the interquartile range.[1]
Write down the percentage of buses that travelled a distance greater than the upper quartile.[1]
Find the number of buses that travelled a distance less than or equal to 12 000 km.[1]
Find the value of m.[2]
The smallest distance travelled by one of the buses was 2500 km.
The longest distance travelled by one of the buses was 23 000 km.
On graph paper, draw a box-and-whisker diagram for these data. Use a scale of 2 cm to represent 5000 km.[4]
Answer/Explanation
Markscheme
28 − 20 (A1)
Note: Award (A1) for 28 and 20 seen.
8 (A1)(G2)[2 marks]
13500 (G2)
Note: Accept an answer in the range 13500 to 13750.[2 marks]
10000 (G1)
Note: Accept an answer in the range 10000 to 10250.[1 mark]
16000 (G1)
Note: Accept an answer in the range 16000 to 16250.[1 mark]
6000 (A1)(ft)
Note: Follow through from their part (b)(ii) and (iii).[1 mark]
25% (A1)[1 mark]
11 (G1)[1 mark]
30 − 8 OR 22 (M1)
Note: Award (M1) for subtracting 30 − 8 or 22 seen.
15750 (A1)(G2)
Note: Accept 15750 ± 250.[2 marks]
(A1)(A1)(A1)(A1)
Note: Award (A1) for correct label and scale; accept “distance” or “km” for label.
(A1)(ft) for correct median,
(A1)(ft) for correct quartiles and box,
(A1) for endpoints at 2500 and 23 000 joined to box by straight lines.
Accept ±250 for the median, quartiles and endpoints.
Follow through from their part (b).
The final (A1) is not awarded if the line goes through the box.[4 marks]

