Download IITian Academy App for accessing Online Mock Tests and More..
Question
A geometric sequence has second term 12 and fifth term 324.
Consider the following propositions
p: The number is a multiple of five.
q: The number is even.
r: The number ends in zero.
Calculate the value of the common ratio.[4]
Calculate the 10th term of this sequence.[3]
The kth term is the first term which is greater than 2000. Find the value of k.[3]
Write in words \((q \wedge \neg r) \Rightarrow \neg p\).[3]
Consider the statement “If the number is a multiple of five, and is not even then it will not end in zero”.
Write this statement in symbolic form.[4]
Consider the statement “If the number is a multiple of five, and is not even then it will not end in zero”.
Write the contrapositive of this statement in symbolic form.[2]
Answer/Explanation
Markscheme
u1r4 = 324 (A1)
u1r = 12 (A1)
r3 = 27 (M1)
r = 3 (A1)(G3)
Note: Award at most (G3) for trial and error.[4 marks]
4 × 39 = 78732 or 12 × 38 = 78732 (A1)(M1)(A1)(ft)(G3)
Note: Award (A1) for u1 = 4 if n = 9 , or u1 = 12 if n = 8, (M1) for correctly substituted formula.
(ft) from their (a).[3 marks]
4 × 3k−1 > 2000 (M1)
Note: Award (M1) for correct substitution in correct formula. Accept an equation.
k > 6 (A1)
k = 7 (A1)(ft)(G2)
Notes: If second line not seen award (A2) for correct answer. (ft) from their (a).
Accept a list, must see at least 3 terms including the 6th and 7th.
Note: If arithmetic sequence formula is used consistently in parts (a), (b) and (c), award (A0)(A0)(M0)(A0) for (a) and (ft) for parts (b) and (c).[3 marks]
If the number is even and the number does not end in zero, (then) the number is not a multiple of five. (A1)(A1)(A1)
Note: Award (A1) for “if…(then)”, (A1) for “the number is even and the number does not end in zero”, (A1) for the number is not a multiple of 5.[3 marks]
\((p \wedge \neg q) \Rightarrow \neg r\) (A1)(A1)(A1)(A1)
(A1) for \(\Rightarrow\), (A1) for \(\wedge\), (A1) for p and \(\neg q\), (A1) for \(\neg r\)
Note: If parentheses not present award at most (A1)(A1)(A1)(A0).[4 marks]
\(r \Rightarrow (\neg p \vee q)\) OR \(r \Rightarrow \neg (p \wedge \neg q)\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for reversing the order, (A1) for negating the statements on both sides.
If parentheses not present award at most (A1)(ft)(A0).
Do not penalise twice for missing parentheses in (i) and (ii).[2 marks]
Question
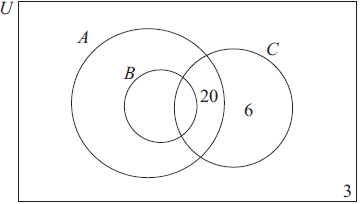
The Venn diagram below represents the students studying Mathematics (A), Further Mathematics (B) and Physics (C) in a school.
50 students study Mathematics
38 study Physics
20 study Mathematics and Physics but not Further Mathematics
10 study Further Mathematics but not Physics
12 study Further Mathematics and Physics
6 study Physics but not Mathematics
3 study none of these three subjects.
Three propositions are given as
p : It is snowing q : The roads are open r : We will go skiing
Copy and complete the Venn diagram on your answer paper.[3]
Write down the number of students who study Mathematics but not Further Mathematics.[1]
Write down the total number of students in the school.[1]
Write down \(n({\text{B}} \cup {\text{C}})\).[2]
Write the following compound statement in symbolic form.
“It is snowing and the roads are not open.”[2]
Write the following compound statement in words.
\((\neg p \wedge q) \Rightarrow r\)[3]
An incomplete truth table for the compound proposition \((\neg p \wedge q) \Rightarrow r\) is given below.
Copy and complete the truth table on your answer paper.
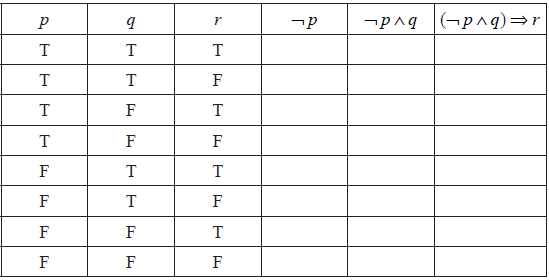[3]
Answer/Explanation
Markscheme
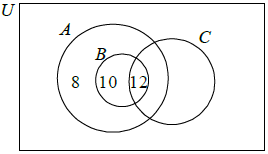(A1)(A1)(A1)
Note: Award (A1) for each correct number in the correct position.[3 marks]
28 (A1)(ft)
Note: 20 + their 8.[1 mark]
59 (A1)(ft)[1 mark]
10 + 12 + 20 + 6 (M1)
Note: Award (M1) for use of the correct regions.
= 48 (A1)(ft)(G2)
OR
59 − 8 − 3 (M1)
= 48 (A1)(ft)[2 marks]
\(p \wedge \neg q\) (A1)(A1)
Note: Award (A1) for \(\wedge\), (A1) for both statements in the correct order.[2 marks]
If it is not snowing and the roads are open (then) we will go skiing. (A1)(A1)(A1)
Note: Award (A1) for “if…(then)”, (A1) for “not snowing and the roads are open”, (A1) for “we will go skiing”.[3 marks]
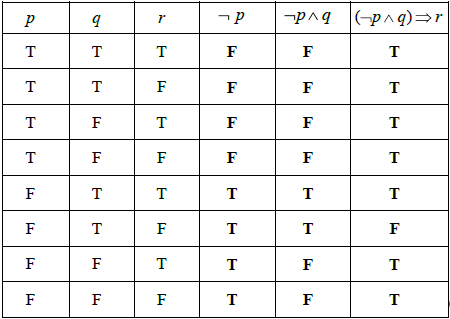(A1)(A1)(ft)(A1)(ft)
Note: Award (A1) for each correct column.[3 marks]
Question
Consider the following statements.
\(p\): the land has been purchased
\(q\): the building permit has been obtained
\(r\): the land can be used for residential purposes
Write the following argument in symbolic form.
“If the land has been purchased and the building permit has been obtained, then the land can be used for residential purposes.”[3]
In your answer booklet, copy and complete a truth table for the argument in part (a).
Begin your truth table as follows.
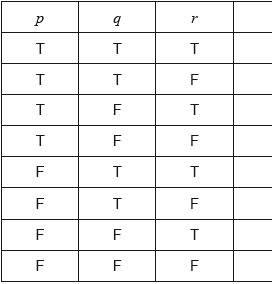[2]
Use your truth table to determine whether the argument in part (a) is valid.
Give a reason for your decision.[2]
Write down the inverse of the argument in part (a)
(i) in symbolic form;
(ii) in words.[4]
Answer/Explanation
Markscheme
\((p \wedge q) \Rightarrow r\) (A1)(A1)(A1)
Notes: Award (A1) for conjunction seen, award (A1) for implication seen, award (A1) for correct simple propositions in correct order (the parentheses are required). Accept \(r \Leftarrow (p \wedge q)\).
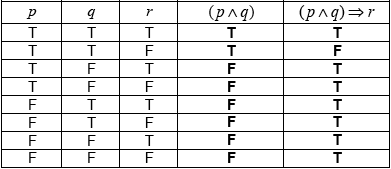(A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for each correct column, follow through to the final column from their \((p \wedge q)\) column. For the second (A1)(ft) to be awarded there must be an implication in part (a).
Follow through from part (a).
The argument is not valid since not all entries in the final column are T. (A1)(ft)(R1)
Notes: Do not award (A1)(ft)(R0). Follow through from part (b).
Accept “The argument is not valid since \((p \wedge q) \Rightarrow r\) is not a tautology”.
(i) \(\neg (p \wedge q) \Rightarrow \neg r\) (A1)(ft)(A1)(ft)
OR
\((\neg p \vee \neg q) \Rightarrow \neg r\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for the negation of their antecedent and the negation of their consequent, (A1)(ft) for their fully correct answer.
Follow through from part (a). Accept \(\neg r \Leftarrow \neg (p \wedge q)\) or \(\neg r \Leftarrow (\neg p \vee \neg q)\). Follow through from part (a).
(ii) if it is not the case that the land has been purchased and the building permit has been obtained then the land can not be used for residential purposes. (A1)(A1)(ft)
OR
if (either) the land has not been purchased or the building permit has not been obtained then the land can not be used for residential purposes. (A1)(A1)(ft)
Notes: Award (A1) for “if… then…” seen, (A1)(ft) for correct statements in correct order. Follow through from part (d)(i).
Question
A water container is made in the shape of a cylinder with internal height \(h\) cm and internal base radius \(r\) cm.
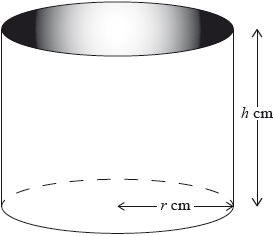
The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.
The volume of the water container is \(0.5{\text{ }}{{\text{m}}^3}\).
The water container is designed so that the area to be coated is minimized.
One can of water-resistant material coats a surface area of \(2000{\text{ c}}{{\text{m}}^2}\).
Write down a formula for \(A\), the surface area to be coated.[2]
Express this volume in \({\text{c}}{{\text{m}}^3}\).[1]
Write down, in terms of \(r\) and \(h\), an equation for the volume of this water container.[1]
Show that \(A = \pi {r^2}\frac{{1\,000\,000}}{r}\).[2]
Show that \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\).[2]
Find \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\).[3]
Using your answer to part (e), find the value of \(r\) which minimizes \(A\).[3]
Find the value of this minimum area.[2]
Find the least number of cans of water-resistant material that will coat the area in part (g).[3]
Answer/Explanation
Markscheme
\((A = ){\text{ }}\pi {r^2} + 2\pi rh\) (A1)(A1)
Note: Award (A1) for either \(\pi {r^2}\) OR \(2\pi rh\) seen. Award (A1) for two correct terms added together.[2 marks]
\(500\,000\) (A1)
Notes: Units not required.[1 mark]
\(500\,000 = \pi {r^2}h\) (A1)(ft)
Notes: Award (A1)(ft) for \(\pi {r^2}h\) equating to their part (b).
Do not accept unless \(V = \pi {r^2}h\) is explicitly defined as their part (b).[1 mark]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).[2 marks]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).[2 marks]
\(2\pi r – \frac{{{\text{1}}\,{\text{000}}\,{\text{000}}}}{{{r^2}}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi r\), (A1) for \(\frac{1}{{{r^2}}}\) or \({r^{ – 2}}\), (A1) for \( – {\text{1}}\,{\text{000}}\,{\text{000}}\).[3 marks]
\(2\pi r – \frac{{1\,000\,000}}{{{r^2}}} = 0\) (M1)
Note: Award (M1) for equating their part (e) to zero.
\({r^3} = \frac{{1\,000\,000}}{{2\pi }}\) OR \(r = \sqrt[3]{{\frac{{1\,000\,000}}{{2\pi }}}}\) (M1)
Note: Award (M1) for isolating \(r\).
OR
sketch of derivative function (M1)
with its zero indicated (M1)
\((r = ){\text{ }}54.2{\text{ }}({\text{cm}}){\text{ }}(54.1926 \ldots )\) (A1)(ft)(G2)[3 marks]
\(\pi {(54.1926 \ldots )^2} + \frac{{1\,000\,000}}{{(54.1926 \ldots )}}\) (M1)
Note: Award (M1) for correct substitution of their part (f) into the given equation.
\( = 27\,700{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}(27\,679.0 \ldots )\) (A1)(ft)(G2)[2 marks]
\(\frac{{27\,679.0 \ldots }}{{2000}}\) (M1)
Note: Award (M1) for dividing their part (g) by 2000.
\( = 13.8395 \ldots \) (A1)(ft)
Notes: Follow through from part (g).
14 (cans) (A1)(ft)(G3)
Notes: Final (A1) awarded for rounding up their \(13.8395 \ldots \) to the next integer.[3 marks]