Download IITian Academy App for accessing Online Mock Tests and More..
Question
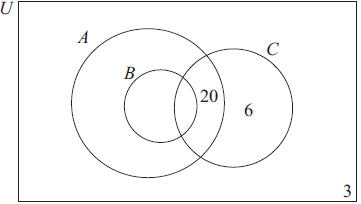
The Venn diagram below represents the students studying Mathematics (A), Further Mathematics (B) and Physics (C) in a school.
50 students study Mathematics
38 study Physics
20 study Mathematics and Physics but not Further Mathematics
10 study Further Mathematics but not Physics
12 study Further Mathematics and Physics
6 study Physics but not Mathematics
3 study none of these three subjects.
Three propositions are given as
p : It is snowing q : The roads are open r : We will go skiing
Copy and complete the Venn diagram on your answer paper.[3]
Write down the number of students who study Mathematics but not Further Mathematics.[1]
Write down the total number of students in the school.[1]
Write down \(n({\text{B}} \cup {\text{C}})\).[2]
Write the following compound statement in symbolic form.
“It is snowing and the roads are not open.”[2]
Write the following compound statement in words.
\((\neg p \wedge q) \Rightarrow r\)[3]
An incomplete truth table for the compound proposition \((\neg p \wedge q) \Rightarrow r\) is given below.
Copy and complete the truth table on your answer paper.
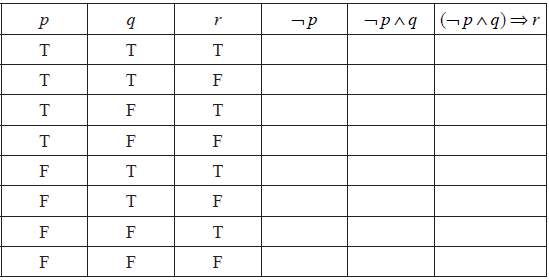[3]
Answer/Explanation
Markscheme
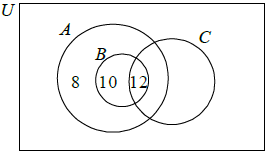(A1)(A1)(A1)
Note: Award (A1) for each correct number in the correct position.[3 marks]
28 (A1)(ft)
Note: 20 + their 8.[1 mark]
59 (A1)(ft)[1 mark]
10 + 12 + 20 + 6 (M1)
Note: Award (M1) for use of the correct regions.
= 48 (A1)(ft)(G2)
OR
59 − 8 − 3 (M1)
= 48 (A1)(ft)[2 marks]
\(p \wedge \neg q\) (A1)(A1)
Note: Award (A1) for \(\wedge\), (A1) for both statements in the correct order.[2 marks]
If it is not snowing and the roads are open (then) we will go skiing. (A1)(A1)(A1)
Note: Award (A1) for “if…(then)”, (A1) for “not snowing and the roads are open”, (A1) for “we will go skiing”.[3 marks]
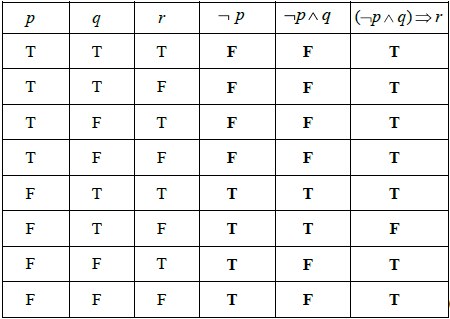(A1)(A1)(ft)(A1)(ft)
Note: Award (A1) for each correct column.[3 marks]
Question
Consider these three propositions, in which x is a natural number.
\[\begin{array}{*{20}{l}} {p{\text{: }}x{\text{ is a factor of 60}}} \\ {q{\text{: }}x{\text{ is a multiple of 4}}} \\ {r{\text{: }}x{\text{ is a multiple of 5}}} \end{array}\]
Write down in symbolic form the compound proposition
“If \(x\) is a factor of 60 then \(x\) is a multiple of 5 or \(x\) is not a multiple of 4.”[3]
Write down in words the compound proposition \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\).[3]
Copy the following truth table and complete the last three columns.
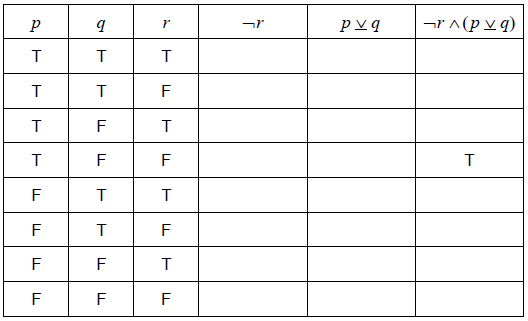[3]
State why the compound proposition \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\) is not a logical contradiction.[1]
A row from the truth table from part (c) is given below.
Write down one value of \(x\) that satisfies these truth values.[1]
Answer/Explanation
Markscheme
\(p \Rightarrow (r \vee \neg q)\) (A1)(A1)(A1)
Note: Award (A1) for “\(p \Rightarrow \)”.
Award (A1) for “\(r \vee \neg q\)” or “\(r \vee q\)” (or “\(\neg q \vee r\)”or “\(q \vee r\)”)
Award (A1) for “\(\neg q\)”.
Award at most (A1)(A1)(A0) if parentheses are missing for \(r \vee \neg q\).
Award (A0)(A0)(A1) for \((p \Rightarrow r) \vee \neg q\).[3 marks]
\(x\) is not a multiple of 5 and (\(x\)) is (either) a factor of 60 or (\(x\)) is a multiple of 4, but not both (A1)(A1)(A1)
Note: Award (A1) for “\(x\) is not a multiple of 5”, (A1) for “(\(x\)) is a factor of 60 or (\(x\)) is a multiple of 4 but not both”, (A1) for “and” in the correct position. Accept only “but not both” in the second (A1).
Award at most (A1)(A1)(A0) for using extra statements such as “If …then”, “if and only if” etc.[3 marks]
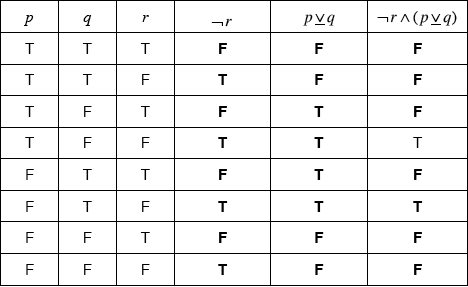(A1)(A1)(A1)(ft)
Note: Award (A1) for each correct column. Last column follows through from previous two.[3 marks]
because not all the entries in the \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\) column are F (R1)(ft)
Note: If all entries in the last column of their truth table are T, award (R1)(ft) for an answer of “it is a tautology”. Only award (R1)(ft) if the column is identified in the justification.[1 mark]
accept one of: 1\(\,\,\,\)OR\(\,\,\,\)2\(\,\,\,\)OR\(\,\,\,\)3\(\,\,\,\)OR\(\,\,\,\)6 (A1)
Note: Award (A1) for any one of the above answers.[1 mark]