Download IITian Academy App for accessing Online Mock Tests and More..
Question
A school offers three activities, basketball (B), choir (C) and drama (D). Every student must participate in at least one activity.
16 students play basketball only.
18 students play basketball and sing in the choir but do not do drama.
34 students play basketball and do drama but do not sing in the choir.
27 students are in the choir and do drama but do not play basketball.
Enter the above information on the Venn diagram below.
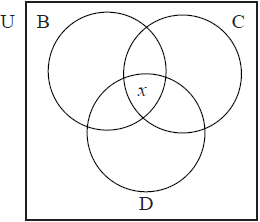[2]
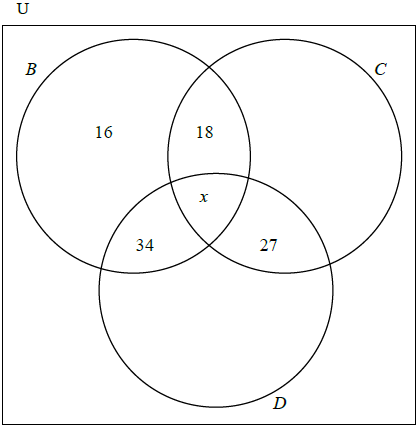
99 of the students play basketball, 88 sing in the choir and 110 do drama.
Calculate the number of students x participating in all three activities.[1]
99 of the students play basketball, 88 sing in the choir and 110 do drama.
Calculate the total number of students in the school.[3]
Answer/Explanation
Markscheme
(A2)
(A1) only if 1 error
(A0) otherwise (C2)[2 marks]
\(x + 16 + 18 + 34 = 99\)
\(x = 31\) (A1) (C1)[1 mark]
Choir only \(= 88 – (18 + 27 + 31) = 12\) (A1)(ft)
Drama only \( = 110 – (27 + 34 + 31) = 18\) (A1)(ft)
Total \( = 16 + 34 + 18 + 31 + 12 + 27 + 18 = 156\) (A1)(ft) (C3)[3 marks]
Question
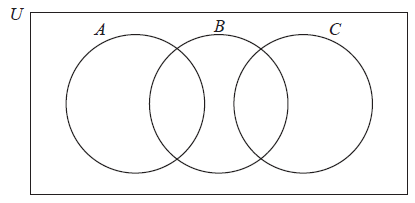
Shade \((A \cup B) \cap C’\) on the diagram below.
[2]
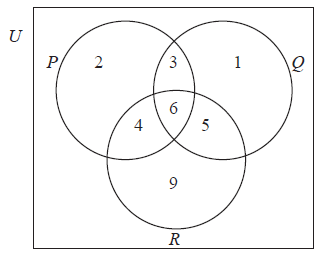
In the Venn diagram below, the number of elements in each region is given.
Find \(n((P \cap Q) \cup R)\).
[2]
\(U\) is the set of positive integers, \({\mathbb{Z}^ + }\).
\(E\) is the set of even numbers.
\(M\) is the set of multiples of \(3\).
(i) List the first six elements of the set \(M\).
(ii) List the first six elements of the set \(E’ \cap M\).[2]
Answer/Explanation
Markscheme
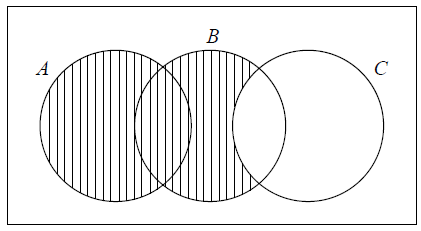
not shading \(C\) or shading \(A \cup B\) (A1)
correct shading (A1) (C2)[2 marks]
Identifying the correct 5 numbers \(3\), \(4\), \(5\), \(6\), \(9\) (A1)
\(27\) (A1) (C2)[2 marks]
(i) \(M = \{ 3{\text{, }}6{\text{, }}9{\text{, }}12{\text{, }}15{\text{, }}18\} \) brackets not required. (A1)
(ii) \(E’ \cap M = \{ 3{\text{, }}9{\text{, }}15{\text{, }}21{\text{, }}27{\text{, }}33\} \) (ft) from (i). (A1)(ft) (C2)[2 marks]
Question
The Venn diagram shows the numbers of pupils in a school according to whether they study the sciences Physics (\(P\)), Chemistry (\(C\)), Biology (\(B\)).
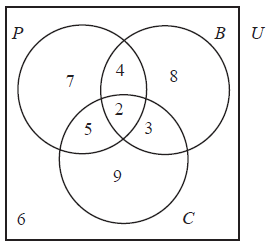
Write down the number of pupils that study Chemistry only.[1]
Write down the number of pupils that study exactly two sciences.[1]
Write down the number of pupils that do not study Physics.[2]
Find \(n[(P \cup B) \cap C]\) .[2]
Answer/Explanation
Markscheme
\(9\) (A1) (C1)[1 mark]
\(12\) (A1) (C1)[1 mark]
\(8 + 3 + 9 + 6\) (M1)
\( = 26\) (A1) (C2)
Note: Award (A1) for \(20\) seen if answer is incorrect.[2 marks]
\(5 + 2 + 3\) (M1)
\( = 10\) (A1) (C2)
Note: Award (A1) for \(29\) or \(19\) seen if answer is incorrect.[2 marks]
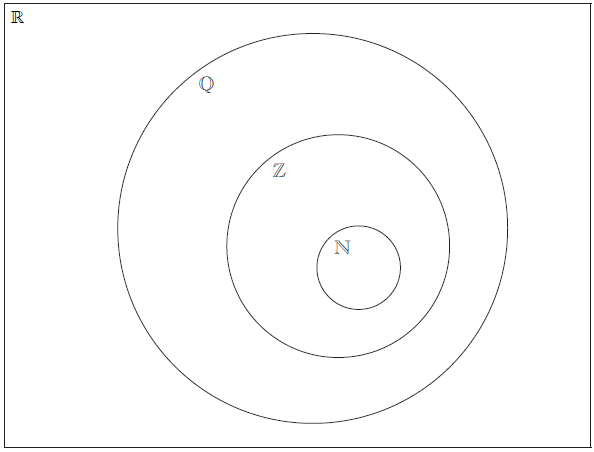
Question
The Venn diagram shows the number sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\). Place each of the following numbers in the appropriate region of the Venn diagram.
\(\frac{{1}}{{4}}\), −3, π, cos 120°, 2.7 × 103, 3.4 × 10–2
Answer/Explanation
Markscheme
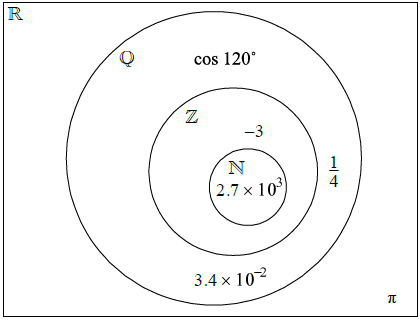(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number placed once in the correct section. Accept equivalent forms for numbers.[6 marks]
Question
A class consists of students studying Spanish or French or both. Fifteen students study Spanish and twelve study French.
The probability that a student studies French given that she studies Spanish is \(\frac{{7}}{{15}}\).
Draw a Venn diagram in the space below to illustrate this information.[3]
Find the probability that a student studies Spanish given that she studies one language only.[3]
Answer/Explanation
Markscheme
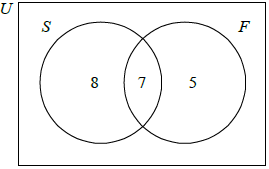(A1)(A1)(A1) (C3)
Note: Award (A1) for a labeled Venn diagram with appropriate sets.
(A1) for 7, (A1) for 8 and 5.[3 marks]
\({\text{P (Spanish / one language only)}} = \frac{{\frac{8}{{20}}}}{{\frac{8}{{20}} + \frac{5}{{20}}}}\) (M1)(A1)(ft)
Note: Award (M1) for substituted conditional probability formula, (A1) for correct substitution. Follow through from their Venn diagram.
\( = \frac{8}{{13}}(0.615,{\text{ }}61.5\% )\) (A1)(ft)
OR
\({\text{P}}{\text{ (Spanish / one language only)}} = \frac{8}{{8 + 5}}\) (A1)(ft)(M1)
Note: Award (A1) for their correct numerator, (M1) for correct recognition of regions. Follow through from their Venn diagram.
\( = \frac{8}{{13}}(0.615,{\text{ }}61.5\% )\) (A1)(ft) (C3)[3 marks]
Question
The sets \(P\), \(Q\) and \(U\) are defined as
U = {Real Numbers} , P = {Positive Numbers} and Q = {Rational Numbers}.
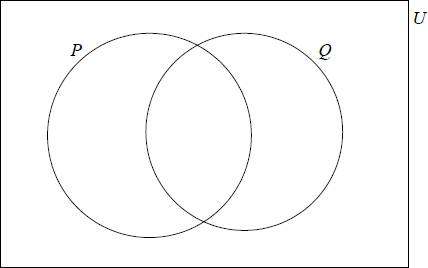
Write down in the correct region on the Venn diagram the numbers
\(\frac{{22}}{7}\) , \(5 \times {10^{ – 2}}\) , \(\sin (60^\circ )\) , \(0\) , \(\sqrt[3]{{ – 8}}\) , \( – \pi \).
Answer/Explanation
Markscheme
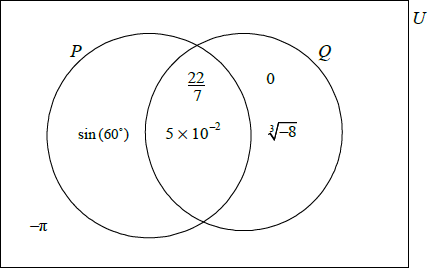(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number placed once in the correct region. Accept equivalent forms for numbers.[6 marks]
Question
A fitness club has 60 members. 35 of the members attend the club’s aerobics course (A) and 28 members attend the club’s yoga course (Y). 17 members attend both courses. A Venn diagram is used to illustrate this situation.
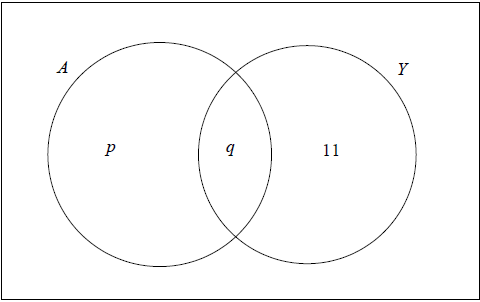
Write down the value of q.[1]
Find the value of p.[2]
Calculate the number of members of the fitness club who attend neither the aerobics course (A) nor the yoga course (Y).[2]
Shade, on your Venn diagram, \(A’ \cap Y\) .[1]
Answer/Explanation
Markscheme
17 (A1) (C1)[1 mark]
35 – 17 (M1)
= 18 (A1) (C2)
Note: Award (A1) for correct answer only.[2 marks]
\(60 – (35 – 17) – (28 – 17) – 17\) (M1)
= 14 (A1)(ft) (C2)
Note: Follow through from (a) and (b).[2 marks]
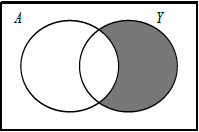(A1) (C1)[1 mark]
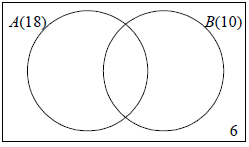
Question
A group of 30 students were asked about their favourite topping for toast.
18 liked peanut butter (A)
10 liked jam (B)
6 liked neither
Show this information on the Venn diagram below.
[2]
Find the number of students who like both peanut butter and jam.[2]
Find the probability that a randomly chosen student from the group likes peanut butter, given that they like jam.[2]
Answer/Explanation
Markscheme
OR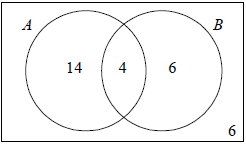 
(A2) (C2)
Note: Award (A2) for 3 correctly placed values, and no extras (4 need not be seen), (A1) for 2 correctly placed values, (A0) for 1 or no correctly placed values.[2 marks]
18 + 10 + 6 = 30 (M1)
= 4 (A1) (C2)[2 marks]
\({\text{P}}(A|B) = \frac{4}{{10}}\left( {\frac{2}{5},{\text{ }}0.4,{\text{ }}40{\text{ }}\% } \right)\) (A1)(ft)(A1) (C2)
Note: Award (A1)(ft) for their numerator from part (b), (A1) for denominator.[2 marks]
Question
\(U\) is the set of all the positive integers less than or equal to \(12\).
\(A\) , \(B\) and \(C\) are subsets of \(U\) .
\[A = \{ 1{\text{, }}2{\text{, }}3{\text{, }}4{\text{, }}6{\text{, }}12\} \]\[B = \{ {\text{odd integers}}\} \]\[C = \{ 5{\text{, }}6{\text{, }}8\} \]
Write down the number of elements in \(A \cap C\) .[1]
List the elements of \(B\) .[1]
Complete the following Venn diagram with all the elements of \(U\) .
[4]
Answer/Explanation
Markscheme
\(1\) (one) (A1) (C1)
Note: \(6\), \(\{6\} \) or \(\{1\} \) earns no marks.[1 mark]
\(1\), \(3\), \(5\), \(7\), \(9\), \(11\) (A1) (C1)
Note: Do not penalise if braces, parentheses or brackets are seen.[1 mark]
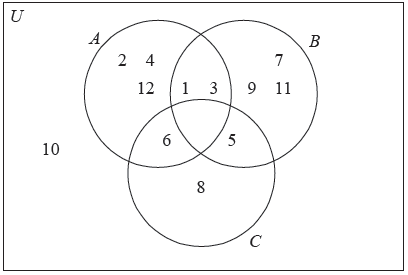(A1)(A1)(ft)(A1)(ft)(A1)(ft) (C4)
Notes: Award (A1) for the empty set \(A \cap B \cap C\) .
Award (A1)(ft) for the correct placement of \(6\), \(5\), \(1\) and \(3\).
Award (A1)(ft) for the correct placement of \(2\), \(4\), \(12\), \(7\), \(9\), \(11\), \(8\).
Award (A1)(ft) for the correct placement of \(10\).
Follow through from part (b).[4 marks]
Question
A group of 33 people was asked about the passports they have. 21 have Australian passports, 15 have British passports and 3 have neither.
A group of 33 people was asked about the passports they have. 21 have Australian passports, 15 have British passports and 3 have neither.
Find the number that have both Australian and British passports.[2]
In the Venn diagram below, set A represents the people in the group with Australian passports and set B those with British passports.
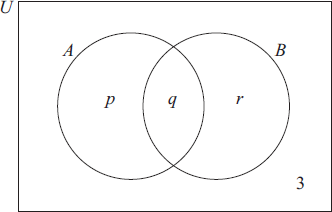
Write down the value of
(i) q ;
(ii) p and of r .[2]
In the Venn diagram below, set A represents the people in the group with Australian passports and set B those with British passports.
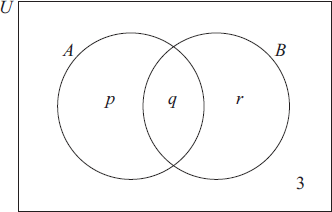
Find \(n(A \cup B’)\) .[2]
Answer/Explanation
Markscheme
\(21 + 15 + 3 – 33\) or equivalent (M1)
Note: Award (M1) for correct use of all four numbers.
\( = 6\) (A1) (C2)[2 marks]
(i) q = 6 (A1)(ft)
(ii) p =15, r = 9 (A1)(ft) (C2)
Note: Follow through from their answer to part (a).[2 marks]
15 + 6 + 3 (M1)
Note: Award (M1) for their figures seen in a correct calculation:
15 + 6 + 3 or 21 + 3 or 33 − 9
= 24 (A1)(ft) (C2)
Note: Follow through from parts (a) and (b) or from values shown on Venn diagram.[2 marks]
Question
Music lessons in Piano (P), Violin (V) and Flute (F) are offered to students at a school.
The Venn diagram shows the number of students who learn each kind of instrument.
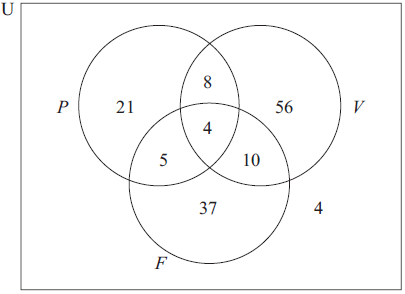
Write down the total number of students in the school.[1]
Write down the number of students who
(i) learn violin only;
(ii) learn piano or flute or both;
(iii) do not learn flute.[3]
Explain, in words, the meaning of the part of the diagram that represents the set \(P \cap F’\).[2]
Answer/Explanation
Markscheme
145 (A1) (C1)[1 mark]
(i) 56 (A1)
(ii) 85 (A1)
(iii) 89 (A1) (C3)[3 marks]
The students who learn the piano and do not learn the flute. (A1)(A1) (C2)
Notes: Award (A1) for students who learn piano, not flute, (A1) for and (accept but). Accept correct alternative statements. Accept “The number of students who learn the piano and do not learn the flute”.[2 marks]
Question
\(U = \{ x|x{\text{ is an integer, }}2 < x < 10\}\)
A and B are subsets of U such that A = {multiples of 3}, B = {factors of 24}.
List the elements of
(i) U ;
(ii) B .[2]
Write down the elements of U on the Venn diagram.
[3]
Write down \(n (A \cap B)\).[1]
Answer/Explanation
Markscheme
(i) 3, 4, 5, 6, 7, 8, 9 (A1)
(ii) 3, 4, 6, 8 (A1)(ft) (C2)
Notes: Follow through from part (a)(i).[2 marks]
(A1)(ft) for their 3, 6
(A1)(ft) for their 4, 8, 9
(A1)(ft) for their 5, 7 (A1)(ft)(A1)(ft)(A1)(ft) (C3)
Note: Follow through from their universal set and set B in part (a).[3 marks]
2 (A1)(ft) (C1)
Note: Follow through from their Venn diagram.[1 mark]
Question
\(U\) is the set of positive integers less than or equal to \(10\).
\(A\), \(B\) and \(C\) are subsets of \(U\).
\(A = \left\{ {{\text{even integers}}} \right\}\)
\(B = \left\{ {{\text{multiples of }}3} \right\}\)
\(C = \left\{ {6,{\text{ }}7,{\text{ }}8,{\text{ }}9} \right\}\)
List the elements of \(A\).[1]
List the elements of \(B\).[1]
Complete the Venn diagram with all the elements of \(U\).
[4]
Answer/Explanation
Markscheme
\(2, 4, 6, 8, 10\) (A1) (C1)
Note: Do not penalize the use of \(\left\{ {{\text{ }}} \right\}\).[1 mark]
\(3, 6, 9\) (A1) (C1)
Note: Do not penalize the use of \(\left\{ {{\text{ }}} \right\}\).
Follow through from part (a) only if their \({\text{U}}\) is listed.[1 mark]
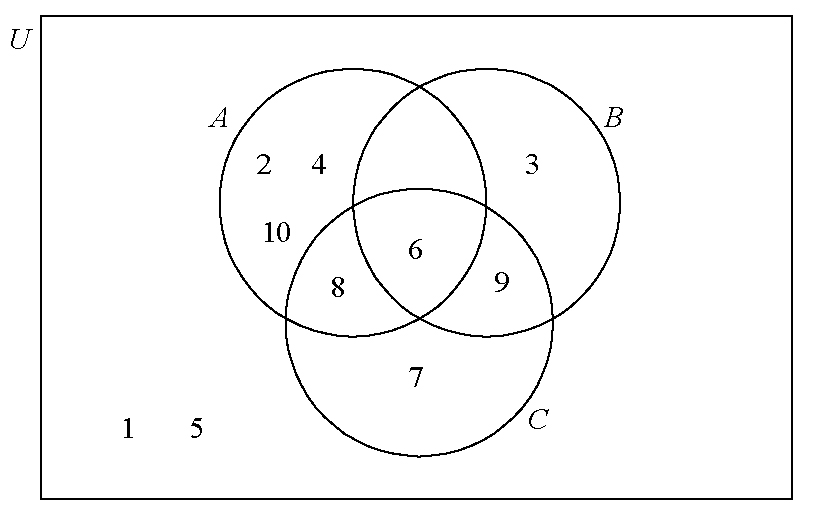(A1)(ft)(A1)(ft)(A1)(ft)(A1)(ft) (C4)
Notes: Award (A1)(ft) for the correct placement of \(6\).
Award (A1)(ft) for the correct placement of \(8\) and \(9\) and the empty region.
Award (A1)(ft) for the correct placement of \(2\), \(4\), \(3\), \(7\), and \(10\).
Award (A1)(ft) for the correct placement of \(1\) and \(5\).
If an element is in more than one region, award (A0) for that element.
Follow through from their answers to parts (a) and (b).[4 marks]
Question
The following Venn diagram shows the relationship between the sets of numbers
\[\mathbb{N},{\text{ }}\mathbb{Z}{\text{, }}\mathbb{Q}{\text{ and }}\mathbb{R}{\text{.}}\]
The number –3 belongs to the set of \(\mathbb{Z}{\text{, }}\mathbb{Q}\) and \(\mathbb{R}\), but not \(\mathbb{N}\), and is placed in the appropriate position on the Venn diagram as an example.
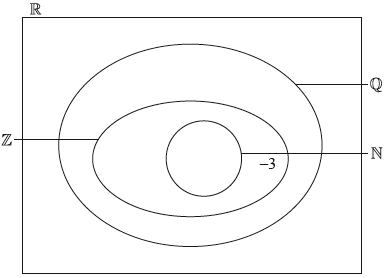
Write down the following numbers in the appropriate place in the Venn diagram.
4[1]
\(\frac{1}{3}\)[1]
\(\pi \)[1]
\(0.38\)[1]
\(\sqrt 5 \)[1]
\(-0.25\)[1]
Answer/Explanation
Markscheme
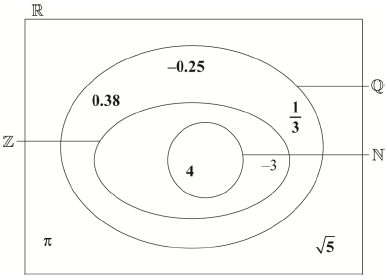(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.[1 mark]
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.[1 mark]
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.[1 mark]
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.[1 mark]
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.[1 mark]
(A1)(A1)(A1)(A1)(A1)(A1) (C6)
Note: Award (A1) for each number correctly placed.
Award (A0) for any entry in more than one region.[1 mark]
Question
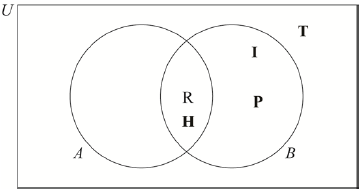
Tuti has the following polygons to classify: rectangle (R), rhombus (H), isosceles triangle (I), regular pentagon (P), and scalene triangle (T).
In the Venn diagram below, set \(A\) consists of the polygons that have at least one pair of parallel sides, and set \(B\) consists of the polygons that have at least one pair of equal sides.
Complete the Venn diagram by placing the letter corresponding to each polygon in the appropriate region. For example, R has already been placed, and represents the rectangle.[3]
State which polygons from Tuti’s list are elements of
(i) \(A \cap B\);
(ii) \((A \cup B)’\).[3]
Answer/Explanation
Markscheme
(A3) (C3)
Note: Award (A3) if all four letters placed correctly,
(A2) if three letters are placed correctly,
(A1) if two letters are placed correctly.
(i) Rhombus and rectangle OR H and R (A1)(ft)
(ii) Scalene triangle OR T (A2)(ft) (C3)
Notes: Award (A1) for a list R, H, I, P seen (identifying the union).
Follow through from their part (a).
Question
Aleph has an unbiased cubical (six faced) die on which are written the numbers
1 , 2 , 3 , 4 , 5 and 6.
Beth has an unbiased tetrahedral (four faced) die on which are written the numbers
2 , 3 , 5 and 7.
Complete the Venn diagram with the numbers written on Aleph’s die (\(A\)) and Beth’s die (\(B\)).
[2]
Find \(n(B \cap A’)\).[2]
Aleph and Beth are each going to roll their die once only. Shin says the probability that each die will show the same number is \(\frac{1}{8}\).
Determine whether Shin is correct. Give a reason.[2]
Answer/Explanation
Markscheme
(A1)(A1) (C2)
Note: Award (A1) for 2, 3, 5 in intersection, (A1) for 1, 4, 6, 7 correctly placed.
\(1\) (M1)(A1)(ft) (C2)
Notes: Award (M1)(A0) for listing the elements of their set \(B \cap A’\);shading the correct region on diagram; or an answer of \(1/7\) with a correct Venn diagram. Follow through from part (a).
Correct, from \((2,{\text{ }}2){\text{ }}(3,{\text{ }}3)\) and \((5,{\text{ }}5)\) on sample space
OR
Correct, from a labelled tree diagram
OR
Correct, from a sample space diagram
OR
Correct, from \(3 \times \frac{1}{4} \times \frac{1}{6}\;\;\;\)(or equivalent) (A1)(ft)(R1) (C2)
Notes: Do not award (A1)(ft)(R0). Award (R1) for a consistent reason with their part (a). Follow through from part (a).
Question
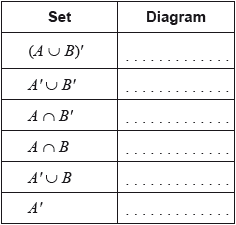
Consider the following Venn diagrams. Each diagram is shaded differently.
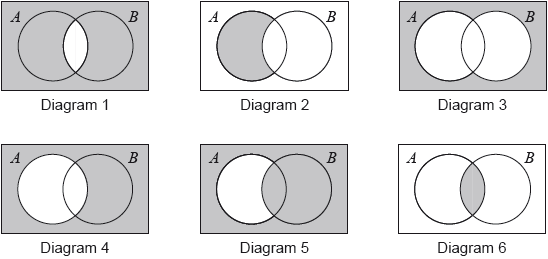
In the following table there are six sets. Each of these sets corresponds to the shaded region of one of the Venn diagrams. In the correct space, write the number of the diagram that corresponds to that set.
Answer/Explanation
Markscheme
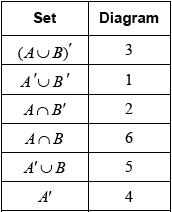(A6)(C6)
Note: Award (A1) for each correct entry.
Question
All the children in a summer camp play at least one sport, from a choice of football (\(F\)) or basketball (\(B\)). 15 children play both sports.
The number of children who play only football is double the number of children who play only basketball.
Let \(x\) be the number of children who play only football.
There are 120 children in the summer camp.
Write down an expression, in terms of \(x\), for the number of children who play only basketball.[1]
Complete the Venn diagram using the above information.
[2]
Find the number of children who play only football.[2]
Write down the value of \(n(F)\).[1]
Answer/Explanation
Markscheme
\(\frac{1}{2}x\) (A1) (C1)[1 mark]
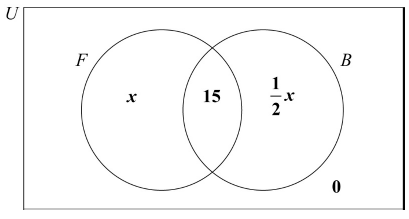(A1)(A1)(ft) (C2)
Notes: Award (A1) for 15 placed in the correct position, award (A1)(ft) for \(x\) and their \(\frac{1}{2}x\) placed in the correct positions of diagram. Do not penalize the absence of 0 inside the rectangle and award at most (A1)(A0) if any value other than 0 is seen outside the circles. Award at most (A1)(A0) if 35 and 70 are seen instead of \(x\) and their \(\frac{1}{2}x\).[2 marks]
\(x + \frac{1}{2}x + 15 = 120\) or equivalent (M1)
Note: Award (M1) for adding the values in their Venn and equating to 120 (or equivalent).
\((x = ){\text{ }}70\) (A1)(ft) (C2)
Note: Follow through from their Venn diagram, but only if the answer is a positive integer and \(x\) is seen in their Venn diagram.[2 marks]
85 (A1)(ft) (C1)
Note: Follow through from their Venn diagram and their answer to part (c), but only if the answer is a positive integer and less than 120.[1 mark]
Question
Rosewood College has 120 students. The students can join the sports club (\(S\)) and the music club (\(M\)).
For a student chosen at random from these 120, the probability that they joined both clubs is \(\frac{1}{4}\) and the probability that they joined the music club is\(\frac{1}{3}\).
There are 20 students that did not join either club.
Complete the Venn diagram for these students.
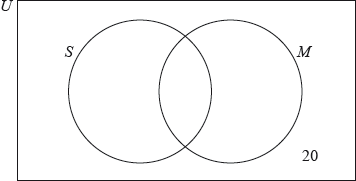[2]
One of the students who joined the sports club is chosen at random. Find the probability that this student joined both clubs.[2]
Determine whether the events \(S\) and \(M\) are independent.[2]
Answer/Explanation
Markscheme
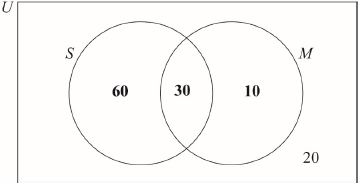(A1)(A1) (C2)
Note: Award (A1) for 30 in correct area, (A1) for 60 and 10 in the correct areas.[2 marks]
\(\frac{{30}}{{90}}{\text{ }}\left( {\frac{1}{3},{\text{ }}0.333333 \ldots ,{\text{ }}33.3333 \ldots \% } \right)\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A1)(ft) for correct numerator of 30, (A1)(ft) for correct denominator of 90. Follow through from their Venn diagram.[2 marks]
\({\text{P}}(S) \times {\text{P}}(M) = \frac{3}{4} \times \frac{1}{3} = \frac{1}{4}\) (R1)
Note: Award (R1) for multiplying their by \(\frac{1}{3}\).
therefore the events are independent \(\left( {{\text{as P}}(S \cap M) = \frac{1}{4}} \right)\) (A1)(ft) (C2)
Note: Award (R1)(A1)(ft) for an answer which is consistent with their Venn diagram.
Do not award (R0)(A1)(ft).
Do not award final (A1) if \({\text{P}}(S) \times {\text{P}}(M)\) is not calculated. Follow through from part (a).[2 marks]
Question
Consider the following Venn diagrams.
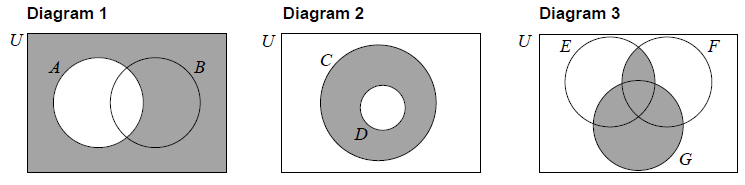
Write down an expression, in set notation, for the shaded region represented by Diagram 1.[1]
Write down an expression, in set notation, for the shaded region represented by Diagram 2.[1]
Write down an expression, in set notation, for the shaded region represented by Diagram 3.[2]
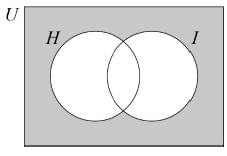
Shade, on the Venn diagram, the region represented by the set \(\left( {H \cup I} \right)’\).
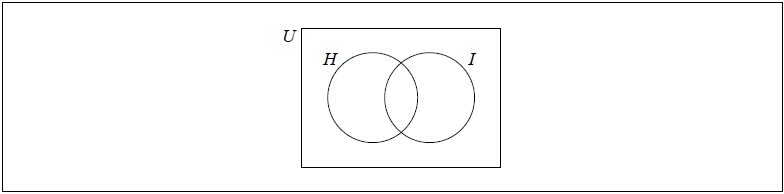[1]
Shade, on the Venn diagram, the region represented by the set \(J \cap K\).
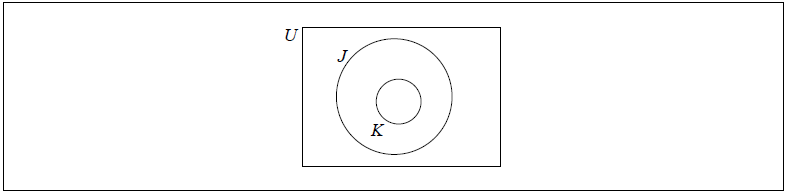[1]
Answer/Explanation
Markscheme
A’ (A1)
Note: Accept alternative set notation for complement such as U − A.[1 mark]
\(C \cap D’\) OR \(D’ \cap C\) (A1)
Note: Accept alternative set notation for complement.[1 mark]
\(\left( {E \cap F} \right) \cup G\) OR \(G \cup \left( {E \cap F} \right)\) (A2) (C4)
Note: Accept equivalent answers, for example \(\left( {E \cup G} \right) \cap \left( {F \cup G} \right)\).[2 marks]
(A1)[1 mark]
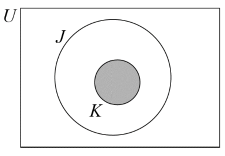(A1) (C2)[1 mark]