Question
A weighted die has 2 red faces, 3 green faces and 1 black face. When the die is thrown, the black face is three times as likely to appear on top as one of the other five faces. The other five faces have equal probability of appearing on top.
The following table gives the probabilities.
Find the value of
(i) m;
(ii) n.[2]
The die is thrown once.
Given that the face on top is not red, find the probability that it is black.[2]
The die is now thrown twice.
Calculate the probability that black appears on top both times.[2]
Answer/Explanation
Markscheme
(i) m = 1 (A1)
(ii) n = 3 (A1) (C2)
Note: Award (A0)(A1)(ft) for \(m = \frac{1}{8}, n = \frac{3}{8}\).
Award (A0)(A1)(ft) for m = 3, n = 1.[2 marks]
\({\rm{P}}(B/R’) = \frac{{\frac{3}{8}}}{{\frac{6}{8}}} = \frac{3}{6}\left( {\frac{1}{2},50\% ,0.5} \right)\) (M1)(A1)(ft) (C2)
Note: Award (M1) for correctly substituted conditional probability formula or for 6 seen as part of denominator.[2 marks]
\({\rm{P}}(B,B) = \frac{3}{8} \times \frac{3}{8} = \frac{9}{{64}}(0.141)\) (M1)(A1)(ft) (C2)
Note: Award (M1) for product of two correct fractions, decimals or percentages.
(ft) from their answer to part (a) (ii).[2 marks]
Question
A class consists of students studying Spanish or French or both. Fifteen students study Spanish and twelve study French.
The probability that a student studies French given that she studies Spanish is \(\frac{{7}}{{15}}\).
Draw a Venn diagram in the space below to illustrate this information.[3]
Find the probability that a student studies Spanish given that she studies one language only.[3]
Answer/Explanation
Markscheme
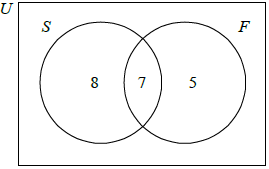(A1)(A1)(A1) (C3)
Note: Award (A1) for a labeled Venn diagram with appropriate sets.
(A1) for 7, (A1) for 8 and 5.[3 marks]
\({\text{P (Spanish / one language only)}} = \frac{{\frac{8}{{20}}}}{{\frac{8}{{20}} + \frac{5}{{20}}}}\) (M1)(A1)(ft)
Note: Award (M1) for substituted conditional probability formula, (A1) for correct substitution. Follow through from their Venn diagram.
\( = \frac{8}{{13}}(0.615,{\text{ }}61.5\% )\) (A1)(ft)
OR
\({\text{P}}{\text{ (Spanish / one language only)}} = \frac{8}{{8 + 5}}\) (A1)(ft)(M1)
Note: Award (A1) for their correct numerator, (M1) for correct recognition of regions. Follow through from their Venn diagram.
\( = \frac{8}{{13}}(0.615,{\text{ }}61.5\% )\) (A1)(ft) (C3)[3 marks]
Question
In a research project on the relation between the gender of 150 science students at college and their degree subject, the following set of data is collected.
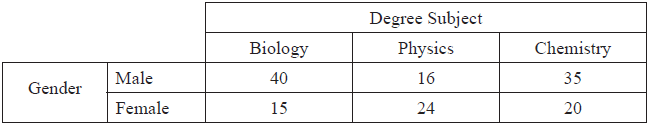
Find the probability that a student chosen at random is male.[2]
Find the probability that a student chosen at random is either male or studies Chemistry.[2]
Find the probability that a student chosen at random studies Physics, given that the student is male.[2]
Answer/Explanation
Markscheme
\( = \frac{{91}}{{150}}(0.607,{\text{ }}60.6\,\% ,{\text{ }}60.7\,\% )\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\( = \frac{{111}}{{150}}\left( {\frac{{37}}{{50}},{\text{ }}0.74,{\text{ }}74\,\% } \right)\) (A1)(ft)(A1) (C2)
Note: Award (A1)(ft) for their numerator in (a) +20 provided the final answer is not greater than 1. (A1) for denominator.[2 marks]
\(\frac{{16}}{{91}}(0.176,{\text{ }}17.6\,\% )\) (A1)(A1)(ft) (C2)
Note: Award (A1) for numerator and (A1)(ft) for denominator. Follow through from their numerator in (a) provided answer is not greater than 1.[2 marks]
Question
A group of 30 students were asked about their favourite topping for toast.
18 liked peanut butter (A)
10 liked jam (B)
6 liked neither
Show this information on the Venn diagram below.
[2]
Find the number of students who like both peanut butter and jam.[2]
Find the probability that a randomly chosen student from the group likes peanut butter, given that they like jam.[2]
Answer/Explanation
Markscheme
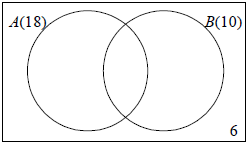OR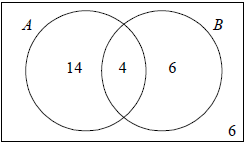 
(A2) (C2)
Note: Award (A2) for 3 correctly placed values, and no extras (4 need not be seen), (A1) for 2 correctly placed values, (A0) for 1 or no correctly placed values.[2 marks]
18 + 10 + 6 = 30 (M1)
= 4 (A1) (C2)[2 marks]
\({\text{P}}(A|B) = \frac{4}{{10}}\left( {\frac{2}{5},{\text{ }}0.4,{\text{ }}40{\text{ }}\% } \right)\) (A1)(ft)(A1) (C2)
Note: Award (A1)(ft) for their numerator from part (b), (A1) for denominator.[2 marks]
Question
Let \({\text{P}}(A) = 0.5\), \({\text{P}}(B) = 0.6\) and \({\text{P}}(A \cup B) = 0.8\).
Find \({\text{P}}(A \cap B)\).[2]
Find \({\text{P}}(A|B)\).[2]
Decide whether A and B are independent events. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
\(0.8 = 0.5 + 0.6 – {\text{P}}(A \cap B)\) (M1)
\({\text{P}}(A \cap B) = 0.3\) (A1) (C2)
Note: Award (M1) for correct substitution, (A1) for correct answer.[2 marks]
\({\text{P}}(A|B) = \frac{{0.3}}{{0.6}}\) (M1)
= 0.5 (A1)(ft) (C2)
Note: Award (M1) for correct substitution in conditional probability formula. Follow through from their answer to part (a), provided probability is not greater than one.[2 marks]
\({\text{P}}(A \cap B) = {\text{P}}(A) \times {\text{P}}(B)\) or 0.3 = 0.5 × 0.6 (R1)
OR
\({\text{P}}(A|B) = {\text{P}}(A)\) (R1)
they are independent. (Yes) (A1)(ft) (C2)
Note: Follow through from their answers to parts (a) or (b).
Do not award (R0)(A1).[2 marks]
Question
A survey was carried out in a group of 200 people. They were asked whether they smoke or not. The collected information was organized in the following table.
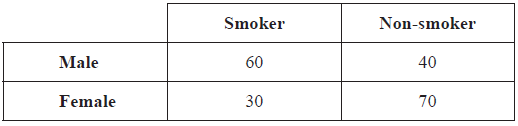
One person from this group is chosen at random.
Write down the probability that this person is a smoker.[2]
Write down the probability that this person is male given that they are a smoker.[2]
Find the probability that this person is a smoker or is male.[2]
Answer/Explanation
Markscheme
\(\frac{{90}}{{200}}(0.45,{\text{ }}45{\text{ }}\% )\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{{60}}{{90}}(0.\bar 6,{\text{ }}0.667,{\text{ }}66.\bar 6{\text{ }}\% ,{\text{ }}66.6 \ldots {\text{ }}\% ,{\text{ }}66.7{\text{ }}\% )\) (A1)(A1)(ft) (C2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator, follow through from their numerator in part (a). Last mark is lost if answer is not a probability.[2 marks]
\(\frac{{90}}{{200}} + \frac{{100}}{{200}} – \frac{{60}}{{200}}\) (M1)
Note: Award (M1) for correct substitution in the combined events formula. Follow through from their answer to part (a).
\( = \frac{{130}}{{200}}(0.65,{\text{ }}65{\text{ }}\% )\) (A1)(ft)
OR
\(\frac{{60}}{{200}} + \frac{{40}}{{200}} + \frac{{30}}{{200}}\) (M1)
Note: Award (M1) for adding the correct fractions.
\( = \frac{{130}}{{200}}(0.65,{\text{ }}65{\text{ }}\% )\) (A1)
OR
\(1 – \frac{{70}}{{200}}\) (M1)
Note: Award (M1) for subtraction of correct fraction from 1.
\( = \frac{{130}}{{200}}(0.65,{\text{ }}65{\text{ }}\% )\) (A1) (C2)[2 marks]
Question
A survey was carried out at an international airport. A number of travellers were interviewed and asked for their flight destinations. The results are shown in the table below.
One traveller is to be chosen at random from all those interviewed.
Find the probability that this traveller was going to Africa.[2]
One female traveller is to be chosen at random from all those interviewed.
Find the probability that this female traveller was going to Asia.[2]
One traveller is to be chosen at random from those not going to America.
Find the probability that the chosen traveller is female.[2]
Answer/Explanation
Markscheme
\(\frac{{108}}{{250}}{\text{ }}\left( {\frac{{54}}{{125}}{\text{, }}0.432{\text{, }}43.2\% } \right)\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{{25}}{{106}}{\text{ }}\left( {0.236{\text{, }}23.6\% } \right)\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{{71}}{{170}}{\text{ }}\left( {0.418{\text{, }}41.8\% } \right)\) (A1)(A1) (C2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
Question
A bag contains 7 red discs and 4 blue discs. Ju Shen chooses a disc at random from the bag and removes it. Ramón then chooses a disc from those left in the bag.
Write down the probability that
(i) Ju Shen chooses a red disc from the bag;
(ii) Ramón chooses a blue disc from the bag, given that Ju Shen has chosen a red disc;
(iii) Ju Shen chooses a red disc and Ramón chooses a blue disc from the bag.[3]
Find the probability that Ju Shen and Ramón choose different coloured discs from the bag.[3]
Answer/Explanation
Markscheme
(i) \(\frac{7}{{11}}\) (\(0.636\), \(63.6\% \)) (\(0.636363 \ldots \)) (A1) (C1)
(ii) \(\frac{4}{{10}}\) \(\left( {\frac{2}{5}{\text{, }}0.4{\text{, }}40\% } \right)\) (A1) (C1)
(iii) \(\frac{{28}}{{110}}\) \(\left( {\frac{{14}}{{55}}{\text{, }}0.255{\text{, }}25.5\% } \right)\) \(0.254545 \ldots \) (A1)(ft) (C1)
Note: Follow through from the product of their answers to parts (a) (i) and (ii).[3 marks]
\(\frac{{28}}{{110}} + \left( {\frac{4}{{11}} \times \frac{7}{{10}}} \right)\) OR \(2 \times \frac{{28}}{{110}}\) (M1)(M1)
Notes: Award (M1) for using their \(\frac{{28}}{{110}}\) as part of a combined probability expression. (M1) for either adding \({\frac{4}{{11}} \times \frac{7}{{10}}}\) or for multiplying by 2.
\( = \frac{{56}}{{110}}\) \(\left( {\frac{{28}}{{55}}{\text{, }}0.509{\text{, }}50.9\% } \right)\) (\(0.509090 \ldots \)) (A1)(ft) (C3)
Note: Follow through applies from their answer to part (a) (iii) and only when their answer is between 0 and 1.[3 marks]
Question
Merryn plans to travel to a concert tomorrow. Due to bad weather, there is a 60 % chance that all flights will be cancelled tomorrow. If the flights are cancelled Merryn will travel by car.
If she travels by plane the probability that she will be late for the concert is 10 %.
If she travels by car, the probability that she will not be late for the concert is 25 %.
Complete the tree diagram below.
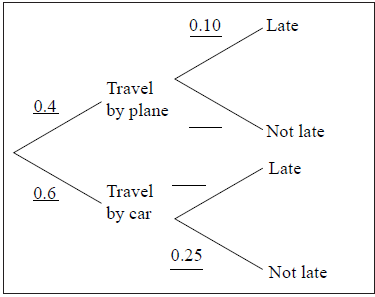[1]
Find the probability that Merryn will not be late for the concert.[3]
Merryn was not late for the concert the next day.
Given that, find the probability that she travelled to the concert by car.[2]
Answer/Explanation
Markscheme
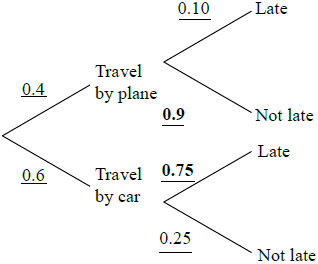(A1) (C1)
Note: Award (A1) for 0.9 and 0.75.[1 mark]
0.4 × 0.9 + 0.6 × 0.25 (M1)(M1)
Note: Award (M1) for their two relevant products, (M1) for adding their two products.
\(0.51\left( {\frac{{51}}{{100}},{\text{ }}51\% } \right)\) (A1)(ft) (C3)
Note: Follow through from their answers to part (a).[3 marks]
\(\frac{{0.6 \times 0.25}}{{0.51}}\) (M1)
Note: Award (M1) for correctly substituted conditional probability formula.
\(0.294\left( {\frac{5}{{17}}{\text{, }}0.294117…} \right)\) (A1)(ft) (C2)
Note: Follow through from their tree diagram and their part (b).[2 marks]
Question
Peter either walks or cycles to work. The probability that he walks is 0.25. If Peter walks to work, the probability that he is late is 0.1. If he cycles to work, the probability that he is late is 0.05. The tree diagram for this information is shown.
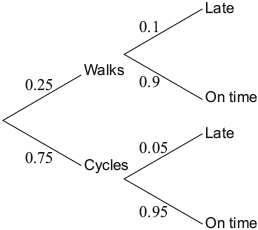
On a day chosen at random, Peter walked to work.
Write down the probability that he was on time.[1]
For a different day, also chosen at random,
find the probability that Peter cycled to work and was late.[2]
For a different day, also chosen at random,
find the probability that, given Peter was late, he cycled to work.[3]
Answer/Explanation
Markscheme
\(0.9\) (A1) (C1)
\(0.75 \times 0.05\) (M1)
\( = 0.0375\;\;\;\left( {\frac{3}{{80}},{\text{ 3,75% }}} \right)\) (A1) (C2)
\(\frac{{0.75 \times 0.05}}{{0.75 \times 0.05 + 0.25 \times 0.1}}\) (M1)(M1)
Note: Award (M1) for their correct numerator, (M1) for their correct denominator, ie, \(\left( {\frac{{{\text{their (b)}}}}{{{\text{their (b)}} + 0.25 \times 0.1}}} \right)\).
Do not award (M1) for their \(0.0375\) or \(0.0625\) if not a correct part of a fraction.
\( = 0.6\;\;\;\left( {\frac{3}{5},{\text{ }}60\% } \right)\) (A1)(ft) (C3)
Note: Follow through from part (b).
Question
Dune Canyon High School organizes its school year into three trimesters: fall/autumn (\(F\)), winter (\(W\)) and spring (\(S\)). The school offers a variety of sporting activities during and outside the school year.
The activities offered by the school are summarized in the following Venn diagram.
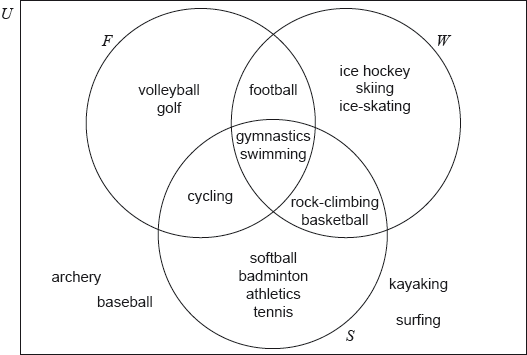
Write down the number of sporting activities offered by the school during its school year.[1]
Determine whether rock-climbing is offered by the school in the fall/autumn trimester.[1]
Write down the elements of the set \(F \cap W’\);[1]
Write down \(n(W \cap S)\).[1]
Write down, in terms of \(F\), \(W\) and \(S\), an expression for the set which contains only archery, baseball, kayaking and surfing.[2]
Answer/Explanation
Markscheme
15 (A1) (C1)[1 mark]
no (A1) (C1)
Note: Accept “it is only offered in Winter and Spring”.[1 mark]
volleyball, golf, cycling (A1) (C1)
Note: Responses must list all three sports for the (A1) to be awarded.[1 mark]
4 (A1) (C1)[1 mark]
\((F \cup W \cup S)’\)\(\,\,\,\)OR\(\,\,\,\)\(F’ \cap W’ \cap S’\) (or equivalent) (A2) (C2)[2 marks]