Question
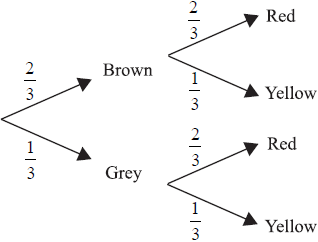
Neil has three dogs. Two are brown and one is grey. When he feeds the dogs, Neil uses three bowls and gives them out randomly. There are two red bowls and one yellow bowl. This information is shown on the tree diagram below.
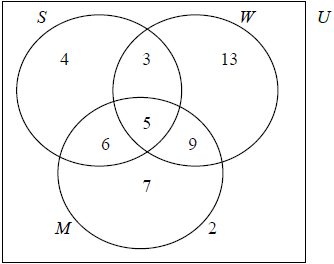
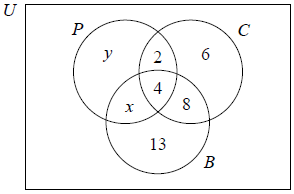
There are 49 mice in a pet shop.
30 mice are white.
27 mice are male.
18 mice have short tails.
8 mice are white and have short tails.
11 mice are male and have short tails.
7 mice are male but neither white nor short-tailed.
5 mice have all three characteristics and
2 have none.
Copy the diagram below to your examination script.

One of the dogs is chosen at random.
(i) Find P (the dog is grey and has the yellow bowl).
(ii) Find P (the dog does not get the yellow bowl).[3]
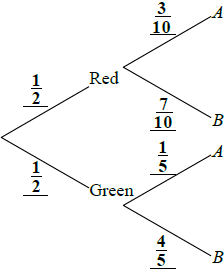
Neil often takes the dogs to the park after they have eaten. He has noticed that the grey dog plays with a stick for a quarter of the time and both brown dogs play with sticks for half of the time. This information is shown on the tree diagram below.
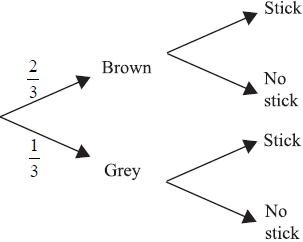
(i) Copy the tree diagram and add the four missing probability values on the branches that refer to playing with a stick.
During a trip to the park, one of the dogs is chosen at random.
(ii) Find P (the dog is grey or is playing with a stick, but not both).
(iii) Find P (the dog is grey given that the dog is playing with a stick).
(iv) Find P (the dog is grey and was fed from the yellow bowl and is not playing with a stick).[9]
Complete the diagram, using the information given in the question.[4]
Find (i) \(n(M \cap W)\)
(ii) \(n(M′ \cup S)\)[3]
Two mice are chosen without replacement.
Find P (both mice are short-tailed).[2]
Answer/Explanation
Markscheme
(i) P (a dog is grey and has the yellow bowl)
\( = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}( = 0.111)\) (M1)(A1)(G2)
The (M1) is for multiplying two values along any branch of the tree.
(ii) P (dog does not get yellow bowl) \( = \frac{2}{3}\) ( = 0.667 (3sf) or 0.6) (A1)[3 marks]
(i) The tree diagram should show the values \(\frac{1}{2},\frac{1}{2}\) for the brown branch and \(\frac{1}{4},\frac{3}{4}\) in the correct positions for the grey branch. (A1)(A1)(ft)
Follow through if the branches are interchanged.
(ii) P (the dog is grey or is playing with a stick, but not both)
\( = \frac{1}{3} \times \frac{3}{4} + \frac{2}{3} \times \frac{1}{2}\) (M1)
\( = \frac{7}{{12}}\) ( = 0.583) (A1)(ft)(G1)
The (M1) is for showing two correct products (whether added or not). Follow through from b(i). Award (M1) for \( \frac{1}{3} + \frac{1}{4}\) (must be a sum).
(iii) P (dog is grey given that it is playing with stick)
\(\frac{{P(G \cap S)}}{{P(S)}} = \frac{{\frac{1}{3} \times \frac{1}{4}}}{{\left( {\frac{2}{3} \times \frac{1}{2}} \right) + \left( {\frac{1}{3} \times \frac{1}{4}} \right)}}\) or \(\frac{1}{{12}}/\frac{5}{{12}}\) (M1)(A1)(ft)
(M1) for substituted conditional probability formula, (A1) for correct substitutions.
\( = \frac{1}{5}\) ( = 0.2) (A1)(ft)(G2)
(iv) P (grey and fed from yellow bowl and not playing with stick) \( = \frac{1}{3} \times \frac{1}{3} \times \frac{3}{4} = \frac{1}{{12}}\) ( = \(\frac{3}{{36}}\) = 0.0833 3sf). (M1)(A1)(ft)(G1)
(M1) is for product of 3 reasonable probability values.[9 marks]
 (A1)(A1)(A1)(ft)(A1)(ft)
(A1)(A1)(A1)(ft)(A1)(ft)
Award (A1) for 2 (must be in a box), (A1) for 7, (A1)(ft) for 6 and 4, (A1)(ft) for 9 and 13. Observe the assignment of (ft) marks strictly here. Example A common error is likely to be 11 instead of 6 (A0). In this case follow through to 4 and 18 (A1)(ft) for the final pair. Here the 4 follows from the total of 27 for n(M).[4 marks]
(i) \(n(M \cap W) = 14\) (A1)(ft)
(ii) \(n(M’ \cup S) = 22 + 11\) OR \(15 + 18\) (A1)(ft)
= 33 (A1)(ft)
Award (A2) if answer 33 is seen. Award (A1) for any of 22, 11, 15 or 18 seen but 33 absent. [3 marks]
P (both mice short-tailed) \( = \frac{{18}}{{49}} \times \frac{{17}}{{48}} = \frac{{306}}{{352}}\) (= 0.130). (M1)(A1)(ft)(G1)
(Allow alternatives such as 153/1176 or 51/392.) Award (M1) for any of \(\frac{{18}}{{49}}\) and \(\frac{{17}}{{48}}\) or \(\frac{{18}}{{49}} \times \frac{{17}}{{49}}\) or \(\frac{{18}}{{49}} + \frac{{17}}{{48}}\) seen.[2 marks]
Question
When Geraldine travels to work she can travel either by car (C), bus (B) or train (T). She travels by car on one day in five. She uses the bus 50 % of the time. The probabilities of her being late (L) when travelling by car, bus or train are 0.05, 0.12 and 0.08 respectively.
It is not necessary to use graph paper for this question.
Copy the tree diagram below and fill in all the probabilities, where NL represents not late, to represent this information.
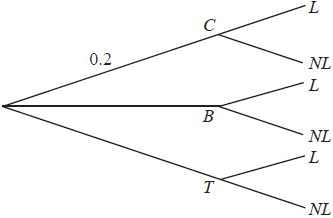 [5]
[5]
Find the probability that Geraldine travels by bus and is late.[1]
Find the probability that Geraldine is late.[3]
Find the probability that Geraldine travelled by train, given that she is late.[3]
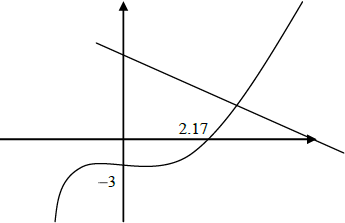
Sketch the curve of the function \(f (x) = x^3 − 2x^2 + x − 3\) for values of \(x\) from −2 to 4, giving the intercepts with both axes.[3]
On the same diagram, sketch the line \(y = 7 − 2x\) and find the coordinates of the point of intersection of the line with the curve.[3]
Find the value of the gradient of the curve where \(x = 1.7\) .[2]
Answer/Explanation
Markscheme
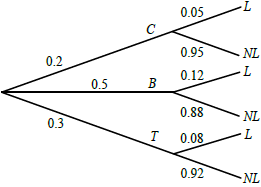
Award (A1) for 0.5 at B, (A1) for 0.3 at T, then (A1) for each correct pair. Accept fractions or percentages. (A5)[5 marks]
0.06 (accept \(0.5 \times 0.12\) or 6%) (A1)(ft)[1 mark]
for a relevant two-factor product, either \(C \times L\) or \(T \times L\) (M1)
for summing three two-factor products (M1)
\((0.2 \times 0.05 + 0.06 + 0.3 \times 0.08)\)
0.094 (A1)(ft)(G2)[3 marks]
\(\frac{{0.3 \times 0.08}}{{0.094}}\) (M1)(A1)(ft)
award (M1) for substituted conditional probability formula seen, (A1)(ft) for correct substitution
= 0.255 (A1)(ft)(G2)[3 marks]
 (G3)[3 marks]
(G3)[3 marks]
line drawn with –ve gradient and +ve y-intercept (G1)
(2.45, 2.11) (G1)(G1)[3 marks]
\(f ‘ (1.7) = 3(1.7)^2 – 4(1.7) + 1\) (M1)
award (M1) for substituting in their \(f’ (x)\)
2.87 (A1)(G2)[2 marks]
Question
A group of 50 students completed a questionnaire for a Mathematical Studies project. The following data was collected.
\(18\) students own a digital camera (D)
\(15\) students own an iPod (I)
\(26\) students own a cell phone (C)
\(1\) student owns all three items
\(5\) students own a digital camera and an iPod but not a cell phone
\(2\) students own a cell phone and an iPod but not a digital camera
\(3\) students own a cell phone and a digital camera but not an iPod
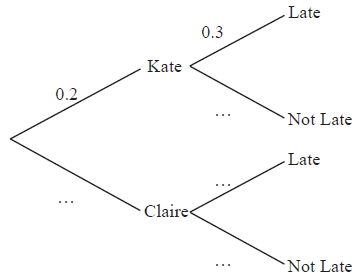
Claire and Kate both wish to go to the cinema but one of them has to stay at home to baby-sit.
The probability that Kate goes to the cinema is \(0.2\). If Kate does not go Claire goes.
If Kate goes to the cinema the probability that she is late home is \(0.3\).
If Claire goes to the cinema the probability that she is late home is \(0.6\).
Represent this information on a Venn diagram.[4]
Calculate the number of students who own none of the items mentioned above.[2]
If a student is chosen at random, write down the probability that the student owns a digital camera only.[1]
If two students are chosen at random, calculate the probability that they both own a cell phone only.[3]
If a student owns an iPod, write down the probability that the student also owns a digital camera.[2]
Copy and complete the probability tree diagram below.
 [3]
[3]
Calculate the probability that
(i) Kate goes to the cinema and is not late;
(ii) the person who goes to the cinema arrives home late.
Answer/Explanation
Markscheme
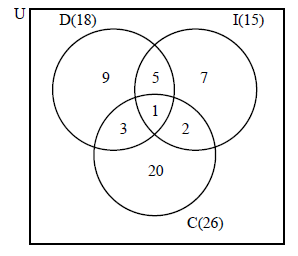 (A1)(A1)(A1)(A1)(ft)
(A1)(A1)(A1)(A1)(ft)
Note: (A1) for rectangle with 3 intersecting circles, (A1) for \(1\), (A1) for \(5\), \(3\), \(2\), (A1)(ft) for \(9\), \(7\), \(20\) if subtraction is carried out, or \(18\), \(15\), \(26\) seen by the letters D, I and C.[4 marks]
\(50 – 47\) (M1)
Note: (M1) for subtracting their value from \(50\).
\( = 3\) (A1)(ft)(G2)[2 marks]
\(\frac{9}{{50}}\) (A1)(ft)[1 mark]
\(\frac{{20}}{{50}} \times \frac{{19}}{{49}}\) (A1)(ft)(M1)
\( = \frac{{38}}{{245}}{\text{ }}\left( {\frac{{380}}{{2450}}{\text{, }}0.155{\text{, }}15.5\% } \right)\) (A1)(ft)(G2)
Notes: (A1)(ft) for correct fractions from their Venn diagram
(M1) for multiplying their fractions
(A1)(ft) for correct answer.[3 marks]
\(\frac{6}{{15}}{\text{ }}\left( {\frac{2}{5}{\text{, }}0.4{\text{, }}40\% } \right)\) (A1)(ft)(A1)(ft)
Note: (A1)(ft) for numerator, (A1)(ft) denominator.[2 marks]
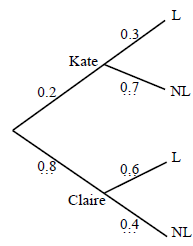 (A1)(A1)(A1)
(A1)(A1)(A1)
Note: (A1) for \(0.8\), (A1) for \(0.7\), (A1) for \(0.6\) and \(0.4\).[3 marks]
(i) \(0.2 \times 0.7 = 0.14\) (M1)(A1)(ft)(G2)
Note: (M1) for multiplying correct numbers.[2 marks]
(ii) \(0.2 \times 0.3 + 0.8 \times 0.6\) (M1)(M1)
\( = 0.54\) (A1)(ft)(G3)
Note: (M1) for each correct product (use candidate’s tree), (A1)(ft) for answer.[3 marks]
Question
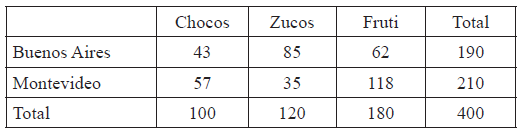
A survey of \(400\) people is carried out by a market research organization in two different cities, Buenos Aires and Montevideo. The people are asked which brand of cereal they prefer out of Chocos, Zucos or Fruti. The table below summarizes their responses.
The following table shows the cost in \({\text{AUD}}\) of seven paperback books chosen at random, together with the number of pages in each book.

One person is chosen at random from those surveyed. Find the probability that this person
(i) does not prefer Zucos;
(ii) prefers Chocos, given that they live in Montevideo.[4]
Two people are chosen at random from those surveyed. Find the probability that they both prefer Fruti.[3]
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
State the null hypothesis.[1]
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
State the number of degrees of freedom.[1]
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
Show that the expected frequency for the number of people who live in Montevideo and prefer Zucos is \(63\).[2]
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
Write down the chi-squared statistic for this data.[2]
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
State whether the market research organization would accept the null hypothesis. Clearly justify your answer.[2]
Plot these pairs of values on a scatter diagram. Use a scale of \(1{\text{ cm}}\) to represent \(50\) pages on the horizontal axis and \(1{\text{ cm}}\) to represent \(1{\text{ AUD}}\) on the vertical axis.[3]
Write down the linear correlation coefficient, \(r\), for the data.[2]
Stephen wishes to buy a paperback book which has \(350\) pages in it. He plans to draw a line of best fit to determine the price. State whether or not this is an appropriate method in this case and justify your answer.[2]
Answer/Explanation
Markscheme
(i) \(\frac{{280}}{{400}}{\text{ }}(0.7{\text{, }}70\% {\text{ or equivalent}})\) (A1)(A1)(G2)
Note: (A1) for correct numerator, (A1) for correct denominator.
(ii) \(\frac{{57}}{{210}}{\text{ }}\left( {\frac{{19}}{{70}}{\text{, }}0.271{\text{, }}27.1\% } \right)\) (A1)(A1)(G2)
Note: (A1) for correct numerator, (A1) for correct denominator.[4 marks]
\(\frac{{180}}{{400}} \times \frac{{179}}{{399}}\) (A1)(M1)
Note: (A1) for correct values seen, (M1) for multiplying their two values, (A1) for correct answer.
\( = \frac{{537}}{{2660}}{\text{ }}( = 0.202)\) (A1)(G3)[3 marks]
\({{\text{H}}_0}\) : ‘the preference of brand of cereal is independent of the city’. (A1)
OR
\({{\text{H}}_0}\) : ‘there is no association between the brand of cereal and city’.[1 mark]
\(df = 2\) (A1)[1 mark]
\(\frac{{210 \times 120}}{{400}}\) (M1)(A1)
Note: (M1) for substituting in correct formula, (A1) for correct values.
\( = 63\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(39.3\) (G2)
Note: Award (G1)(A0)(AP) if answers not to 3 significant figures.[2 marks]
\(p – {\text{value}} < 0.05\) (R1)(ft)
Do not accept \({{{\text{H}}_0}}\) . (A1)(ft)
Notes: Allow ‘Reject \({{{\text{H}}_0}}\) or equivalent’. (ft) from their \({\chi ^2}\) statistic.
Award (R1)(ft) for comparing the appropriate values. (A1)(ft) can be awarded only if the conclusion is valid according to the comparison given. If no reason given or if reason is wrong both marks are lost. Note that (R1)(A0)(ft) can be awarded but (R0)(A1)(ft) cannot.[2 marks]
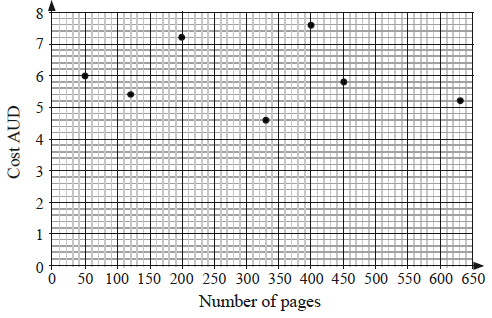 (A1)(A1)(A1)
(A1)(A1)(A1)
Notes: (A1) for label and scales, (A2) for all points correct, (A1) for 5 or 6 correct. Award a maximum of (A2) if points are joined.[3 marks]
\(r = – 0.141\) (G2)
Note: If negative sign is missing award (G1)(G0).[2 marks]
‘The coefficient of correlation is too low, (very) weak (linear) relationship’. (R1)
Not a sensible thing to do, accept ‘no’. (A1)
Note: Do not award (R0)(A1). The correlation coefficient has to be mentioned in their reasoning.[2 marks]
Question
Jorge conducted a survey of \(200\) drivers. He asked two questions:
How long have you had your driving licence?
Do you wear a seat belt when driving?
The replies are summarized in the table below.
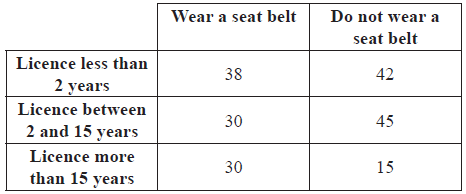
Jorge applies a \({\chi ^2}\) test at the \(5\% \) level to investigate whether wearing a seat belt is associated with the time a driver has had their licence.
(i) Write down the null hypothesis, \({{\text{H}}_0}\).
(ii) Write down the number of degrees of freedom.
(iii) Show that the expected number of drivers that wear a seat belt and have had their driving licence for more than \(15\) years is \(22\), correct to the nearest whole number.
(iv) Write down the \({\chi ^2}\) test statistic for this data.
(v) Does Jorge accept \({{\text{H}}_0}\) ? Give a reason for your answer.[8]
Consider the \(200\) drivers surveyed. One driver is chosen at random. Calculate the probability that
(i) this driver wears a seat belt;
(ii) the driver does not wear a seat belt, given that the driver has held a licence for more than \(15\) years.[4]
Two drivers are chosen at random. Calculate the probability that
(i) both wear a seat belt.
(ii) at least one wears a seat belt.[6]
Answer/Explanation
Markscheme
(i) \({{\text{H}}_0} = \) wearing of a seat belt and the time a driver has held a licence are independent. (A1)
Note: For independent accept ‘not associated’ but do not accept ‘not related’ or ‘not correlated’
(ii) \(2\) (A1)
(iii) \(\frac{{98 \times 45}}{{200}} = 22.05 = 22\) (correct to the nearest whole number) (M1)(A1)(AG)
Note: (M1) for correct formula and (A1) for correct substitution. Unrounded answer must be seen for the (A1) to be awarded.
(iv) \({\chi ^2} = 8.12\) (G2)
Note: For unrounded answer award (G1)(G0)(AP). If formula used award (M1) for correct substituted formula with correct substitution (6 terms) (A1) for correct answer.
(v) “Does not accept \({{\text{H}}_0}\)” (A1)(ft)
\(p{\text{-}}value < 0.05\) (R1)(ft)
Note: Allow “Reject \({{\text{H}}_0}\)” or equivalent. Follow through from their \({\chi ^2}\) statistic. Award (R1)(ft) for comparing the appropriate values. The (A1)(ft) can be awarded only if the conclusion is valid according to the comparison given. If no reason given or if reason is wrong the two marks are lost.[8 marks]
(i) \(\frac{{98}}{{200}}( = 0.49{\text{, }}49\% )\) (A1)(A1)(G2)
Note: (A1) for numerator, (A1) for denominator.
(ii) \(\frac{{15}}{{45}}( = 0.333{\text{, }}33.3\% )\) (A1)(A1)(G2)
Note: (A1) for numerator, (A1) for denominator.[4 marks]
(i) \(\frac{{98}}{{200}} \times \frac{{97}}{{199}} = 0.239{\text{ }}(23.9\% )\) (A1)(M1)(A1)(G3)
Note: (A1) for correct probabilities seen, (M1) for multiplying two probabilities, (A1) for correct answer.
(ii) \(1 – \frac{{102}}{{200}} \times \frac{{101}}{{199}} = 0.741{\text{ }}(74.1\% )\) (M1)(M1)(A1)(ft)(G2)
Note: (M1) for showing the product, (M1) for using the probability of the complement, (A1) for correct answer. Follow through for consistent use of with replacement.
OR
\(\frac{{98}}{{200}} \times \frac{{97}}{{199}} + \frac{{98}}{{200}} \times \frac{{102}}{{199}} + \frac{{102}}{{200}} \times \frac{{98}}{{199}} = 0.741{\text{ }}(74.1\% )\) (M1)(M1)(A1)(ft)(G2)
Note: (M1) for adding three products of fractions (or equivalent), (M1) for using the correct fractions, (A1) for correct answer. Follow through for consistent use of with replacement.[6 marks]
Question
Sharon and Lisa share a flat. Sharon cooks dinner three nights out of ten. If Sharon does not cook dinner, then Lisa does. If Sharon cooks dinner the probability that they have pasta is 0.75. If Lisa cooks dinner the probability that they have pasta is 0.12.
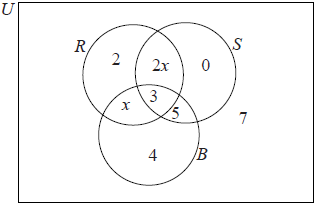
A survey was carried out in a year 12 class. The pupils were asked which pop groups they like out of the Rockers (R), the Salseros (S), and the Bluers (B). The results are shown in the following diagram.
Copy and complete the tree diagram to represent this information.
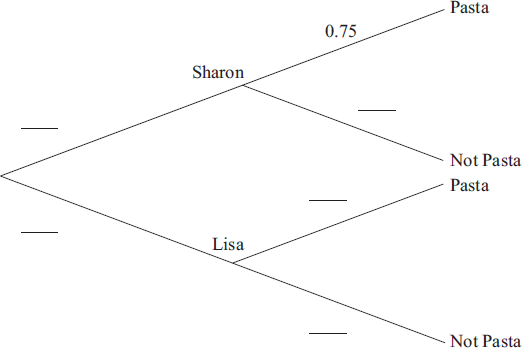 [3]
[3]
Find the probability that Lisa cooks dinner and they do not have pasta.[2]
Find the probability that they do not have pasta.[3]
Given that they do not have pasta, find the probability that Lisa cooked dinner.[3]
Write down \(n(R \cap S \cap B)\).[1]
Find \(n(R’)\).[2]
Describe which groups the pupils in the set \(S \cap B\) like.[2]
Use set notation to describe the group of pupils who like the Rockers and the Bluers but do not like the Salseros.[2]
There are 33 pupils in the class.
Find x.[2]
There are 33 pupils in the class.
Find the number of pupils who like the Rockers.[1]
Answer/Explanation
Markscheme
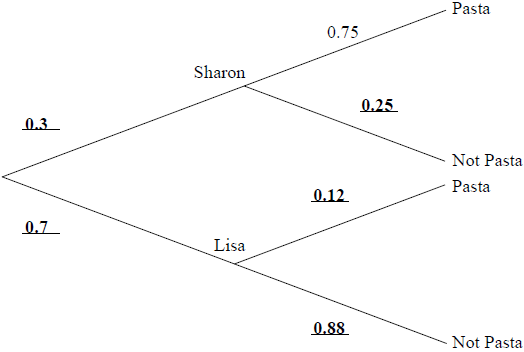
Note: Award (A1) for each correct pair. (A3) [3 marks]
\(0.7 \times 0.88 = 0.616{\text{ }}\left( {\frac{{77}}{{125}},{\text{ }}61.6{\text{ }}\% } \right)\) (M1)(A1)(ft)(G2)
Note: Award (M1) for multiplying the correct probabilities.[2 marks]
\(0.3 \times 0.25 + 0.7 \times 0.88\) (M1)(M1)
Notes: Award (M1) for a relevant two-factor product, could be \(S \times NP\) OR \(L \times NP\).
Award (M1) for summing 2 two-factor products.
\({\text{P}} = 0.691{\text{ }}\left( {\frac{{691}}{{1000}},{\text{ }}69.1{\text{ }}\% } \right)\) (A1)(ft)(G2)
Notes: (ft) from their answer to (b).[3 marks]
\(\frac{{0.616}}{{0.691}}\) (M1)(A1)
Note: Award (M1) for substituted conditional probability formula, (A1) for correct substitution.
\({\text{P}} = 0.891{\text{ }}\left( {\frac{{616}}{{691}},{\text{ }}89.1{\text{ }}\% } \right)\) (A1)(ft)(G2)[3 marks]
3 (A1)[1 mark]
For 5, 4, 7 (0) seen with no extra values (A1)
16 (A1)(G2)[2 marks]
They like (both) the Salseros (S) and they like the Bluers (B) (A1)(A1)
Note: Award (A1) for “and”, (A1) for the correct groups.[2 marks]
\(R \cap B \cap S’\) (A1)(A1)
Note: Award (A1) for \(R \cap B\), (A1) for \( \cap S’\)[2 marks]
\(21+ 3x = 33\) (M1)
\(x = 4\) (A1)(G2)[2 marks]
17 (A1)(ft)[1 mark]
Question
Phoebe chooses a biscuit from a blue tin on a shelf. The tin contains one chocolate biscuit and four plain biscuits. She eats the biscuit and chooses another one from the tin. The tree diagram below represents the situation with the four possible outcomes where A stands for chocolate biscuit and B for plain biscuit.
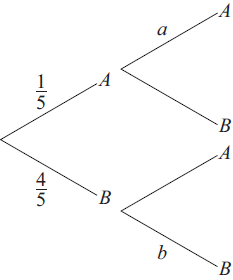
On another shelf there are two tins, one red and one green. The red tin contains three chocolate biscuits and seven plain biscuits and the green tin contains one chocolate biscuit and four plain biscuits. Andrew randomly chooses either the red or the green tin and randomly selects a biscuit.
Write down the value of a.[1]
Write down the value of b.[2]
Find the probability that both biscuits are plain.[3]
Copy and complete the tree diagram below.
 [3]
[3]
Find the probability that he chooses a chocolate biscuit.[3]
Find the probability that he chooses a biscuit from the red tin given that it is a chocolate biscuit.[3]
Answer/Explanation
Markscheme
a = 0 \(\left( {\frac{0}{4}} \right)\) (A1)[1 mark]
\(b = \frac{3}{4}(0.75,{\text{ }}75\% )\) (A2)(G2)[2 marks]
\(\frac{4}{5} \times \frac{3}{4}\) (M1)(A1)
\(\frac{{12}}{{20}}\left( {\frac{3}{5},{\text{ }}0.6,{\text{ 60% }}} \right)\) (A1)(ft)(G2)
Note: Award (M1) for multiplying two probabilities, (A1) for using their probabilities, (A1) for answer.[3 marks]
 (A1)(A1)(A1)
(A1)(A1)(A1)
Note: Award (A1) for each pair.[3 marks]
\(\frac{1}{2} \times \frac{3}{{10}} + \frac{1}{2} \times \frac{1}{5}\) (M1)(M1)
\( = \frac{5}{{20}}\left( {\frac{1}{4},{\text{ }}0.25,{\text{ 25% }}} \right)\) (A1)(ft)(G2)
Note: Award (M1) for two products seen with numbers from the problem, (M1) for adding two products. Follow through from their tree diagram.[3 marks]
\(\frac{{\frac{1}{2} \times \frac{3}{{10}}}}{{\frac{1}{4}}}\) (M1)(A1)
\( = \frac{3}{5}{\text{ }}\left( {0.6,{\text{ 60 }}\% } \right)\) (A1)(ft)(G2)
Note: Award (M1) for substituted conditional probability formula, (A1) for correct substitution.
Follow through from their part (b) and part (c) (i).[3 marks]
Question
Part A
100 students are asked what they had for breakfast on a particular morning. There were three choices: cereal (X) , bread (Y) and fruit (Z). It is found that
10 students had all three
17 students had bread and fruit only
15 students had cereal and fruit only
12 students had cereal and bread only
13 students had only bread
8 students had only cereal
9 students had only fruit
Part B
The same 100 students are also asked how many meals on average they have per day. The data collected is organized in the following table.
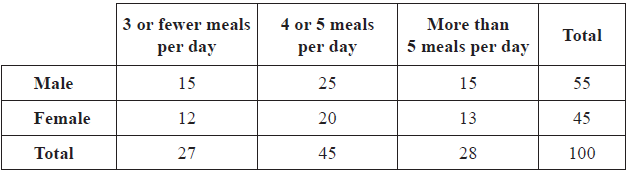
A \({\chi ^2}\) test is carried out at the 5 % level of significance.
Represent this information on a Venn diagram.[4]
Find the number of students who had none of the three choices for breakfast.[2]
Write down the percentage of students who had fruit for breakfast.[2]
Describe in words what the students in the set \(X \cap Y’\) had for breakfast.[2]
Find the probability that a student had at least two of the three choices for breakfast.[2]
Two students are chosen at random. Find the probability that both students had all three choices for breakfast.[3]
Write down the null hypothesis, H0, for this test.[1]
Write down the number of degrees of freedom for this test.[1]
Write down the critical value for this test.[1]
Show that the expected number of females that have more than 5 meals per day is 13, correct to the nearest integer.[2]
Use your graphic display calculator to find the \(\chi _{calc}^2\) for this data.[2]
Decide whether H0 must be accepted. Justify your answer.[2]
Answer/Explanation
Markscheme
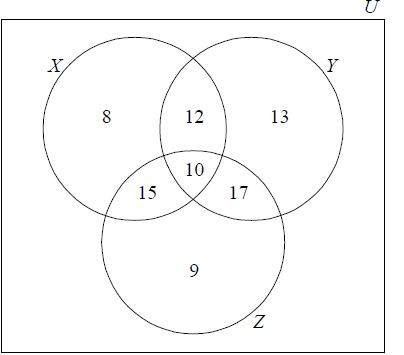
(A1) for rectangle and three intersecting circles
(A1) for 10, (A1) for 8, 13 and 9, (A1) for 12, 15 and 17 (A4)[4 marks]
100 – (9 +12 +13 +15 +10 +17 + 8) =16 (M1)(A1)(ft)(G2)
Note: Follow through from their diagram.[2 marks]
\(\frac{{51}}{{100}}(0.51)\) (A1)(ft)
= 51% (A1)(ft)(G2)
Note: Follow through from their diagram.[2 marks]
Note: The following statements are correct. Please note that the connectives are important. It is not the same (had cereal) and (not bread) and (had cereal) or (not bread). The parentheses are not needed but are there to facilitate the understanding of the propositions.
(had cereal) and (did not have bread)
(had cereal only) or (had cereal and fruit only)
(had either cereal or (fruit and cereal)) and (did not have bread) (A1)(A1)
Notes: If the statements are correct but the connectives are wrong then award at most (A1)(A0). For the statement (had only cereal) and (cereal and fruit) award (A1)(A0). For the statement had cereal and fruit award (A0)(A0).[2 marks]
\(\frac{{54}}{{100}}(0.54,{\text{ 54 % }})\) (A1)(ft)(A1)(ft)(G2)
Note: Award (A1)(ft) for numerator, follow through from their diagram, (A1)(ft) for denominator. Follow through from total or denominator used in part (c).[2 marks]
\(\frac{{10}}{{100}} \times \frac{9}{{99}} = \frac{1}{{110}}(0.00909,{\text{ 0}}{\text{.909 % }})\) (A1)(ft)(M1)(A1)(ft)(G2)
Notes: Award (A1)(ft) for their correct fractions, (M1) for multiplying two fractions, (A1)(ft) for their correct answer. Answer 0.009 with no working receives no marks. Follow through from denominator in parts (c) and (e) and from their diagram.[3 marks]
H0 : The (average) number of meals per day a student has and gender are independent (A1)
Note: For “independent” accept “not associated” but do not accept “not related” or “not correlated”.[1 mark]
2 (A1)[1 mark]
5.99 (accept 5.991) (A1)(ft)
Note: Follow through from their part (b).[1 mark]
\(\frac{{28 \times 45}}{{100}} = 12.6 = 13\) or \(\frac{{28}}{{100}} \times \frac{{25}}{{100}} \times 100 = 12.6 = 13\) (M1)(A1)(AG)
Notes: Award (M1) for correct formula and (A1) for correct substitution. Unrounded answer must be seen for the (A1) to be awarded.[2 marks]
0.0321 (G2)
Note: For 0.032 award (G1)(G1)(AP). For 0.03 with no working award (G0).[2 marks]
0.0321 < 5.99 or 0.984 > 0.05 (R1)
accept H0 (A1)(ft)
Note: If reason is incorrect both marks are lost, do not award (R0)(A1).[2 marks]
Question
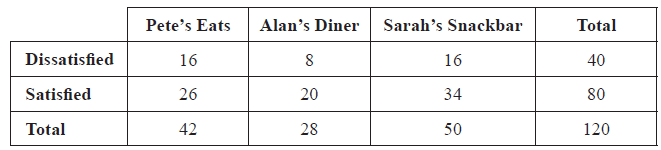
One day the numbers of customers at three cafés, “Alan’s Diner” ( \(A\) ), “Sarah’s Snackbar” ( \(S\) ) and “Pete’s Eats” ( \(P\) ), were recorded and are given below.
17 were customers of Pete’s Eats only
27 were customers of Sarah’s Snackbar only
15 were customers of Alan’s Diner only
10 were customers of Pete’s Eats and Sarah’s Snackbar but not Alan’s Diner
8 were customers of Pete’s Eats and Alan’s Diner but not Sarah’s Snackbar
Some of the customers in each café were given survey forms to complete to find out if they were satisfied with the standard of service they received.
Draw a Venn Diagram, using sets labelled \(A\) , \(S\) and \(P\) , that shows this information.[3]
There were 48 customers of Pete’s Eats that day. Calculate the number of people who were customers of all three cafés.[2]
There were 50 customers of Sarah’s Snackbar that day. Calculate the total number of people who were customers of Alan’s Diner.[3]
Write down the number of customers of Alan’s Diner that were also customers of Pete’s Eats.[1]
Find \(n[(S \cup P) \cap A’]\).[2]
One of the survey forms was chosen at random, find the probability that the form showed “Dissatisfied”;[2]
One of the survey forms was chosen at random, find the probability that the form showed “Satisfied” and was completed at Sarah’s Snackbar;[2]
One of the survey forms was chosen at random, find the probability that the form showed “Dissatisfied”, given that it was completed at Alan’s Diner.[2]
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Write down the null hypothesis, \({{\text{H}}_0}\) , for the \({\chi ^2}\) test.[1]
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Write down the number of degrees of freedom for the test.[1]
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Using your graphic display calculator, find \({\chi ^2}_{calc}\) .[2]
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
State, giving a reason, the conclusion to the test.[2]
Answer/Explanation
Markscheme
(A1) for rectangle and three labelled intersecting circles
(A1) for \(15\), \(27\) and \(17\)
(A1) for \(10\) and \(8\) (A3)[3 marks]
\(48 – (8 +10 +17)\) or equivalent (M1)
\( = 13\) (A1)(ft)(G2)[2 marks]
\(50 – (27 +10 +13)\) (M1)
Note: Award (M1) for working seen.
\( = 0\) (A1)
number of elements in A \(= 36\) (A1)(ft)(G3)
Note: Follow through from (b).[3 marks]
\(21\) (A1)(ft)
Note: Follow through from (b) even if no working seen.[1 mark]
\(54\) (M1)(A1)(ft)(G2)
Note: Award (M1) for \(17\), \(10\), \(27\) seen. Follow through from (a).[2 marks]
\(\frac{{40}}{{120}}{\text{ }}\left( {\frac{1}{3}{\text{, }}0.333{\text{, }}33.3\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{{34}}{{120}}{\text{ }}\left( {\frac{{17}}{{60}}{\text{, }}0.283{\text{, }}28.3\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{8}{{28}}{\text{ }}\left( {\frac{2}{7}{\text{, }}0.286{\text{, }}28.6\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
customer satisfaction is independent of café (A1)
Note: Accept “customer satisfaction is not associated with the café”.[1 mark]
\(2\) (A1)[1 mark]
\(0.754\) (G2)
Note: Award (G1)(G1)(AP) for \(0.75\) or for correct answer incorrectly rounded to 3 s.f. or more, (G0) for \(0.7\).[2 marks]
since \({\chi ^2}_{calc} < {\chi ^2}_{crit}5.991 accept (or Do not reject) H0 (R1)(A1)(ft)
Note: Follow through from their value in (e).
OR
Accept (or Do not reject) H0 as \(p\)-value \((0.686) > 0.05\) (R1)(A1)(ft)
Notes: Do not award (A1)(R0). Award the (R1) for comparison of appropriate values.[2 marks]
Question
Pam has collected data from a group of 400 IB Diploma students about the Mathematics course they studied and the language in which they were examined (English, Spanish or French). The summary of her data is given below.
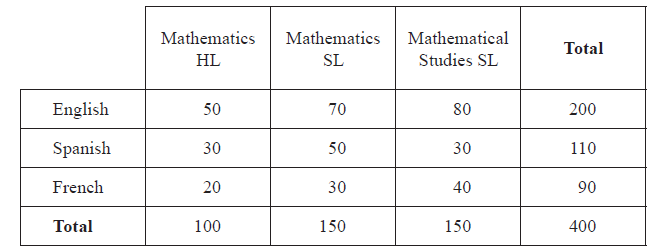
A student is chosen at random from the group. Find the probability that the student
(i) studied Mathematics HL;
(ii) was examined in French;
(iii) studied Mathematics HL and was examined in French;
(iv) did not study Mathematics SL and was not examined in English;
(v) studied Mathematical Studies SL given that the student was examined in Spanish.[8]
Pam believes that the Mathematics course a student chooses is independent of the language in which the student is examined.
Using your answers to parts (a) (i), (ii) and (iii) above, state whether there is any evidence for Pam’s belief. Give a reason for your answer.[2]
Pam decides to test her belief using a Chi-squared test at the \(5\% \) level of significance.
(i) State the null hypothesis for this test.
(ii) Show that the expected number of Mathematical Studies SL students who took the examination in Spanish is \(41.3\), correct to 3 significant figures.[3]
Write down
(i) the Chi-squared calculated value;
(ii) the number of degrees of freedom;
(iii) the Chi-squared critical value.[4]
State, giving a reason, whether there is sufficient evidence at the \(5\% \) level of significance that Pam’s belief is correct.[2]
Answer/Explanation
Markscheme
(i) \(\frac{{100}}{{400}}{\text{ }}\left( {\frac{1}{4}{\text{, }}0.25{\text{, }}25\% } \right)\) (A1)
(ii) \(\frac{{90}}{{400}}{\text{ }}\left( {\frac{9}{{40}}{\text{, }}0.225{\text{, }}22.5\% } \right)\) (A1)
(iii) \(\frac{{20}}{{400}}{\text{ }}\left( {\frac{1}{{20}}{\text{, }}0.05{\text{, }}5\% } \right)\) (A1)(A1)
Note: Award (A1) for numerator, (A1) for denominator.
(iv) \(\frac{{120}}{{400}}{\text{ }}\left( {\frac{3}{{10}}{\text{, }}0.3{\text{, }}30\% } \right)\) (A1)(A1)
Note: Award (A1) for numerator, (A1) for denominator.
(v) \(\frac{{30}}{{110}}{\text{ }}\left( {\frac{3}{{11}}{\text{, }}0.273{\text{, }}27.3\% } \right)\) (\(0.272727 \ldots \)) (A1)(A1)
Note: Award (A1) for numerator, (A1) for denominator. Accept \(0.27\), do not accept \(0.272\), do not accept \(0.3\).[8 marks]
\(\frac{1}{{20}} \ne \frac{1}{4} \times \frac{9}{{40}}\) (R1)(ft)
Note: The fractions must be used as part of the reason. Follow through from (a)(i), (a)(ii) and (a)(iii).
Pam is not correct. (A1)(ft)
Notes: Do not award (R0)(A1). Accept the events are not independent (dependent).[2 marks]
(i) The mathematics course and language of examination are independent. (A1)
Notes: Accept “There is no association between Mathematics course and language”. Do not accept “not related”, “not correlated”, “not influenced”.
(ii) \(\frac{{110}}{{400}} \times \frac{{150}}{{400}} \times 400{\text{ }}\left( { = \frac{{110 \times 150}}{{400}}} \right)\) (M1)
\( = 41.25\) (A1)
\( = 41.3\) (AG)
Note: \(41.25\) and \(41.3\) must be seen to award final (A1).[3 marks]
(i) \(7.67\) (\(7.67003 \ldots \)) (G2)
Note: Accept \(7.7\), do not accept \(8\) or \(7.6\). Award (G1) if formula with all nine terms seen but their answer is not one of those above.
(ii) \(4\) (G1)
(iii) \(9.488\) (A1)(ft)
Notes: Accept \(9.49\) or \(9.5\), do not accept \(9.4\) or \(9\). Follow through from their degrees of freedom.[4 marks]
\(7.67 < 9.488\) (R1)
OR
\(p = 0.104 \ldots , p > 0.05\) (R1)
Accept (Do not reject) \({H_0}\) (Pam’s belief is correct) (A1)(ft)
Notes: Follow through from part (d). Do not award (R0)(A1).[2 marks]
Question
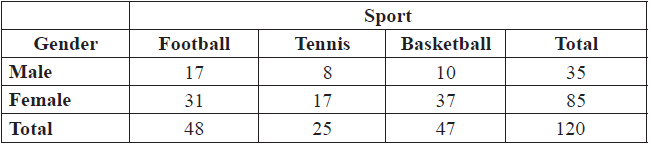
The seniors from Gulf High School are required to participate in exactly one after-school sport. Data were gathered from a sample of 120 students regarding their choice of sport. The following data were recorded.
A \({\chi ^2}\) test was carried out at the 5 % significance level to analyse the relationship between gender and choice of after-school sport.
Write down the null hypothesis, H0, for this test.[1]
Find the expected value of female footballers.[2]
Write down the number of degrees of freedom.[1]
Write down the critical value of \(\chi ^2\), at the 5 % level of significance.[1]
Use your graphic display calculator to determine the \(\chi _{calc}^2\) value.[2]
Determine whether H0 should be accepted. Justify your answer.[2]
One student is chosen at random from the 120 students.
Find the probability that this student
(i) is male;
(ii) plays tennis.[2]
Two students are chosen at random from the 120 students.
Find the probability that
(i) both play football;
(ii) neither play basketball.[5]
Answer/Explanation
Answer/Explanation
Markscheme
H0 : Gender and choice of afterschool sport are independent. (A1)
Note: Accept “not associated”, do not accept “not related”, “not correlated”, or “not linked”. Accept “the relation between gender and sport is independent”.[1 mark]
\(\frac{{85}}{{120}} \times \frac{{48}}{{120}} \times 120\left( {\frac{{85 \times 48}}{{120}}} \right)\) (M1)
Note: Award (M1) for correct expression.
= 34 (A1)(G2)[2 marks]
2 (A1)[1 mark]
5.99 (5.991) (A1)(ft)
Note: Follow through from part (c).[1 mark]
2.42 (2.42094…) (G2)[2 marks]
Since 2.42 < 5.99 therefore accept (do not reject) H0 (R1)(A1)(ft)
Note: The numerical values need not be seen, but must be consistent with their parts (d) and (e).
OR
p-value 0.298 > 0.05 therefore accept (do not reject) H0 (R1)(A1)
Note: p-value comparison may not be used as part of a follow through solution. Do not award (A1)(R0). Follow through from parts (c), (d) and (e).[2 marks]
(i) \(\frac{{35}}{{120}}\left( {\frac{7}{{24}},{\text{ }}0.292,{\text{ }}29.2\% } \right)\) (0.291666…) (A1)
(ii) \(\frac{{25}}{{120}}\left( {\frac{5}{{24}},{\text{ }}0.208,{\text{ }}20.8\% } \right)\) (0.208333…) (A1)[2 marks]
(i) \(\frac{{48}}{{120}} \times \frac{{47}}{{119}}\) (A1)(M1)
Note: Award (A1) for two correct fractions, (M1) for multiplying their two fractions.
\( = \frac{{94}}{{595}}(0.158,{\text{ }}15.8\% )\) (0.157983…) (A1)(G2)
(ii) \(\frac{{73}}{{120}} \times \frac{{72}}{{119}}\) (M1)
Note: Award (M1) for multiplying correct fractions. If sampling with replacement has been used in both parts (h)(i) and (h)(ii) do not penalise in part (h)(ii). Award a maximum of (M1)(A1)(ft).
\( = \frac{{219}}{{595}}(0.368,{\text{ }}36.8\% )\) (0.368067…) (A1)(G2) [5 marks]
Question
Leanne goes fishing at her favourite pond. The pond contains four different types of fish: bream, flathead, whiting and salmon. The fish are either undersized or normal. This information is shown in the table below.
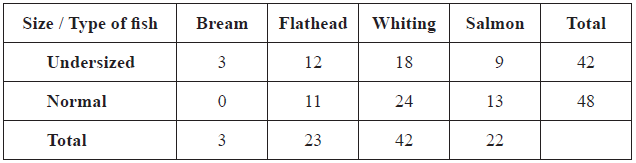
Write down the total number of fish in the pond.[1]
Leanne catches a fish.
Find the probability that she
(i) catches an undersized bream;
(ii) catches either a flathead or an undersized fish or both;
(iii) does not catch an undersized whiting;
(iv) catches a whiting given that the fish was normal.[7]
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Copy and complete the probability tree diagram below.
 [3]
[3]
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Calculate the probability that it is windy and Leanne catches a fish on a particular day.[2]
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Calculate the probability that Leanne catches a fish on a particular day.[3]
Use your answer to part (e) to calculate the probability that Leanne catches a fish on two consecutive days.[2]
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Given that Leanne catches a fish on a particular day, calculate the probability that the day was windy.[3]
Answer/Explanation
Markscheme
90 (A1)[1 mark]
(i) \(\frac{3}{{90}}(0.0\bar 3,{\text{ }}0.0333,{\text{ }}0.0333…,{\text{ }}3.\bar 3\% ,{\text{ }}3.33\% )\) (A1)(ft)
Note: For the denominator follow through from their answer in part (a).
(ii) \(\frac{{53}}{{90}}(0.5\bar 8,{\text{ }}0.588…,{\text{ }}0.589,{\text{ }}58.\bar 8\% ,{\text{ }}58.9\% )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for the numerator. (A1)(ft) for denominator. For the denominator follow through from their answer in part (a).
(iii) \(\frac{{72}}{{90}}{\text{(0.8, 80}}\%)\) (A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for the numerator, (their part (a) –18) (A1)(ft) for denominator. For the denominator follow through from their answer in part (a).
(iv) \(\frac{{24}}{{48}}(0.5,{\text{ 50}}\% )\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.[7 marks]
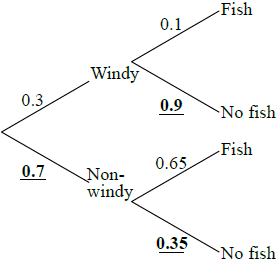 (A1)(A1)(A1)
(A1)(A1)(A1)
Notes: Award (A1) for each correct entry. Tree diagram must be seen for marks to be awarded.[3 marks]
\(0.3 \times 0.1 = 0.03\left( {\frac{3}{{100}}} \right)\) (M1)(A1)(G2)
Note: Award (M1) for correct product seen.[2 marks]
\(0.3 \times 0.1+ 0.7\times0.65\) (M1)(M1)
Notes: Award (M1) for \(0.7\times0.65\) (or 0.455) seen, (M1) for adding their 0.03. Follow through from their answers to parts (c) and (d).
\( = 0.485\left( {\frac{{485}}{{1000}},\frac{{97}}{{200}}} \right)\) (A1)(ft)(G2)
Note: Follow through from their tree diagram and their answer to part (d).[3 marks]
\(0.485 \times 0.485\) (M1)
\(0.235\left( {\frac{{9409}}{{40000}}{\text{, }}0.235225} \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (e).[2 marks]
\(\frac{{0.03}}{{0.485}}\) (M1)(A1)(ft)
Notes: Award (M1) for substituted conditional probability formula, (A1)(ft) for their (d) as numerator and their (e) as denominator.
\(0.0619\left( {\frac{{6}}{{97}}}\text{, 0.0618556…} \right) \) (A1)(ft)(G2)
Note: Follow through from their parts (d) and (e).[3 marks]
Question
A store recorded their sales of televisions during the 2010 football World Cup. They looked at the numbers of televisions bought by gender and the size of the television screens.
This information is shown in the table below; S represents the size of the television screen in inches.
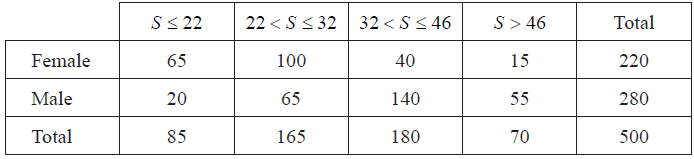
The store wants to use this information to predict the probability of selling these sizes of televisions for the 2014 football World Cup.
Use the table to find the probability that
(i) a television will be bought by a female;
(ii) a television with a screen size of 32 < S ≤ 46 will be bought;
(iii) a television with a screen size of 32 < S ≤ 46 will be bought by a female;
(iv) a television with a screen size greater than 46 inches will be bought, given that it is bought by a male.[6]
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Write down the null hypothesis.[1]
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Show that the expected frequency for females who bought a screen size of 32 < S ≤ 46, is 79, correct to the nearest integer.[2]
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Write down the number of degrees of freedom.[1]
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Write down the \({\chi ^2}\) calculated value.[2]
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Write down the critical value for this test.[1]
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Determine if the null hypothesis should be accepted. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
(i) \(\frac{{220}}{{500}}\left( {\frac{{11}}{{25}},{\text{ 0}}{\text{.44, 44}}\% } \right)\) (A1)(G1)
(ii) \(\frac{{180}}{{500}}\left( {\frac{{9}}{{25}},{\text{ 0}}{\text{.36, 36}}\% } \right)\) (A1)(G1)
(iii) \(\frac{{40}}{{500}}\left( {\frac{{2}}{{25}},{\text{ 0}}{\text{.08, 8}}\% } \right)\) (A1)(A1)(G2)
(iv) \(\frac{{55}}{{500}}\left( {\frac{{11}}{{56}},{\text{ 0}}{\text{.196, 19.6}}\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator. Award (A0)(A0) if answers are given as incorrect reduced fractions without working.[6 marks]
“The size of the television screen is independent of gender.” (A1)
Note: Accept “not associated”, do not accept “not correlated”.[1 mark]
\(\frac{{180}}{{500}} \times \frac{{220}}{{500}} \times 500\) OR \(\frac{{180 \times 220}}{{500}}\) (M1)
= 79.2 (A1)
= 79 (AG)
Note: Both the unrounded and the given answer must be seen for the final (A1) to be awarded.[2 marks]
3 (A1)[1 mark]
\(\chi _{calc}^2\) = 104(103.957…) (G2)
Note: Award (M1) if an attempt at using the formula is seen but incorrect answer obtained.[2 marks]
11.345 (A1)(ft)
Notes: Follow through from their degrees of freedom.[1 mark]
\(\chi _{calc}^2\) > \(\chi _{crit}^2\) OR p < 0.01 (R1)
Do not accept H0. (A1)(ft)
Note: Do not award (R0)(A1)(ft). Follow through from their parts (d), (e) and (f).[2 marks]
Question
100 students at IB College were asked whether they study Music (M), Chemistry (C), or Economics (E) with the following results.
10 study all three
15 study Music and Chemistry
17 study Music and Economics
12 study Chemistry and Economics
11 study Music only
6 study Chemistry only
Draw a Venn diagram to represent the information above.[4]
Write down the number of students who study Music but not Economics.[1]
There are 22 Economics students in total.
(i) Calculate the number of students who study Economics only.
(ii) Find the number of students who study none of these three subjects.[4]
A student is chosen at random from the 100 that were asked above.
Find the probability that this student
(i) studies Economics;
(ii) studies Music and Chemistry but not Economics;
(iii) does not study either Music or Economics;
(iv) does not study Music given that the student does not study Economics.[7]
Answer/Explanation
Markscheme
(A1) for rectangle and three labelled circles (U need not be seen)
(A1) for 10 in the correct region
(A1) for 2, 7 and 5 in the correct regions
(A1) for 6 and 11 in the correct regions (A4)
16 (A1)(ft)
Note: Follow through from their Venn diagram.
(i) \(10 + 7 + 2\) (M1)
Note: Award (M1) for summing their 10, 7 and 2.
\(22 – 19\)
\(= 3\) (A1)(ft)(G2)
Note: Follow through from their diagram. Award (M1)(A1)(ft) for answers consistent with their diagram irrespective of whether working seen. Award a maximum of (M1)(A0) for a negative answer.
(ii) \(22 + 11+ 5 + 6\) (M1)
Note: Award (M1) for summing 22, and their 11, 5 and 6.
\(100 – 44\)
\(= 56\) (A1)(ft)(G2)
Note: Follow through from their diagram. Award (M1)(A1)(ft) for answers consistent with their diagram and the use of 22 irrespective of whether working seen. If negative values are used or implied award (M0)(A0).
(i) \(\frac{{22}}{{100}}\left( {\frac{{11}}{{50}},0.22,22\% } \right)\) (A1)(G1)
(ii) \(\frac{{5}}{{100}}\left( {\frac{{1}}{{20}},0.05,5\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for their 5 in numerator, (A1) for denominator.
Follow through from their diagram.
(iii) \(\frac{{62}}{{100}}\left( {\frac{{31}}{{50}},0.62,62\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for \(100 – (22 + 11 + {\text{their }}5)\), (A1) for denominator.
Follow through from their diagram.
(iv) \(\frac{{62}}{{78}}\left( {\frac{{31}}{{39}},0.795,79.5\% } \right)\) (0.794871…) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow
through from part (d)(iii) for numerator.
Question
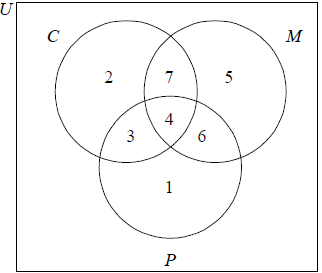
Forty families were surveyed about the places they went to on the weekend. The places were the circus (C), the museum (M) and the park (P).
16 families went to the circus
22 families went to the museum
14 families went to the park
4 families went to all three places
7 families went to both the circus and the museum, but not the park
3 families went to both the circus and the park, but not the museum
1 family went to the park only
Draw a Venn diagram to represent the given information using sets labelled C, M and P. Complete the diagram to include the number of families represented in each region.[4]
Find the number of families who
(i) went to the circus only;
(ii) went to the museum and the park but not the circus;
(iii) did not go to any of the three places on the weekend.[4]
A family is chosen at random from the group of 40 families. Find the probability that the family went to
(i) the circus;
(ii) two or more places;
(iii) the park or the circus, but not the museum;
(iv) the museum, given that they also went to the circus.[8]
Two families are chosen at random from the group of 40 families.
Find the probability that both families went to the circus.[3]
Answer/Explanation
Markscheme
 (A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)
Award (A1) for 3 intersecting circles and rectangle, (A1) for 1, 3, 4 and 7, (A1) for 2, (A1) for 6 and 5.
(i) 2 (A1)(ft)
(ii) 6 (A1)(ft)
(iii) 40 − (1 + 6 + 2 + 3 + 4 + 7 + 5) (M1)
Note: Award (M1) for subtracting all their values from 40.
= 12 (A1)(ft)(G2)
Note: Follow through from their Venn diagram for parts (i), (ii) and (iii).
(i) \(\frac{{16}}{{40}}\left( {\frac{2}{5},0.4,40\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator. Answer must be less than 1 otherwise award (A0)(A0). Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
(ii) \(\frac{{20}}{{40}}\left( {\frac{1}{2},0.5,50\% } \right)\) (A1)(ft) (A1) (G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram. Answer must be less than 1 otherwise award (A0)(A0). Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
(iii) \(\frac{6}{{40}}\left( {\frac{3}{{20}},0.15,15\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram. Answer must be less than 1 otherwise award (A0)(A0). Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
(iv) \(\frac{{11}}{{16}}\left( {0.6875,68.75\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram. Answer must be less than 1 otherwise award (A0)(A0). Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
\(\frac{{16}}{{40}} \times \frac{{15}}{{39}}\) (A1)(A1)(ft)
Note: Award (A1) for multiplication of their probabilities, (A1)(ft) for their correct probabilities.
\(\frac{{240}}{{1560}}\left( {\frac{2}{{13}},0.153846…,15.4\% } \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (c)(i). Answer must be less than 1 otherwise award at most (A1)(A1)(A0)(ft).
Question
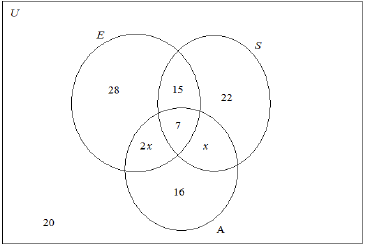
A group of \(120\) women in the USA were asked whether they had visited the continents of Europe (\(E\)) or South America (\(S\)) or Asia (\(A\)).
\(7\) had visited all three continents
\(28\) had visited Europe only
\(22\) had visited South America only
\(16\) had visited Asia only
\(15\) had visited Europe and South America but had not visited Asia
\(x\) had visited South America and Asia but had not visited Europe
\(2x\) had visited Europe and Asia but had not visited South America
\(20\) had not visited any of these continents
Draw a Venn diagram, using sets labelled \(E\), \(S\) and \(A\), to show this information.[5]
Calculate the value of \(x\).[2]
Explain, in words, the meaning of \((E \cup S) \cap A’\).[2]
Write down \(n\left( {(E \cup S \cup A)’} \right)\).[1]
Find the probability that a woman selected at random from the group had visited Europe.[2]
Find the probability that a woman selected at random from the group had visited Europe, given that she had visited Asia.
Two women from the group are selected at random.
Find the probability that both women selected had visited South America.[3]
Answer/Explanation
Markscheme
 (A1)(A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)(A1)
Notes: Award (A1) for rectangle and three labelled intersecting circles.
Award (A1) for \(7\) in correct place.
Award (A1) for \(28\), \(22\) and \(16\) in the correct places.
Award (A1) for \(15\), \(x\) and \(2x\) in the correct places.
Award (A1) for \(20\) in the correct place.
Accept \(4\) and \(8\) instead of \(x\) and \(2x\).
Do not penalize if \(U\) is omitted from the diagram.[5 marks]
\(3x = 120 – (20 + 28 + 15 + 22 + 7 + 16)\) (M1)
Note: Award (M1) for setting up a correct equation involving \(x\), the \(120\) and values from their diagram.
\(x = 4\) (A1)(ft)(G2)
Note: Follow through from part (a). For the follow through to be awarded \(x\) must be a positive integer.[2 marks]
(Women who had visited) Europe or South America and (but had) not (visited) Asia (A1)(A1)
Notes: Award (A1) for “(visited) Europe or South America” (or both).
Award (A1) for “and (but) had not visited Asia”.
\(E\)(urope) union \(S\)(outh America) intersected with not \(A\)(sia) earns no marks, (A0).[2 marks]
\(20\) (A1)
Note: Award (A0) for the embedded answer of \(n(20)\).[1 mark]
\(\frac{{58}}{{120}}{\text{ }}\left( {\frac{{29}}{{60}},{\text{ 0.483, 48.3% }}} \right){\text{ (0.48333}} \ldots {\text{)}}\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, follow through from their value of \(x\), or their diagram, (A1) for denominator.[2 marks]
\(\frac{{15}}{{35}}{\text{ }}\left( {\frac{3}{7},{\text{ 0.429, 42.9% }}} \right){\text{ (0.428571}} \ldots {\text{)}}\) (A1)(ft)(A1)(ft)(G2)
Note: Award (A1)(ft) for numerator, (A1)(ft) for denominator, follow through from their value of \(x\) or their diagram. [2 marks]
\(\frac{{48}}{{120}} \times \frac{{47}}{{119}}\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for two correct fractions, follow through from their denominator in part (e), follow through the numerator from their answer to part (b) or from their diagram, (M1) for multiplication of their two fractions.
\( = \frac{{2256}}{{14\,280}}\left( {\frac{{94}}{{595}},{\text{ 0.158, 15,8% }}} \right){\text{ (0.157983}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Award (A1)(M1)(A1) for correct fractions, correctly multiplied together with an answer of \(0.16\).
Award (A0)(M1)(A0) for \(\frac{{48}}{{120}} \times \frac{{48}}{{120}} = 0.16\).
Award (G1) for an answer of \(0.16\) with no working seen.[3 marks]
Question
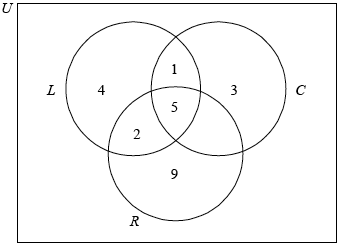
A group of tourists went on safari to a game reserve. The game warden wanted to know how many of the tourists saw Leopard (\(L\)), Cheetah (\(C\)) or Rhino (\(R\)). The results are given as follows.
5 of the tourists saw all three
7 saw Leopard and Rhino
1 saw Cheetah and Leopard but not Rhino
4 saw Leopard only
3 saw Cheetah only
9 saw Rhino only
Draw a Venn diagram to show this information.[4]
There were 25 tourists in the group and every tourist saw at least one of the three types of animal.
Find the number of tourists that saw Cheetah and Rhino but not Leopard.[2]
There were 25 tourists in the group and every tourist saw at least one of the three types of animal.
Calculate the probability that a tourist chosen at random from the group
(i) saw Leopard;
(ii) saw only one of the three types of animal;
(iii) saw only Leopard, given that he saw only one of the three types of animal.[6]
There were 25 tourists in the group and every tourist saw at least one of the three types of animal.
If a tourist chosen at random from the group saw Leopard, find the probability that he also saw Cheetah.[2]
Answer/Explanation
Markscheme
 (A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)
Note: Award (A1) for rectangle and three labelled intersecting circles (the rectangle need not be labelled), (A1) for 5, (A1) for 2 and 1, (A1) for 4, 3 and 9.[4 marks]
\(25 – (5 + 2 + 1 + 4 + 3 + 9)\) (M1)
Notes: Award (M1) for their \(5 + 2 + 1 + 4 + 3 + 9\) seen even if total is greater than \(25\).
Do not award (A1)(ft) if their total is greater than \(25\).
\( = 1\) (A1)(ft)(G2)[2 marks]
(i) \(\frac{{12}}{{25}}{\text{ }}(0.48,{\text{ }}48\% )\) (A1)(ft)(A1)(G2)
Notes: Award (A1)(ft) for numerator, (A1) for denominator.
Follow through from Venn diagram.
(ii) \(\frac{{16}}{{25}}{\text{ }}(0.64,{\text{ }}64\% )\) (A1)(A1)(G2)
Notes: Award (A1) for numerator, (A1) for denominator.
There is no follow through; all information is given.
(iii) \(\frac{4}{{16}}{\text{ }}(0.25,{\text{ }}25\% )\)) (A1)(A1)(ft)(G2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator.
Follow through from part (c)(ii) only.[6 marks]
\(\frac{6}{{12}}{\text{ }}(0.5,{\text{ }}50\% )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator.
Follow through from Venn diagram.[2 marks]
Question
Tomek is attending a conference in Singapore. He has both trousers and shorts to wear. He also has the choice of wearing a tie or not.
The probability Tomek wears trousers is \(0.3\). If he wears trousers, the probability that he wears a tie is \(0.8\).
If Tomek wears shorts, the probability that he wears a tie is \(0.15\).
The following tree diagram shows the probabilities for Tomek’s clothing options at the conference.
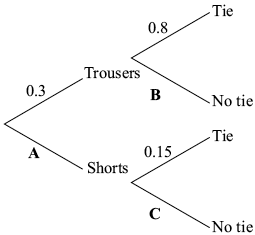
Find the value of
(i) \({\text{A}}\);
(ii) \({\text{B}}\);
(iii) \({\text{C}}\).[3]
Calculate the probability that Tomek wears
(i) shorts and no tie;
(ii) no tie;
(iii) shorts given that he is not wearing a tie.[8]
The conference lasts for two days.
Calculate the probability that Tomek wears trousers on both days.[2]
The conference lasts for two days.
Calculate the probability that Tomek wears trousers on one of the days, and shorts on the other day.[3]
Answer/Explanation
Markscheme
(i) \(0.7 \left( {\frac{{70}}{{100}},{\text{ }}\frac{7}{{10}},{\text{ 70% }}} \right)\) (A1)
(ii) \(0.2 \left( {\frac{{20}}{{100}},{\text{ }}\frac{2}{{10}},{\text{ }}\frac{1}{5},{\text{ 20% }}} \right)\) (A1)
(iii) \(0.85 \left( {\frac{{85}}{{100}},{\text{ }}\frac{{17}}{{20}},{\text{ 85% }}} \right)\) (A1)[3 marks]
(i) \(0.7 \times 0.85\) (M1)
Note: Award (M1) for multiplying their values from parts (a)(i) and (a)(iii).
\( = 0.595{\text{ }}\left( {\frac{{119}}{{200}},{\text{ 59.5% }}} \right)\) (A1)(ft)(G1)
Note: Follow through from part (a).
(ii) \(0.3 \times 0.2 + 0.7 \times 0.85\) (M1)(M1)
Note: Award (M1) for their two products, (M1) for adding their two products.
\( = 0.655{\text{ }}\left( {\frac{{131}}{{200}},{\text{ 65.5% }}} \right)\) (A1)(ft)(G2)
Note: Follow through from part (a).
(iii) \(\frac{{0.595}}{{0.655}}\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for correct numerator, (A1)(ft) for correct denominator. Follow through from parts (b)(i) and (ii).
\( = 0.908{\text{ }}\left( {{\text{0.90839}} \ldots ,{\text{ }}\frac{{119}}{{131}},{\text{ 90,8% }}} \right)\) (A1)(ft)(G2)[8 marks]
\(0.3 \times 0.3\) (M1)
\( = 0.09 \left( {\frac{9}{{100}}, 9\%} \right)\) (A1)(G2)[2 marks]
\(0.3 \times 0.7\) (M1)
\(0.3 \times 0.7 \times 2\) OR \((0.3 \times 0.7) + (0.7 \times 0.3)\) (M1)
Note: Award (M1) for their correct product seen, (M1) for multiplying their product by 2 or for adding their products twice.
\( = 0.42 \left( {\frac{{42}}{{100}}, \frac{{21}}{{50}}, 42\%} \right)\) (A1)(ft)(G2)
Note: Follow through from part (a)(i).[3 marks]
Question
Mike, the laboratory mouse, is placed at the starting point, S, of a maze. Some paths in the maze lead to Trap A, some to Trap B, and others to escape doors. Some paths have one and some have two sections. If his path forks, Mike randomly chooses a path forward.
The following tree diagram represents the maze, showing all possible paths, and the probability that Mike chooses a certain section of a path through the maze.
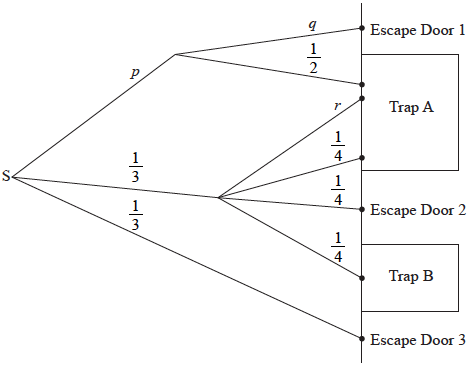
Write down the value of
(i) \(p\) ;
(ii) \(q\) ;
(iii) \(r\).[3]
(i) Find the probability that Mike reaches Trap B.
(ii) Find the probability that Mike reaches Trap A.
(iii) Find the probability that Mike escapes from the maze.[7]
Sonya, a lab assistant, counts the number of paths that lead to traps or escape doors. She believes that the probability that Mike will be trapped is greater than the probability that he will escape.
State whether Sonya is correct. Give a mathematical justification for your conclusion.[2]
During the first trial Mike escapes.
Given that Mike escaped, find the probability that he went directly from S to Escape Door 3.[3]
Answer/Explanation
Markscheme
(i) \(\frac{1}{3}\;\;\;(0.333333…,{\text{ }}33.3333…\% )\) (A1)
(ii) \(\frac{1}{2}\;\;\;(0.5,{\text{ }}50\% )\) (A1)
(iii) \(\frac{1}{4}\;\;\;(0.25,{\text{ }}25\% )\) (A1)
(i) \(\frac{1}{3} \times \frac{1}{4}\) (M1)
\( = \frac{1}{{12}}\;\;\;({\text{0.0833333…, 8.33333…% )}}\) (A1)(G2)
(ii) \(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3} \times \frac{1}{4}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their three correct products seen, (M1) for addition of their products.
\( = \frac{1}{3}\;\;\;(0.333333…,{\text{ }}33.3333…\% )\) (A1)(ft)(G2)
Note: Follow through from their parts (a)(i) and (a)(iii).
(iii) \(1 – \frac{1}{{12}} – \frac{1}{3}\) (M1)
Note: Follow through from parts (b)(i) and (b)(ii).
OR
\(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3}\) (M1)
Note: Follow through from parts (a)(i) and (a)(ii).
\( = \frac{7}{{12}}\;\;\;(0.583333…,{\text{ }}58.3333…\% )\) (A1)(ft)(G2)
Sonya is not correct. (A1)(ft)
The probability that Mike escapes is \(\frac{7}{{12}}\), which is
greater than \(\frac{5}{{12}}{\text{ }}\left( {{\text{or greater than }}\frac{1}{2}} \right)\). (R1)(ft)
Notes: Do not award (A1)(R0).
Follow through from their answers to part (b).
\(\frac{{\frac{1}{3}}}{{\frac{7}{{12}}}}\) (A1)(A1)(ft)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
\( = \frac{4}{7}\;\;\;\left( {\frac{{12}}{{21}},{\text{ 0.571428…, 57.1428…% }}} \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (b)(iii).
Question
A group of 100 customers in a restaurant are asked which fruits they like from a choice of mangoes, bananas and kiwi fruits. The results are as follows.
15 like all three fruits
22 like mangoes and bananas
33 like mangoes and kiwi fruits
27 like bananas and kiwi fruits
8 like none of these three fruits
\(x\) like only mangoes
Copy the following Venn diagram and correctly insert all values from the above information.
 [3]
[3]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Complete your Venn diagram from part (a) with this additional information in terms of \(x\).[2]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Find the value of \(x\).[2]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Write down the number of customers who like
(i) mangoes;
(ii) mangoes or bananas.[2]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
A customer is chosen at random from the 100 customers. Find the probability that this customer
(i) likes none of the three fruits;
(ii) likes only two of the fruits;
(iii) likes all three fruits given that the customer likes mangoes and bananas.[4]
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Two customers are chosen at random from the 100 customers. Find the probability that the two customers like none of the three fruits.[3]
Answer/Explanation
Markscheme
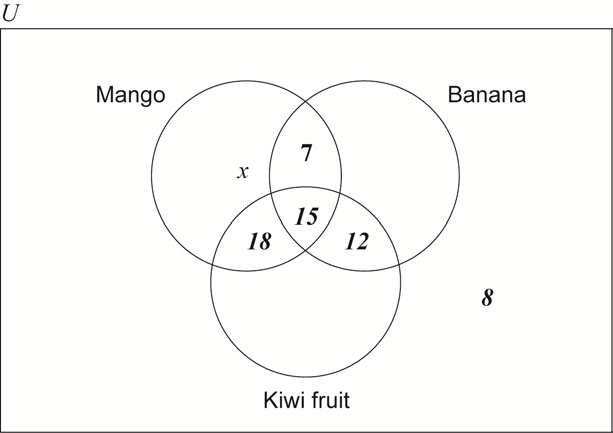 (A1)(A1)(A1)
(A1)(A1)(A1)
Notes: Award (A1) for 15 in the correct place.
Award (A1) for 7, 18 and 12 seen in the correct places.
Award (A1) for 8 in the correct place.
Award at most (A0)(A1)(A1) if diagram is missing the rectangle.
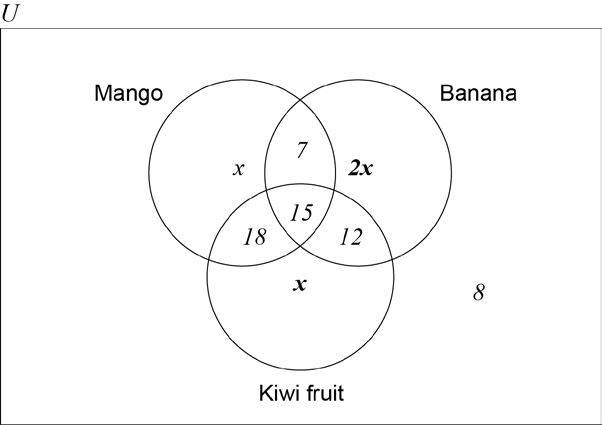 (A1)(A1)
(A1)(A1)
Notes: Award (A1) for \(x\) seen in the correct places.
Award (A1) for \(2x\) seen in the correct place.
Award (A0)(A1)(ft) if \(x\) and \(2x\) are replaced by 10 and 20 respectively.
\(2x + x + x + 15 + 8 + 7 + 18 + 12 = 100\;\;\;(4x + 60 = 100{\text{ or equivalent)}}\) (M1)
Note: Award (M1) for equating the sum of the elements of their Venn diagram to \(100\). Equating to \(100\) may be implied.
\((x = ){\text{ }}10\) (A1)(ft)(G2)
Note: Follow through from their Venn diagram. The answer must be a positive integer.
(i) \(50\) (A1)(ft)
(ii) \(82\) (A1)(ft)
Note: Follow through from their answer to part (c) and their Venn diagram.
Award (A0)(ft)(A1)(ft) if answer is \(\frac{{50}}{{100}}\) and \(\frac{{82}}{{100}}\).
(i) \(\frac{8}{{100}}\;\;\;\left( {\frac{2}{{25}};{\text{ }}0.08;{\text{ }}8\% } \right)\) (A1)
Note: Correct answer only. There is no follow through.
(ii) \(\frac{{37}}{{100}}\;\;\;(0.37,{\text{ }}37\% )\) (A1)(ft)
Note: Follow through from their Venn diagram.
(iii) \(\frac{{15}}{{22}}\;\;\;(0.681;{\text{ }}0.682;{\text{ }}68.2\% )\;\;\;(0.681818 \ldots )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator, follow through from their Venn diagram. Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
\(\frac{8}{{100}} \times \frac{7}{{99}}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for correct fractions, follow through from their answer to part (e)(i), (M1) for multiplying their fractions.
\( = \frac{{56}}{{9900}}\;\;\;\left( {\frac{{14}}{{2477}},{\text{ }}0.00565656 \ldots ,{\text{ }}0.00566,{\text{ }}0.0056,{\text{ }}0.566\% } \right)\) (A1)(ft)(G2)
Question
A group of 66 people went on holiday to Hawaii. During their stay, three trips were arranged: a boat trip (\(B\)), a coach trip (\(C\)) and a helicopter trip (\(H\)).
From this group of people:
| 3 | went on all three trips; |
| 16 | went on the coach trip only; |
| 13 | went on the boat trip only; |
| 5 | went on the helicopter trip only; |
| x | went on the coach trip and the helicopter trip but not the boat trip; |
| 2x | went on the boat trip and the helicopter trip but not the coach trip; |
| 4x | went on the boat trip and the coach trip but not the helicopter trip; |
| 8 | did not go on any of the trips. |
One person in the group is selected at random.
Draw a Venn diagram to represent the given information, using sets labelled \(B\), \(C\) and \(H\).[5]
Show that \(x = 3\).[2]
Write down the value of \(n(B \cap C)\).[1]
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.[4]
Answer/Explanation
Markscheme
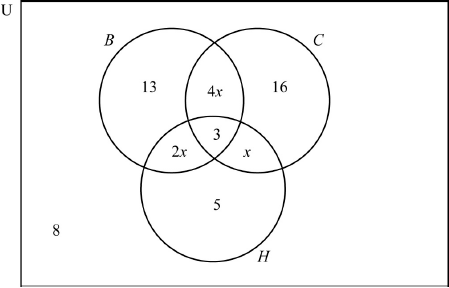 (A5)
(A5)
Notes: Award (A1) for rectangle and three labelled intersecting circles (U need not be seen),
(A1) for 3 in the correct region,
(A1) for 8 in the correct region,
(A1) for 5, 13 and 16 in the correct regions,
(A1) for \(x\), \(2x\) and \(4x\) in the correct regions.[5 marks]
\(8 + 13 + 16 + 3 + 5 + x + 2x + 4x = 66\) (M1)
Note: Award (M1) for either a completely correct equation or adding all the terms from their diagram in part (a) and equating to 66.
Award (M0)(A0) if their equation has no \(x\).
\(7x = 66 – 45\) OR \(7x + 45 = 66\) (A1)
Note: Award (A1) for adding their like terms correctly, but only when the solution to their equation is equal to 3 and is consistent with their original equation.
\(x = 3\) (AG)
Note: The conclusion \(x = 3\) must be seen for the (A1) to be awarded.[2 marks]
15 (A1)(ft)
Note: Follow through from part (a). The answer must be an integer.[1 mark]
(i) \(\frac{{42}}{{66}}{\text{ }}\left( {\frac{7}{{11}},{\text{ }}0.636,{\text{ }}63.6\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram.
(ii) \(\frac{3}{9}{\text{ }}\left( {\frac{1}{3},{\text{ }}0.333,{\text{ }}33.3\% } \right)\) (A1)(A1)(ft)(G2)
Note: Award (A1) for numerator, (A1)(ft) for denominator. Follow through from their Venn diagram.[4 marks]
Question
A company performs an experiment on the efficiency of a liquid that is used to detect a nut allergy.
A group of 60 people took part in the experiment. In this group 26 are allergic to nuts. One person from the group is chosen at random.
A second person is chosen from the group.
When the liquid is added to a person’s blood sample, it is expected to turn blue if the person is allergic to nuts and to turn red if the person is not allergic to nuts.
The company claims that the probability that the test result is correct is 98% for people who are allergic to nuts and 95% for people who are not allergic to nuts.
It is known that 6 in every 1000 adults are allergic to nuts.
This information can be represented in a tree diagram.
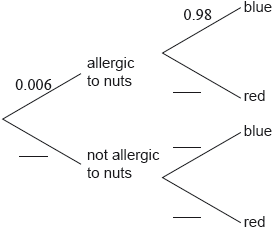
An adult, who was not part of the original group of 60, is chosen at random and tested using this liquid.
The liquid is used in an office to identify employees who might be allergic to nuts. The liquid turned blue for 38 employees.
Find the probability that this person is not allergic to nuts.[2]
Find the probability that both people chosen are not allergic to nuts.[2]
Copy and complete the tree diagram.[3]
Find the probability that this adult is allergic to nuts and the liquid turns blue.[2]
Find the probability that the liquid turns blue.[3]
Find the probability that the tested adult is allergic to nuts given that the liquid turned blue.[3]
Estimate the number of employees, from this 38, who are allergic to nuts.[2]
Answer/Explanation
Markscheme
\(\frac{{34}}{{60}}{\text{ }}\left( {\frac{{17}}{{30}},{\text{ }}0.567,{\text{ }}0.566666 \ldots ,{\text{ }}56.7\% } \right)\) (A1)(A1
Note: Award (A1) for correct numerator, (A1) for correct denominator.[2 marks]
\(\frac{{34}}{{60}} \times \frac{{33}}{{59}}\) (M1)
Note: Award (M1) for their correct product.
\( = 0.317{\text{ }}\left( {\frac{{187}}{{590}},{\text{ }}0.316949 \ldots ,{\text{ }}31.7\% } \right)\) (A1)(ft)(G2)
Note: Follow through from part (a).[2 marks]
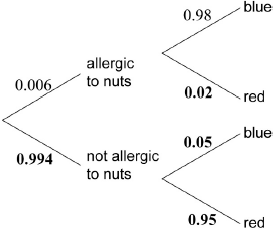 (A1)(A1)(A1)
(A1)(A1)(A1)
Note: Award (A1) for each correct pair of branches.[3 marks]
\(0.006 \times 0.98\) (M1)
Note: Award (M1) for multiplying 0.006 by 0.98.
\( = 0.00588{\text{ }}\left( {\frac{{147}}{{25000}},{\text{ }}0.588\% } \right)\) (A1)(G2)[2 marks]
\(0.006 \times 0.98 + 0.994 \times 0.05{\text{ }}(0.00588 + 0.994 \times 0.05)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their two correct products, (M1) for adding two products.
\( = 0.0556{\text{ }}\left( {0.05558,{\text{ }}5.56\% ,{\text{ }}\frac{{2779}}{{50000}}} \right)\) (A1)(ft)(G3)
Note: Follow through from parts (c) and (d).[3 marks]
\(\frac{{0.006 \times 0.98}}{{0.05558}}\) (M1)(M1)
Note: Award (M1) for their correct numerator, (M1) for their correct denominator.
\( = 0.106{\text{ }}\left( {0.105793 \ldots ,{\text{ }}10.6\% ,{\text{ }}\frac{{42}}{{397}}} \right)\) (A1)(ft)(G3)
Note: Follow through from parts (d) and (e).[3 marks]
\(0.105793 \ldots \times 38\) (M1)
Note: Award (M1) for multiplying 38 by their answer to part (f).
\( = 4.02{\text{ }}(4.02015 \ldots )\) (A1)(ft)(G2)
Notes: Follow through from part (f). Use of 3 sf result from part (f) results in an answer of 4.03 (4.028).[2 marks]
Question
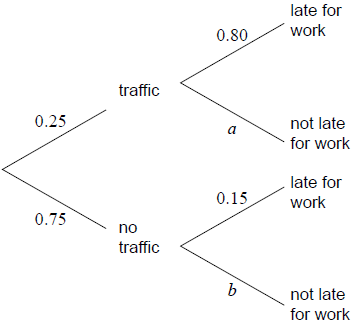
In a company it is found that 25 % of the employees encountered traffic on their way to work. From those who encountered traffic the probability of being late for work is 80 %.
From those who did not encounter traffic, the probability of being late for work is 15 %.
The tree diagram illustrates the information.
The company investigates the different means of transport used by their employees in the past year to travel to work. It was found that the three most common means of transport used to travel to work were public transportation (P ), car (C ) and bicycle (B ).
The company finds that 20 employees travelled by car, 28 travelled by bicycle and 19 travelled by public transportation in the last year.
Some of the information is shown in the Venn diagram.
There are 54 employees in the company.
Write down the value of a.[1]
Write down the value of b.[1]
Use the tree diagram to find the probability that an employee encountered traffic and was late for work.
Use the tree diagram to find the probability that an employee was late for work.[3]
Use the tree diagram to find the probability that an employee encountered traffic given that they were late for work.[3]
Find the value of x.[1]
Find the value of y.[1]
Find the number of employees who, in the last year, did not travel to work by car, bicycle or public transportation.[2]
Find \(n\left( {\left( {C \cup B} \right) \cap P’} \right)\).[2]
Answer/Explanation
Markscheme
a = 0.2 (A1)[1 mark]
b = 0.85 (A1)[1 mark]
0.25 × 0.8 (M1)
Note: Award (M1) for a correct product.
\( = 0.2\,\,\,\left( {\,\frac{1}{5},\,\,\,20\% } \right)\) (A1)(G2)[2 marks]
0.25 × 0.8 + 0.75 × 0.15 (A1)(ft)(M1)
Note: Award (A1)(ft) for their (0.25 × 0.8) and (0.75 × 0.15), (M1) for adding two products.
\( = 0.313\,\,\,\left( {0.3125,\,\,\,\frac{5}{{16}},\,\,\,31.3\% } \right)\) (A1)(ft)(G3)
Note: Award the final (A1)(ft) only if answer does not exceed 1. Follow through from part (b)(i).[3 marks]
\(\frac{{0.25 \times 0.8}}{{0.25 \times 0.8 + 0.75 \times 0.15}}\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for a correct numerator (their part (b)(i)), (A1)(ft) for a correct denominator (their part (b)(ii)). Follow through from parts (b)(i) and (b)(ii).
\( = 0.64\,\,\,\left( {\frac{{16}}{{25}},\,\,64{\text{% }}} \right)\) (A1)(ft)(G3)
Note: Award final (A1)(ft) only if answer does not exceed 1.[3 marks]
(x =) 3 (A1)[1 Mark]
(y =) 10 (A1)(ft)
Note: Following through from part (c)(i) but only if their x is less than or equal to 13.[1 Mark]
54 − (10 + 3 + 4 + 2 + 6 + 8 + 13) (M1)
Note: Award (M1) for subtracting their correct sum from 54. Follow through from their part (c).
= 8 (A1)(ft)(G2)
Note: Award (A1)(ft) only if their sum does not exceed 54. Follow through from their part (c).[2 marks]
6 + 8 + 13 (M1)
Note: Award (M1) for summing 6, 8 and 13.
27 (A1)(G2)[2 marks]
Question
\(50\) students at Rambling High School were asked how they travelled to school yesterday. All of the students travelled by bus, by car or walked.
\(12\) students travelled by car only
\(7\) students travelled by bus only
\(5\) students travelled by car and walked, but did not use a bus
\(10\) students travelled by bus and walked, but did not use a car
\(3\) students used all three forms of travel.
Represent this information on a Venn Diagram.[4]
There were \(28\) students who used a bus to travel to school. Calculate the number of students
(i) who travelled by car and by bus but did not walk;
(ii) who travelled by car.[4]
Tomoko used a bus to travel to school yesterday.
Find the probability that she also walked.[2]
Two students are chosen at random from all \(50\) students.
Find the probability that
(i) both students walked;
(ii) only one of the students walked.[7]
Answer/Explanation
Markscheme
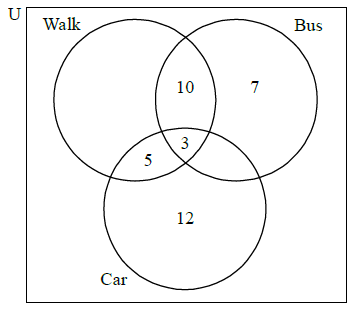 (A4)
(A4)
Note: Award (A1) for rectangle and three labelled intersecting circles, (A1) for \(3\), (A1) for \(5\) and \(10\), (A1) for \(7\) and \(12\).
(i) \(28 – (10 + 3 + 7) = 8\) (M1)(A1)(ft)(G2)
Note: Follow through from their Venn diagram.
(ii) \(5 + 3 + 8 + 12 = 28\) (M1)(A1)(ft)(G2)
Note: Follow through from part (b)(i) and their Venn diagram.
\({\text{P(}}\left. {{\text{walk}}} \right|{\text{bus}}) = \frac{{13}}{{28}}\) \((0.464{\text{, }}46.4\% )\) (\(0.464285 \ldots \)) (A1)(A1)(ft)(G2)
Note: Award (A1)(ft) for the numerator, (A1) for denominator.
(i) \(\frac{{23}}{{50}} \times \frac{{22}}{{49}}\) (A1)(M1)(M1)
Note: Award (A1) for \(23\) seen, (M1) for non replacement, (M1) for multiplying their fractions.
\( = \frac{{506}}{{2450}}\) \((0.207{\text{, }}20.7\% )\) (\(0.206530 \ldots \)) (A1)(G3)
(ii) \(\frac{{23}}{{50}} \times \frac{{27}}{{49}} + \frac{{27}}{{50}} \times \frac{{23}}{{49}}\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for two products, (M1) for adding two products. Do not penalise in (ii) for consistent use of with replacement.
\( = \frac{{1242}}{{2450}}\) \((0.507{\text{, }}50.7\% )\) (\(0.509638 \ldots \)) (A1)(ft)(G2)
