Question
The figure below shows the lengths in centimetres of fish found in the net of a small trawler.
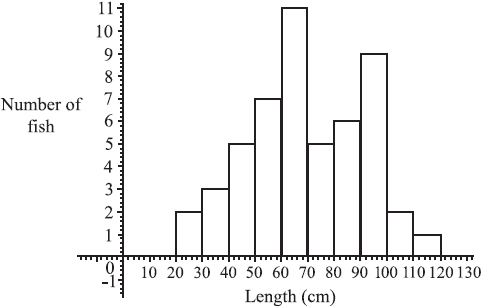
Find the total number of fish in the net.[2]
Find (i) the modal length interval,
(ii) the interval containing the median length,
(iii) an estimate of the mean length.[5]
(i) Write down an estimate for the standard deviation of the lengths.
(ii) How many fish (if any) have length greater than three standard deviations above the mean?[3]
The fishing company must pay a fine if more than 10% of the catch have lengths less than 40cm.
Do a calculation to decide whether the company is fined.[2]
A sample of 15 of the fish was weighed. The weight, W was plotted against length, L as shown below.
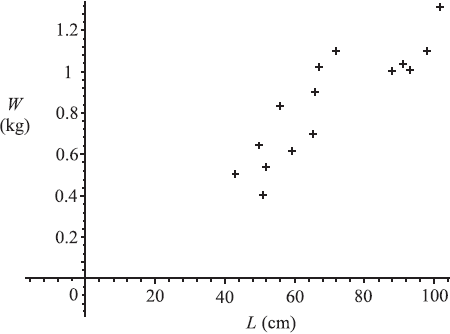
Exactly two of the following statements about the plot could be correct. Identify the two correct statements.
Note: You do not need to enter data in a GDC or to calculate r exactly.
(i) The value of r, the correlation coefficient, is approximately 0.871.
(ii) There is an exact linear relation between W and L.
(iii) The line of regression of W on L has equation W = 0.012L + 0.008 .
(iv) There is negative correlation between the length and weight.
(v) The value of r, the correlation coefficient, is approximately 0.998.
(vi) The line of regression of W on L has equation W = 63.5L + 16.5.[2]
Answer/Explanation
Markscheme
Total = 2 + 3 + 5 + 7 + 11 + 5 + 6 + 9 + 2 + 1 (M1)
(M1) is for a sum of frequencies.
= 51 (A1)(G2)[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) modal interval is 60 – 70
Award (A0) for 65 (A1)
(ii) median is length of fish no. 26, (M1)(A1)
also 60 – 70 (G2)
Can award (A1)(ft) or (G2)(ft) for 65 if (A0) was awarded for 65 in part (i).
(iii) mean is \(\frac{{2 \times 25 + 3 \times 35 + 5 \times 45 + 7 \times 55 + …}}{{51}}\) (M1)
(UP) = 69.5 cm (3sf) (A1)(ft)(G1)
Note: (M1) is for a sum of (frequencies multiplied by midpoint values) divided by candidate’s answer from part (a). Accept mid-points 25.5, 35.5 etc or 24.5, 34.5 etc, leading to answers 70.0 or 69.0 (3sf) respectively. Answers of 69.0, 69.5 or 70.0 (3sf) with no working can be awarded (G1).[5 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) (i) standard deviation is 21.8 cm (G1)
For any other answer without working, award (G0). If working is present then (G0)(AP) is possible.
(ii) \(69.5 + 3 \times 21.8 = 134.9 > 120\) (M1)
no fish (A1)(ft)(G1)
For ‘no fish’ without working, award (G1) regardless of answer to (c)(i). Follow through from (c)(i) only if method is shown. [3 marks]
5 fish are less than 40 cm in length, (M1)
Award (M1) for any of \(\frac{5}{51}\), \(\frac{46}{51}\), 0.098 or 9.8%, 0.902, 90.2% or 5.1 seen.
hence no fine. (A1)(ft)
Note: There is no G mark here and (M0)(A1) is never allowed. The follow-through is from answer in part (a).[2 marks]
(i) and (iii) are correct. (A1)(A1)[2 marks]
Question
The number of bottles of water sold at a railway station on each day is given in the following table.
Write down
(i) the mean temperature;
(ii) the standard deviation of the temperatures.[2]
Write down the correlation coefficient, \(r\), for the variables \(n\) and \(T\).[1]
Comment on your value for \(r\).[2]
The equation of the line of regression for \(n\) on \(T\) is \(n = dT – 100\).
(i) Write down the value of \(d\).
(ii) Estimate how many bottles of water will be sold when the temperature is \({19.6^ \circ }\).[2]
On a day when the temperature was \({36^ \circ }\) Peter calculates that \(314\) bottles would be sold. Give one reason why his answer might be unreliable.[1]
Answer/Explanation
Markscheme
(i) 19.2 (G1)
(ii) 1.45 (G1)[2 marks]
\(r = 0.942\) (G1)[1 mark]
Strong, positive correlation. (A1)(ft)(A1)(ft)[2 marks]
(i) \(d = 11.5\) (G1)
(ii) \(n = 11.5 \times 19.6 – 100\)
\( = 125\) (accept \(126\)) (A1)(ft)
Note: Answer must be a whole number.[2 marks]
It is unreliable to extrapolate outside the values given (outlier). (R1)[1 mark]
Question
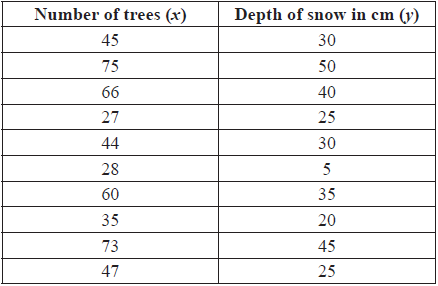
In a mountain region there appears to be a relationship between the number of trees growing in the region and the depth of snow in winter. A set of 10 areas was chosen, and in each area the number of trees was counted and the depth of snow measured. The results are given in the table below.
In a study on \(100\) students there seemed to be a difference between males and females in their choice of favourite car colour. The results are given in the table below. A \(\chi^2\) test was conducted.
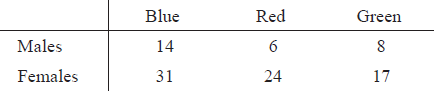
Use your graphic display calculator to find the mean number of trees.[1]
Use your graphic display calculator to find the mean depth of snow.[1]
Use your graphic display calculator to find the standard deviation of the depth of snow.[1]
The covariance, Sxy = 188.5.
Write down the product-moment correlation coefficient, r.[2]
Write down the equation of the regression line of y on x.[2]
If the number of trees in an area is 55, estimate the depth of snow.[2]
Use the equation of the regression line to estimate the depth of snow in an area with 100 trees.[1]
Decide whether the answer in (e)(i) is a valid estimate of the depth of snow in the area. Give a reason for your answer.[2]
Write down the total number of male students.[1]
Show that the expected frequency for males, whose favourite car colour is blue, is 12.6.[2]
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Write down the null hypothesis for this test.[1]
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Write down the number of degrees of freedom.[1]
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Determine whether the null hypothesis should be accepted at the \(5\%\) significance level. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
50 (G1)[1 mark]
30.5 (G1)[1 mark]
12.3 (G1)
Note: Award (A1)(ft) for 13.0 in (iv) but only if 17.7 seen in (a)(ii).[1 mark]
\(r = \frac{{188.5}}{{(16.79 \times 12.33)}}\) (M1)
Note: Award (M1) for using their values in the correct formula.
= 0.911 (accept 0.912, 0.910) (A1)(ft)(G2)[2 marks]
y = 0.669x − 2.95 (G1)(G1)
Note: Award (G1) for 0.669x, (G1) for −2.95. If the answer is not in the form of an equation, award at most (G1)(G0).[2 marks]
Depth = 0.669 × 55 − 2.95 (M1)
= 33.8 (A1)(ft)(G2)(ft)
Note: Follow through from their (c) even if no working seen.[2 marks]
64.0 (accept 63.95, 63.9) (A1)(ft)(G1)(ft)
Note: Follow through from their (c) even if no working seen.[1 mark]
It is not valid. It lies too far outside the values that are given. Or equivalent. (A1)(R1)
Note: Do not award (A1)(R0).[2 marks]
28 (A1)[1 mark]
\(\frac{{28 \times 45}}{{100}}\left( {\frac{{28}}{{100}} \times \frac{{45}}{{100}} \times 100} \right)\) (M1)(A1)(ft)
Note: Award (M1) for correct formula, (A1) for correct substitution.
= 12.6 (AG)
Note: Do not award (A1) unless 12.6 seen.[2 marks]
the favourite car colour is independent of gender. (A1)
Note: Accept there is no association between gender and favourite car colour.
Do not accept ‘not related’ or ‘not correlated’.[1 mark]
\(2\) (A1)[1 marks]
Accept the null hypothesis since \(1.367 < 5.991\) (A1)(ft)(R1)
Note: Allow “Do not reject”. Follow through from their null hypothesis and their critical value.
Full credit for use of \(p\)-values from GDC [\(p = 0.505\)].
Do not award (A1)(R0). Award (R1) for valid comparison.[2 marks]
Question
In an environmental study of plant diversity around a lake, a biologist collected data about the number of different plant species (y) that were growing at different distances (x) in metres from the lake shore.
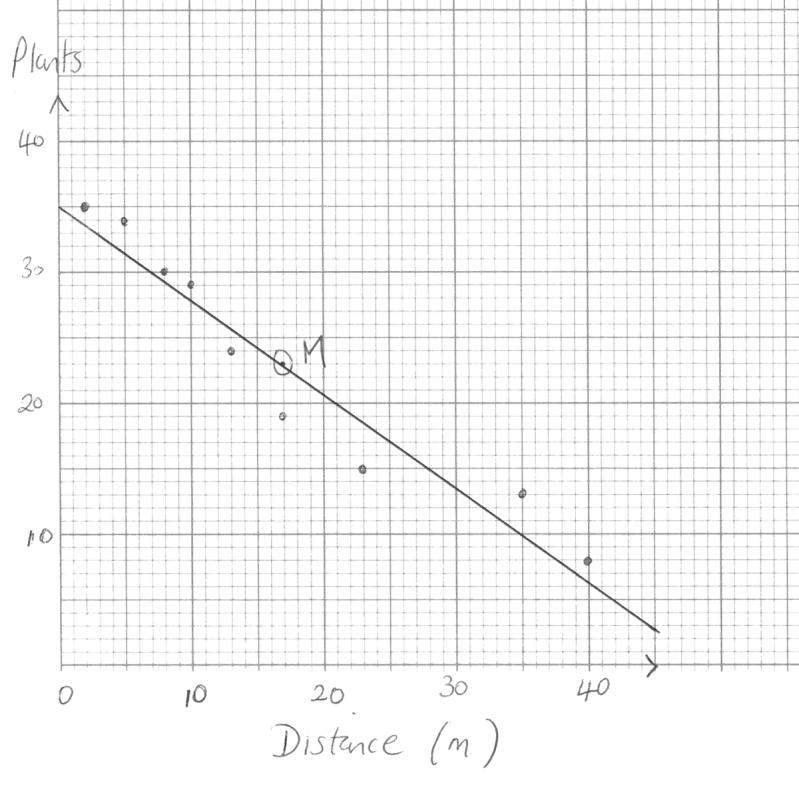
Draw a scatter diagram to show the data. Use a scale of 2 cm to represent 10 metres on the x-axis and 2 cm to represent 10 plant species on the y-axis.[4]
Using your scatter diagram, describe the correlation between the number of different plant species and the distance from the lake shore.[1]
Use your graphic display calculator to write down \(\bar x\), the mean of the distances from the lake shore.[1]
Use your graphic display calculator to write down \(\bar y\), the mean number of plant species.[1]
Plot the point (\(\bar x\), \(\bar y\)) on your scatter diagram. Label this point M.[2]
Write down the equation of the regression line y on x for the above data.[2]
Draw the regression line y on x on your scatter diagram.[2]
Estimate the number of plant species growing 30 metres from the lake shore.[2]
Answer/Explanation
Markscheme
(A1)(A3)
Notes: Award (A1) for scales and labels (accept x/y).
Award (A3) for all points correct.
Award (A2) for 7 or 8 points correct.
Award (A1) for 5 or 6 points correct.
Award at most (A1)(A2) if points are joined up.
If axes are reversed award at most (A0)(A3)(ft).[4 marks]
Negative (A1)[1 mark]
17 (G1)[1 mark]
23 (G1)[1 mark]
Point correctly placed and labelled M (A1)(ft)(A1) Note: Accept an error of ±0.5.[2 marks]
y = –0.708x + 35.0 (G1)(G1)
Note: Award at most (G1)(G0) if y = not seen. Accept 35.[2 marks]
Regression line drawn that passes through M and (0, 35) (A1)(ft)(A1)(ft)
Note: Award (A1) for straight line that passes through M, (A1) for line (extrapolated if necessary) that passes through (0, 35) (accept error of ±1).
If ruler not used, award a maximum of (A1)(A0).[2 marks]
y = –0.708(30) + 35.0 (M1)
= 14 (Accept 13) (A1)(ft)(G2)
OR
Using graph: (M1) for some indication on graph of point, (A1)(ft) for answers. Final answer must be consistent with their graph. (M1)(A1)(ft)(G2)
Note: The final answer must be an integer.[2 marks]
Question
Alex and Kris are riding their bicycles together along a bicycle trail and note the following distance markers at the given times.
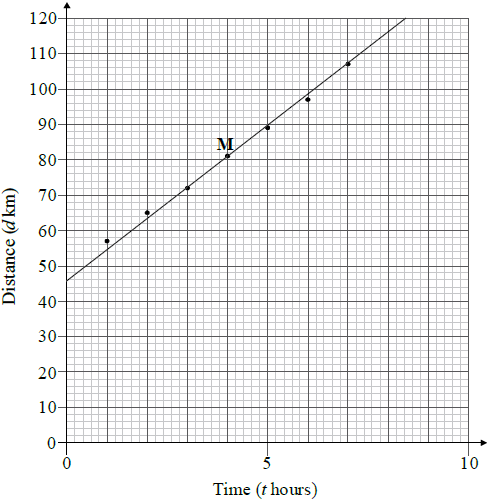
Draw a scatter diagram of the data. Use 1 cm to represent 1 hour and 1 cm to represent 10 km.[3]
Write down for this set of data the mean time, \(\bar t\).[1]
Write down for this set of data the mean distance, \(\bar d\).[1]
Mark and label the point \(M(\bar t,{\text{ }}\bar d)\) on your scatter diagram.[2]
Draw the line of best fit on your scatter diagram.[2]
Using your graph, estimate the time when Alex and Kris pass the 85 km distance marker. Give your answer correct to one decimal place.[2]
Write down the equation of the regression line for the data given.[2]
Using your equation calculate the distance marker passed by the cyclists at 10.3 hours.[2]
Is this estimate of the distance reliable? Give a reason for your answer.[2]
Answer/Explanation
Markscheme
(A1)(A2)
Notes: Award (A1) for axes labelled with d and t and correct scale, (A2) for 6 or 7 points correctly plotted, (A1) for 4 or 5 points, (A0) for 3 or less points correctly plotted. Award at most (A1)(A1) if points are joined up. If axes are reversed award at most (A0)(A2)[3 marks]
\(\bar t = 4\) (G1)[1 mark]
\(\bar d = 81.1\left( {\frac{{568}}{7}} \right)\) (G1)
Note: If answers are the wrong way around award in (i) (G0) and in (ii) (G1)(ft).[1 mark]
Point marked and labelled with M or \(\bar t\), \(\bar d\) on their graph (A1)(ft)(A1)(ft)[2 marks]
Line of best fit drawn that passes through their M and (0, 48) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for straight line that passes through their M, (A1) for line (extrapolated if necessary) that passes through (0, 48).
Accept error of ±3. If ruler not used award a maximum of (A1)(ft)(A0).[2 marks]
4.5h (their answer ±0.2) (M1)(A1)(ft)(G2)
Note: Follow through from their graph. If method shown by some indication on graph of point but answer is incorrect, award (M1)(A0).[2 marks]
d = 8.25t + 48.1 (G1)(G1)
Notes: Award (G1) for 8.25, (G1) for 48.1.
Award at most (G1)(G0) if d = (or y =) is not seen.
Accept d – 81.1 = 8.25(t – 4) or equivalent.[2 marks]
d = 8.25 × 10.3 + 48.1 (M1)
d = 133 km (A1)(ft)(G2)[2 marks]
No (A1)
Outside the set of values of t or equivalent. (R1)
Note: Do not award (A1)(R0).[2 marks]
Question
The heat output in thermal units from burning \(1{\text{ kg}}\) of wood changes according to the wood’s percentage moisture content. The moisture content and heat output of \(10\) blocks of the same type of wood each weighing \(1{\text{ kg}}\) were measured. These are shown in the table.
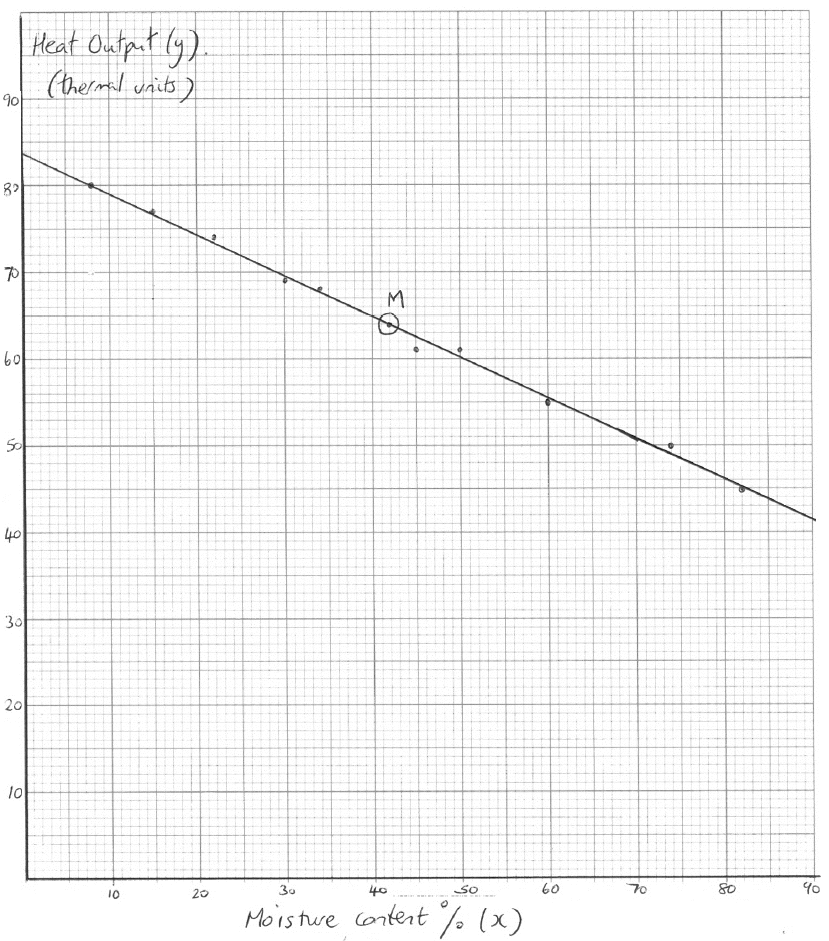
Draw a scatter diagram to show the above data. Use a scale of \(2{\text{ cm}}\) to represent \(10\% \) on the x-axis and a scale of \(2{\text{ cm}}\) to represent \(10\) thermal units on the y-axis.[4]
Write down
(i) the mean percentage moisture content, \(\bar x\) ;
(ii) the mean heat output, \(\bar y\) .[2]
Plot the point \((\bar x{\text{, }}\bar y)\) on your scatter diagram and label this point M .[2]
Write down the product-moment correlation coefficient, \(r\) .[2]
The equation of the regression line \(y\) on \(x\) is \(y = – 0.470x + 83.7\) . Draw the regression line \(y\) on \(x\) on your scatter diagram.[2]
The equation of the regression line \(y\) on \(x\) is \(y = – 0.470x + 83.7\) . Estimate the heat output in thermal units of a \(1{\text{ kg}}\) block of wood that has \(25\% \) moisture content.[2]
The equation of the regression line \(y\) on \(x\) is \(y = – 0.470x + 83.7\) . State, with a reason, whether it is appropriate to use the regression line \(y\) on \(x\) to estimate the heat output in part (f).[2]
Answer/Explanation
Markscheme
(A1) for correct scales and labels
(A3) for all ten points plotted correctly
(A2) for eight or nine points plotted correctly
(A1) for six or seven points plotted correctly (A4)
Note: Award at most (A0)(A3) if axes reversed.[4 marks]
(i) \(\bar x = 42\) (A1)
(ii) \(\bar y = 64\) (A1)[2 marks]
\((\bar x{\text{, }}\bar y)\) plotted on graph and labelled, M (A1)(ft)(A1)
Note: Award (A1)(ft) for position, (A1) for label.[2 marks]
\( – 0.998\) (G2)
Note: Award (G1) for correct sign, (G1) for correct absolute value.[1 mark]
line on graph (A1)(ft)(A1)
Notes: Award (A1)(ft) for line through their M, (A1) for approximately correct intercept (allow between \(83\) and \(85\)). It is not necessary that the line is seen to intersect the \(y\)-axis. The line must be straight for any mark to be awarded.[2 marks]
\(y = – 0.470(25) + 83.7\) (M1)
Note: Award (M1) for substitution into formula or some indication of method on their graph. \(y = – 0.470(0.25) + 83.7\) is incorrect.
\( = 72.0\) (accept \(71.95\) and \(72\)) (A1)(ft)(G2)
Note: Follow through from graph only if they show working on their graph. Accept \(72 \pm 0.5\) .[2 marks]
Yes since \(25\% \) lies within the data set and \(r\) is close to \( – 1\) (R1)(A1)
Note: Accept Yes, since \(r\) is close to \( – 1\)
Note: Do not award (R0)(A1).[2 marks]
Question
Part A
A university required all Science students to study one language for one year. A survey was carried out at the university amongst the 150 Science students. These students all studied one of either French, Spanish or Russian. The results of the survey are shown below.
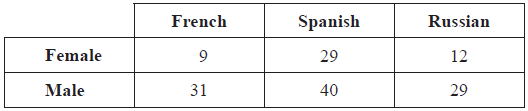
Ludmila decides to use the \({\chi ^2}\) test at the \(5\% \) level of significance to determine whether the choice of language is independent of gender.
At the end of the year, only seven of the female Science students sat examinations in Science and French. The marks for these seven students are shown in the following table.
State Ludmila’s null hypothesis.[1]
Write down the number of degrees of freedom.[1]
Find the expected frequency for the females studying Spanish.[2]
Use your graphic display calculator to find the \({\chi ^2}\) test statistic for this data.[2]
State whether Ludmila accepts the null hypothesis. Give a reason for your answer.[2]
Draw a labelled scatter diagram for this data. Use a scale of \(2{\text{ cm}}\) to represent \(10{\text{ marks}}\) on the \(x\)-axis (\(S\)) and \(10{\text{ marks}}\) on the \(y\)-axis (\(F\)).[4]
Use your graphic calculator to find
(i) \({\bar S}\), the mean of \(S\) ;
(ii) \({\bar F}\), the mean of \(F\) .[2]
Plot the point \({\text{M}}(\bar S{\text{, }}\bar F)\) on your scatter diagram.[1]
Use your graphic display calculator to find the equation of the regression line of \(F\) on \(S\) .[2]
Draw the regression line on your scatter diagram.[2]
Carletta’s mark on the Science examination was \(44\). She did not sit the French examination.
Estimate Carletta’s mark for the French examination.[2]
Monique’s mark on the Science examination was 85. She did not sit the French examination. Her French teacher wants to use the regression line to estimate Monique’s mark.
State whether the mark obtained from the regression line for Monique’s French examination is reliable. Justify your answer.[2]
Answer/Explanation
Markscheme
\({{\text{H}}_0}:\) Choice of language is independent of gender. (A1)
Notes: Do not accept “not related” or “not correlated”.[1 mark]
\(2\) (A1)[1 mark]
\(\frac{{50 \times 69}}{{150}} = 23\) (M1)(A1)(G2)
Notes: Award (M1) for correct substituted formula, (A1) for \(23\).[2 marks]
\({\chi ^2} = 4.77\) (G2)
Notes: If answer is incorrect, award (M1) for correct substitution in the correct formula (all terms).[2 marks]
Accept \({{\text{H}}_0}\) since
\({\chi ^2}_{calc} < {\chi ^2}_{crit}(5.99)\) or \(p\)-value \((0.0923) > 0.05\) (R1)(A1)(ft)
Notes: Do not award (R0)(A1). Follow through from their (d) and (b).
Award (A1) for correct scale and labels.
Award (A3) for all seven points plotted correctly, (A2) for 5 or 6 points plotted correctly, (A1) for 3 or 4 points plotted correctly.(A4)[4 marks]
(i) \({\bar S}= 49.9\), (G1)
(ii) \({\bar F} = 47.3\) (G1)[2 marks]
\({\text{M}}(49.9{\text{, }}47.3)\) plotted on scatter diagram (A1)(ft)
Notes: Follow through from (a) and (b).[1 mark]
\(F = – 0.619S + 78.2\) (G1)(G1)
Notes: Award (G1) for \( – 0.619S\), (G1) for \(78.2\). If the answer is not in the form of an equation, award (G1)(G0). Accept \(y = – 0.619x + 78.2\) .
OR
(F – 47.3 = – 0.619(S – 49.9)) (G1)(G1)
Note: Award (G1) for \( – 0.619\), (G1) for the coordinates of their midpoint used. Follow through from their values in (b).[2 marks]
line drawn on scatter diagram (A1)(ft)(A1)(ft)
Notes: The drawn line must be straight for any marks to be awarded. Award (A1)(ft) passing through their M plotted in (c). Award (A1)(ft) for correct \(y\)-intercept. Follow through from their \(y\)-intercept found in (d).[2 marks]
\(F = – 0.619 \times 44 + 78.2\) (M1)
\(= 51.0\) (allow \(51\) or \(50.9\)) (A1)(ft)(G2)(ft)
Note: Follow through from their equation.
OR
(M1) any indication of an acceptable graphical method. (M1)
(A1)(ft) from their regression line. (A1)(ft)(G2)(ft)[2 marks]
not reliable (A1)
Monique’s score in Science is outside the range of scores used to create the regression line. (R1)
Note: Do not award (A1)(R0).[2 marks]
Question
The table below shows the scores for 12 golfers for their first two rounds in a local golf tournament.
(i) Write down the mean score in Round 1.
(ii) Write down the standard deviation in Round 1.
(iii) Find the number of these golfers that had a score of more than one standard deviation above the mean in Round 1.[5]
Write down the correlation coefficient, r.[2]
Write down the equation of the regression line of y on x.[2]
Another golfer scored 70 in Round 1.
Calculate an estimate of his score in Round 2.[2]
Another golfer scored 89 in Round 1.
Determine whether you can use the equation of the regression line to estimate his score in Round 2. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
(i) \(\frac{{71 + 79 + …}}{{12}}\) (M1)
\(72.4\left( {72.4166…,{\text{ }}\frac{{869}}{{12}}} \right)\) (A1)(G2)
Note: Award (M1) for correct substitution into the mean formula.
(ii) 4.77 (4.76896…) (G1)
(iii) 72.4 + 4.77 = 77.17 (M1)
Note: Award (M1) for adding their mean to their standard deviation.
Two golfers (A1)(ft)(G2)
Note: Follow through from their answers to parts (i) and (ii).[5 marks]
0.990 (0.99014…) (G2)[2 marks]
y = 1.01x + 0.816 (y = 1.01404…x + 0.81618…) (G1)(G1)
Notes: Award (G1) for 1.01x and (G1) for 0.816. If the answer is not an equation award a maximum of (G1)(G0).
OR
y − 74.25 = 1.01(x − 72.4)(y − 74.25 = 1.01404…(x − 72.4166…)) (A1)(A1)
Notes: Award (A1) for 1.01 correctly substituted in the equation, and (A1)(ft) for correct substitution of (72.4, 74.25) in the equation. Follow through from their part (a)(i). If the final answer is not an equation award a maximum of (A1)(A0).[2 marks]
y = 1.01404… × 70 + 0.81618… (M1)
Note: Award (M1) for substitution of 70 into their regression line equation from part (c).
y = 72 (71.7989…) (A1)(ft)(G2)
Note: Follow through from their part (c).[2 marks]
No, equation cannot be (reliably) used as 89 is outside the data range. (A1)(R1)
OR
Yes, but the result is not valid/not reliable as 89 is outside the data range/as we extrapolate (A1)(R1)
Note: Do not award (A1)(R0).[2 marks]
Question
George leaves a cup of hot coffee to cool and measures its temperature every minute. His results are shown in the table below.
Write down the decrease in the temperature of the coffee
(i) during the first minute (between t = 0 and t =1) ;
(ii) during the second minute;
(iii) during the third minute.[3]
Assuming the pattern in the answers to part (a) continues, show that \(k = 19\).[2]
Use the seven results in the table to draw a graph that shows how the temperature of the coffee changes during the first six minutes.
Use a scale of 2 cm to represent 1 minute on the horizontal axis and 1 cm to represent 10 °C on the vertical axis.[4]
The function that models the change in temperature of the coffee is y = p (2−t )+ q.
(i) Use the values t = 0 and y = 94 to form an equation in p and q.
(ii) Use the values t =1 and y = 54 to form a second equation in p and q.[2]
Solve the equations found in part (d) to find the value of p and the value of q.[2]
The graph of this function has a horizontal asymptote.
Write down the equation of this asymptote.[2]
George decides to model the change in temperature of the coffee with a linear function using correlation and linear regression.
Use the seven results in the table to write down
(i) the correlation coefficient;
(ii) the equation of the regression line y on t.[4]
Use the equation of the regression line to estimate the temperature of the coffee at t = 3.[2]
Find the percentage error in this estimate of the temperature of the coffee at t = 3.[2]
Answer/Explanation
Markscheme
(i) 40
(ii) 20
(iii) 10 (A3)
Notes: Award (A0)(A1)(ft)(A1)(ft) for −40, −20, −10.
Award (A1)(A0)(A1)(ft) for 40, 60, 70 seen.
Award (A0)(A0)(A1)(ft) for −40, −60, −70 seen.
\(24 – k = 5\) or equivalent (A1)(M1)
Note: Award (A1) for 5 seen, (M1) for difference from 24 indicated.
\(k = 19\) (AG)
Note: If 19 is not seen award at most (A1)(M0).
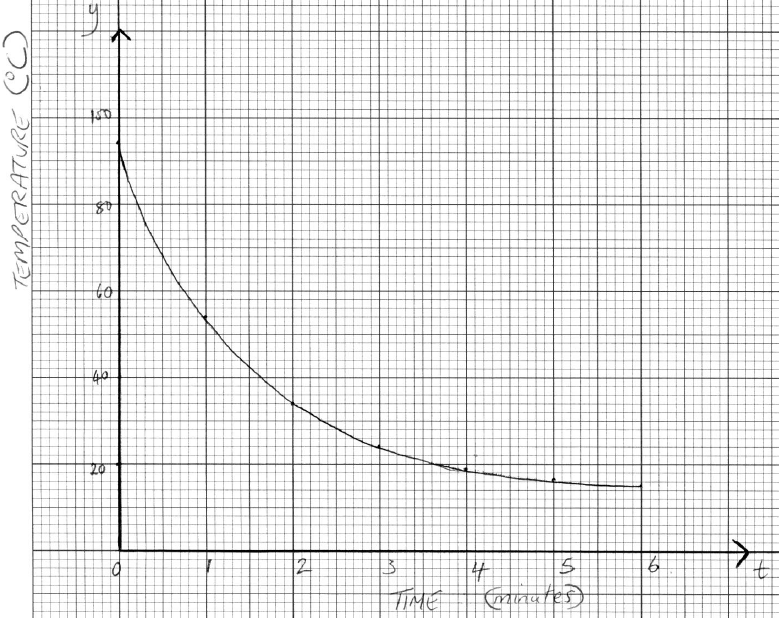(A1)(A1)(A1)(A1)
Note: Award (A1) for scales and labelled axes (t or “time” and y or “temperature”).
Accept the use of x on the horizontal axis only if “time” is also seen as the label.
Award (A2) for all seven points accurately plotted, award (A1) for 5 or 6 points accurately plotted, award (A0) for 4 points or fewer accurately plotted.
Award (A1) for smooth curve that passes through all points on domain [0, 6].
If graph paper is not used or one or more scales is missing, award a maximum of (A0)(A0)(A0)(A1).
(i) \(94 = p + q\) (A1)
(ii) \(54 = 0.5p + q\) (A1)
Note: The equations need not be simplified; accept, for example \(94 = p(2^{-0}) + q\).
p = 80, q = 14 (G1)(G1)(ft)
Note: If the equations have been incorrectly simplified, follow through even if no working is shown.
y = 14 (A1)(A1)(ft)
Note: Award (A1) for y = a constant, (A1) for their 14. Follow through from part (e) only if their q lies between 0 and 15.25 inclusive.
(i) –0.878 (–0.87787…) (G2)
Note: Award (G1) if –0.877 seen only. If negative sign omitted award a maximum of (A1)(A0).
(ii) y = –11.7t + 71.6 (y = –11.6517…t + 71.6336…) (G1)(G1)
Note: Award (G1) for –11.7t, (G1) for 71.6.
If y = is omitted award at most (G0)(G1).
If the use of x in part (c) has not been penalized (the axis has been labelled “time”) then award at most (G0)(G1).
−11.6517…(3) + 71.6339… (M1)
Note: Award (M1) for correct substitution in their part (g)(ii).
= 36.7 (36.6785…) (A1)(ft)(G2)
Note: Follow through from part (g). Accept 36.5 for use of the 3sf answers from part (g).
\(\frac{{36.6785… – 24}}{{24}} \times 100\) (M1)
Note: Award (M1) for their correct substitution in percentage error formula.
= 52.8% (52.82738…) (A1)(ft)(G2)
Note: Follow through from part (h). Accept 52.1% for use of 36.5.
Accept 52.9 % for use of 36.7. If partial working (\(\times 100\) omitted) is followed by their correct answer award (M1)(A1). If partial working is followed by an incorrect answer award (M0)(A0). The percentage sign is not required.
Question
Francesca is a chef in a restaurant. She cooks eight chickens and records their masses and cooking times. The mass m of each chicken, in kg, and its cooking time t, in minutes, are shown in the following table.
Draw a scatter diagram to show the relationship between the mass of a chicken and its cooking time. Use 2 cm to represent 0.5 kg on the horizontal axis and 1 cm to represent 10 minutes on the vertical axis.[4]
Write down for this set of data
(i) the mean mass, \(\bar m\) ;
(ii) the mean cooking time, \(\bar t\) .[2]
Label the point \({\text{M}}(\bar m,\bar t)\) on the scatter diagram.[1]
Draw the line of best fit on the scatter diagram.[2]
Using your line of best fit, estimate the cooking time, in minutes, for a 1.7 kg chicken.[2]
Write down the Pearson’s product–moment correlation coefficient, r .[2]
Using your value for r , comment on the correlation.[2]
The cooking time of an additional 2.0 kg chicken is recorded. If the mass and cooking time of this chicken is included in the data, the correlation is weak.
(i) Explain how the cooking time of this additional chicken might differ from that of the other eight chickens.
(ii) Explain how a new line of best fit might differ from that drawn in part (d).[2]
Answer/Explanation
Markscheme
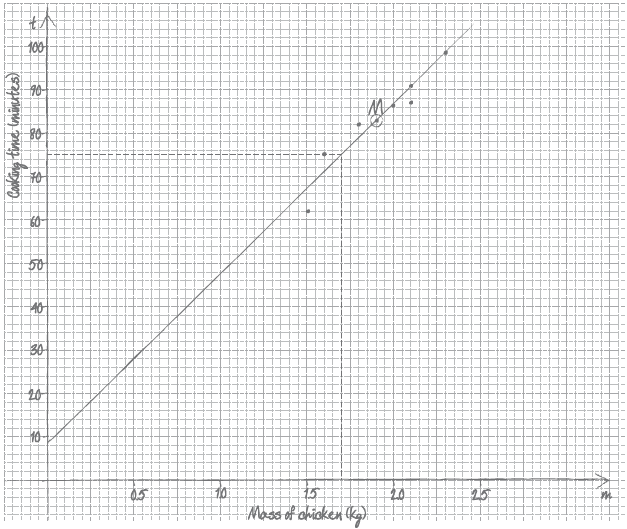
(A1) for correct scales and labels (mass or m on the horizontals axis, time or t on the vertical axis)
(A3) for 7 or 8 correctly placed data points
(A2) for 5 or 6 correctly placed data points
(A1) for 3 or 4 correctly placed data points, (A0) otherwise. (A4)
Note: If axes reversed award at most (A0)(A3)(ft). If graph paper not used, award at most (A1)(A0).
(i) 1.91 (kg) (1.9125 kg) (G1)
(ii) 83 (minutes) (G1)
Their mean point labelled. (A1)(ft)
Note: Follow through from part (b). Accept any clear indication of the mean point. For example: circle around point, (m, t), M , etc.
Line of best fit drawn on scatter diagram. (A1)(ft)(A1)(ft)
Notes:Award (A1)(ft) for straight line through their mean point, (A1)(ft) for line of best fit with intercept 9(±2) . The second (A1)(ft) can be awarded even if the line does not reach the t-axis but, if extended, the t-intercept is correct.
75 (M1)(A1)(ft)(G2)
Notes: Accept 74.77 from the regression line equation. Award (M1) for indication of the use of their graph to get an estimate OR for correct substitution of 1.7 in the correct regression line equation t = 38.5m + 9.32.
0.960 (0.959614…) (G2)
Note: Award (G0)(G1)(ft) for 0.95, 0.959
Strong and positive (A1)(ft)(A1)(ft)
Note: Follow through from their correlation coefficient in part (f).
(i) Cooking time is much larger (or smaller) than the other eight (A1)
(ii) The gradient of the new line of best fit will be larger (or smaller) (A1)
Note: Some acceptable explanations may include but are not limited to:
The line of best fit may be further away from the plotted points
It may be steeper than the previous line (as the mean would change)
The t-intercept of the new line is smaller (larger)
Do not accept vague explanations, like:
The new line would vary
It would not go through all points
It would not fit the patterns
The line may be slightly tilted
Question
The table shows the distance, in km, of eight regional railway stations from a city centre terminus and the price, in \($\), of a return ticket from each regional station to the terminus.
Draw a scatter diagram for the above data. Use a scale of \(1\) cm to represent \(10\) km on the \(x\)-axis and \(1\) cm to represent \(\$10\) on the \(y\)-axis.[4]
Use your graphic display calculator to find
(i) \(\bar x\), the mean of the distances;
(ii) \(\bar y\), the mean of the prices.[2]
Plot and label the point \({\text{M }}(\bar x,{\text{ }}\bar y)\) on your scatter diagram.[1]
Use your graphic display calculator to find
(i) the product–moment correlation coefficient, \(r\,;\)
(ii) the equation of the regression line \(y\) on \(x\).[3]
Draw the regression line \(y\) on \(x\) on your scatter diagram.[2]
A ninth regional station is \(76\) km from the city centre terminus.
Use the equation of the regression line to estimate the price of a return ticket to the city centre terminus from this regional station. Give your answer correct to the nearest \({\mathbf{\$ }}\).[3]
Give a reason why it is valid to use your regression line to estimate the price of this return ticket.[1]
The actual price of the return ticket is \(\$80\).
Using your answer to part (f), calculate the percentage error in the estimated price of the ticket.[2]
Answer/Explanation
Markscheme
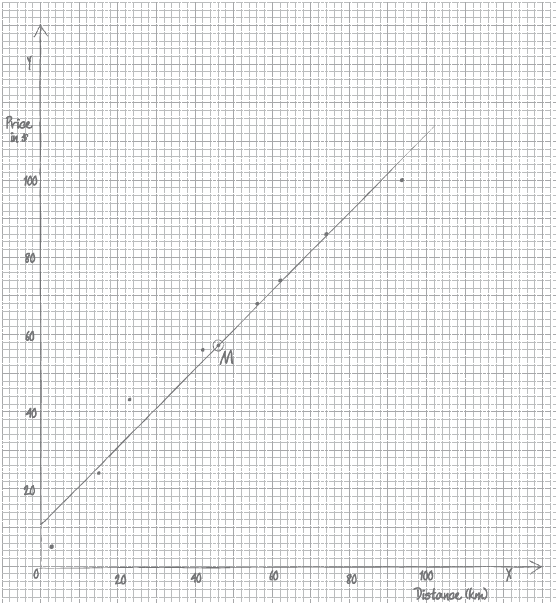(A4)
Notes: Award (A1) for correct scale and labels (accept \(x\) and \(y\)).
Award (A3) for \(7\) or \(8\) points plotted correctly.
Award (A2) for \(5\) or \(6\) points plotted correctly.
Award (A1) for \(3\) or \(4\) points plotted correctly.
Award at most (A1)(A2) if points are joined up.
If axes are reversed, award at most (A0)(A3).
If graph paper is not used, award at most (A1)(A0).[4 marks]
(i) \((\bar x = ){\text{ 46}}\) (G1)
(ii) \((\bar y = ){\text{ 57}}\) (G1)[2 marks]
\({\text{M}} (46, 57)\) plotted and labelled on the scatter diagram (A1)(ft)
Notes: Follow through from their part (b).
Accept \((\bar x,{\text{ }}\bar y)\) as the label.[1 mark]
(i) \(0.986\) \((0.986322…)\) (G1)
(ii) \(y = 1.01x + 10.3\) \((y = 1.01431 \ldots x + 10.3412 \ldots )\) (G1)(G1)
Notes: Award (G1) for \(1.01x\), (G1) for \(10.3\).
Award (G1)(G0) if not written in the form of an equation.
OR
\((y – 57) = 1.01(x – 46)\) \(\left( {y – 57 = 1.01431…(x – 46)} \right)\) (G1)(G1)(ft)
Note: Award (G1) for \(1.01\), (G1) for their \(57\) and \(46\).[3 marks]
straight line drawn on the scatter diagram (A1)(ft)(A1)(ft)
Notes: The line must be straight for either of the two marks to be awarded.
Award (A1)(ft) passing through their \({\text{M}}\) plotted in (c).
Award (A1)(ft) for correct \(y\)-intercept (between \(9\) and \(12\)).
Follow through from their \(y\)-intercept found in part (d).
If part (d) is used, award (A1)(ft) for their intercept \(( \pm 1)\).[2 marks]
\(y = 1.01431… \times 76 + 10.3412…\) (M1)
Note: Award (M1) for substitution of \(76\) into their regression line.
\( = 87.4295…\) (A1)(ft)
Note: Follow through from part (d). If 3 sf values are used the value is \(87.06\).
\(\$87\) (A1)(ft)(G2)
Notes: The final (A1) is awarded for their answer given correct to the nearest dollar.
Method, followed by the answer of \(87\) earns (M1)(G2). It is not necessary to see the interim step.
Where the candidate uses their graph instead of the equation, and arrives at an answer other than \(87\), award, at most, (G1)(ft).
If the candidate uses their graph and arrives at the required answer of \(87\), award (G2)(ft).[3 marks]
\(76\) is within the range of distances given in the data OR the correlation coefficient is close to \(1\). (R1)
Notes: Award (R1) if either condition is given.
Sufficient to indicate that \(76\) is ‘within the data range’ and the correlation is ‘strong’.
Allow \({r^2}\) close to \(1\).
Do not accept “within the range of prices”.[1 mark]
\({\text{Percentage error}} = \frac{{87 – 80}}{{80}} \times 100\) (M1)
Note: Award (M1) for correct substitution into formula.
\(8.75\%\) (A1)(ft)(G2)
Notes: Follow through from their answer to part (f).
Accept either the rounded or unrounded answer to part (f).
If no integer value seen in part (f), follow through from their unrounded answer to part (f).
Answer must be positive.[2 marks]
Question
A biologist is studying the relationship between the number of chirps of the Snowy Tree cricket and the air temperature. He records the chirp rate, \(x\), of a cricket, and the corresponding air temperature, \(T\), in degrees Celsius.
The following table gives the recorded values.
Draw the scatter diagram for the above data. Use a scale of 2 cm for 20 chirps on the horizontal axis and 2 cm for 4°C on the vertical axis.[4]
Use your graphic display calculator to write down the Pearson’s product–moment correlation coefficient, \(r\), between \(x\) and \(T\).[2]
Interpret the relationship between \(x\) and \(T\) using your value of \(r\).[2]
Use your graphic display calculator to write down the equation of the regression line \(T\) on \(x\). Give the equation in the form \(T = ax + b\).[2]
Calculate the air temperature when the cricket’s chirp rate is \(70\).[2]
Given that \(\bar x = 70\), draw the regression line \(T\) on \(x\) on your scatter diagram.[2]
A forest ranger uses her own formula for estimating the air temperature. She counts the number of chirps in 15 seconds, \(z\), multiplies this number by \(0.45\) and then she adds \(10\).
Write down the formula that the forest ranger uses for estimating the temperature, \(T\).
Give the equation in the form \(T = mz + n\).[1]
A cricket makes 20 chirps in 15 seconds.
For this chirp rate
(i) calculate an estimate for the temperature, \(T\), using the forest ranger’s formula;
(ii) determine the actual temperature recorded by the biologist, using the table above;
(iii) calculate the percentage error in the forest ranger’s estimate for the temperature, compared to the actual temperature recorded by the biologist.[6]
Answer/Explanation
Markscheme
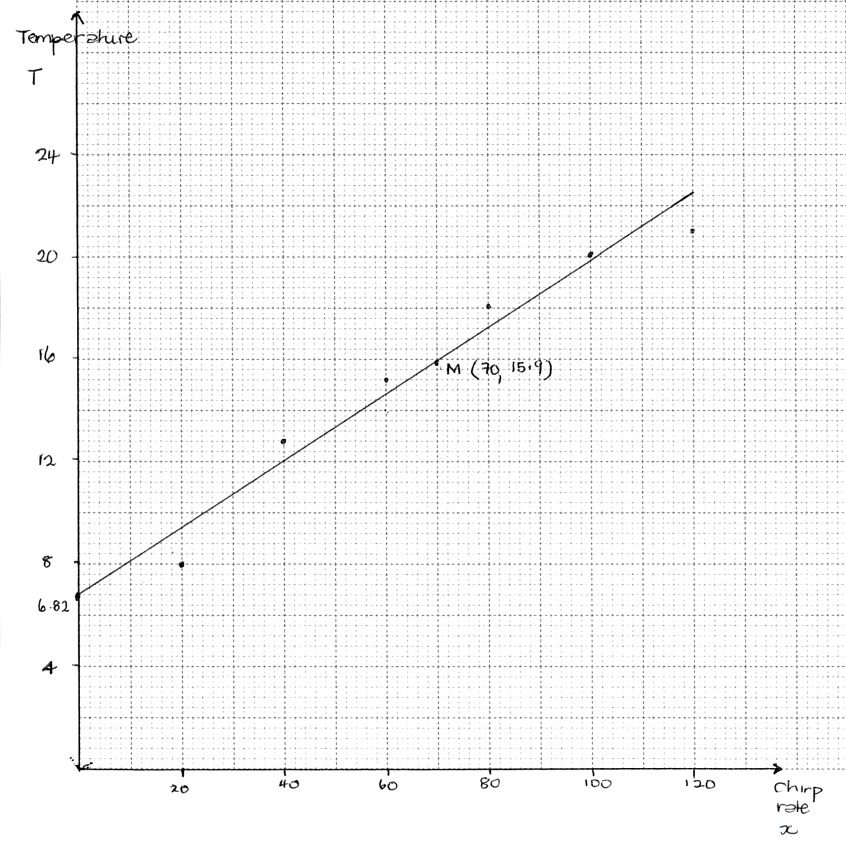
(A4)
Notes: Award (A1) for correct scales and labels.
Award (A3) for all six points correctly plotted,
(A2) for four or five points correctly plotted,
(A1) for two or three points correctly plotted.
Award at most (A0)(A3) if axes reversed.
Accept tolerance for \(T\)-axis.
\({\text{0.977}}\;\;\;{\text{(0.977324}} \ldots {\text{)}}\) (G2)
Notes: Award (G1) for \(0.97\).
(Very) strong positive correlation (A1)(ft)(A1)(ft)
Notes: Award (A1) for (very) strong, (A1) for positive.
Follow through from part (b).
\(T = 0.129x + 6.82\) (G2)
Notes: Award (G1) for \(0.129x\), (G1) for \( + 6.82\).
Award a maximum of (G0)(G1) if the answer is not an equation.
\(0.129 \times 70 + 6.82\) (M1)
Note: Award (M1) for substitution of 70 into their equation of regression line.
OR
\(\frac{{8 + 12.8 + \ldots + 21.1}}{6}\) (M1)
\( = 15.9{\text{ }}(15.85)\) (A1)(ft)(G2)
Note: Follow through from part (d) without working.
regression line through \((70,{\text{ }}15.9)\) (A1)(ft)
Note: Accept \(15.9 \pm 0.2\).
Follow through from part (e).
with \(T\)-intercept, \(6.82\) (A1)(ft)
Note: Follow through from part (d). Accept \(6.82 \pm 0.2\).
In case the regression line is not straight (ruler not used), award (A0)(A1)(ft) if line passes through both their \((70,{\text{ }}15.9)\) and \((0,{\text{ }}6.82)\), otherwise award (A0)(A0).
Do not penalize if line does not intersect the \(T\)-axis.
\(T = 0.45z + 10\) (A1)
(i) \(0.45(20) + 10\) (M1)
Note: Award (M1) for correct substitution of \(20\) into their formula from part (g).
\( = 19\;\;\;(^\circ {\text{C}})\) (A1)(ft)(G2)
Note: Follow through from part (g).
(ii) \( = 18.2\;\;\;(^\circ {\text{C}})\) (A1)
(iii) \(\left| {\frac{{19 – 18.2}}{{18.2}}} \right| \times 100\% \) (M1)(A1)(ft)
Note: Award (M1) for substitution in the percentage error formula, (A1) for correct substitution.
\({\text{4.40% }}\;\;\;{\text{(4.39560}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Follow through from parts (h)(i) and (h)(ii).
Question
The following table shows the number of bicycles, \(x\), produced daily by a factory and their total production cost, \(y\), in US dollars (USD). The table shows data recorded over seven days.
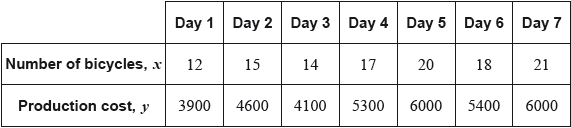
(i) Write down the Pearson’s product–moment correlation coefficient, \(r\), for these data.
(ii) Hence comment on the result.[4]
Write down the equation of the regression line \(y\) on \(x\) for these data, in the form \(y = ax + b\).[2]
Estimate the total cost, to the nearest USD, of producing \(13\) bicycles on a particular day.[3]
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
Explain why the factory does not make a profit when producing \(13\) bicycles on a particular day.[2]
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
(i) Write down an expression for the total selling price of \(x\) bicycles.
(ii) Write down an expression for the profit the factory makes when producing \(x\) bicycles on a particular day.
(iii) Find the least number of bicycles that the factory should produce, on a particular day, in order to make a profit.[5]
Answer/Explanation
Markscheme
(i) \(r = 0.985\;\;\;(0.984905 \ldots )\) (G2)
Notes: If unrounded answer is not seen, award (G1)(G0) for \(0.99\) or \(0.984\). Award (G2) for \(0.98\).
(ii) strong, positive (A1)(A1)
\(y = 259.909 \ldots x + 698.648 \ldots \;\;\;(y = 260x + 699)\) (G1)(G1)
Notes: Award (G1) for \(260x\) and (G1) for \(699\). If the answer is not an equation award a maximum of (G1)(G0).
\(y = 259.909 \ldots \times 13 + 698.648 \ldots \) (M1)
Note: Award (M1) for substitution of \(13\) into their regression line equation from part (b).
\(y = 4077.47 \ldots \) (A1)(ft)(G2)
\(y = 4077{\text{ (USD)}}\) (A1)(ft)
Notes: Follow through from their answer to part (b). If rounded values from part (b) used, answer is \(4079\). Award the final (A1)(ft) for a correct rounding to the nearest USD of their answer. The unrounded answer may not be seen.
If answer is \(4077\) and no working is seen, award (G2).
\(13 \times 304 – (4077.47) = – 125.477 \ldots \;\;\;( – 125)\;\;\;\)OR
\(4077.47 – (13 \times 304) = 125.477 \ldots \;\;\;(125)\) (M1)
Notes: Award (M1) for calculating the difference between \(13 \times 304\) and their answer to part (c).
If rounded values are used in equation, answer is \( – 127\).
profit is negative\(\;\;\;\)OR\(\;\;\;{\text{cost}} > {\text{sales}}\) (A1)
OR
\(13 \times 304 = 3952\) (M1)
Note: Award (M1) for calculating the price of \(13\) bikes.
\(3952 < 4077.47\) (A1)(ft)
Note: Award (A1) for showing \(3952\) is less than their part (c). This may be communicated in words. Follow through from part (c), but only if value is greater than \(3952\).
OR
\(\frac{{4077}}{{13}} = 313.62\) (M1)
Note: Award (M1) for calculating the cost of \(1\) bicycle.
\(313.62 > 304\) (A1)(ft)
Note: Award (A1) for showing \(313.62\) is greater than \(304\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(304\).
OR
\(\frac{{4077}}{{304}} = 13.41\) (M1)
Note: Award (M1) for calculating the number of bicycles that should have been be sold to cover total cost.
\(13.41 > 13\) (A1)(ft)
Note: Award (A1) for showing \(13.41\) is greater than \(13\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(13\).
(i) \(304x\) (A1)
(ii) \(304x – (259.909 \ldots x + 698.648 \ldots )\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for difference between their answers to parts (b) and (e)(i), (A1)(ft) for correct expression.
(iii) \(304x – (259.909 \ldots x + 698.648 \ldots ) > 0\) (M1)
Notes: Award (M1) for comparing their expression in part (e)(ii) to \(0\). Accept an equation. Accept \(3040x – y > 0\) or equivalent.
\(x = 16{\text{ bicycles}}\) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b). Answer must be a positive integer greater than \(13\) for the (A1)(ft) to be awarded.
Award (G1) for an answer of \(15.84\).
Question
For an ecological study, Ernesto measured the average concentration \((y)\) of the fine dust, \({\text{PM}}10\), in the air at different distances \((x)\) from a power plant. His data are represented on the following scatter diagram. The concentration of \({\text{PM}}10\) is measured in micrograms per cubic metre and the distance is measured in kilometres.
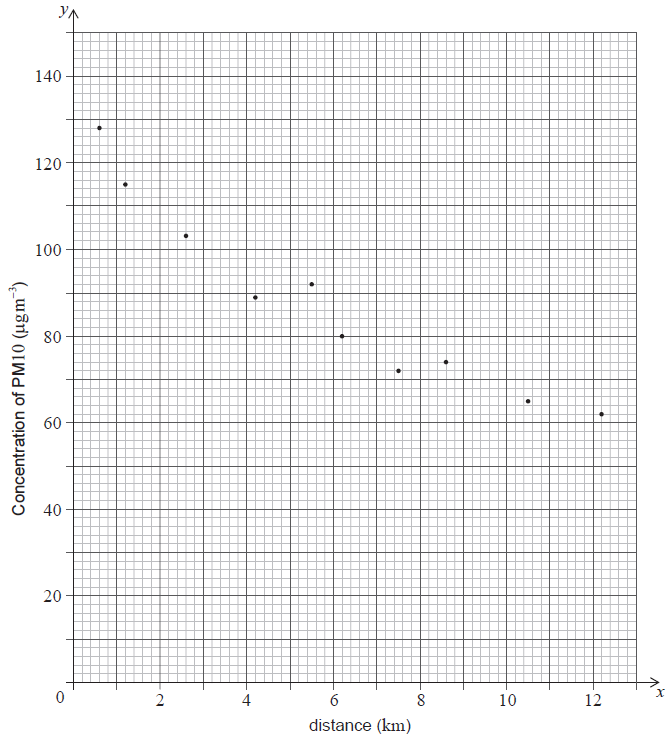
His data are also listed in the following table.
Use the scatter diagram to find the value of \(a\) and of \(b\) in the table.[2]
Calculate
i) \({\bar x}\) , the mean distance from the power plant;
ii) \({\bar y}\) , the mean concentration of \({\text{PM}}10\) ;
iii) \(r\) , the Pearson’s product–moment correlation coefficient.[4]
Write down the equation of the regression line \(y\) on \(x\) .[2]
Ernesto’s school is located \(14\,{\text{km}}\) from the power plant. He uses the equation of the regression line to estimate the concentration of \({\text{PM}}10\) in the air at his school.
i) Calculate the value of Ernesto’s estimate.
ii) State whether Ernesto’s estimate is reliable. Justify your answer.
Answer/Explanation
Markscheme
\(a = 4.2\,;\,\,b = 74\) (A1)(A1)
i) \(5.91\,({\text{km}})\) (A1)(ft)
ii) \(88\) (micrograms per cubic metre) (A1)(ft)
Note: Follow through from part (a) irrespective of working seen.
iii) \( – 0.956\,\,\,\,( – 0.955528…)\) (G2)(ft)
Note: Follow through from part (a) irrespective of working seen.
\(y = – 5.39x + 120\,\,\,\,(y = – 5.38955…x + 119.852…)\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for \( – 5.39\). Award (A1)(ft) for \(120\). If answer is not an equation award at most (A1)(ft)(A0). Follow through from part (a) irrespective of working seen.
i) \( – 5.38955… \times 14 + 119.852…\) (M1)
Note: Award (M1) for correct substitution into their regression line.
\( = 44.4\,\,(44.3984…)\) (A1)(ft)(G2)
Note: Follow through from part (c). Accept \(44.5\,\,(44.54)\) from use of \(3\) significant figure values.
ii) Ernesto’s estimate is not reliable (A1)
this is extrapolation (R1)
OR
\(14\,{\text{km}}\) is not within the range (outside the domain) of distances given (R1)
Note: Do not accept “\(14\) is too high” or “\(14\) is an outlier” or “result not valid/not reliable” if explanation not given. Do not award (A1)(R0). Do not accept reasoning based on the strength of \(r\).
Question
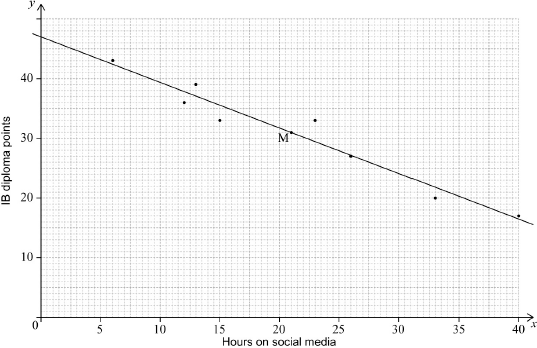
In the month before their IB Diploma examinations, eight male students recorded the number of hours they spent on social media.
For each student, the number of hours spent on social media (\(x\)) and the number of IB Diploma points obtained (\(y\)) are shown in the following table.
Use your graphic display calculator to find
Ten female students also recorded the number of hours they spent on social media in the month before their IB Diploma examinations. Each of these female students spent between 3 and 30 hours on social media.
The equation of the regression line y on x for these ten female students is
\[y = – \frac{2}{3}x + \frac{{125}}{3}.\]
An eleventh girl spent 34 hours on social media in the month before her IB Diploma examinations.
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the \(x\)-axis and 2 cm to represent 10 points on the \(y\)-axis.[4]
(i) \({\bar x}\), the mean number of hours spent on social media;
(ii) \({\bar y}\), the mean number of IB Diploma points.[2]
Plot the point \((\bar x,{\text{ }}\bar y)\) on your scatter diagram and label this point M.[2]
Write down the value of \(r\), the Pearson’s product–moment correlation coefficient, for these data.[2]
Write down the equation of the regression line \(y\) on \(x\) for these eight male students.[2]
Draw the regression line, from part (e), on your scatter diagram.[2]
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.[2]
Write down a reason why this estimate is not reliable.[1]
Answer/Explanation
Markscheme
(A4)
Notes: Award (A1) for correct scale and labelled axes.
Award (A3) for 7 or 8 points correctly plotted,
(A2) for 5 or 6 points correctly plotted,
(A1) for 3 or 4 points correctly plotted.
Award at most (A0)(A3) if axes reversed.
Accept \(x\) and \(y\) sufficient for labelling.
If graph paper is not used, award (A0).
If an inconsistent scale is used, award (A0). Candidates’ points should be read from this scale where possible and awarded accordingly.
A scale which is too small to be meaningful (ie mm instead of cm) earns (A0) for plotted points.[4 marks]
(i) \(\bar x = 21\) (A1)
(ii) \(\bar y = 31\) (A1)[2 marks]
\((\bar x,{\text{ }}\bar y)\) correctly plotted on graph (A1)(ft)
this point labelled M (A1)
Note: Follow through from parts (b)(i) and (b)(ii).
Only accept M for labelling.[2 marks]
\( – 0.973{\text{ }}( – 0.973388 \ldots )\) (G2)
Note: Award (G1) for 0.973, without minus sign.[2 marks]
\(y = – 0.761x + 47.0{\text{ }}(y = – 0.760638 \ldots x + 46.9734 \ldots )\) (A1)(A1)(G2)
Notes: Award (A1) for \( – 0.761x\) and (A1) \( + 47.0\). Award a maximum of (A1)(A0) if answer is not an equation.[2 marks]
line on graph (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for straight line that passes through their M, (A1)(ft) for line (extrapolated if necessary) that passes through \((0,{\text{ }}47.0)\).
If M is not plotted or labelled, follow through from part (e).[2 marks]
\(y = – \frac{2}{3}(34) + \frac{{125}}{3}\) (M1)
Note: Award (M1) for correct substitution.
19 (points) (A1)(G2)[2 marks]
extrapolation (R1)
OR
34 hours is outside the given range of data (R1)
Note: Do not accept ‘outlier’.[1 mark]
Question
The following table shows the average body weight, \(x\), and the average weight of the brain, \(y\), of seven species of mammal. Both measured in kilograms (kg).
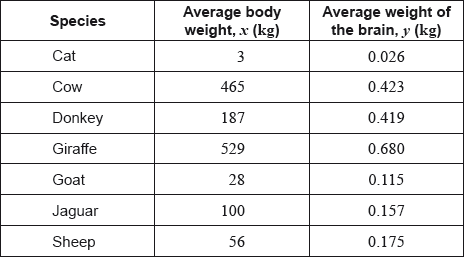
The average body weight of grey wolves is 36 kg.
In fact, the average weight of the brain of grey wolves is 0.120 kg.
The average body weight of mice is 0.023 kg.
Find the range of the average body weights for these seven species of mammal.[2]
For the data from these seven species calculate \(r\), the Pearson’s product–moment correlation coefficient;[2]
For the data from these seven species describe the correlation between the average body weight and the average weight of the brain.[2]
Write down the equation of the regression line \(y\) on \(x\), in the form \(y = mx + c\).[2]
Use your regression line to estimate the average weight of the brain of grey wolves.[2]
Find the percentage error in your estimate in part (d).[2]
State whether it is valid to use the regression line to estimate the average weight of the brain of mice. Give a reason for your answer.[2]
Answer/Explanation
Markscheme
\(529 – 3\) (M1)
\( = 526{\text{ (kg)}}\) (A1)(G2)[2 marks]
\(0.922{\text{ }}(0.921857 \ldots )\) (G2)[2 marks]
(very) strong, positive (A1)(ft)(A1)(ft)
Note: Follow through from part (b)(i).[2 marks]
\(y = 0.000986x + 0.0923{\text{ }}(y = 0.000985837 \ldots x + 0.0923391…)\) (A1)(A1)
Note: Award (A1) for \(0.000986x\), (A1) for 0.0923.
Award a maximum of (A1)(A0) if the answer is not an equation in the form \(y = mx + c\).[2 marks]
\(0.000985837 \ldots (36) + 0.0923391 \ldots \) (M1)
Note: Award (M1) for substituting 36 into their equation.
\(0.128{\text{ (kg) }}\left( {0.127829 \ldots {\text{ (kg)}}} \right)\) (A1)(ft)(G2)
Note: Follow through from part (c). The final (A1) is awarded only if their answer is positive.[2 marks]
\(\left| {\frac{{0.127829 \ldots – 0.120}}{{0.120}}} \right| \times 100\) (M1)
Note: Award (M1) for their correct substitution into percentage error formula.
\(6.52{\text{ }}(\% ){\text{ }}\left( {6.52442…{\text{ }}(\% )} \right)\) (A1)(ft)(G2)
Note: Follow through from part (d). Do not accept a negative answer.[2 marks]
Not valid (A1)
the mouse is smaller/lighter/weighs less than the cat (lightest mammal) (R1)
OR
as it would mean the mouse’s brain is heavier than the whole mouse (R1)
OR
0.023 kg is outside the given data range. (R1)
OR
Extrapolation (R1)
Note: Do not award (A1)(R0). Do not accept percentage error as a reason for validity.[2 marks]
Question
The manager of a folder factory recorded the number of folders produced by the factory (in thousands) and the production costs (in thousand Euros), for six consecutive months.
Every month the factory sells all the folders produced. Each folder is sold for 2.99 Euros.
Draw a scatter diagram for this data. Use a scale of 2 cm for 5000 folders on the horizontal axis and 2 cm for 10 000 Euros on the vertical axis.[4]
Write down, for this set of data the mean number of folders produced, \(\bar x\);[1]
Write down, for this set of data the mean production cost, \(\bar C\).[1]
Label the point \({\text{M}}(\bar x,{\text{ }}\bar C)\) on the scatter diagram.[1]
Use your graphic display calculator to find the Pearson’s product–moment correlation coefficient, \(r\).[2]
State a reason why the regression line \(C\) on \(x\) is appropriate to model the relationship between these variables.[1]
Use your graphic display calculator to find the equation of the regression line \(C\) on \(x\).[2]
Draw the regression line \(C\) on \(x\) on the scatter diagram.[2]
Use the equation of the regression line to estimate the least number of folders that the factory needs to sell in a month to exceed its production cost for that month.[4]
Answer/Explanation
Markscheme
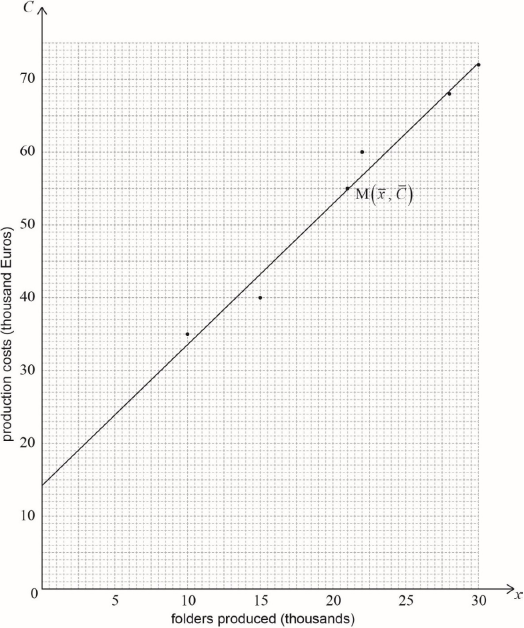(A4)
Notes: Award (A1) for correct scales and labels. Award (A0) if axes are reversed and follow through for their points.
Award (A3) for all six points correctly plotted, (A2) for four or five points correctly plotted, (A1) for two or three points correctly plotted.
If graph paper has not been used, award at most (A1)(A0)(A0)(A0). If accuracy cannot be determined award (A0)(A0)(A0)(A0).[4 marks]
\((\bar x = ){\text{ }}21\) (A1)(G1)[1 mark]
\((\bar C = ){\text{ }}55\) (A1)(G1)
Note: Accept (i) 21000 and (ii) 55000 seen.[1 mark]
their mean point M labelled on diagram (A1)(ft)(G1)
Note: Follow through from part (b).
Award (A1)(ft) if their part (b) is correct and their attempt at plotting \((21,{\text{ }}55)\) in part (a) is labelled M.
If graph paper not used, award (A1) if \((21,{\text{ }}55)\) is labelled. If their answer from part (b) is incorrect and accuracy cannot be determined, award (A0).[1 mark]
\((r = ){\text{ }}0.990{\text{ }}(0.989568 \ldots )\) (G2)
Note: Award (G2) for 0.99 seen. Award (G1) for 0.98 or 0.989. Do not accept 1.00.[2 marks]
the correlation coefficient/r is (very) close to 1 (R1)(ft)
OR
the correlation is (very) strong (R1)(ft)
Note: Follow through from their answer to part (d).
OR
the position of the data points on the scatter graphs suggests that the tendency is linear (R1)(ft)
Note: Follow through from their scatter graph in part (a).[1 mark]
\(C = 1.94x + 14.2{\text{ }}(C = 1.94097 \ldots x + 14.2395 \ldots )\) (G2)
Notes: Award (G1) for \(1.94x\), (G1) for 14.2.
Award a maximum of (G0)(G1) if the answer is not an equation.
Award (G0)(G1)(ft) if gradient and \(C\)-intercept are swapped in the equation.[2 marks]
straight line through their \({\text{M}}(21,{\text{ }}55)\) (A1)(ft)
\(C\)-intercept of the line (or extension of line) passing through \(14.2{\text{ }}( \pm 1)\) (A1)(ft)
Notes: Follow through from part (f). In the event that the regression line is not straight (ruler not used), award (A0)(A1)(ft) if line passes through both their \((21,{\text{ }}55)\) and \((0,{\text{ }}14.2)\), otherwise award (A0)(A0). The line must pass through the midpoint, not near this point. If it is not clear award (A0).
If graph paper is not used, award at most (A1)(ft)(A0).[2 marks]
\(2.99x = 1.94097 \ldots x + 14.2395 \ldots \) (M1)(M1)
Note: Award (M1) for \(2.99x\) seen and (M1) for equating to their equation of the regression line. Accept an inequality sign.
Accept a correct graphical method involving their part (f) and \(2.99x\).
Accept \(C = 2.99x\) drawn on their scatter graph.
\(x = 13.5739 \ldots \) (this step may be implied by their final answer) (A1)(ft)(G2)
\(13\,600{\text{ }}(13\,574)\) (A1)(ft)(G3)
Note: Follow through from their answer to (f). Use of 3 sf gives an answer of \(13\,524\).
Award (G2) for \({\text{13.5739}} \ldots \) or 13.524 or a value which rounds to 13500 seen without workings.
Award the last (A1)(ft) for correct multiplication by 1000 and an answer satisfying revenue > their production cost.
Accept 13.6 thousand (folders).[4 marks]