Question
The diagram shows a pyramid \({\text{VABCD}}\) which has a square base of length \(10{\text{ cm}}\) and edges of length \(13{\text{ cm}}\). \({\text{M}}\) is the midpoint of the side \({\text{BC}}\).
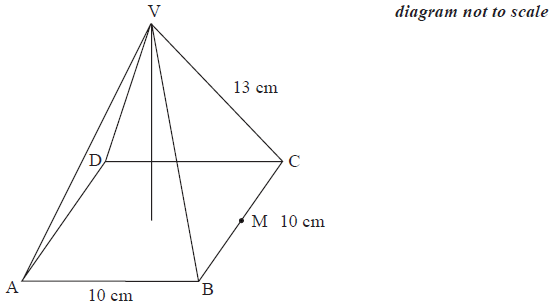
Calculate the length of \({\text{VM}}\).[2]
Calculate the vertical height of the pyramid.[2]
Answer/Explanation
Markscheme
Unit penalty (UP) applies in this question.
\({\text{VM}}^{2} = {13^2} – {5^2}\) (M1)
UP \( = 12{\text{ cm}}\) (A1) (C2)[2 marks]
Unit penalty (UP) applies in this question.
\({h^2} = {12^2} – {5^2}\) (or equivalent) (M1)
UP \( = 10.9{\text{ cm}}\) (A1)(ft) (C2)[2 marks]
Question
The right pyramid shown in the diagram has a square base with sides of length 40 cm. The height of the pyramid is also 40 cm.
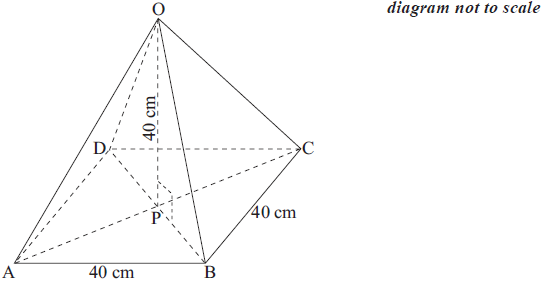
Find the length of OB.[4]
Find the size of angle OBP.[2]
Answer/Explanation
Markscheme
Note: Unit penalty (UP) applies in this part
\({\rm{PB}} = \frac{1}{2}\sqrt {{{40}^2} + {{40}^2}} = \sqrt {800} = 28.28(28.3)\) (M1)(A1)
Note: Award (M1) for correct substitutions, (A1) for correct answer.
(UP) \({\rm{OB}} = \sqrt {{{40}^2} + {{28.28}^2}} = 49.0{\text{ cm }}\left( {\sqrt {2400} {\text{ cm}}} \right)\) (M1)(A1)(ft) (C4)
Note: Award (M1) for correct substitution, can (ft) from any answer to PB.[4 marks]
\({\sin ^{ – 1}}\left( {\frac{{40}}{{49}}} \right)\)
OR
\({\cos ^{ – 1}}\left( {\frac{{28.28}}{{49}}} \right)\)
OR
\({\tan ^{ – 1}}\left( {\frac{{40}}{{28.28}}} \right)\) (M1)
= 54.7 (54.8) (A1)(ft) (C2)
Note: Award (M1) for any correct trig. ratio.
In radians = 0.616, award (M1)(A0).
Note: Common error: (a) \(OB = \sqrt {40^2 + 20^2} = 44.7 {\text{ cm}}\). Award (M0)(A0)(M1), (A1)(ft), and (b) angle OBP = 63.4° (63.5°) (M1)(A1)(ft).[2 marks]
Question
A shipping container is a cuboid with dimensions \({\text{16 m}}\), \({\text{1}}\frac{{\text{3}}}{{\text{4}}}{\text{ m}}\) and \({\text{2}}\frac{{\text{2}}}{{\text{3}}}{\text{ m}}\).
Calculate the exact volume of the container. Give your answer as a fraction.[3]
Jim estimates the dimensions of the container as 15 m, 2 m and 3 m and uses these to estimate the volume of the container.
Calculate the percentage error in Jim’s estimated volume of the container.[3]
Answer/Explanation
Markscheme
\(V = 16 \times 1\frac{3}{4} \times 2\frac{2}{3}\) (M1)
Note: Award (M1) for correct substitution in volume formula. Accept decimal substitution of \(2.66\) or better.
\( = 74.6666{\text{ }} \ldots \) (A1)
\( = {\text{74}}\frac{{\text{2}}}{{\text{3}}}{\text{ }}{{\text{m}}^{\text{3}}}{\text{ }}\left( {\frac{{{\text{224}}}}{{\text{3}}}{\text{ }}{{\text{m}}^{\text{3}}}} \right)\) (A1) (C3)
Note: Correct answer only.[3 marks]
\({\text{% error}} = \frac{{\left( {90 – 74\frac{2}{3}} \right) \times 100}}{{74\frac{2}{3}}}\) (A1)(M1)
Note: Award (A1) for \(90\) seen, or inferred in numerator, (M1) for correct substitution into percentage error formula.
\( = 20.5\) (A1)(ft) (C3)
Note: Accept \( – 20.5\).[3 marks]
Question
A rectangular cuboid has the following dimensions.
Length 0.80 metres (AD)
Width 0.50 metres (DG)
Height 1.80 metres (DC)
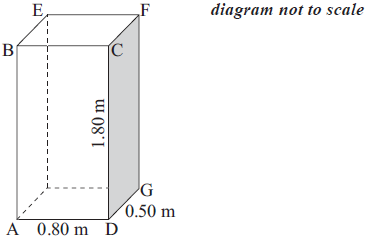
Calculate the length of AG.[2]
Calculate the length of AF.[2]
Find the size of the angle between AF and AG.[2]
Answer/Explanation
Markscheme
\({\text{AG}} = \sqrt {{{0.8}^2} + {{0.5}^2}} \) (M1)
AG = 0.943 m (A1) (C2)[2 marks]
\({\text{AF}} = \sqrt {{\text{A}}{{\text{G}}^2} + {{1.80}^2}} \) (M1)
= 2.03 m (A1)(ft) (C2)
Note: Follow through from their answer to part (a).[2 marks]
\(\cos {\rm{G\hat AF}} = \frac{{0.943(39 \ldots )}}{{2.03(22 \ldots )}}\) (M1)
\(\operatorname{G\hat AF} = 62.3^\circ \) (A1)(ft) (C2)
Notes: Award (M1) for substitution into correct trig ratio.
Accept alternative ratios which give 62.4° or 62.5°.
Follow through from their answers to parts (a) and (b).[2 marks]
Question
A room is in the shape of a cuboid. Its floor measures \(7.2\) m by \(9.6\) m and its height is \(3.5\) m.
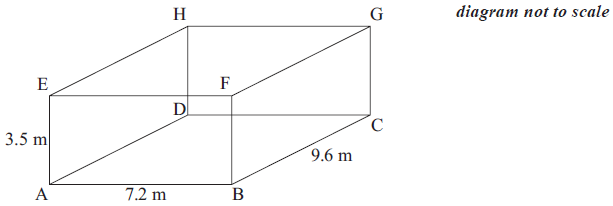
Calculate the length of AC.[2]
Calculate the length of AG.[2]
Calculate the angle that AG makes with the floor.[2]
Answer/Explanation
Markscheme
\({\text{A}}{{\text{C}}^2} = {7.2^2} + {9.6^2}\) (M1)
Note: Award (M1) for correct substitution in Pythagoras Theorem.
\({\text{AC}} = 12{\text{ m}}\) (A1) (C2)[2 marks]
\({\text{A}}{{\text{G}}^2} = {12^2} + {3.5^2}\) (M1)
Note: Award (M1) for correct substitution in Pythagoras Theorem.
\({\text{AG}} = 12.5{\text{ m}}\) (A1)(ft) (C2)
Note: Follow through from their answer to part (a).[2 marks]
\(\tan \theta = \frac{{3.5}}{{12}}\) or \(\sin \theta = \frac{{3.5}}{{12.5}}\) or \(\cos \theta = \frac{{12}}{{12.5}}\) (M1)
Note: Award (M1) for correct substitutions in trig ratio.
\(\theta = {16.3^ \circ }\) (A1)(ft) (C2)
Notes: Follow through from parts (a) and/or part (b) where appropriate. Award (M1)(A0) for use of radians (0.284).[2 marks]
Question
\(75\) metal spherical cannon balls, each of diameter \(10{\text{ cm}}\), were excavated from a Napoleonic War battlefield.
Calculate the total volume of all \(75\) metal cannon balls excavated.[3]
The cannon balls are to be melted down to form a sculpture in the shape of a cone. The base radius of the cone is \(20{\text{ cm}}\).
Calculate the height of the cone, assuming that no metal is wasted.[3]
Answer/Explanation
Markscheme
\(75 \times \frac{4}{3}\pi \times {5^3}\) (M1)(M1)
Notes: Award (M1) for correctly substituted formula of a sphere. Award (M1) for multiplying their volume by \(75\). If \(r = 10\) is used, award (M0)(M1)(A1)(ft) for the answer 314000 cm3 .
\(39300{\text{ c}}{{\text{m}}^3}\) . (A1) (C3)
\(\frac{1}{3}\pi \times {20^2} \times h = 39300\) (M1)(M1)
Notes: Award (M1) for correctly substituted formula of a cone. Award (M1) for equating their volume to their answer to part (a).
\(h = 93.8{\text{ cm}}\) (A1)(ft) (C3)
Notes: Accept the exact value of \(93.75\) . Follow through from their part (a).[3 marks]
Question
An observatory is built in the shape of a cylinder with a hemispherical roof on the top as shown in the diagram. The height of the cylinder is 12 m and its radius is 15 m.
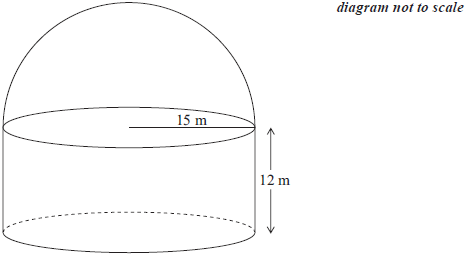
Calculate the volume of the observatory.[4]
The hemispherical roof is to be painted.
Calculate the area that is to be painted.[2]
Answer/Explanation
Markscheme
\(V = \pi {(15)^2}(12) + 0.5 \times \frac{{4\pi {{(15)}^3}}}{3}\) (M1)(M1)(M1)
Note: Award (M1) for correctly substituted cylinder formula, (M1) for correctly substituted sphere formula, (M1) for dividing the sphere formula by 2.
\( = 15550.8 \ldots \)
\( = 15600{\text{ }}{{\text{m}}^3}{\text{ }}(4950\pi {\text{ }}{{\text{m}}^3})\) (A1) (C4)
Notes: The final answer is \(15600{\text{ }}{{\text{m}}^3}\); the units are required. The use of \(\pi = 3.14\) which gives a final answer of \(15 500\) (\(15 543\)) is premature rounding; the final (A1) is not awarded.[4 marks]
\(SA = 0.5 \times 4\pi {\left( {15} \right)^2}\) (M1)
\( = 1413.71 \ldots \)
\( = 1410{\text{ }}{{\text{m}}^2}{\text{ }}(450\pi {\text{ }}{{\text{m}}^2})\) (A1) (C2)
Notes: The final answer is \(1410{\text{ }}{{\text{m}}^2}\) ; do not penalize lack of units if this has been penalized in part (a).[2 marks]
Question
The diagram shows a right triangular prism, ABCDEF, in which the face ABCD is a square.
AF = 8 cm, BF = 9.5 cm, and angle BAF is 90°.
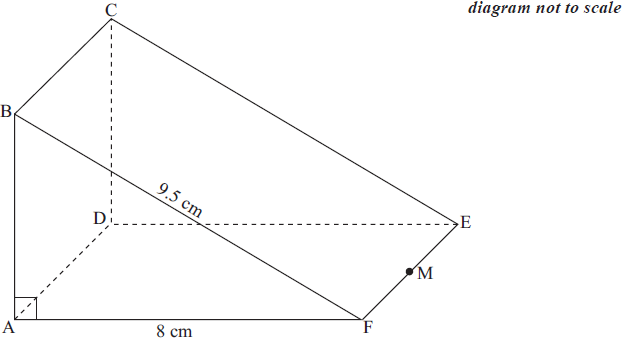
Calculate the length of AB .[2]
M is the midpoint of EF .
Calculate the length of BM .[2]
M is the midpoint of EF .
Find the size of the angle between BM and the face ADEF .[2]
Answer/Explanation
Markscheme
9.52 = 82 + AB2 (M1)
Note: Award (M1) for correct substitution into Pythagoras’ theorem.
AB = 5.12 (cm) (5.12347…) (A1) (C2)[2 marks]
\({\text{BM = }}\sqrt {{{9.5}^2} + {{\left( {\frac{{5.12347…}}{2}} \right)}^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras’ theorem.
= 9.84 (cm) (9.83933…) (A1)(ft) (C2)
Notes: Accept alternative methods. Follow through from their answer to part[2 marks]
sin \({\text{A}}\hat {\rm M}{\text{B = }}\frac{{5.12347…}}{{9.83933…}}\) (M1)
Note: Award (M1) for a correctly substituted trigonometrical equation using \({\text{A}}\hat {\rm M}{\text{B}}\) .
= 31.4 (31.3801…) (A1)(ft) (C2)
Notes: If radians used, the answer will be 0.5476… award (M1)(A0)(ft). Degree symbol ° not required. Follow through from their answers to part (a) and to part (b).[2 marks]
Question
A cuboid has the following dimensions: length = 8.7 cm, width = 5.6 cm and height = 3.4 cm.
Calculate the exact value of the volume of the cuboid, in cm3.[2]
Write your answer to part (a) correct to
(i) one decimal place;
(ii) three significant figures.[2]
Write your answer to part (b)(ii) in the form \(a \times 10^k\), where \(1 \leqslant a < 10 , k \in \mathbb{Z}\).[2]
Answer/Explanation
Markscheme
\({\text{V}} = 8.7 \times 5.6 \times 3.4\) (M1)
Note: Award (M1) for multiplication of the 3 given values.
\(=165.648\) (A1) (C2)
(i) 165.6 (A1)(ft)
Note: Follow through from their answer to part (a).
(ii) 166 (A1)(ft) (C2)
Note: Follow through from their answer to part (a).
\(1.66 \times 10^2\) (A1)(ft)(A1)(ft) (C2)
Notes: Award (A1)(ft) for 1.66, (A1)(ft) for \(10^2\). Follow through from their answer to part (b)(ii) only. The follow through for the index should be dependent on the value of the mantissa in part (c) and their answer to part (b)(ii).
Question
A child’s wooden toy consists of a hemisphere, of radius 9 cm , attached to a cone with the same base radius. O is the centre of the base of the cone and V is vertically above O.
Angle OVB is \({27.9^ \circ }\).
Diagram not to scale.
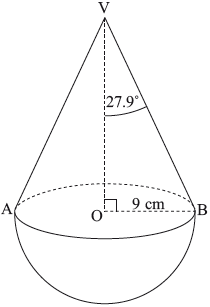
Calculate OV, the height of the cone.[2]
Calculate the volume of wood used to make the toy.[4]
Answer/Explanation
Markscheme
\(\tan 27.9^\circ = \frac{9}{{{\text{OV}}}}\) (M1)
Note: Award (M1) for correct substitution in trig formula.
\({\text{OV}} = 17.0\left( {{\text{cm}}} \right)\left( {16.9980 \ldots } \right)\) (A1) (C2)[2 marks]
\(\frac{{\pi {{(9)}^2}(16.9980 \ldots )}}{3} + \frac{1}{2} \times \frac{{4\pi {{(9)}^3}}}{3}\) (M1)(M1)(M1)
Note: Award (M1) for correctly substituted volume of the cone, (M1) for correctly substituted volume of a sphere divided by two (hemisphere), (M1) for adding the correctly substituted volume of the cone to either a correctly substituted sphere or hemisphere.
\( = 2970{\text{ c}}{{\text{m}}^3}{\text{ (2968.63}} \ldots {\text{)}}\) (A1)(ft) (C4)
Note: The answer is \(2970{\text{ c}}{{\text{m}}^3}\), the units are required.[4 marks]
Question
A right pyramid has apex \({\text{V}}\) and rectangular base \({\text{ABCD}}\), with \({\text{AB}} = 8{\text{ cm}}\), \({\text{BC}} = 6{\text{ cm}}\) and \({\text{VA}} = 13{\text{ cm}}\). The vertical height of the pyramid is \({\text{VM}}\).
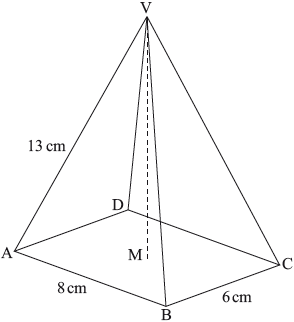
Calculate \({\text{VM}}\).[4]
Calculate the volume of the pyramid.[2]
Answer/Explanation
Markscheme
\({\text{A}}{{\text{C}}^2} = {8^2} + {6^2}\) (M1)
Note: Award (M1) for correct substitution into Pythagoras, or recognition of Pythagorean triple.
\({\text{AC}} = 10\) (A1)
Note: Award (A2) for \({\text{AC}} = 10\;\;\;\)OR\(\;\;\;{\text{AM}} = 5\) with no working seen.
\({\text{V}}{{\text{M}}^2} = {13^2} – {5^2}\) (M1)
Note: Award (M1) for correct second use of Pythagoras, using the result from the first use of Pythagoras.
\({\text{VM}} = 12{\text{ (cm)}}\) (A1) (C4)
Notes: Accept alternative methods and apply the markscheme as follows: Award (M1)(A1) for first correct use of Pythagoras with lengths from the question, (M1) for a correct second use of Pythagoras, consistent with the method chosen, (A1) for correct height.
\(\frac{1}{3} \times 8 \times 6{\kern 1pt} \times 12\) (M1)
Note: Award (M1) for their correct substitutions into volume formula.
\( = 192{\text{ c}}{{\text{m}}^3}\) (A1)(ft) (C2)
Notes: Follow through from part (a), only if working seen.
Question
A cuboid has a rectangular base of width \(x\) cm and length 2\(x\) cm . The height of the cuboid is \(h\) cm . The total length of the edges of the cuboid is \(72\) cm.
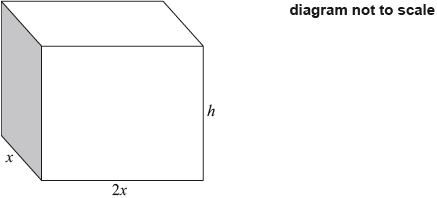
The volume, \(V\), of the cuboid can be expressed as \(V = a{x^2} – 6{x^3}\).
Find the value of \(a\).[3]
Find the value of \(x\) that makes the volume a maximum.[3]
Answer/Explanation
Markscheme
\(72 = 12x + 4h\;\;\;\)(or equivalent) (M1)
Note: Award (M1) for a correct equation obtained from the total length of the edges.
\(V = 2{x^2}(18 – 3x)\) (A1)
\((a = ){\text{ }}36\) (A1) (C3)
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 72x – 18{x^2}\) (A1)
\(72x – 18{x^2} = 0\;\;\;\)OR\(\;\;\;\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) (M1)
Notes: Award (A1) for \( – 18{x^2}\) seen. Award (M1) for equating derivative to zero.
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Note: Follow through from part (a).
OR
Sketch of \(V\) with visible maximum (M1)
Sketch with \(x \geqslant 0,{\text{ }}V \geqslant 0\) and indication of maximum (e.g. coordinates) (A1)(ft)
\((x = ){\text{ 4}}\) (A1)(ft) (C3)
Notes: Follow through from part (a).
Award (M1)(A1)(A0) for \((4,{\text{ }}192)\).
Award (C3) for \(x = 4,{\text{ }}y = 192\).
Question
The diagram shows a triangle \({\rm{ABC}}\). The size of angle \({\rm{C\hat AB}}\) is \(55^\circ\) and the length of \({\rm{AM}}\) is \(10\) m, where \({\rm{M}}\) is the midpoint of \({\rm{AB}}\). Triangle \({\rm{CMB}}\) is isosceles with \({\text{CM}} = {\text{MB}}\).
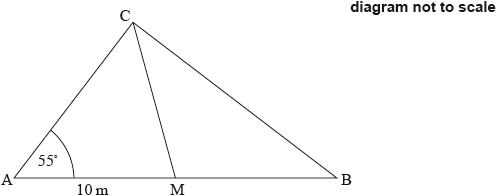
Write down the length of \({\rm{MB}}\).[1]
Find the size of angle \({\rm{C\hat MB}}\).[2]
Find the length of \({\rm{CB}}\).[3]
Answer/Explanation
Markscheme
\(10\) m (A1)(C1)
\({\rm{A\hat MC}} = 70^\circ \;\;\;\)OR\(\;\;\;{\rm{A\hat CM}} = 55^\circ \) (A1)
\({\rm{C\hat MB}} = 110^\circ \) (A1) (C2)
\({\text{C}}{{\text{B}}^2} = {10^2} + {10^2} – 2 \times 10 \times 10 \times \cos 110^\circ \) (M1)(A1)(ft)
Notes: Award (M1) for substitution into the cosine rule formula, (A1)(ft) for correct substitution. Follow through from their answer to part (b).
OR
\(\frac{{{\text{CB}}}}{{\sin 110^\circ }} = \frac{{10}}{{\sin 35^\circ }}\) (M1)(A1)(ft)
Notes: Award (M1) for substitution into the sine rule formula, (A1)(ft) for correct substitution. Follow through from their answer to part (b).
OR
\({\rm{A\hat CB}} = 90^\circ \) (A1)
\(\sin 55^\circ = \frac{{{\text{CB}}}}{{55}}\;\;\;\)OR\(\;\;\;\cos 35^\circ = \frac{{{\text{CB}}}}{{20}}\) (M1)
Note: Award (A1) for some indication that \({\rm{A\hat CB}} = 90^\circ \), (M1) for correct trigonometric equation.
OR
Perpendicular \({\rm{MN}}\) is drawn from \({\rm{M}}\) to \({\rm{CB}}\). (A1)
\(\frac{{\frac{1}{2}{\text{CB}}}}{{10}} = \cos 35^\circ \) (M1)
Note: Award (A1) for some indication of the perpendicular bisector of \({\rm{BC}}\), (M1) for correct trigonometric equation.
\({\text{CB}} = 16.4{\text{ (m)}}\;\;\;\left( {16.3830 \ldots {\text{ (m)}}} \right)\) (A1)(ft)(C3)
Notes: Where a candidate uses \({\rm{C\hat MB}} = 90^\circ \) and finds \({\text{CB}} = 14.1{\text{ (m)}}\) award, at most, (M1)(A1)(A0).
Where a candidate uses \({\rm{C\hat MB}} = 60^\circ \) and finds \({\text{CB}} = 10{\text{ (m)}}\) award, at most, (M1)(A1)(A0).
Question
Assume that the Earth is a sphere with a radius, \(r\) , of \(6.38 \times {10^3}\,{\text{km}}\) .
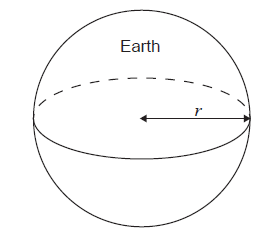
i) Calculate the surface area of the Earth in \({\text{k}}{{\text{m}}^2}\).
ii) Write down your answer to part (a)(i) in the form \(a \times {10^k}\) , where \(1 \leqslant a < 10\) and \(k \in \mathbb{Z}\) .[4]
The surface area of the Earth that is covered by water is approximately \(3.61 \times {10^8}{\text{k}}{{\text{m}}^2}\) .
Calculate the percentage of the surface area of the Earth that is covered by water.[2]
Answer/Explanation
Markscheme
i) \(4\pi {(6.38 \times {10^3})^2}\) (M1)
Note: Award (M1) for correct substitution into the surface area of a sphere formula.
\( = 512\,000\,000\,\,\,(511506576,\,\,162\,817\,600\pi )\) (A1) (C2)
Note: Award at most (M1)(A0) for use of \(3.14\) for \(\pi \), which will give an answer of \(511\,247\,264\).
ii) \(5.12 \times {10^8}\,\,\,(5.11506… \times {10^8},\,\,1.628176\pi \times {10^8})\) (A1)(ft)(A1)(ft) (C2)
Note: Award (A1) for \(5.12\) and (A1) for \( \times {10^8}\).
Award (A0)(A0) for answers of the type: \(5.12 \times {10^7}\).
Follow through from part (a)(i).
\(\frac{{3.61 \times {{10}^8}}}{{5.11506…\,\, \times {{10}^8}}} \times 100\) OR \(\frac{{3.61}}{{5.11506…\,}} \times 100\) OR \(0.705758… \times 100\) (M1)
Note: Award (M1) for correct substitution. Multiplication by \(100\) must be seen.
\( = 70.6\,(\% )\,\,\,\,(70.5758…\,(\% ))\) (A1)(ft) (C2)
Note: Follow through from part (a). Accept the use of \(3\) sf answers, which gives a final answer of \(70.5\,(\% )\,\,\,\,(70.5758…\,(\% ))\) .
Question
A snack container has a cylindrical shape. The diameter of the base is \(7.84\,{\text{cm}}\). The height of the container is \(23.4\,{\text{cm}}\). This is shown in the following diagram.
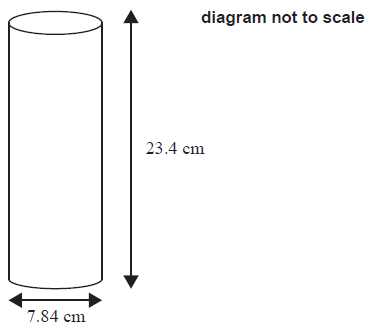
Write down the radius, in \({\text{cm}}\), of the base of the container.[1]
Calculate the area of the base of the container.[2]
Dan is going to paint the curved surface and the base of the snack container.
Calculate the area to be painted.[3]
Answer/Explanation
Markscheme
\(3.92\,({\text{cm}})\) (A1) (C1)
\(\pi \times {3.92^2}\) (M1)
\( = 48.3\,{\text{c}}{{\text{m}}^2}\,\,\,(15.3664\,\pi \,{\text{c}}{{\text{m}}^2},\,\,48.2749…\,{\text{c}}{{\text{m}}^2})\) (A1)(ft) (C2)
Note: Award (M1) for correct substitution in area of circle formula. Follow through from their part (a). The answer is \(48.3\,{\text{c}}{{\text{m}}^2}\), units are required.
\(2 \times \pi \times 3.92 \times 23.4 + 48.3\) (M1)(M1)
\(625\,{\text{c}}{{\text{m}}^2}\,\,\,(624.618…\,{\text{c}}{{\text{m}}^2})\) (A1)(ft) (C3)
Note: Award (M1) for correct substitution in curved surface area formula, (M1) for adding their answer to part (b). Follow through from their parts (a) and (b). The answer is \(625\,{\text{c}}{{\text{m}}^2}\), units are required.
Question
AC is a vertical communications tower with its base at C.
The tower has an observation deck, D, three quarters of the way to the top of the tower, A.
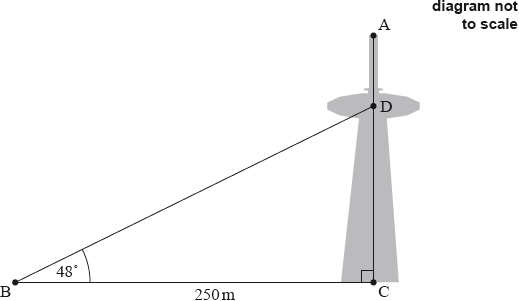
From a point B, on horizontal ground 250 m from C, the angle of elevation of D is 48°.
Calculate CD, the height of the observation deck above the ground.[2]
Calculate the angle of depression from A to B.[4]
Answer/Explanation
Markscheme
\(\tan 48^\circ = \frac{{{\text{CD}}}}{{250}}\) (M1)
Note: Award (M1) for correct substitution into the tangent ratio.
\(({\text{CD}} = ){\text{ }}278{\text{ }}({\text{m}}){\text{ }}(277.653 \ldots )\) (A1) (C2)[2 marks]
\(\tan {\text{ABC (or equivalent)}} = \frac{{\frac{4}{3} \times 277.653 \ldots }}{{250}}\) (M1)(M1)(M1)
Note: Award (M1) for \(\frac{4}{3}\) multiplying their part (a), (M1) for substitution into the tangent ratio, (M1) for correct substitution.
OR
\(90 – {\tan ^{ – 1}}\left( {\frac{{250}}{{\frac{4}{3} \times 277.653 \ldots }}} \right)\) (M1)(M1)(M1)
Note: Award (M1) for \(\frac{4}{3}\) multiplying their part (a), (M1) for substitution into the tangent ratio, (M1) for subtracting from 90 and for correct substitution.
\({\text{(angle of depression}} = {\text{) }}56.0^\circ {\text{ }}(55.9687 \ldots )\) (A1)(ft) (C4)
Note: Follow through from part (a).[4 marks]
Question
A lampshade, in the shape of a cone, has a wireframe consisting of a circular ring and four straight pieces of equal length, attached to the ring at points A, B, C and D.
The ring has its centre at point O and its radius is 20 centimetres. The straight pieces meet at point V, which is vertically above O, and the angle they make with the base of the lampshade is 60°.
This information is shown in the following diagram.
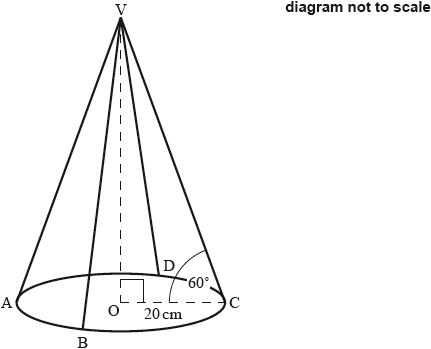
Find the length of one of the straight pieces in the wireframe.[2]
Find the total length of wire needed to construct this wireframe. Give your answer in centimetres correct to the nearest millimetre.[4]
Answer/Explanation
Markscheme
\(\cos 60^\circ = \frac{{20}}{b}\)\(\,\,\,\)OR\(\,\,\,\)\(b = \frac{{20}}{{\cos 60^\circ }}\) (M1)
Note: Award (M1) for correct substitution into a correct trig. ratio.
\((b = ){\text{ 40 (cm)}}\) (A1) (C2)[2 marks]
\(4 \times 40 + 2\pi (20)\) (M1)(M1)
Note: Award (M1) for correct substitution in the circumference of the circle formula, (M1) for adding 4 times their answer to part (a) to their circumference of the circle.
285.6637… (A1)(ft)
Note: Follow through from part (a). This (A1) may be implied by a correct rounded answer.
285.7 (cm) (A1)(ft) (C4)
Notes: Award (A1)(ft) for rounding their answer (consistent with their method) to the nearest millimetre, irrespective of unrounded answer seen.
The final (A1)(ft) is not dependent on any of the previous M marks. It is for rounding their unrounded answer correctly.[4 marks]
Question
A solid right circular cone has a base radius of 21 cm and a slant height of 35 cm.
A smaller right circular cone has a height of 12 cm and a slant height of 15 cm, and is removed from the top of the larger cone, as shown in the diagram.
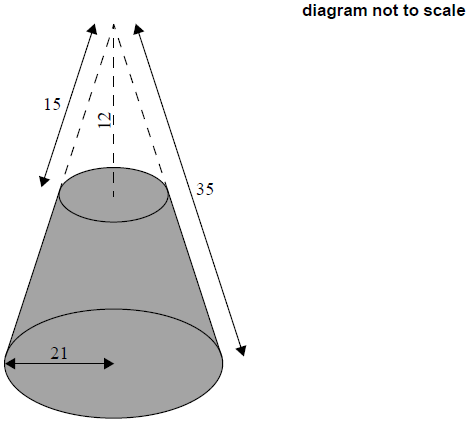
Calculate the radius of the base of the cone which has been removed.[2]
Calculate the curved surface area of the cone which has been removed.[2]
Calculate the curved surface area of the remaining solid.[2]
Answer/Explanation
Markscheme
\(\sqrt {{{15}^2} – {{12}^2}} \) (M1)
Note: Award (M1) for correct substitution into Pythagoras theorem.
OR
\(\frac{{{\text{radius}}}}{{21}} = \frac{{15}}{{35}}\) (M1)
Note: Award (M1) for a correct equation.
= 9 (cm) (A1) (C2)[2 marks]
\(\pi \times 9 \times 15\) (M1)
Note: Award (M1) for their correct substitution into curved surface area of a cone formula.
\( = 424\,\,{\text{c}}{{\text{m}}^2}\,\,\,\,\,\left( {135\pi ,\,\,424.115…{\text{c}}{{\text{m}}^2}} \right)\) (A1)(ft) (C2)
Note: Follow through from part (a).[2 marks]
\(\pi \times 21 \times 35 – 424.115…\) (M1)
Note: Award (M1) for their correct substitution into curved surface area of a cone formula and for subtracting their part (b).
\( = 1880\,\,{\text{c}}{{\text{m}}^2}\,\,\,\,\,\left( {600\pi ,\,\,1884.95…{\text{c}}{{\text{m}}^2}} \right)\) (A1)(ft) (C2)
Note: Follow through from part (b).[2 marks]
Question
The diagram shows a rectangular based right pyramid VABCD in which \({\text{AD}} = 20{\text{ cm}}\), \({\text{DC}} = 15{\text{ cm}}\) and the height of the pyramid, \({\text{VN}} = 30{\text{ cm}}\).
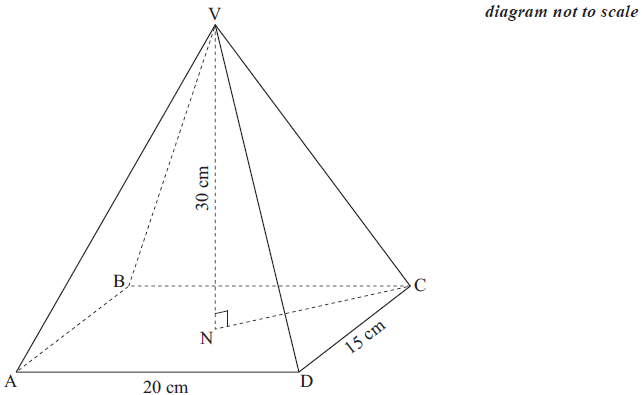
Calculate
(i) the length of AC;
(ii) the length of VC.[4]
Calculate the angle between VC and the base ABCD.[2]
Answer/Explanation
Markscheme
(i) \(\sqrt {{{15}^2} + {{20}^2}} \) (M1)
Note: Award (M1) for correct substitution in Pythagoras Formula.
\({\text{AC}} = 25{\text{ (cm)}}\) (A1) (C2)
(ii) \(\sqrt {{{12.5}^2} + {{30}^2}} \) (M1)
Note: Award (M1) for correct substitution in Pythagoras Formula.
\({\text{VC}} = 32.5{\text{ (cm)}}\) (A1)(ft) (C2)
Note: Follow through from their AC found in part (a).
\(\sin {\text{VCN}} = \frac{{30}}{{32.5}}\) OR \(\tan {\text{VCN}} = \frac{{30}}{{12.5}}\) OR \(\cos {\text{VCN}} = \frac{{12.5}}{{32.5}}\) (M1)
\({ = 67.4^ \circ }\) (\(67.3801 \ldots \)) (A1)(ft) (C2)
Note: Accept alternative methods. Follow through from part (a) and/or part (b).
Question
A child’s toy consists of a hemisphere with a right circular cone on top. The height of the cone is \(12{\text{ cm}}\) and the radius of its base is \(5{\text{ cm}}\) . The toy is painted red.
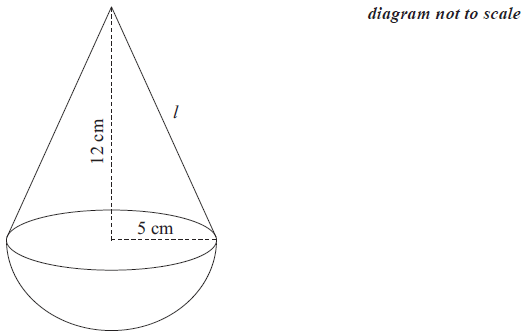
Calculate the length, \(l\), of the slant height of the cone.[2]
Calculate the area that is painted red.[4]
Answer/Explanation
Markscheme
\(\sqrt {{5^2} + {{12}^2}} \) (M1)
Note: Award (M1) for correct substitution in Pythagoras Formula.
=\(13{\text{ (cm)}}\) (A1) (C2)
\({\text{Area}} = 2\pi {(5)^2} + \pi (5)(13)\) (M1)(M1)(M1)
Notes: Award (M1) for surface area of hemisphere, (M1) for surface of cone, (M1) for addition of two surface areas. Follow through from their answer to part (a).
\( = 361{\text{ c}}{{\text{m}}^2}\) (\(361.283 \ldots \)) (A1)(ft) (C4)
Note: The answer is \( 361{\text{ c}}{{\text{m}}^2}\) , the units are required.

