Question
When Geraldine travels to work she can travel either by car (C), bus (B) or train (T). She travels by car on one day in five. She uses the bus 50 % of the time. The probabilities of her being late (L) when travelling by car, bus or train are 0.05, 0.12 and 0.08 respectively.
It is not necessary to use graph paper for this question.
Copy the tree diagram below and fill in all the probabilities, where NL represents not late, to represent this information.
[5]
Find the probability that Geraldine travels by bus and is late.[1]
Find the probability that Geraldine is late.[3]
Find the probability that Geraldine travelled by train, given that she is late.[3]
Sketch the curve of the function \(f (x) = x^3 − 2x^2 + x − 3\) for values of \(x\) from −2 to 4, giving the intercepts with both axes.[3]
On the same diagram, sketch the line \(y = 7 − 2x\) and find the coordinates of the point of intersection of the line with the curve.[3]
Find the value of the gradient of the curve where \(x = 1.7\) .[2]
Answer/Explanation
Markscheme
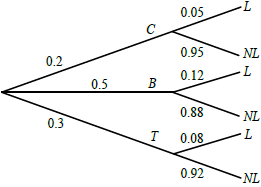
Award (A1) for 0.5 at B, (A1) for 0.3 at T, then (A1) for each correct pair. Accept fractions or percentages. (A5)[5 marks]
0.06 (accept \(0.5 \times 0.12\) or 6%) (A1)(ft)[1 mark]
for a relevant two-factor product, either \(C \times L\) or \(T \times L\) (M1)
for summing three two-factor products (M1)
\((0.2 \times 0.05 + 0.06 + 0.3 \times 0.08)\)
0.094 (A1)(ft)(G2)[3 marks]
\(\frac{{0.3 \times 0.08}}{{0.094}}\) (M1)(A1)(ft)
award (M1) for substituted conditional probability formula seen, (A1)(ft) for correct substitution
= 0.255 (A1)(ft)(G2)[3 marks]
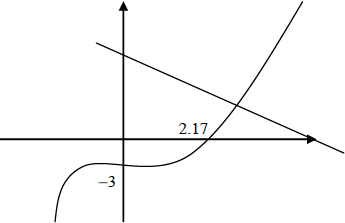(G3)[3 marks]
line drawn with –ve gradient and +ve y-intercept (G1)
(2.45, 2.11) (G1)(G1)[3 marks]
\(f ‘ (1.7) = 3(1.7)^2 – 4(1.7) + 1\) (M1)
award (M1) for substituting in their \(f’ (x)\)
2.87 (A1)(G2)[2 marks]
Question
Consider the functions \(f(x) = \frac{{2x + 3}}{{x + 4}}\) and \(g(x) = x + 0.5\) .
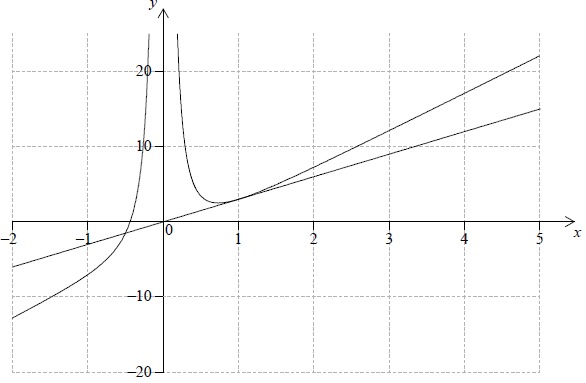
Sketch the graph of the function \(f(x)\), for \( – 10 \leqslant x \leqslant 10\) . Indicating clearly the axis intercepts and any asymptotes.[6]
Write down the equation of the vertical asymptote.[2]
On the same diagram as part (a) sketch the graph of \(g(x) = x + 0.5\) .[2]
Using your graphical display calculator write down the coordinates of one of the points of intersection on the graphs of \(f\) and \(g\), giving your answer correct to five decimal places.[3]
Write down the gradient of the line \(g(x) = x + 0.5\) .[1]
The line \(L\) passes through the point with coordinates \(( – 2{\text{, }} – 3)\) and is perpendicular to the line \(g(x)\) . Find the equation of \(L\).[3]
Answer/Explanation
Markscheme
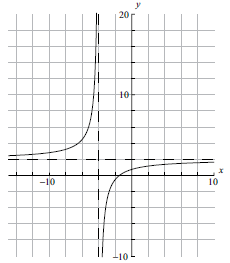(A6)
Notes: (A1) for labels and some idea of scale.
(A1) for \(x\)-intercept seen, (A1) for \(y\)-intercept seen in roughly the correct places (coordinates not required).
(A1) for vertical asymptote seen, (A1) for horizontal asymptote seen in roughly the correct places (equations of the lines not required).
(A1) for correct general shape.[6 marks]
\(x = – 4\) (A1)(A1)(ft)
Note: (A1) for \(x =\), (A1)(ft) for \( – 4\).[2 marks]
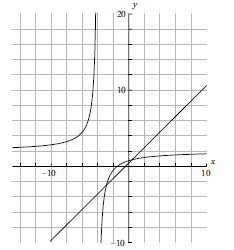(A1)(A1)
Note: (A1) for correct axis intercepts, (A1) for straight line[2 marks]
\(( – 2.85078{\text{, }} – 2.35078)\) OR \((0.35078{\text{, }}0.85078)\) (G1)(G1)(A1)(ft)
Notes: (A1) for \(x\)-coordinate, (A1) for \(y\)-coordinate, (A1)(ft) for correct accuracy. Brackets required. If brackets not used award (G1)(G0)(A1)(ft).
Accept \(x = – 2.85078\), \(y = – 2.35078\) or \(x = 0.35078\), \(y = 0.85078\).[3 marks]
\({\text{gradient}} = 1\) (A1)[1 mark]
\({\text{gradient of perpendicular}} = – 1\) (A1)(ft)
(can be implied in the next step)
\(y = mx + c\)
\( – 3 = – 1 \times – 2 + c\) (M1)
\(c = – 5\)
\(y = – x – 5\) (A1)(ft)(G2)
OR
\(y + 3 = – (x + 2)\) (M1)(A1)(ft)(G2)
Note: Award (G2) for correct answer with no working at all but (A1)(G1) if the gradient is mentioned as \( – 1\) then correct answer with no further working.[3 marks]
Question
Mal is shopping for a school trip. He buys \(50\) tins of beans and \(20\) packets of cereal. The total cost is \(260\) Australian dollars (\({\text{AUD}}\)).
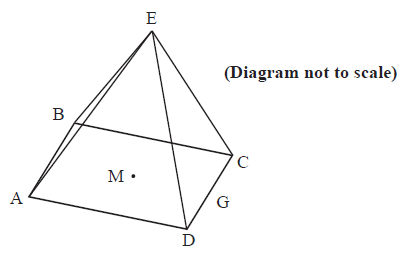
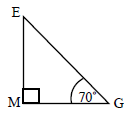
The triangular faces of a square based pyramid, \({\text{ABCDE}}\), are all inclined at \({70^ \circ }\) to the base. The edges of the base \({\text{ABCD}}\) are all \(10{\text{ cm}}\) and \({\text{M}}\) is the centre. \({\text{G}}\) is the mid-point of \({\text{CD}}\).
Write down an equation showing this information, taking \(b\) to be the cost of one tin of beans and \(c\) to be the cost of one packet of cereal in \({\text{AUD}}\).[1]
Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Write down another equation to represent this information.[1]
Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Find the cost of one tin of beans.[2]
(i) Sketch the graphs of the two equations from parts (a) and (b).
(ii) Write down the coordinates of the point of intersection of the two graphs.[4]
Using the letters on the diagram draw a triangle showing the position of a \({70^ \circ }\) angle.[1]
Show that the height of the pyramid is \(13.7{\text{ cm}}\), to 3 significant figures.[2]
Calculate
(i) the length of \({\text{EG}}\);
(ii) the size of angle \({\text{DEC}}\).[4]
Find the total surface area of the pyramid.[2]
Find the volume of the pyramid.[2]
Answer/Explanation
Markscheme
\(50b + 20c = 260\) (A1)[1 mark]
\(12b + 6c = 66\) (A1)[1 mark]
Solve to get \(b = 4\) (M1)(A1)(ft)(G2)
Note: (M1) for attempting to solve the equations simultaneously.[2 marks]
(i)
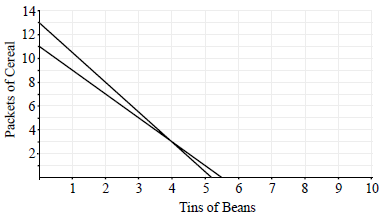(A1)(A1)(A1)
Notes: Award (A1) for labels and some idea of scale, (A1)(ft)(A1)(ft) for each line.
The axis can be reversed.
(ii) \((4,3)\) or \((3,4)\) (A1)(ft)
Note: Accept \(b = 4\), \(c = 3\)[4 marks]
(A1)[1 mark]
\(\tan 70 = \frac{h}{5}\) (M1)
\(h = 5\tan 70 = 13.74\) (A1)
\(h = 13.7{\text{ cm}}\) (AG)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
(i) \({\text{E}}{{\text{G}}^2} = {5^2} + {13.7^2}\) OR \({5^2} + {(5\tan 70)^2}\) (M1)
(UP) \({\text{EG}} = 14.6{\text{ cm}}\) (A1)(G2)
(ii) \({\text{DEC}} = 2 \times {\tan ^{ – 1}}\left( {\frac{5}{{14.6}}} \right)\) (M1)
\( = {37.8^ \circ }\) (A1)(ft)(G2)[4 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Area}} = 10 \times 10 + 4 \times 0.5 \times 10 \times 14.619\) (M1)
(UP) \( = 392{\text{ c}}{{\text{m}}^2}\) (A1)(ft)(G2)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Volume}} = \frac{1}{3} \times 10 \times 10 \times 13.7\) (M1)
(UP) \( = 457{\text{ c}}{{\text{m}}^3}\) (\(458{\text{ c}}{{\text{m}}^3}\)) (A1)(G2)[2 marks]
Question
Consider the function \(f:x \mapsto \frac{{kx}}{{{2^x}}}\).
The cost per person, in euros, when \(x\) people are invited to a party can be determined by the function
\(C(x) = x + \frac{{100}}{x}\)
Given that \(f(1) = 2\), show that \(k = 4\).[2]
Write down the values of \(q\) and \(r\) for the following table.
[2]
As \(x\) increases from \( – 1\), the graph of \(y = f(x)\) reaches a maximum value and then decreases, behaving asymptotically.
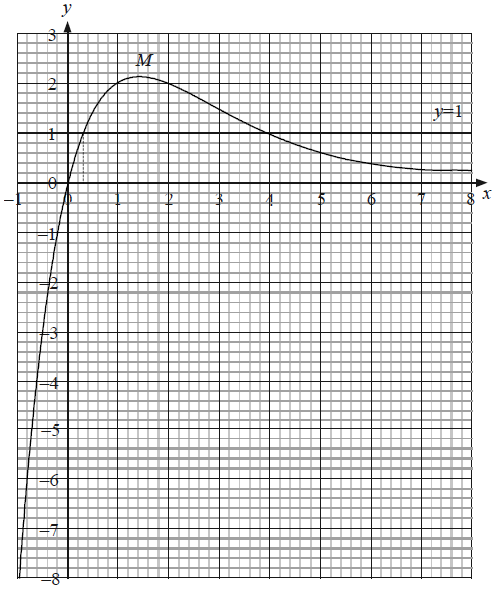
Draw the graph of \(y = f(x)\) for \( – 1 \leqslant x \leqslant 8\). Use a scale of \({\text{1 cm}}\) to represent 1 unit on both axes. The position of the maximum, \({\text{M}}\), the \(y\)-intercept and the asymptotic behaviour should be clearly shown.[4]
Using your graphic display calculator, find the coordinates of \({\text{M}}\), the maximum point on the graph of \(y = f(x)\).[2]
Write down the equation of the horizontal asymptote to the graph of \(y = f(x)\).[2]
(i) Draw and label the line \( y = 1\) on your graph.
(ii) The equation \(f(x) = 1\) has two solutions. One of the solutions is \(x = 4\). Use your graph to find the other solution.[4]
Find \(C'(x)\).[3]
Show that the cost per person is a minimum when \(10\) people are invited to the party.[2]
Calculate the minimum cost per person.[2]
Answer/Explanation
Markscheme
\(f(1) = \frac{k}{{{2^1}}}\) (M1)
Note: (M1) for substituting \(x = 1\) into the formula.
\(\frac{k}{2} = 2\) (M1)
Note: (M1) for equating to 2.
\(k = 4\) (AG)[2 marks]
\(q = 2\), \(r = 0.125\) (A1)(A1)[2 marks]
(A4)
Notes: (A1) for scales and labels.
(A1) for accurate smooth curve passing through \((0, 0)\) drawn at least in the given domain.
(A1) for asymptotic behaviour (curve must not go up or cross the \(x\)-axis).
(A1) for indicating the position of the maximum point.[4 marks]
\({\text{M}}\) (\(1.44\), \(2.12\)) (G1)(G1)
Note: Brackets required, if missing award (G1)(G0). Accept \(x = 1.44\) and \(y = 2.12\).[2 marks]
\(y = 0\) (A1)(A1)
Note: (A1) for ‘\(y = \)’ provided the right hand side is a constant. (A1) for 0.[2 marks]
(i) See graph (A1)(A1)
Note: (A1) for correct line, (A1) for label.
(ii) \(x = 0.3\) (ft) from candidate’s graph. (A2)(ft)
Notes: Accept \( \pm 0.1\) from their x. For \(0.310\) award (G1)(G0). For other answers taken from the GDC and not given correct to 3 significant figures award (G0)(AP)(G0) or (G1)(G0) if (AP) already applied.[4 marks]
\(C'(x) = 1 – \frac{{100}}{{{x^2}}}\) (A1)(A1)(A1)
Note: (A1) for 1, (A1) for \( – 100\) , (A1) for \({x^2}\) as denominator or \({{x^{ – 2}}}\) as numerator. Award a maximum of (A2) if an extra term is seen.[3 marks]
For studying signs of the derivative at either side of \(x = 10\) (M1)
For saying there is a change of sign of the derivative (M1)(AG)
OR
For putting \(x = 10\) into \(C’\) and getting zero (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
OR
For solving \(C'(x) = 0\) and getting \(10\) (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
Note: For a sketch with a clear indication of the minimum or for a table with values of \(x\) at either side of \(x = 10\) award (M1)(M0).[2 marks]
\(C(10) = 10 + \frac{{100}}{{10}}\) (M1)
\(C(10) = 20\) (A1)(G2)[2 marks]
Question
Consider the function \(g(x) = bx – 3 + \frac{1}{{{x^2}}},{\text{ }}x \ne 0\).
Write down the equation of the vertical asymptote of the graph of y = g(x) .[2]
Write down g′(x) .[3]
The line T is the tangent to the graph of y = g(x) at the point where x = 1. The gradient of T is 3.
Show that b = 5.[2]
The line T is the tangent to the graph of y = g(x) at the point where x = 1. The gradient of T is 3.
Find the equation of T.[3]
Using your graphic display calculator find the coordinates of the point where the graph of y = g(x) intersects the x-axis.[2]
(i) Sketch the graph of y = g(x) for −2 ≤ x ≤ 5 and −15 ≤ y ≤ 25, indicating clearly your answer to part (e).
(ii) Draw the line T on your sketch.[6]
Using your graphic display calculator find the coordinates of the local minimum point of y = g(x) .[2]
Write down the interval for which g(x) is increasing in the domain 0 < x < 5 .[2]
Answer/Explanation
Markscheme
x = 0 (A1)(A1)
Notes: Award (A1) for x=constant, (A1) for 0. Award (A0)(A0) if answer is not an equation.[2 marks]
\(b – \frac{2}{{{x^3}}}\) (A1)(A1)(A1)
Note: Award (A1) for b, (A1) for −2, (A1) for \(\frac{1}{{{x^3}}}\) (or x−3). Award at most (A1)(A1)(A0) if extra terms seen.[3 marks]
\(3 = b – \frac{2}{{{{(1)}^3}}}\) (M1)(M1)
Note: Award (M1) for substituting 1 into their gradient function, (M1) for equating their gradient function to 3.
b = 5 (AG)
Note: Award at most (M1)(A0) if final line is not seen or b does not equal 5.[2 marks]
g(1) = 3 or (1, 3) (seen or implied from the line below) (A1)
3 = 3 × 1 + c (M1)
Note: Award (M1) for correct substitution of their point (1, 3) and gradient 3 into equation y = mx + c. Follow through from their point of tangency.
y = 3x (A1)(ft)(G2)
OR
y − 3 = 3(x − 1) (M1)(A1)(ft)(G2)
Note: Award (M1) for substitution of gradient 3 and their point (1, 3) into y − y1 = m(x − x1), (A1)(ft) for correct substitutions. Follow through from their point of tangency. Award at most (A1)(M1)(A0)(ft) if further incorrect working seen.[3 marks]
(−0.439, 0) ((−0.438785…, 0)) (G1)(G1)
Notes: If no parentheses award at most (G1)(G0). Accept x = 0.439, y = 0.[2 marks]
(i)
Award (A1) for labels and some indication of scale in the stated window.
Award (A1) for correct general shape (curve must be smooth and must not cross the y-axis)
Award (A1)(ft) for x-intercept consistent with their part (e).
Award (A1) for local minimum in the first quadrant. (A1)(A1)(A1)(ft)(A1)
(ii) Tangent to curve drawn at approximately x = 1 (A1)(A1)
Note: Award (A1) for a line tangent to curve approximately at x = 1. Must be a straight line for the mark to be awarded. Award (A1)(ft) for line passing through the origin. Follow through from their answer to part (d).[6 marks]
(0.737, 2.53) ((0.736806…, 2.52604…)) (G1)(G1)
Notes: Do not penalize for lack of parentheses if already penalized in (e). Accept x = 0.737, y = 2.53.[2 marks]
0.737 < x < 5 OR (0.737;5) (A1)(A1)(ft)
Notes: Award (A1) for correct strict or weak inequalities with x seen if the interval is given as inequalities, (A1)(ft) for 0.737 and 5 or their value from part (g).[2 marks]
Question
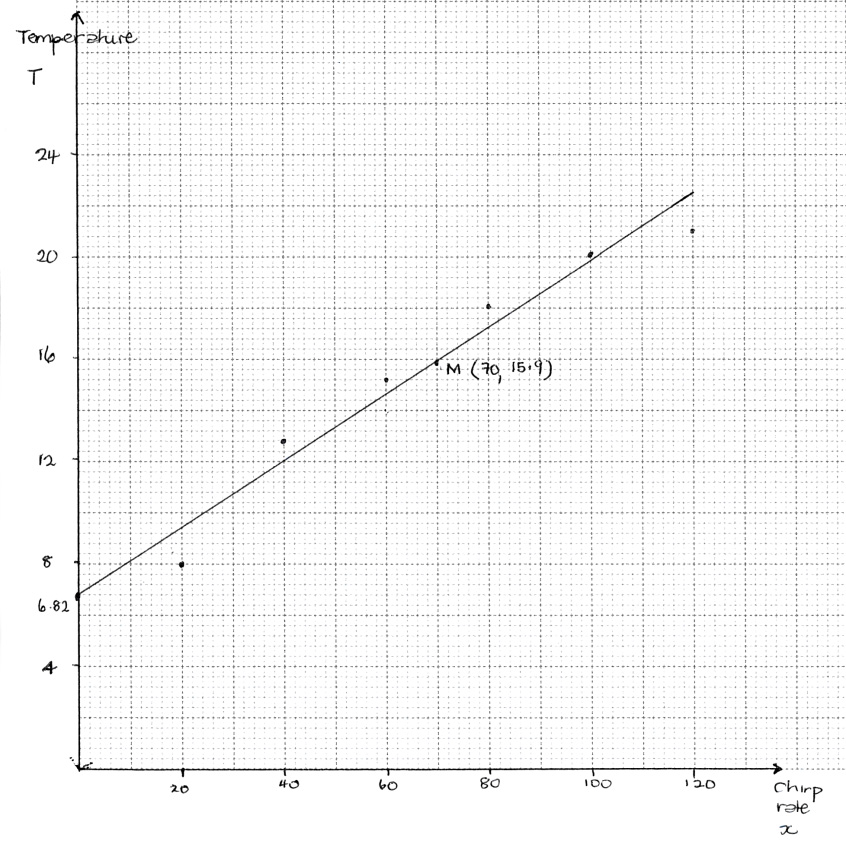
A biologist is studying the relationship between the number of chirps of the Snowy Tree cricket and the air temperature. He records the chirp rate, \(x\), of a cricket, and the corresponding air temperature, \(T\), in degrees Celsius.
The following table gives the recorded values.
Draw the scatter diagram for the above data. Use a scale of 2 cm for 20 chirps on the horizontal axis and 2 cm for 4°C on the vertical axis.[4]
Use your graphic display calculator to write down the Pearson’s product–moment correlation coefficient, \(r\), between \(x\) and \(T\).[2]
Interpret the relationship between \(x\) and \(T\) using your value of \(r\).[2]
Use your graphic display calculator to write down the equation of the regression line \(T\) on \(x\). Give the equation in the form \(T = ax + b\).[2]
Calculate the air temperature when the cricket’s chirp rate is \(70\).[2]
Given that \(\bar x = 70\), draw the regression line \(T\) on \(x\) on your scatter diagram.[2]
A forest ranger uses her own formula for estimating the air temperature. She counts the number of chirps in 15 seconds, \(z\), multiplies this number by \(0.45\) and then she adds \(10\).
Write down the formula that the forest ranger uses for estimating the temperature, \(T\).
Give the equation in the form \(T = mz + n\).[1]
A cricket makes 20 chirps in 15 seconds.
For this chirp rate
(i) calculate an estimate for the temperature, \(T\), using the forest ranger’s formula;
(ii) determine the actual temperature recorded by the biologist, using the table above;
(iii) calculate the percentage error in the forest ranger’s estimate for the temperature, compared to the actual temperature recorded by the biologist.
Answer/Explanation
Markscheme
(A4)
Notes: Award (A1) for correct scales and labels.
Award (A3) for all six points correctly plotted,
(A2) for four or five points correctly plotted,
(A1) for two or three points correctly plotted.
Award at most (A0)(A3) if axes reversed.
Accept tolerance for \(T\)-axis.
\({\text{0.977}}\;\;\;{\text{(0.977324}} \ldots {\text{)}}\) (G2)
Notes: Award (G1) for \(0.97\).
(Very) strong positive correlation (A1)(ft)(A1)(ft)
Notes: Award (A1) for (very) strong, (A1) for positive.
Follow through from part (b).
\(T = 0.129x + 6.82\) (G2)
Notes: Award (G1) for \(0.129x\), (G1) for \( + 6.82\).
Award a maximum of (G0)(G1) if the answer is not an equation.
\(0.129 \times 70 + 6.82\) (M1)
Note: Award (M1) for substitution of 70 into their equation of regression line.
OR
\(\frac{{8 + 12.8 + \ldots + 21.1}}{6}\) (M1)
\( = 15.9{\text{ }}(15.85)\) (A1)(ft)(G2)
Note: Follow through from part (d) without working.
regression line through \((70,{\text{ }}15.9)\) (A1)(ft)
Note: Accept \(15.9 \pm 0.2\).
Follow through from part (e).
with \(T\)-intercept, \(6.82\) (A1)(ft)
Note: Follow through from part (d). Accept \(6.82 \pm 0.2\).
In case the regression line is not straight (ruler not used), award (A0)(A1)(ft) if line passes through both their \((70,{\text{ }}15.9)\) and \((0,{\text{ }}6.82)\), otherwise award (A0)(A0).
Do not penalize if line does not intersect the \(T\)-axis.
\(T = 0.45z + 10\) (A1)
(i) \(0.45(20) + 10\) (M1)
Note: Award (M1) for correct substitution of \(20\) into their formula from part (g).
\( = 19\;\;\;(^\circ {\text{C}})\) (A1)(ft)(G2)
Note: Follow through from part (g).
(ii) \( = 18.2\;\;\;(^\circ {\text{C}})\) (A1)
(iii) \(\left| {\frac{{19 – 18.2}}{{18.2}}} \right| \times 100\% \) (M1)(A1)(ft)
Note: Award (M1) for substitution in the percentage error formula, (A1) for correct substitution.
\({\text{4.40% }}\;\;\;{\text{(4.39560}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Follow through from parts (h)(i) and (h)(ii).
Question
The following table shows the number of bicycles, \(x\), produced daily by a factory and their total production cost, \(y\), in US dollars (USD). The table shows data recorded over seven days.
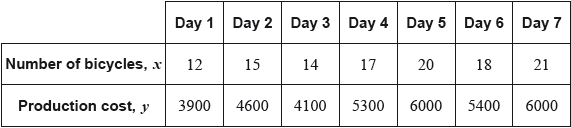
(i) Write down the Pearson’s product–moment correlation coefficient, \(r\), for these data.
(ii) Hence comment on the result.[4]
Write down the equation of the regression line \(y\) on \(x\) for these data, in the form \(y = ax + b\).[2]
Estimate the total cost, to the nearest USD, of producing \(13\) bicycles on a particular day.[3]
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
Explain why the factory does not make a profit when producing \(13\) bicycles on a particular day.[2]
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
(i) Write down an expression for the total selling price of \(x\) bicycles.
(ii) Write down an expression for the profit the factory makes when producing \(x\) bicycles on a particular day.
(iii) Find the least number of bicycles that the factory should produce, on a particular day, in order to make a profit.[5]
Answer/Explanation
Markscheme
(i) \(r = 0.985\;\;\;(0.984905 \ldots )\) (G2)
Notes: If unrounded answer is not seen, award (G1)(G0) for \(0.99\) or \(0.984\). Award (G2) for \(0.98\).
(ii) strong, positive (A1)(A1)
\(y = 259.909 \ldots x + 698.648 \ldots \;\;\;(y = 260x + 699)\) (G1)(G1)
Notes: Award (G1) for \(260x\) and (G1) for \(699\). If the answer is not an equation award a maximum of (G1)(G0).
\(y = 259.909 \ldots \times 13 + 698.648 \ldots \) (M1)
Note: Award (M1) for substitution of \(13\) into their regression line equation from part (b).
\(y = 4077.47 \ldots \) (A1)(ft)(G2)
\(y = 4077{\text{ (USD)}}\) (A1)(ft)
Notes: Follow through from their answer to part (b). If rounded values from part (b) used, answer is \(4079\). Award the final (A1)(ft) for a correct rounding to the nearest USD of their answer. The unrounded answer may not be seen.
If answer is \(4077\) and no working is seen, award (G2).
\(13 \times 304 – (4077.47) = – 125.477 \ldots \;\;\;( – 125)\;\;\;\)OR
\(4077.47 – (13 \times 304) = 125.477 \ldots \;\;\;(125)\) (M1)
Notes: Award (M1) for calculating the difference between \(13 \times 304\) and their answer to part (c).
If rounded values are used in equation, answer is \( – 127\).
profit is negative\(\;\;\;\)OR\(\;\;\;{\text{cost}} > {\text{sales}}\) (A1)
OR
\(13 \times 304 = 3952\) (M1)
Note: Award (M1) for calculating the price of \(13\) bikes.
\(3952 < 4077.47\) (A1)(ft)
Note: Award (A1) for showing \(3952\) is less than their part (c). This may be communicated in words. Follow through from part (c), but only if value is greater than \(3952\).
OR
\(\frac{{4077}}{{13}} = 313.62\) (M1)
Note: Award (M1) for calculating the cost of \(1\) bicycle.
\(313.62 > 304\) (A1)(ft)
Note: Award (A1) for showing \(313.62\) is greater than \(304\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(304\).
OR
\(\frac{{4077}}{{304}} = 13.41\) (M1)
Note: Award (M1) for calculating the number of bicycles that should have been be sold to cover total cost.
\(13.41 > 13\) (A1)(ft)
Note: Award (A1) for showing \(13.41\) is greater than \(13\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(13\).
(i) \(304x\) (A1)
(ii) \(304x – (259.909 \ldots x + 698.648 \ldots )\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for difference between their answers to parts (b) and (e)(i), (A1)(ft) for correct expression.
(iii) \(304x – (259.909 \ldots x + 698.648 \ldots ) > 0\) (M1)
Notes: Award (M1) for comparing their expression in part (e)(ii) to \(0\). Accept an equation. Accept \(3040x – y > 0\) or equivalent.
\(x = 16{\text{ bicycles}}\) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b). Answer must be a positive integer greater than \(13\) for the (A1)(ft) to be awarded.
Award (G1) for an answer of \(15.84\).
Question
Antonio and Barbara start work at the same company on the same day. They each earn an annual salary of \(8000\) euros during the first year of employment. The company gives them a salary increase following the completion of each year of employment. Antonio is paid using plan A and Barbara is paid using plan B.
Plan A: The annual salary increases by \(450\) euros each year.
Plan B: The annual salary increases by \(5\,\% \) each year.
Calculate
i) Antonio’s annual salary during his second year of employment;
ii) Barbara’s annual salary during her second year of employment.[3]
Write down an expression for
i) Antonio’s annual salary during his \(n\) th year of employment;
ii) Barbara’s annual salary during her \(n\) th year of employment.[4]
Determine the number of years for which Antonio’s annual salary is greater than or equal to Barbara’s annual salary.[2]
Both Antonio and Barbara plan to work at the company for a total of \(15\) years.
i) Calculate the total amount that Barbara will be paid during these \(15\) years.
ii) Determine whether Antonio earns more than Barbara during these \(15\) years.[7]
Answer/Explanation
Markscheme
i) \(8450\,({\text{euro}})\) (A1)
ii) \(8000 \times 1.05\) (M1)
Note: Award (M1) for \(8000 \times 1.05\) OR \(\left( {8000 \times 0.05} \right) + 8000.\)
\( = 8400\,({\text{euro}})\) (A1)(G3)
i) \(8000 + 450\,\left( {n – 1} \right)\,\,\,\left( {{\text{accept}}\,\,450\,n + 7550} \right)\) (M1)(A1)
Note: Award (M1) for substitution in arithmetic sequence formula; (A1) for correct substitutions.
ii) \(8000 \times {1.05^{\left( {n – 1} \right)\,}}\) (M1)(A1)
Note: Award (M1) for substitution in arithmetic sequence formula; (A1) for correct substitutions.
\(8000 + 450\,(n – 1) \geqslant 8000 \times {1.05^{n – 1}}\) (M1)
Note: Award (M1) for setting a correct inequality using their expressions for (b)(i) and (b)(ii). Accept an equation.
OR
list of at least 4 correct terms of each sequence (M1)
Note: Award (M1) for correct lists corresponding to their answers for parts (b)(i) and (b)(ii).
\(6\) (A1)(ft)(G2)
Note: Value must be an integer for the final (A1) to be awarded. Follow through from parts (b)(i) and (b)(ii). Award (G1) for a final answer of \(6.70018…\) seen without working.
i) \({S_{15}} = \frac{{8000 \times \left( {{{1.05}^{15}} – 1} \right)}}{{1.05 – 1}}\) (M1)(A1)(ft)
Note: Award (M1) for substitution into geometric series formula and (A1) for correct substitution of \({u_1}\) and their \(r\) from part (b)(ii). Follow through from part (b)(ii).
OR
\(8000 + 8400 + 8820… + 15839.45\) (M1)(A1)(ft)
Note: Follow through from part (b)(ii).
\( = 173\,000\,({\text{euro}})\,\,\,(172629…)\) (A1)(ft)(G2)
ii) \({S_{15}} = \frac{{15}}{2}\left( {2 \times 8000 + 450 \times 14} \right)\) (M1)(A1)(ft)
Note: Award (M1) for substitution into arithmetic series formula and (A1) for correct substitution, using their first term and their last term from part (b)(i), or their \({u_1}\) and \(d\). Follow through from part (b)(i).
OR
\(8000 + 8450 + 8900… + 14300\) (M1)(A1)(ft)
Note: Follow through from part (b)(i).
\( = 167\,000\,({\text{euro}})\,\,\,(167\,250)\) (A1)(ft)(G2)
Antonio does not earn more than Barbara
(his total salary will be less than Barbara’s) (A1)(ft)
Note: Award (A1)(ft) for a final answer that is consistent with their part (d)(i) and (d)(ii). Accept “Barbara earns more”. The final (A1) can only be awarded if two total salaries are seen.
Question
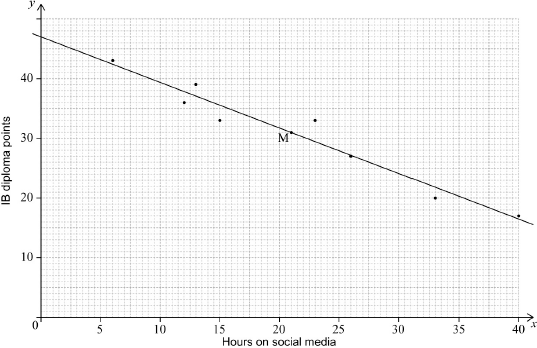
In the month before their IB Diploma examinations, eight male students recorded the number of hours they spent on social media.
For each student, the number of hours spent on social media (\(x\)) and the number of IB Diploma points obtained (\(y\)) are shown in the following table.
Use your graphic display calculator to find
Ten female students also recorded the number of hours they spent on social media in the month before their IB Diploma examinations. Each of these female students spent between 3 and 30 hours on social media.
The equation of the regression line y on x for these ten female students is
\[y = – \frac{2}{3}x + \frac{{125}}{3}.\]
An eleventh girl spent 34 hours on social media in the month before her IB Diploma examinations.
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the \(x\)-axis and 2 cm to represent 10 points on the \(y\)-axis.[4]
(i) \({\bar x}\), the mean number of hours spent on social media;
(ii) \({\bar y}\), the mean number of IB Diploma points.[2]
Plot the point \((\bar x,{\text{ }}\bar y)\) on your scatter diagram and label this point M.[2]
Write down the value of \(r\), the Pearson’s product–moment correlation coefficient, for these data.[2]
Write down the equation of the regression line \(y\) on \(x\) for these eight male students.[2]
Draw the regression line, from part (e), on your scatter diagram.[2]
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.[2]
Write down a reason why this estimate is not reliable.[1]
Answer/Explanation
Markscheme
(A4)
Notes: Award (A1) for correct scale and labelled axes.
Award (A3) for 7 or 8 points correctly plotted,
(A2) for 5 or 6 points correctly plotted,
(A1) for 3 or 4 points correctly plotted.
Award at most (A0)(A3) if axes reversed.
Accept \(x\) and \(y\) sufficient for labelling.
If graph paper is not used, award (A0).
If an inconsistent scale is used, award (A0). Candidates’ points should be read from this scale where possible and awarded accordingly.
A scale which is too small to be meaningful (ie mm instead of cm) earns (A0) for plotted points.[4 marks]
(i) \(\bar x = 21\) (A1)
(ii) \(\bar y = 31\) (A1)[2 marks]
\((\bar x,{\text{ }}\bar y)\) correctly plotted on graph (A1)(ft)
this point labelled M (A1)
Note: Follow through from parts (b)(i) and (b)(ii).
Only accept M for labelling.[2 marks]
\( – 0.973{\text{ }}( – 0.973388 \ldots )\) (G2)
Note: Award (G1) for 0.973, without minus sign.[2 marks]
\(y = – 0.761x + 47.0{\text{ }}(y = – 0.760638 \ldots x + 46.9734 \ldots )\) (A1)(A1)(G2)
Notes: Award (A1) for \( – 0.761x\) and (A1) \( + 47.0\). Award a maximum of (A1)(A0) if answer is not an equation.[2 marks]
line on graph (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for straight line that passes through their M, (A1)(ft) for line (extrapolated if necessary) that passes through \((0,{\text{ }}47.0)\).
If M is not plotted or labelled, follow through from part (e).[2 marks]
\(y = – \frac{2}{3}(34) + \frac{{125}}{3}\) (M1)
Note: Award (M1) for correct substitution.
19 (points) (A1)(G2)[2 marks]
extrapolation (R1)
OR
34 hours is outside the given range of data (R1)
Note: Do not accept ‘outlier’.[1 mark]
Question
The line \({L_1}\) has equation \(2y – x – 7 = 0\) and is shown on the diagram.
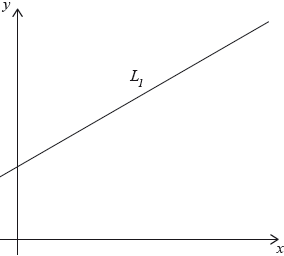
The point A has coordinates \((1,{\text{ }}4)\).
The point C has coordinates \((5,{\text{ }}12)\). M is the midpoint of AC.
The straight line, \({L_2}\), is perpendicular to AC and passes through M.
The point D is the intersection of \({L_1}\) and \({L_2}\).
The length of MD is \(\frac{{\sqrt {45} }}{2}\).
The point B is such that ABCD is a rhombus.
Show that A lies on \({L_1}\).[2]
Find the coordinates of M.[2]
Find the length of AC.[2]
Show that the equation of \({L_2}\) is \(2y + x – 19 = 0\).[5]
Find the coordinates of D.[2]
Write down the length of MD correct to five significant figures.[1]
Find the area of ABCD.[3]
Answer/Explanation
Markscheme
\(2 \times 4 – 1 – 7 = 0\) (or equivalent) (R1)
Note: For (R1) accept substitution of \(x = 1\) or \(y = 4\) into the equation followed by a confirmation that \(y = 4\) or \(x = 1\).
(since the point satisfies the equation of the line,) A lies on \({L_1}\) (A1)
Note: Do not award (A1)(R0).[2 marks]
\(\frac{{1 + 5}}{2}\) OR \(\frac{{4 + 12}}{2}\) seen (M1)
Note: Award (M1) for at least one correct substitution into the midpoint formula.
\((3,{\text{ }}8)\) (A1)(G2)
Notes: Accept \(x = 3,{\text{ }}y = 8\).
Award (M1)(A0) for \(\left( {\frac{{1 + 5}}{2},{\text{ }}\frac{{4 + 12}}{2}} \right)\).
Award (G1) for each correct coordinate seen without working.[2 marks]
\(\sqrt {{{(5 – 1)}^2} + {{(12 – 4)}^2}} \) (M1)
Note: Award (M1) for a correct substitution into distance between two points formula.
\( = 8.94{\text{ }}\left( {4\sqrt 5 ,{\text{ }}\sqrt {80} ,{\text{ }}8.94427 \ldots } \right)\) (A1)(G2)[2 marks]
gradient of \({\text{AC}} = \frac{{12 – 4}}{{5 – 1}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = 2\) (A1)
Note: Award (M1)(A1) for gradient of \({\text{AC}} = 2\) with or without working
gradient of the normal \( = – \frac{1}{2}\) (M1)
Note: Award (M1) for the negative reciprocal of their gradient of AC.
\(y – 8 = – \frac{1}{2}(x – 3)\) OR \(8 = – \frac{1}{2}(3) + c\) (M1)
Note: Award (M1) for substitution of their point and gradient into straight line formula. This (M1) can only be awarded where \( – \frac{1}{2}\) (gradient) is correctly determined as the gradient of the normal to AC.
\(2y – 16 = – (x – 3)\) OR \( – 2y + 16 = x – 3\) OR \(2y = – x + 19\) (A1)
Note: Award (A1) for correctly removing fractions, but only if their equation is equivalent to the given equation.
\(2y + x – 19 = 0\) (AG)
Note: The conclusion \(2y + x – 19 = 0\) must be seen for the (A1) to be awarded.
Where the candidate has shown the gradient of the normal to \({\text{AC}} = – 0.5\), award (M1) for \(2(8) + 3 – 19 = 0\) and (A1) for (therefore) \(2y + x – 19 = 0\).
Simply substituting \((3,{\text{ }}8)\) into the equation of \({L_2}\) with no other prior working, earns no marks.[5 marks]
\((6,{\text{ }}6.5)\) (A1)(A1)(G2)
Note: Award (A1) for 6, (A1) for 6.5. Award a maximum of (A1)(A0) if answers are not given as a coordinate pair. Accept \(x = 6,{\text{ }}y = 6.5\).
Award (M1)(A0) for an attempt to solve the two simultaneous equations \(2y – x – 7 = 0\) and \(2y + x – 19 = 0\) algebraically, leading to at least one incorrect or missing coordinate.[2 marks]
3.3541 (A1)
Note: Answer must be to 5 significant figures.[1 mark]
\(2 \times \frac{1}{2} \times \sqrt {80} \times \frac{{\sqrt {45} }}{2}\) (M1)(M1)
Notes: Award (M1) for correct substitution into area of triangle formula.
If their triangle is a quarter of the rhombus then award (M1) for multiplying their triangle by 4.
If their triangle is a half of the rhombus then award (M1) for multiplying their triangle by 2.
OR
\(\frac{1}{2} \times \sqrt {80} \times \sqrt {45} \) (M1)(M1)
Notes: Award (M1) for doubling MD to get the diagonal BD, (M1) for correct substitution into the area of a rhombus formula.
Award (M1)(M1) for \(\sqrt {80} \times \) their (f).
\( = 30\) (A1)(ft)(G3)
Notes: Follow through from parts (c) and (f).
\(8.94 \times 3.3541 = 29.9856 \ldots \)[3 marks]
Question
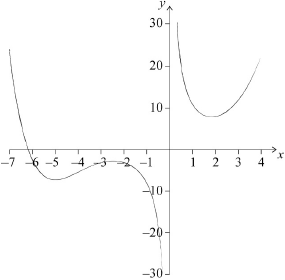
Consider the function \(f(x) = 0.3{x^3} + \frac{{10}}{x} + {2^{ – x}}\).
Consider a second function, \(g(x) = 2x – 3\).
Calculate \(f(1)\).[2]
Sketch the graph of \(y = f(x)\) for \( – 7 \leqslant x \leqslant 4\) and \( – 30 \leqslant y \leqslant 30\).[4]
Write down the equation of the vertical asymptote.[2]
Write down the coordinates of the \(x\)-intercept.[2]
Write down the possible values of \(x\) for which \(x < 0\) and \(f’(x) > 0\).[2]
Find the solution of \(f(x) = g(x)\).[2]
Answer/Explanation
Markscheme
\(0.3{(1)^3} + \frac{{10}}{1} + {2^{ – 1}}\) (M1)
Note: Award (M1) for correct substitution into function.
\( = 10.8\) (A1)(G2)[2 marks]
(A1)(A1)(A1)(A1)
Note: Award (A1) for indication of correct window and labelled axes.
Award (A1) for correct shape and position for \(x < 0\) (with the local maximum, local minimum and \(x\)-intercept in relative approximate location in \({{\text{3}}^{{\text{rd}}}}\) quadrant).
Award (A1) for correct shape and position for \(x > 0\) (with the local minimum in relative approximate location in \({{\text{1}}^{{\text{st}}}}\) quadrant).
Award (A1) for smooth curve with indication of asymptote (graph should not touch \(y\)-axis and should not curve away from the \(y\)-axis). The asymptote is only assessed in this mark.[4 marks]
\(x = 0\) (A2)
Note: Award (A1) for “\(x = {\text{(a constant)}}\)” and (A1) for “\({\text{(a constant)}} = 0\)”.
The answer must be an equation.[2 marks]
\(( – 6.18,{\text{ }}0){\text{ }}( – 6.17516 \ldots ,{\text{ }}0)\) (A1)(A1)
Note: Award (A1) for each correct coordinate. Award (A0)(A1) if parentheses are missing.[2 marks]
\( – 4.99 < x < – 2.47{\text{ }}( – 4.98688 \ldots < x < – 2.46635 \ldots )\) (A1)(A1)
Note: Award (A1) for both correct end points, (A1) for strict inequalities used with 2 endpoints.[2 marks]
\(0.3{x^3} + \frac{{10}}{x} + {2^{ – x}} = 2x – 3\) (M1)
Note: Award (M1) for equating the expressions for \(f\) and \(g\) or for the line \(y = 2x – 3\) sketched (positive gradient, negative \(y\)-intercept) on their graph from part (a).
\((x = ){\text{ }} – 1.34{\text{ }}( – 1.33650 \ldots )\) (A1)(G2)
Note: Award a maximum of (M1)(A0) or (G1) for coordinate pair seen as final answer.[2 marks]