Question
Given \(f (x) = x^2 − 3x^{−1}, x \in {\mathbb{R}}, – 5 \leqslant x \leqslant 5, x \ne 0\),
A football is kicked from a point A (a, 0), 0 < a < 10 on the ground towards a goal to the right of A.
The ball follows a path that can be modelled by part of the graph
\(y = − 0.021x^2 + 1.245x − 6.01, x \in {\mathbb{R}}, y \geqslant 0\).
x is the horizontal distance of the ball from the origin
y is the height above the ground
Both x and y are measured in metres.
Write down the equation of the vertical asymptote.[1]
Find \(f ′(x)\).[2]
Using your graphic display calculator or otherwise, write down the coordinates of any point where the graph of \(y = f (x)\) has zero gradient.[2]
Write down all intervals in the given domain for which \(f (x)\) is increasing.[3]
Using your graphic display calculator or otherwise, find the value of a.[1]
Find \(\frac{{dy}}{{dx}}\).[2]
(i) Use your answer to part (b) to calculate the horizontal distance the ball has travelled from A when its height is a maximum.
(ii) Find the maximum vertical height reached by the football.[4]
Draw a graph showing the path of the football from the point where it is kicked to the point where it hits the ground again. Use 1 cm to represent 5 m on the horizontal axis and 1 cm to represent 2 m on the vertical scale.[4]
The goal posts are 35 m from the point where the ball is kicked.
At what height does the ball pass over the goal posts?[2]
Answer/Explanation
Markscheme
equation of asymptote is x = 0 (A1)
(Must be an equation.)[1 mark]
\(f ‘(x) = 2x + 3x^{-2}\) (or equivalent) (A1) for each term (A1)(A1)[2 marks]
stationary point (–1.14, 3.93) (G1)(G1)(ft)
(-1,4) or similar error is awarded (G0)(G1)(ft). Here and also as follow through in part (d) accept exact values \( – {\left( {\frac{3}{2}} \right)^{\frac{1}{3}}}\)for the x coordinate and \(3{\left( {\frac{3}{2}} \right)^{\frac{2}{3}}}\) for the y coordinate.
OR \(2x + \frac{3}{{{x^2}}} = 0\) or equivalent
Correct coordinates as above (M1)
Follow through from candidate’s \(f ′(x)\). (A1)(ft)[2 marks]
In all alternative answers for (d), follow through from candidate’s x coordinate in part (c).
Alternative answers include:
–1.14 ≤ x < 0, 0 < x < 5 (A1)(A1)(ft)(A1)
OR [–1.14,0), (0,5)
Accept alternative bracket notation for open interval ] [. (Union of these sets is not correct, award (A2) if all else is right in this case.)
OR \( – 1.14 \leqslant x < 5,x \ne 0\)
In all versions 0 must be excluded (A1). -1.14 must be the left bound . 5 must be the right bound (A1). For \(x \geqslant – 1.14\) or \(x > – 1.14\) alone, award (A1). For \( – 1.4 \leqslant x < 0\) together with \(x > 0\) award (A2).[3 marks]
a = 5.30 (3sf) (Allow (5.30, 0) but 5.3 receives an (AP).) (A1)[1 mark]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 0.042x + 1.245\) (A1) for each term. (A1)(A1)[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) Maximum value when \(f ‘ (x) = 0\), \( – 0.042x + 1.245 = 0\), (M1)
(M1) is for either of the above but at least one must be seen.
(x = 29.6.)
Football has travelled 29.6 – 5.30 = 24.3 m (3sf) horizontally. (A1)(ft)
For answer of 24.3 m with no working or for correct subtraction of 5.3 from candidate’s x-coordinate at the maximum (if not 29.6), award (A1)(d).(UP) (ii) Maximum vertical height, f (29.6) = 12.4 m (M1)(A1)(ft)(G2)
(M1) is for substitution into f of a value seen in part (c)(i). f(24.3) with or without evaluation is awarded (M1)(A0). For any other value without working, award (G0). If lines are seen on the graph in part (d) award (M1) and then (A1) for candidate’s value \( \pm 0.5\) (3sf not required.)[4 marks]
(not to scale)
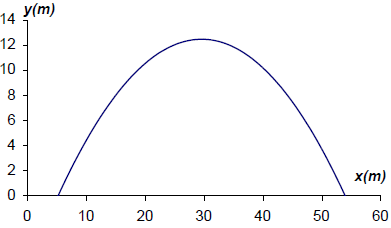(A1)(A1)(A1)(ft)(A1)(ft)
Award (A1) for labels (units not required) and scale, (A1)(ft) for max(29.6,12.4), (A1)(ft) for x-intercepts at 5.30 and 53.9, (all coordinates can be within 0.5), (A1) for well-drawn parabola ending at the x-intercepts.[4 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) f (40.3) = 10.1 m (3sf).
Follow through from (a). If graph used, award (M1) for lines drawn and (A1) for candidate’s value \( \pm 0.5\). (3sf not required). (M1)(A1)(ft)(G2)[2 marks]
Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
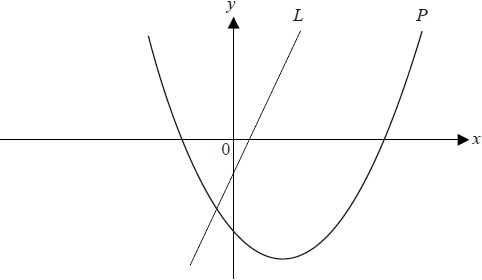
Find the gradient of the line L.[2]
Differentiate \(f (x)\) .[2]
Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
State the equation of the axis of symmetry of P.[1]
Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)[3 marks]
\(x = 1.5\) (A1)[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)[3 marks]
Question
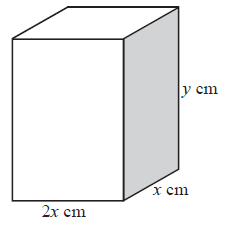
A closed rectangular box has a height \(y{\text{ cm}}\) and width \(x{\text{ cm}}\). Its length is twice its width. It has a fixed outer surface area of \(300{\text{ c}}{{\text{m}}^2}\) .
Factorise \(3{x^2} + 13x – 10\).[2]
Solve the equation \(3{x^2} + 13x – 10 = 0\).[2]
Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Find the equation of the axis of symmetry on the graph of this function.[2]
Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Calculate the minimum value of this function.[2]
Show that \(4{x^2} + 6xy = 300\).[2]
Find an expression for \(y\) in terms of \(x\).[2]
Hence show that the volume \(V\) of the box is given by \(V = 100x – \frac{4}{3}{x^3}\).[2]
Find \(\frac{{{\text{d}}V}}{{{\text{d}}x}}\).[2]
(i) Hence find the value of \(x\) and of \(y\) required to make the volume of the box a maximum.
(ii) Calculate the maximum volume.[5]
Answer/Explanation
Markscheme
\((3x – 2)(x + 5)\) (A1)(A1)[2 marks]
\((3x – 2)(x + 5) = 0\)
\(x = \frac{2}{3}\) or \(x = – 5\) (A1)(ft)(A1)(ft)(G2)[2 marks]
\(x = \frac{{ – 13}}{6}{\text{ }}( – 2.17)\) (A1)(A1)(ft)(G2)
Note: (A1) is for \(x = \), (A1) for value. (ft) if value is half way between roots in (b).[2 marks]
Minimum \(y = 3{\left( {\frac{{ – 13}}{6}} \right)^2} + 13\left( {\frac{{ – 13}}{6}} \right) – 10\) (M1)
Note: (M1) for substituting their value of \(x\) from (c) into \(f(x)\) .
\( = – 24.1\) (A1)(ft)(G2)[2 marks]
\({\text{Area}} = 2(2x)x + 2xy + 2(2x)y\) (M1)(A1)
Note: (M1) for using the correct surface area formula (which can be implied if numbers in the correct place). (A1) for using correct numbers.
\(300 = 4{x^2} + 6xy\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(6xy = 300 – 4{x^2}\) (M1)
\(y = \frac{{300 – 4{x^2}}}{{6x}}\) or \(\frac{{150 – 2{x^2}}}{{3x}}\) (A1)[2 marks]
\({\text{Volume}} = x(2x)y\) (M1)
\(V = 2{x^2}\left( {\frac{{300 – 4{x^2}}}{{6x}}} \right)\) (A1)(ft)
\( = 100x – \frac{4}{3}{x^3}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[2 marks]
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 100 – \frac{{12{x^2}}}{3}\) or \(100 – 4{x^2}\) (A1)(A1)
Note: (A1) for each term.[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column
(i) For maximum \(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) or \(100 – 4{x^2} = 0\) (M1)
\(x = 5\) (A1)(ft)
\(y = \frac{{300 – 4{{(5)}^2}}}{{6(5)}}\) or \(\left( {\frac{{150 – 2{{(5)}^2}}}{{3(5)}}} \right)\) (M1)
\( = \frac{{20}}{3}\) (A1)(ft)
(UP) (ii) \(333\frac{1}{3}{\text{ c}}{{\text{m}}^3}{\text{ }}(333{\text{ c}}{{\text{m}}^3})\)
Note: (ft) from their (e)(i) if working for volume is seen.[5 marks]
Question
Sketch the graph of y = 2x for \( – 2 \leqslant x \leqslant 3\). Indicate clearly where the curve intersects the y-axis.[3]
Write down the equation of the asymptote of the graph of y = 2x.[2]
On the same axes sketch the graph of y = 3 + 2x − x2. Indicate clearly where this curve intersects the x and y axes.[3]
Using your graphic display calculator, solve the equation 3 + 2x − x2 = 2x.[2]
Write down the maximum value of the function f (x) = 3 + 2x − x2.[1]
Use Differential Calculus to verify that your answer to (e) is correct.[5]
The curve y = px2 + qx − 4 passes through the point (2, –10).
Use the above information to write down an equation in p and q.[2]
The gradient of the curve \(y = p{x^2} + qx – 4\) at the point (2, –10) is 1.
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\).[2]
The gradient of the curve \(y = p{x^2} + qx – 4\) at the point (2, –10) is 1.
Hence, find a second equation in p and q.[1]
The gradient of the curve \(y = p{x^2} + qx – 4\) at the point (2, –10) is 1.
Solve the equations to find the value of p and of q.[3]
Answer/Explanation
Markscheme
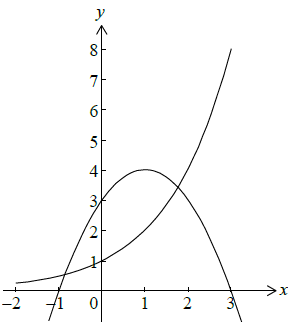(A1)(A1)(A1)
Note: Award (A1) for correct domain, (A1) for smooth curve, (A1) for y-intercept clearly indicated.[3 marks]
y = 0 (A1)(A1)
Note: Award (A1) for y = constant, (A1) for 0.[2 marks]
Note: Award (A1) for smooth parabola,
(A1) for vertex (maximum) in correct quadrant.
(A1) for all clearly indicated intercepts x = −1, x = 3 and y = 3.
The final mark is to be applied very strictly. (A1)(A1)(A1)[3 marks]
x = −0.857 x = 1.77 (G1)(G1)
Note: Award a maximum of (G1) if x and y coordinates are both given.[2 marks]
4 (G1)
Note: Award (G0) for (1, 4).[1 mark]
\(f'(x) = 2 – 2x\) (A1)(A1)
Note: Award (A1) for each correct term.
Award at most (A1)(A0) if any extra terms seen.
\(2 – 2x = 0\) (M1)
Note: Award (M1) for equating their gradient function to zero.
\(x = 1\) (A1)(ft)
\(f (1) = 3 + 2(1) – (1)^2 = 4\) (A1)
Note: The final (A1) is for substitution of x = 1 into \(f (x)\) and subsequent correct answer. Working must be seen for final (A1) to be awarded.[5 marks]
22 × p + 2q − 4 = −10 (M1)
Note: Award (M1) for correct substitution in the equation.
4p + 2q = −6 or 2p + q = −3 (A1)
Note: Accept equivalent simplified forms.[2 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 2px + q\) (A1)(A1)
Note: Award (A1) for each correct term.
Award at most (A1)(A0) if any extra terms seen.[2 marks]
4p + q = 1 (A1)(ft)[1 mark]
4p + 2q = −6
4p + q = 1 (M1)
Note: Award (M1) for sensible attempt to solve the equations.
p = 2, q = −7 (A1)(A1)(ft)(G3)[3 marks]
Question
The diagram shows an aerial view of a bicycle track. The track can be modelled by the quadratic function
\(y = \frac{{ – {x^2}}}{{10}} + \frac{{27}}{2}x\), where \(x \geqslant 0,{\text{ }}y \geqslant 0\)
(x , y) are the coordinates of a point x metres east and y metres north of O , where O is the origin (0, 0) . B is a point on the bicycle track with coordinates (100, 350) .
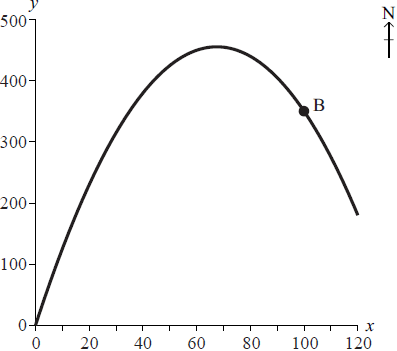
The coordinates of point A are (75, 450). Determine whether point A is on the bicycle track. Give a reason for your answer.[3]
Find the derivative of \(y = \frac{{ – {x^2}}}{{10}} + \frac{{27}}{2}x\).[2]
Use the answer in part (b) to determine if A (75, 450) is the point furthest north on the track between O and B. Give a reason for your answer.[4]
(i) Write down the midpoint of the line segment OB.
(ii) Find the gradient of the line segment OB.[3]
Scott starts from a point C(0,150) . He hikes along a straight road towards the bicycle track, parallel to the line segment OB.
Find the equation of Scott’s road. Express your answer in the form \(ax + by = c\), where \(a, b {\text{ and }} c \in \mathbb{R}\).[3]
Use your graphic display calculator to find the coordinates of the point where Scott first crosses the bicycle track.[2]
Answer/Explanation
Markscheme
\(y = – \frac{{{{75}^2}}}{{10}} + \frac{{27}}{2} \times 75\) (M1)
Note: Award (M1) for substitution of 75 in the formula of the function.
= 450 (A1)
Yes, point A is on the bike track. (A1)
Note: Do not award the final (A1) if correct working is not seen.
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{2x}}{{10}} + \frac{{27}}{2}\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 0.2x + 13.5} \right)\) (A1)(A1)
Notes: Award (A1) for each correct term. If extra terms are seen award at most (A1)(A0). Accept equivalent forms.
\( – \frac{{2x}}{{10}} + \frac{{27}}{2} = 0\) (M1)
Note: Award (M1) for equating their derivative from part (b) to zero.
\(x = 67.5\) (A1)(ft)
Note: Follow through from their derivative from part (b).
\( {\text{(Their) }} 67.5 \ne 75\) (R1)
Note: Award (R1) for a comparison of their 67.5 with 75. Comparison may be implied (eg 67.5 is the x-coordinate of the furthest north point).
OR
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – \frac{{2 \times (75)}}{{10}} + \frac{{27}}{2}\) (M1)
Note: Award (M1) for substitution of 75 into their derivative from part (b).
\(= -1.5\) (A1)(ft)
Note: Follow through from their derivative from part (b).
\({\text{(Their)}} -1.5 \ne 0\) (R1)
Note: Award (R1) for a comparison of their –1.5 with 0. Comparison may be implied (eg The gradient of the parabola at the furthest north point (vertex) is 0).
Hence A is not the furthest north point. (A1)(ft)
Note: Do not award (R0)(A1)(ft). Follow through from their derivative from part (b).
(i) M(50,175) (A1)
Note: If parentheses are omitted award (A0). Accept x = 50, y = 175.
(ii) \(\frac{{350 – 0}}{{100 – 0}}\) (M1)
Note: Award (M1) for correct substitution in gradient formula.
\( = 3.5\left( {\frac{{350}}{{100}},\frac{7}{2}} \right)\) (A1)(ft)(G2)
Note: Follow through from (d)(i) if midpoint is used to calculate gradient. Award (G1)(G0) for answer 3.5x without working.
\(y = 3.5x + 150\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for using their gradient from part (d), (A1)(ft) for correct equation of line.
\(3.5x – y = -150\) or \(7x – 2y = -300\) (or equivalent) (A1)(ft)
Note: Award (A1)(ft) for expressing their equation in the form \(ax + by = c\).
(18.4, 214) (18.3772…, 214.320…) (A1)(ft)(A1)(ft)(G2)(ft)
Notes: Follow through from their equation in (e). Coordinates must be positive for follow through marks to be awarded. If parentheses are omitted and not already penalized in (d)(i) award at most (A0)(A1)(ft). If coordinates of the two intersection points are given award (A0)(A1)(ft). Accept x = 18.4, y = 214.
Question
The front view of the edge of a water tank is drawn on a set of axes shown below.
The edge is modelled by \(y = a{x^2} + c\).
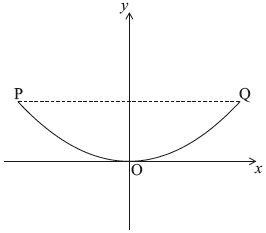
Point \({\text{P}}\) has coordinates \((-3, 1.8)\), point \({\text{O}}\) has coordinates \((0, 0)\) and point \({\text{Q}}\) has coordinates \((3, 1.8)\).
Write down the value of \(c\).[1]
Find the value of \(a\).[2]
Hence write down the equation of the quadratic function which models the edge of the water tank.[1]
The water tank is shown below. It is partially filled with water.
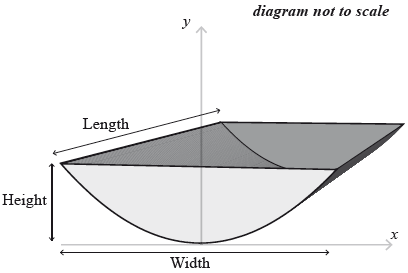
Calculate the value of y when \(x = 2.4{\text{ m}}\).[2]
The water tank is shown below. It is partially filled with water.
State what the value of \(x\) and the value of \(y\) represent for this water tank.[2]
The water tank is shown below. It is partially filled with water.
Find the value of \(x\) when the height of water in the tank is \(0.9\) m.[2]
The water tank is shown below. It is partially filled with water.
The water tank has a length of 5 m.
When the water tank is filled to a height of \(0.9\) m, the front cross-sectional area of the water is \({\text{2.55 }}{{\text{m}}^2}\).
(i) Calculate the volume of water in the tank.
The total volume of the tank is \({\text{36 }}{{\text{m}}^3}\).
(ii) Calculate the percentage of water in the tank.[2]
Answer/Explanation
Markscheme
\(0\) (A1)(G1)[1 mark]
\(1.8 = a{(3)^2} + 0\) (M1)
OR
\(1.8 = a{( – 3)^2} + 0\) (M1)
Note: Award (M1) for substitution of \(y = 1.8\) or \(x = 3\) and their value of \(c\) into equation. \(0\) may be implied.
\(a = 0.2\) \(\left( {\frac{1}{5}} \right)\) (A1)(ft)(G1)
Note: Follow through from their answer to part (a).
Award (G1) for a correct answer only.[2 marks]
\(y = 0.2{x^2}\) (A1)(ft)
Note: Follow through from their answers to parts (a) and (b).
Answer must be an equation.[1 mark]
\(0.2 \times {(2.4)^2}\) (M1)
\( = 1.15{\text{ (m)}}\) \((1.152)\) (A1)(ft)(G1)
Notes: Award (M1) for correctly substituted formula, (A1) for correct answer. Follow through from their answer to part (c).
Award (G1) for a correct answer only.[2 marks]
\(y\) is the height (A1)
positive value of \(x\) is half the width (or equivalent) (A1)[2 marks]
\(0.9 = 0.2{x^2}\) (M1)
Note: Award (M1) for setting their equation equal to \(0.9\).
\(x = \pm 2.12{\text{ (m)}}\) \(\left( { \pm \frac{3}{2}\sqrt 2 ,{\text{ }} \pm \sqrt {4.5} ,{\text{ }} \pm {\text{2.12132}} \ldots } \right)\) (A1)(ft)(G1)
Note: Accept \(2.12\). Award (G1) for a correct answer only.[2 marks]
(i) \(2.55 \times 5\) (M1)
Note: Award (M1) for correct substitution in formula.
\( = 12.8{\text{ (}}{{\text{m}}^3}{\text{)}}\) \(\left( {{\text{12.75 (}}{{\text{m}}^3}{\text{)}}} \right)\) (A1)(G2)[2 marks]
(ii) \(\frac{{12.75}}{{36}} \times 100\) (M1)
Note: Award (M1) for correct quotient multiplied by \(100\).
\( = 35.4 (\%)\) \((35.4166 \ldots )\) (A1)(ft)(G2)
Note: Award (G2) for \(35.6 (\%) (35.5555… (\%))\).
Follow through from their answer to part (g)(i).[2 marks]
Question
A distress flare is fired into the air from a ship at sea. The height, \(h\) , in metres, of the flare above sea level is modelled by the quadratic function
\[h\,(t) = – 0.2{t^2} + 16t + 12\,,\,t \geqslant 0\,,\]
where \(t\) is the time, in seconds, and \(t = 0\,\) at the moment the flare was fired.
Write down the height from which the flare was fired.[1]
Find the height of the flare \(15\) seconds after it was fired.[2]
The flare fell into the sea \(k\) seconds after it was fired.
Find the value of \(k\) .[2]
Find \(h’\,(t)\,.\)[2]
i) Show that the flare reached its maximum height \(40\) seconds after being fired.
ii) Calculate the maximum height reached by the flare.[3]
The nearest coastguard can see the flare when its height is more than \(40\) metres above sea level.
Determine the total length of time the flare can be seen by the coastguard.[3]
Answer/Explanation
Markscheme
\(12\,({\text{m}})\) (A1)
\((h\,(15) = ) – 0.2 \times {15^2} + 16 \times 15 + 12\) (M1)
Note: Award (M1) for substitution of \(15\) in expression for \(h\).
\( = 207\,({\text{m}})\) (A1)(G2)
\(h\,(k) = 0\) (M1)
Note: Award (M1) for setting \(h\) to zero.
\((k = )\,\,\,80.7\,({\text{s}})\,\,\,(80.7430)\) (A1)(G2)
Note: Award at most (M1)(A0) for an answer including \(K = – 0.743\) .
Award (A0) for an answer of \(80\) without working.
\(h’\,(t) = – 0.4t + 16\) (A1)(A1)
Note: Award (A1) for \( – 0.4t\), (A1) for \(16\). Award at most (A1)(A0) if extra terms seen. Do not accept \(x\) for \(t\).
i) \( – 0.4t + 16 = 0\) (M1)
Note: Award (M1) for setting their derivative, from part (d), to zero, provided the correct conclusion is stated and consistent with their \(h’\,(t)\).
OR
\(t = \frac{{ – 16}}{{2 \times ( – 0.2)}}\) (M1)
Note: Award (M1) for correct substitution into axis of symmetry formula, provided the correct conclusion is stated.
\(t = \,\,40\,({\text{s}})\) (AG)
ii) \( – 0.2 \times {40^2} + 16 \times 40 + 12\) (M1)
Note: Award (M1) for substitution of \(40\) in expression for \(h\).
\( = 332\,({\text{m}})\) (A1)(G2)
\(h\,(t) = 40\) (M1)
Note: Award (M1) for setting \(h\) to \(40\). Accept inequality sign.
OR
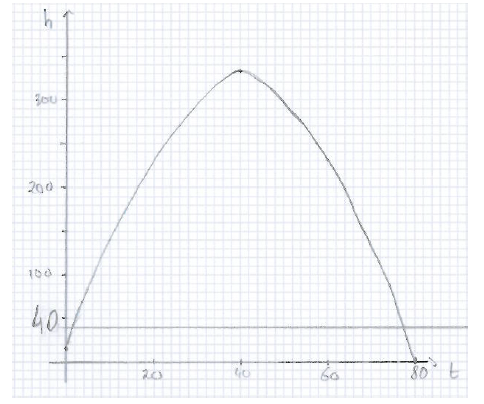
M1
Note: Award (M1) for correct sketch. Indication of scale is not required.
\(78.2 – 1.17\,\,(78.2099…\,\, – 1.79005…)\) (A1)
Note: Award (A1) for \(1.79\) and \(78.2\) seen.
(total time \( = \)) \(76.4\,({\text{s}})\,\,\,(76.4198…)\) (A1)(G2)
Note: Award (G1) if the two endpoints are given as the final answer with no working.
Question
The line \({L_1}\) has equation \(2y – x – 7 = 0\) and is shown on the diagram.
The point A has coordinates \((1,{\text{ }}4)\).
The point C has coordinates \((5,{\text{ }}12)\). M is the midpoint of AC.
The straight line, \({L_2}\), is perpendicular to AC and passes through M.
The point D is the intersection of \({L_1}\) and \({L_2}\).
The length of MD is \(\frac{{\sqrt {45} }}{2}\).
The point B is such that ABCD is a rhombus.
Show that A lies on \({L_1}\).[2]
Find the coordinates of M.[2]
Find the length of AC.[2]
Show that the equation of \({L_2}\) is \(2y + x – 19 = 0\).[5]
Find the coordinates of D.[2]
Write down the length of MD correct to five significant figures.[1]
Find the area of ABCD.[3]
Answer/Explanation
Markscheme
\(2 \times 4 – 1 – 7 = 0\) (or equivalent) (R1)
Note: For (R1) accept substitution of \(x = 1\) or \(y = 4\) into the equation followed by a confirmation that \(y = 4\) or \(x = 1\).
(since the point satisfies the equation of the line,) A lies on \({L_1}\) (A1)
Note: Do not award (A1)(R0).[2 marks]
\(\frac{{1 + 5}}{2}\) OR \(\frac{{4 + 12}}{2}\) seen (M1)
Note: Award (M1) for at least one correct substitution into the midpoint formula.
\((3,{\text{ }}8)\) (A1)(G2)
Notes: Accept \(x = 3,{\text{ }}y = 8\).
Award (M1)(A0) for \(\left( {\frac{{1 + 5}}{2},{\text{ }}\frac{{4 + 12}}{2}} \right)\).
Award (G1) for each correct coordinate seen without working.[2 marks]
\(\sqrt {{{(5 – 1)}^2} + {{(12 – 4)}^2}} \) (M1)
Note: Award (M1) for a correct substitution into distance between two points formula.
\( = 8.94{\text{ }}\left( {4\sqrt 5 ,{\text{ }}\sqrt {80} ,{\text{ }}8.94427 \ldots } \right)\) (A1)(G2)[2 marks]
gradient of \({\text{AC}} = \frac{{12 – 4}}{{5 – 1}}\) (M1)
Note: Award (M1) for correct substitution into gradient formula.
\( = 2\) (A1)
Note: Award (M1)(A1) for gradient of \({\text{AC}} = 2\) with or without working
gradient of the normal \( = – \frac{1}{2}\) (M1)
Note: Award (M1) for the negative reciprocal of their gradient of AC.
\(y – 8 = – \frac{1}{2}(x – 3)\) OR \(8 = – \frac{1}{2}(3) + c\) (M1)
Note: Award (M1) for substitution of their point and gradient into straight line formula. This (M1) can only be awarded where \( – \frac{1}{2}\) (gradient) is correctly determined as the gradient of the normal to AC.
\(2y – 16 = – (x – 3)\) OR \( – 2y + 16 = x – 3\) OR \(2y = – x + 19\) (A1)
Note: Award (A1) for correctly removing fractions, but only if their equation is equivalent to the given equation.
\(2y + x – 19 = 0\) (AG)
Note: The conclusion \(2y + x – 19 = 0\) must be seen for the (A1) to be awarded.
Where the candidate has shown the gradient of the normal to \({\text{AC}} = – 0.5\), award (M1) for \(2(8) + 3 – 19 = 0\) and (A1) for (therefore) \(2y + x – 19 = 0\).
Simply substituting \((3,{\text{ }}8)\) into the equation of \({L_2}\) with no other prior working, earns no marks.[5 marks]
\((6,{\text{ }}6.5)\) (A1)(A1)(G2)
Note: Award (A1) for 6, (A1) for 6.5. Award a maximum of (A1)(A0) if answers are not given as a coordinate pair. Accept \(x = 6,{\text{ }}y = 6.5\).
Award (M1)(A0) for an attempt to solve the two simultaneous equations \(2y – x – 7 = 0\) and \(2y + x – 19 = 0\) algebraically, leading to at least one incorrect or missing coordinate.[2 marks]
3.3541 (A1)
Note: Answer must be to 5 significant figures.[1 mark]
\(2 \times \frac{1}{2} \times \sqrt {80} \times \frac{{\sqrt {45} }}{2}\) (M1)(M1)
Notes: Award (M1) for correct substitution into area of triangle formula.
If their triangle is a quarter of the rhombus then award (M1) for multiplying their triangle by 4.
If their triangle is a half of the rhombus then award (M1) for multiplying their triangle by 2.
OR
\(\frac{1}{2} \times \sqrt {80} \times \sqrt {45} \) (M1)(M1)
Notes: Award (M1) for doubling MD to get the diagonal BD, (M1) for correct substitution into the area of a rhombus formula.
Award (M1)(M1) for \(\sqrt {80} \times \) their (f).
\( = 30\) (A1)(ft)(G3)
Notes: Follow through from parts (c) and (f).
\(8.94 \times 3.3541 = 29.9856 \ldots \)[3 marks]
Question
Consider the function \(g(x) = {x^3} + k{x^2} – 15x + 5\).
The tangent to the graph of \(y = g(x)\) at \(x = 2\) is parallel to the line \(y = 21x + 7\).
Find \(g'(x)\).[3]
Show that \(k = 6\).[2]
Find the equation of the tangent to the graph of \(y = g(x)\) at \(x = 2\). Give your answer in the form \(y = mx + c\).[3]
Use your answer to part (a) and the value of \(k\), to find the \(x\)-coordinates of the stationary points of the graph of \(y = g(x)\).[3]
Find \(g’( – 1)\).[2]
Hence justify that \(g\) is decreasing at \(x = – 1\).[1]
Find the \(y\)-coordinate of the local minimum.[2]
Answer/Explanation
Markscheme
\(3{x^2} + 2kx – 15\) (A1)(A1)(A1)
Note: Award (A1) for \(3{x^2}\), (A1) for \(2kx\) and (A1) for \( – 15\). Award at most (A1)(A1)(A0) if additional terms are seen.[3 marks]
\(21 = 3{(2)^2} + 2k(2) – 15\) (M1)(M1)
Note: Award (M1) for equating their derivative to 21. Award (M1) for substituting 2 into their derivative. The second (M1) should only be awarded if correct working leads to the final answer of \(k = 6\).
Substituting in the known value, \(k = 6\), invalidates the process; award (M0)(M0).
\(k = 6\) (AG)[2 marks]
\(g(2) = {(2)^3} + (6){(2)^2} – 15(2) + 5{\text{ }}( = 7)\) (M1)
Note: Award (M1) for substituting 2 into \(g\).
\(7 = 21(2) + c\) (M1)
Note: Award (M1) for correct substitution of 21, 2 and their 7 into gradient intercept form.
OR
\(y – 7 = 21(x – 2)\) (M1)
Note: Award (M1) for correct substitution of 21, 2 and their 7 into gradient point form.
\(y = 21x – 35\) (A1) (G2)[3 marks]
\(3{x^2} + 12x – 15 = 0\) (or equivalent) (M1)
Note: Award (M1) for equating their part (a) (with \(k = 6\) substituted) to zero.
\(x = – 5,{\text{ }}x = 1\) (A1)(ft)(A1)(ft)
Note: Follow through from part (a).[3 marks]
\(3{( – 1)^2} + 12( – 1) – 15\) (M1)
Note: Award (M1) for substituting \( – 1\) into their derivative, with \(k = 6\) substituted. Follow through from part (a).
\( = – 24\) (A1)(ft) (G2)[2 marks]
\(g’( – 1) < 0\) (therefore \(g\) is decreasing when \(x = – 1\)) (R1)[1 marks]
\(g(1) = {(1)^3} + (6){(1)^2} – 15(1) + 5\) (M1)
Note: Award (M1) for correctly substituting 6 and their 1 into \(g\).
\( = – 3\) (A1)(ft) (G2)
Note: Award, at most, (M1)(A0) or (G1) if answer is given as a coordinate pair. Follow through from part (c).[2 marks]
Question
Violeta plans to grow flowers in a rectangular plot. She places a fence to mark out the perimeter of the plot and uses 200 metres of fence. The length of the plot is \(x\) metres.
Violeta places the fence so that the area of the plot is maximized.
By selling her flowers, Violeta earns 2 Bulgarian Levs (BGN) per square metre of the plot.
Violeta wants to invest her 5000 BGN.
A bank offers a nominal annual interest rate of 4%, compounded half-yearly.
Another bank offers an interest rate of \(r\)% compounded annually, that would allow her to double her money in 12 years.
Show that the width of the plot, in metres, is given by \(100 – x\).[1]
Write down the area of the plot in terms of \(x\).[1]
Find the value of \(x\) that maximizes the area of the plot.[2]
Show that Violeta earns 5000 BGN from selling the flowers grown on the plot.[2]
Find the amount of money that Violeta would have after 6 years. Give your answer correct to two decimal places.[3]
Find how long it would take for the interest earned to be 2000 BGN.[3]
Find the lowest possible value for \(r\).[2]
Answer/Explanation
Markscheme
\(\frac{{200 – 2x}}{2}\) (or equivalent) (M1)
OR
\(2x + 2y = 200\) (or equivalent) (M1)
Note: Award (M1) for a correct expression leading to \(100 – x\) (the \(100 – x\) does not need to be seen). The 200 must be seen for the (M1) to be awarded. Do not accept \(100 – x\) substituted in the perimeter of the rectangle formula.
\(100 – x\) (AG)[1 mark]
\(({\text{area}} = ){\text{ }}x(100 – x)\)\(\,\,\,\)OR\(\,\,\,\)\( – {x^2} + 100x\) (or equivalent) (A1)[1 mark]
\(x = \frac{{ – 100}}{{ – 2}}\)\(\,\,\,\)OR\(\,\,\,\)\( – 2x + 100 = 0\)\(\,\,\,\)OR\(\,\,\,\)graphical method (M1)
Note: Award (M1) for use of axis of symmetry formula or first derivative equated to zero or a sketch graph.
\(x = 50\) (A1)(ft)(G2)
Note: Follow through from part (b), provided x is positive and less than 100.[2 marks]
\(50(100 – 50) \times 2\) (M1)(M1)
Note: Award (M1) for substituting their \(x\) into their formula for area (accept “\(50 \times 50\)” for the substituted formula), and (M1) for multiplying by 2. Award at most (M0)(M1) if their calculation does not lead to 5000 (BGN), although the 5000 (BGN) does not need to be seen explicitly.
Substitution of 50 into area formula may be seen in part (c).
5000 (BGN) (AG)[2 marks]
\(5000{\left( {1 + \frac{4}{{2 \times 100}}} \right)^{2 \times 6}}\) (M1)(A1)
Note: Award (M1) for substitution into compound interest formula, (A1) for correct substitution.
OR
\({\text{N}} = 6\)
\({\text{I}}\% = 4\)
\({\text{PV}} = – 5000\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for \({\text{C/Y}} = 2\) seen, (M1) for other correct entries.
OR
\({\text{N}} = 12\)
\({\text{I}}\% = 4\)
\({\text{PV}} = – 5000\)
\({\text{P/Y}} = 2\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for \({\text{C/Y}} = 2\) seen, (M1) for other correct entries.
6341.21 (BGN) (A1)(G3)
Note: Award (A1) for correct answer, to two decimal places only.
Award (G2) for 6341.20 or a correct, unrounded final answer if no working is seen (6341.2089…).[3 marks]
\(5000{\left( {1 + \frac{4}{{2 \times 100}}} \right)^{2 \times t}} = 7000\) (M1)(A1)(ft)
Note: Award (M1) for using the compound interest formula with a variable for time, (A1)(ft) for substituting the correct values and equating to 7000. Follow through for their “2” from part (e)(i).
OR
\({\text{I% }} = 4\)
\({\text{PV}} = ( \pm )5000\)
\({\text{FV}} = \mp 7000\)
\({\text{P/Y}} = 1\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for 7000 seen, (M1) for the other correct entries.
Award (M1) for their C/Y from part (e)(i).
OR
\({\text{I% }} = 4\)
\({\text{PV}} = ( \pm )5000\)
\({\text{FV}} = \mp 7000\)
\({\text{P/Y}} = 2\)
\({\text{C/Y}} = 2\) (M1)(A1)
Note: Award (A1) for 7000 seen, (M1) for the other correct entries.
Award (M1) for their C/Y from part (e)(i).
OR
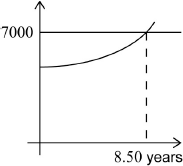(M1)(A1)(ft)
Note: Award (M1) for a sketch with a straight line intercepted by appropriate curve, (A1)(ft) for numerical answer in the range of 8.4 and 8.5.
Follow through from their part (e)(i).
\(t = 8.50{\text{ (years) }}(8.49564 \ldots )\) (A1)(ft)(G3)
Note: Award only (A1) if 16.9912… is seen without working. If working is seen, award at most (M1)(A1)(A0).[3 marks]
\(5000{\left( {1 + \frac{r}{{100}}} \right)^{12}} = 10000\) (M1)
Note: Award (M1) for correct substitution into compound interest formula with 10 000 seen.
OR
\(2 = {\left( {1 + \frac{r}{{100}}} \right)^{12}}\) (M1)
Note: Award (M1) for correct substitution and simplification of compound interest formula, equating to 2.
\(r = 5.95{\text{ (% ) }}(5.94630 \ldots )\) (A1)(G2)[2 marks]