Question
Given \(f (x) = x^2 − 3x^{−1}, x \in {\mathbb{R}}, – 5 \leqslant x \leqslant 5, x \ne 0\),
A football is kicked from a point A (a, 0), 0 < a < 10 on the ground towards a goal to the right of A.
The ball follows a path that can be modelled by part of the graph
\(y = − 0.021x^2 + 1.245x − 6.01, x \in {\mathbb{R}}, y \geqslant 0\).
x is the horizontal distance of the ball from the origin
y is the height above the ground
Both x and y are measured in metres.
Write down the equation of the vertical asymptote.[1]
Find \(f ′(x)\).[2]
Using your graphic display calculator or otherwise, write down the coordinates of any point where the graph of \(y = f (x)\) has zero gradient.[2]
Write down all intervals in the given domain for which \(f (x)\) is increasing.[3]
Using your graphic display calculator or otherwise, find the value of a.[1]
Find \(\frac{{dy}}{{dx}}\).[2]
(i) Use your answer to part (b) to calculate the horizontal distance the ball has travelled from A when its height is a maximum.
(ii) Find the maximum vertical height reached by the football.[4]
Draw a graph showing the path of the football from the point where it is kicked to the point where it hits the ground again. Use 1 cm to represent 5 m on the horizontal axis and 1 cm to represent 2 m on the vertical scale.[4]
The goal posts are 35 m from the point where the ball is kicked.
At what height does the ball pass over the goal posts?[2]
Answer/Explanation
Markscheme
equation of asymptote is x = 0 (A1)
(Must be an equation.)[1 mark]
\(f ‘(x) = 2x + 3x^{-2}\) (or equivalent) (A1) for each term (A1)(A1)[2 marks]
stationary point (–1.14, 3.93) (G1)(G1)(ft)
(-1,4) or similar error is awarded (G0)(G1)(ft). Here and also as follow through in part (d) accept exact values \( – {\left( {\frac{3}{2}} \right)^{\frac{1}{3}}}\)for the x coordinate and \(3{\left( {\frac{3}{2}} \right)^{\frac{2}{3}}}\) for the y coordinate.
OR \(2x + \frac{3}{{{x^2}}} = 0\) or equivalent
Correct coordinates as above (M1)
Follow through from candidate’s \(f ′(x)\). (A1)(ft)[2 marks]
In all alternative answers for (d), follow through from candidate’s x coordinate in part (c).
Alternative answers include:
–1.14 ≤ x < 0, 0 < x < 5 (A1)(A1)(ft)(A1)
OR [–1.14,0), (0,5)
Accept alternative bracket notation for open interval ] [. (Union of these sets is not correct, award (A2) if all else is right in this case.)
OR \( – 1.14 \leqslant x < 5,x \ne 0\)
In all versions 0 must be excluded (A1). -1.14 must be the left bound . 5 must be the right bound (A1). For \(x \geqslant – 1.14\) or \(x > – 1.14\) alone, award (A1). For \( – 1.4 \leqslant x < 0\) together with \(x > 0\) award (A2).[3 marks]
a = 5.30 (3sf) (Allow (5.30, 0) but 5.3 receives an (AP).) (A1)[1 mark]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 0.042x + 1.245\) (A1) for each term. (A1)(A1)[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) Maximum value when \(f ‘ (x) = 0\), \( – 0.042x + 1.245 = 0\), (M1)
(M1) is for either of the above but at least one must be seen.
(x = 29.6.)
Football has travelled 29.6 – 5.30 = 24.3 m (3sf) horizontally. (A1)(ft)
For answer of 24.3 m with no working or for correct subtraction of 5.3 from candidate’s x-coordinate at the maximum (if not 29.6), award (A1)(d).
(UP) (ii) Maximum vertical height, f (29.6) = 12.4 m (M1)(A1)(ft)(G2)
(M1) is for substitution into f of a value seen in part (c)(i). f(24.3) with or without evaluation is awarded (M1)(A0). For any other value without working, award (G0). If lines are seen on the graph in part (d) award (M1) and then (A1) for candidate’s value \( \pm 0.5\) (3sf not required.)[4 marks]
(not to scale)
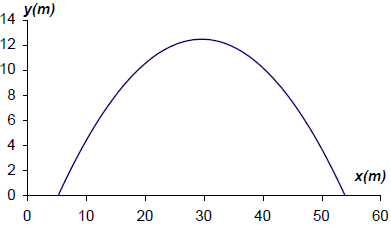(A1)(A1)(A1)(ft)(A1)(ft)
Award (A1) for labels (units not required) and scale, (A1)(ft) for max(29.6,12.4), (A1)(ft) for x-intercepts at 5.30 and 53.9, (all coordinates can be within 0.5), (A1) for well-drawn parabola ending at the x-intercepts.[4 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) f (40.3) = 10.1 m (3sf).
Follow through from (a). If graph used, award (M1) for lines drawn and (A1) for candidate’s value \( \pm 0.5\). (3sf not required). (M1)(A1)(ft)(G2)[2 marks]
Question
Consider the functions \(f(x) = \frac{{2x + 3}}{{x + 4}}\) and \(g(x) = x + 0.5\) .
Sketch the graph of the function \(f(x)\), for \( – 10 \leqslant x \leqslant 10\) . Indicating clearly the axis intercepts and any asymptotes.[6]
Write down the equation of the vertical asymptote.[2]
On the same diagram as part (a) sketch the graph of \(g(x) = x + 0.5\) .[2]
Using your graphical display calculator write down the coordinates of one of the points of intersection on the graphs of \(f\) and \(g\), giving your answer correct to five decimal places.[3]
Write down the gradient of the line \(g(x) = x + 0.5\) .[1]
The line \(L\) passes through the point with coordinates \(( – 2{\text{, }} – 3)\) and is perpendicular to the line \(g(x)\) . Find the equation of \(L\).[3]
Answer/Explanation
Markscheme
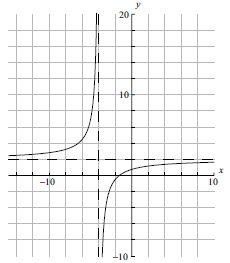(A6)
Notes: (A1) for labels and some idea of scale.
(A1) for \(x\)-intercept seen, (A1) for \(y\)-intercept seen in roughly the correct places (coordinates not required).
(A1) for vertical asymptote seen, (A1) for horizontal asymptote seen in roughly the correct places (equations of the lines not required).
(A1) for correct general shape.[6 marks]
\(x = – 4\) (A1)(A1)(ft)
Note: (A1) for \(x =\), (A1)(ft) for \( – 4\).[2 marks]
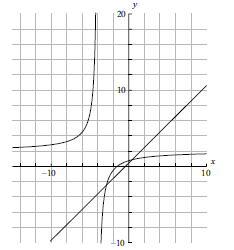(A1)(A1)
Note: (A1) for correct axis intercepts, (A1) for straight line[2 marks]
\(( – 2.85078{\text{, }} – 2.35078)\) OR \((0.35078{\text{, }}0.85078)\) (G1)(G1)(A1)(ft)
Notes: (A1) for \(x\)-coordinate, (A1) for \(y\)-coordinate, (A1)(ft) for correct accuracy. Brackets required. If brackets not used award (G1)(G0)(A1)(ft).
Accept \(x = – 2.85078\), \(y = – 2.35078\) or \(x = 0.35078\), \(y = 0.85078\).[3 marks]
\({\text{gradient}} = 1\) (A1)[1 mark]
\({\text{gradient of perpendicular}} = – 1\) (A1)(ft)
(can be implied in the next step)
\(y = mx + c\)
\( – 3 = – 1 \times – 2 + c\) (M1)
\(c = – 5\)
\(y = – x – 5\) (A1)(ft)(G2)
OR
\(y + 3 = – (x + 2)\) (M1)(A1)(ft)(G2)
Note: Award (G2) for correct answer with no working at all but (A1)(G1) if the gradient is mentioned as \( – 1\) then correct answer with no further working.[3 marks]
Question
Consider the function \(f:x \mapsto \frac{{kx}}{{{2^x}}}\).
The cost per person, in euros, when \(x\) people are invited to a party can be determined by the function
\(C(x) = x + \frac{{100}}{x}\)
Given that \(f(1) = 2\), show that \(k = 4\).[2]
Write down the values of \(q\) and \(r\) for the following table.
[2]
As \(x\) increases from \( – 1\), the graph of \(y = f(x)\) reaches a maximum value and then decreases, behaving asymptotically.
Draw the graph of \(y = f(x)\) for \( – 1 \leqslant x \leqslant 8\). Use a scale of \({\text{1 cm}}\) to represent 1 unit on both axes. The position of the maximum, \({\text{M}}\), the \(y\)-intercept and the asymptotic behaviour should be clearly shown.[4]
Using your graphic display calculator, find the coordinates of \({\text{M}}\), the maximum point on the graph of \(y = f(x)\).[2]
Write down the equation of the horizontal asymptote to the graph of \(y = f(x)\).[2]
(i) Draw and label the line \( y = 1\) on your graph.
(ii) The equation \(f(x) = 1\) has two solutions. One of the solutions is \(x = 4\). Use your graph to find the other solution.[4]
Find \(C'(x)\).[3]
Show that the cost per person is a minimum when \(10\) people are invited to the party.[2]
Calculate the minimum cost per person.[2]
Answer/Explanation
Markscheme
\(f(1) = \frac{k}{{{2^1}}}\) (M1)
Note: (M1) for substituting \(x = 1\) into the formula.
\(\frac{k}{2} = 2\) (M1)
Note: (M1) for equating to 2.
\(k = 4\) (AG)[2 marks]
\(q = 2\), \(r = 0.125\) (A1)(A1)[2 marks]
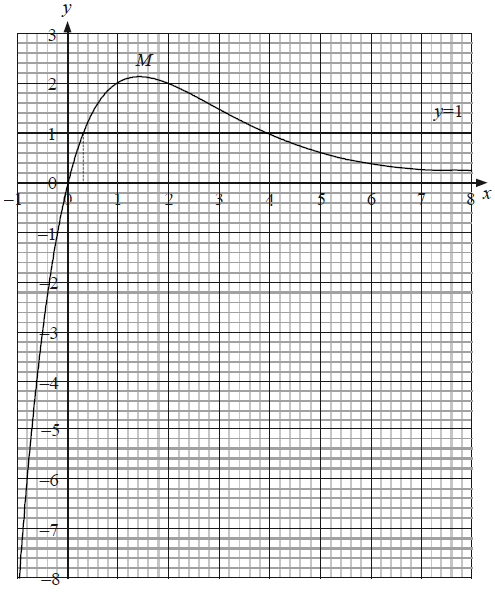(A4)
Notes: (A1) for scales and labels.
(A1) for accurate smooth curve passing through \((0, 0)\) drawn at least in the given domain.
(A1) for asymptotic behaviour (curve must not go up or cross the \(x\)-axis).
(A1) for indicating the position of the maximum point.[4 marks]
\({\text{M}}\) (\(1.44\), \(2.12\)) (G1)(G1)
Note: Brackets required, if missing award (G1)(G0). Accept \(x = 1.44\) and \(y = 2.12\).[2 marks]
\(y = 0\) (A1)(A1)
Note: (A1) for ‘\(y = \)’ provided the right hand side is a constant. (A1) for 0.[2 marks]
(i) See graph (A1)(A1)
Note: (A1) for correct line, (A1) for label.
(ii) \(x = 0.3\) (ft) from candidate’s graph. (A2)(ft)
Notes: Accept \( \pm 0.1\) from their x. For \(0.310\) award (G1)(G0). For other answers taken from the GDC and not given correct to 3 significant figures award (G0)(AP)(G0) or (G1)(G0) if (AP) already applied.[4 marks]
\(C'(x) = 1 – \frac{{100}}{{{x^2}}}\) (A1)(A1)(A1)
Note: (A1) for 1, (A1) for \( – 100\) , (A1) for \({x^2}\) as denominator or \({{x^{ – 2}}}\) as numerator. Award a maximum of (A2) if an extra term is seen.[3 marks]
For studying signs of the derivative at either side of \(x = 10\) (M1)
For saying there is a change of sign of the derivative (M1)(AG)
OR
For putting \(x = 10\) into \(C’\) and getting zero (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
OR
For solving \(C'(x) = 0\) and getting \(10\) (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
Note: For a sketch with a clear indication of the minimum or for a table with values of \(x\) at either side of \(x = 10\) award (M1)(M0).[2 marks]
\(C(10) = 10 + \frac{{100}}{{10}}\) (M1)
\(C(10) = 20\) (A1)(G2)[2 marks]
Question
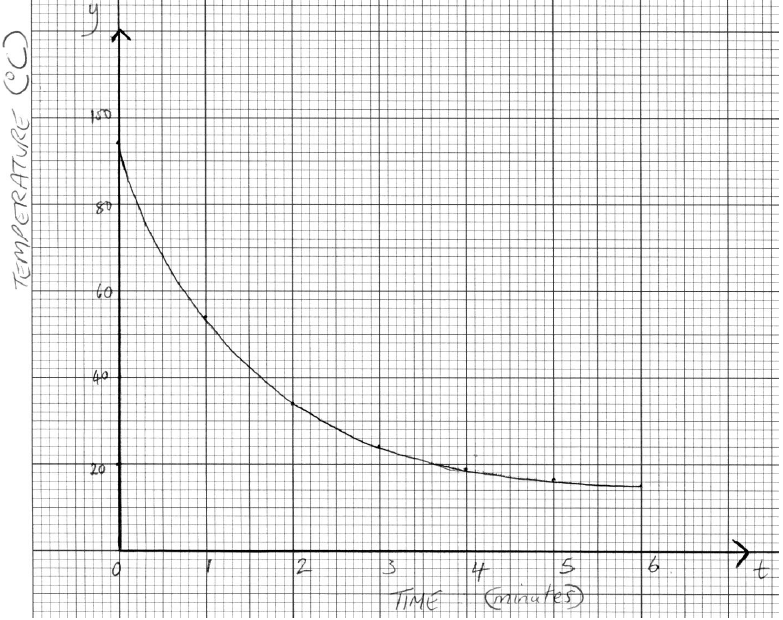
The temperature in \(^ \circ {\text{C}}\) of a pot of water removed from the cooker is given by \(T(m) = 20 + 70 \times {2.72^{ – 0.4m}}\), where \(m\) is the number of minutes after the pot is removed from the cooker.
Show that the temperature of the water when it is removed from the cooker is \({90^ \circ }{\text{C}}\).[2]
The following table shows values for \(m\) and \(T(m)\).
(i) Write down the value of \(s\).
(ii) Draw the graph of \(T(m)\) for \(0 \leqslant m \leqslant 10\) . Use a scale of \(1{\text{ cm}}\) to represent \(1\) minute on the horizontal axis and a scale of \(1{\text{ cm}}\) to represent \({10^ \circ }{\text{C}}\) on the vertical axis.
(iii) Use your graph to find how long it takes for the temperature to reach \({56^ \circ }{\text{C}}\). Show your method clearly.
(iv) Write down the temperature approached by the water after a long time. Justify your answer.[9]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
Draw the graph of \(S(m)\) on the same set of axes used for part (b).[2]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
Comment on the meaning of the constant \(20\) in the formula for \(S(m)\) in relation to the temperature of the soup.[1]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
(i) Use your graph to solve the equation \(S(m) = T(m)\) . Show your method clearly.
(ii) Hence describe by using inequalities the set of values of \(m\) for which \(S(m) > T(m)\).[4]
Answer/Explanation
Markscheme
\(T(0) = 20 + 70 \times {2.72^{ – 0.4 \times 0}} = 90\) (M1)(A1)(AG)
Note: (M1) for taking \(m = 0\) , (A1) for substituting \(0\) into the formula. For the A mark to be awarded \(90\) must be justified by correct method.[2 marks]
(i) 21.3 (A1)
(ii)
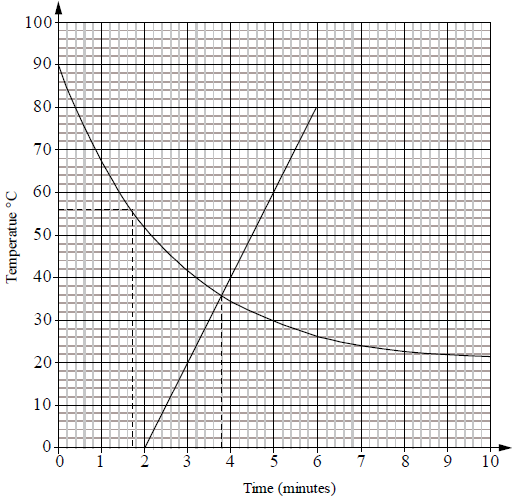(A4)(ft)
Note: Scales and labels (A1). Smooth curve (A1). All points correct including the \(y\)-intercept (A2), 1 point incorrect (A1), otherwise (A0). Follow through from their value of \(s\).
(iii) \(m = 1.7{\text{ minutes}}\) (Accept \( \pm 0.2\) ) (A2)(ft)
Note: Follow through from candidate’s graph. Accept answers in minutes and seconds if consistent with graph. If answer incorrect and correct line(s) seen on graph award (M1)(A0).
(iv) \({20^ \circ }{\text{C}}\) (A1)(ft)
The curve behaves asymptotically to the line \(y = 20\) or similar. (A1)
OR
The room temperature is 20 or similar
OR
When \({\text{m}}\) is a very large number the term \(70 \times {2.72^{ – 0.4{\text{m}}}}\) tends to zero or similar.
Note: Follow through from their graph if appropriate.[9 marks]
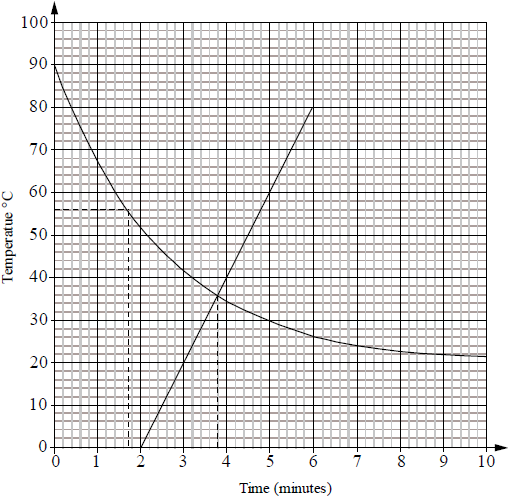(A1)(A1)
Notes: (A1) for correct line, (A1) for domain. If line not drawn on same set of axes award at most (A1)(A0).[2 marks]
It indicates by how much the temperature increases per minute. (A1)[1 mark]
(i) \(m = 3.8\) (Accept \( \pm 0.1\) ) (A2)(ft)
Note: Follow through from candidate’s graph. Accept answers in minutes and seconds if consistent with graph. If answer incorrect and correct line(s) seen on graph award (M1)(A0).
(ii) \(3.8 < m \leqslant 6\) (A1)(A1)(ft)
Note: (A1) for \(m > 3.8\) and (A1) for \(m \leqslant 6\). Follow through from candidate’s answer to part (e)(i). If candidate was already penalized in (c) for domain and does not state \(m \leqslant 6\) then award (A2)(ft).
Question
Consider the function \(f(x) = 3x + \frac{{12}}{{{x^2}}},{\text{ }}x \ne 0\).
Differentiate \(f (x)\) with respect to \(x\).[3]
Calculate \(f ′(x)\) when \(x = 1\).[2]
Use your answer to part (b) to decide whether the function, \(f\) , is increasing or decreasing at \(x = 1\). Justify your answer.[2]
Solve the equation \(f ′(x) = 0\).[3]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the coordinates of P.[2]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the gradient of T.[1]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the equation of T.[2]
Sketch the graph of the function f, for −3 ≤ x ≤ 6 and −7 ≤ y ≤ 15. Indicate clearly the point P and any intercepts of the curve with the axes.[4]
On your graph draw and label the tangent T.[2]
T intersects the graph of f at a second point. Write down the x-coordinate of this point of intersection.[1]
Answer/Explanation
Markscheme
\(f’ (x) = 3 – \frac{24}{x^3}\) (A1)(A1)(A1)
Note: Award (A1) for 3, (A1) for –24, (A1) for x3 (or x−3). If extra terms present award at most (A1)(A1)(A0).[3 marks]
\(f ‘(1) = -21\) (M1)(A1)(ft)(G2)
Note: (ft) from their derivative only if working seen.[2 marks]
Derivative (gradient, slope) is negative. Decreasing. (R1)(A1)(ft)
Note: Do not award (R0)(A1).[2 marks]
\(3 – \frac{{24}}{{{x^3}}} = 0\) (M1)
\(x^3 = 8\) (A1)
\(x = 2\) (A1)(ft)(G2)[3 marks]
(2, 9) (Accept x = 2, y = 9) (A1)(A1)(G2)
Notes: (ft) from their answer in (d).
Award (A1)(A0) if brackets not included and not previously penalized.[2 marks]
0 (A1)[1 mark]
y = 9 (A1)(A1)(ft)(G2)
Notes: Award (A1) for y = constant, (A1) for 9.
Award (A1)(ft) for their value of y in (e)(i).[2 marks]
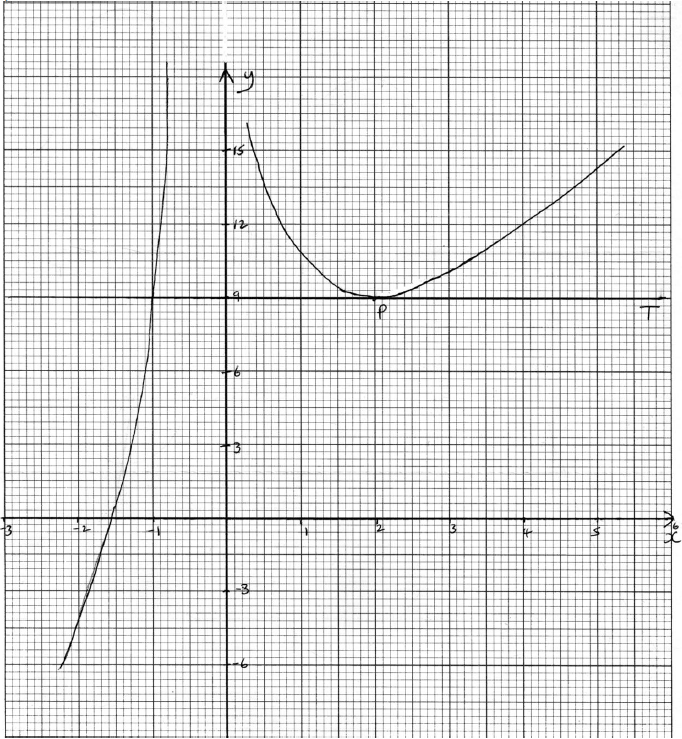(A4)
Notes: Award (A1) for labels and some indication of scale in the stated window.
Award (A1) for correct general shape (curve must be smooth and must not cross the y-axis).
Award (A1) for x-intercept seen in roughly the correct position.
Award (A1) for minimum (P).[4 marks]
Tangent drawn at P (line must be a tangent and horizontal). (A1)
Tangent labeled T. (A1)
Note: (ft) from their tangent equation only if tangent is drawn and answer is consistent with graph.[2 marks]
x = −1 (G1)(ft)[1 mark]
Question
A manufacturer claims that fertilizer has an effect on the height of rice plants. He measures the height of fertilized and unfertilized plants. The results are given in the following table.
A chi-squared test is performed to decide if the manufacturer’s claim is justified at the 1 % level of significance.
The population of fleas on a dog after t days, is modelled by
\[N = 4 \times {(2)^{\frac{t}{4}}},{\text{ }}t \geqslant 0\]
Some values of N are shown in the table below.
Write down the null and alternative hypotheses for this test.[2]
For the number of fertilized plants with height greater than 75 cm, show that the expected value is 97.5.[3]
Write down the value of \(\chi_{calc}^2\).[2]
Write down the number of degrees of freedom.[1]
Is the manufacturer’s claim justified? Give a reason for your answer.[2]
Write down the value of p.[1]
Write down the value of q.[2]
Using the values in the table above, draw the graph of N for 0 ≤ t ≤ 20. Use 1 cm to represent 2 days on the horizontal axis and 1 cm to represent 10 fleas on the vertical axis.[6]
Use your graph to estimate the number of days for the population of fleas to reach 55.[2]
Answer/Explanation
Markscheme
H0: The height of the rice plants is independent of the use of a fertilizer. (A1)
Notes: For independent accept “not associated”, can accept “the use of a fertilizer has no effect on the height of the plants”.
Do not accept “not correlated”.
H1: The height of the rice plants is not independent (dependent) of the use of fertilizer. (A1)(ft)
Note: If H0 and H1 are reversed award (A0)(A1)(ft).[2 marks]
\(\frac{{180 \times 195}}{{360}}\) or \(\frac{{180}}{{360}} \times \frac{{195}}{{360}} \times 360\) (A1)(A1)(M1)
= 97.5 (AG)
Notes: Award (A1) for numerator, (A1) for denominator (M1) for division.
If final 97.5 is not seen award at most (A1)(A0)(M1).[3 marks]
\( \chi_{calc}^2 = 14.01 (14.0, 14)\) (G2)
OR
If worked out by hand award (M1) for correct substituted formula with correct values, (A1) for correct answer. (M1)(A1)[2 marks]
2 (A1)[1 mark]
\( \chi_{calc}^2 > \chi_{crit}^2\) (R1)
The manufacturer’s claim is justified. (or equivalent statement) (A1)
Note: Do not accept (R0)(A1).[2 marks]
\(p = 4\) (G1)[1 mark]
\(q = 4(2)^{\frac{16}{4}}\) (M1)
\(= 64\) (A1)(G2)[2 marks]
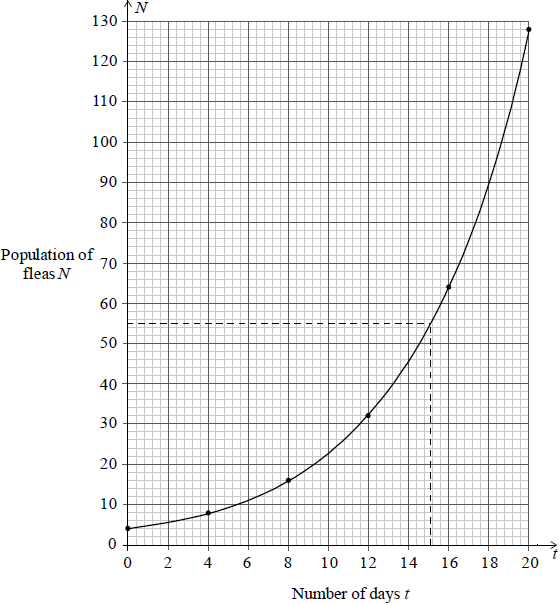(A1)(A1)(A1) (A3)
Notes: Award (A1) for x axis with correct scale and label, (A1) for y axis with correct scale and label.
Accept x and y for labels.
If x and y axis reversed award at most (A0)(A1)(ft).
(A1) for smooth curve.
Award (A3) for all 6 points correct, (A2) for 4 or 5 points correct, (A1) for 2 or 3 points correct, (A0) otherwise.[6 marks]
15 (±0.8) (M1)(A1)(ft)(G2)
Note: Award (M1) for line drawn shown on graph, (A1)(ft) from candidate’s graph.[2 marks]
Question
The diagram shows a sketch of the function f (x) = 4x3 − 9x2 − 12x + 3.
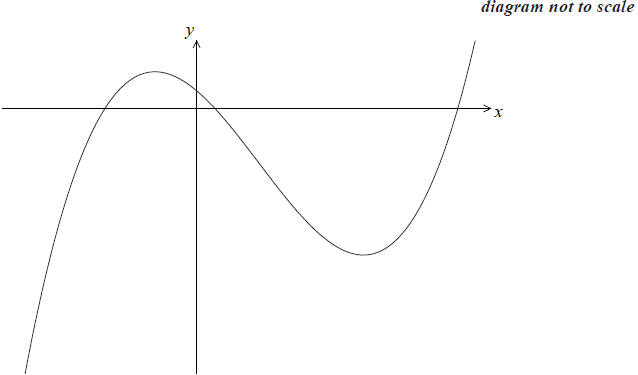
Write down the values of x where the graph of f (x) intersects the x-axis.[3]
Write down f ′(x).[3]
Find the value of the local maximum of y = f (x).[4]
Let P be the point where the graph of f (x) intersects the y axis.
Write down the coordinates of P.[1]
Let P be the point where the graph of f (x) intersects the y axis.
Find the gradient of the curve at P.[2]
The line, L, is the tangent to the graph of f (x) at P.
Find the equation of L in the form y = mx + c.[2]
There is a second point, Q, on the curve at which the tangent to f (x) is parallel to L.
Write down the gradient of the tangent at Q.[1]
There is a second point, Q, on the curve at which the tangent to f (x) is parallel to L.
Calculate the x-coordinate of Q.[3]
Answer/Explanation
Markscheme
–1.10, 0.218, 3.13 (A1)(A1)(A1)[3 marks]
f ′(x) = 12x2 – 18x – 12 (A1)(A1)(A1)
Note: Award (A1) for each correct term and award maximum of (A1)(A1) if other terms seen.[3 marks]
f ′(x) = 0 (M1)
x = –0.5, 2
x = –0.5 (A1)
Note: If x = –0.5 not stated, can be inferred from working below.
y = 4(–0.5)3 – 9(–0.5)2 – 12(–0.5) + 3 (M1)
y = 6.25 (A1)(G3)
Note: Award (M1) for their value of x substituted into f (x).
Award (M1)(G2) if sketch shown as method. If coordinate pair given then award (M1)(A1)(M1)(A0). If coordinate pair given with no working award (G2).[4 marks]
(0, 3) (A1)
Note: Accept x = 0, y = 3.[1 mark]
f ′(0) = –12 (M1)(A1)(ft)(G2)
Note: Award (M1) for substituting x = 0 into their derivative.[2 marks]
Tangent: y = –12x + 3 (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for their gradient, (A1) for intercept = 3.
Award (A1)(A0) if y = not seen.[2 marks]
–12 (A1)(ft)
Note: Follow through from their part (e).[1 mark]
12x2 – 18x – 12 = –12 (M1)
12x2 – 18x = 0 (M1)
x = 1.5, 0
At Q x = 1.5 (A1)(ft)(G2)
Note: Award (M1)(G2) for 12x2 – 18x – 12 = –12 followed by x = 1.5.
Follow through from their part (g).[3 marks]
Question
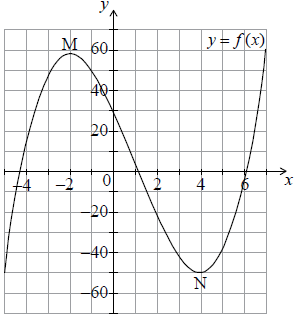
Consider the function f (x) = x3 – 3x– 24x + 30.
Write down f (0).[1]
Find \(f'(x)\).[3]
Find the gradient of the graph of f (x) at the point where x = 1.[2]
(i) Use f ‘(x) to find the x-coordinate of M and of N.
(ii) Hence or otherwise write down the coordinates of M and of N.[5]
Sketch the graph of f (x) for \( – 5 \leqslant x \leqslant 7\) and \( – 60 \leqslant y \leqslant 60\). Mark clearly M and N on your graph.[4]
Lines L1 and L2 are parallel, and they are tangents to the graph of f (x) at points A and B respectively. L1 has equation y = 21x + 111.
(i) Find the x-coordinate of A and of B.
(ii) Find the y-coordinate of B.[6]
Answer/Explanation
Markscheme
30 (A1)[1 mark]
f ‘(x) = 3x2 – 6x – 24 (A1)(A1)(A1)
Note: Award (A1) for each term. Award at most (A1)(A1) if extra terms present.[3 marks]
f ‘(1) = –27 (M1)(A1)(ft)(G2)
Note: Award (M1) for substituting x = 1 into their derivative.[2 marks]
(i) f ‘(x) = 0
3x2 – 6x – 24 = 0 (M1)
x = 4; x = –2 (A1)(ft)(A1)(ft)
Notes: Award (M1) for either f ‘(x) = 0 or 3x2 – 6x – 24 = 0 seen. Follow through from their derivative. Do not award the two answer marks if derivative not used.
(ii) M(–2, 58) accept x = –2, y = 58 (A1)(ft)
N(4, – 50) accept x = 4, y = –50 (A1)(ft)
Note: Follow through from their answer to part (d) (i).[5 marks]
(A1) for window
(A1) for a smooth curve with the correct shape
(A1) for axes intercepts in approximately the correct positions
(A1) for M and N marked on diagram and in approximately
correct position (A4)
Note: If window is not indicated award at most (A0)(A1)(A0)(A1)(ft).[4 marks]
(i) 3x2 – 6x – 24 = 21 (M1)
3x2 – 6x – 45 = 0 (M1)
x = 5; x = –3 (A1)(ft)(A1)(ft)(G3)
Note: Follow through from their derivative.
OR
Award (A1) for L1 drawn tangent to the graph of f on their sketch in approximately the correct position (x = –3), (A1) for a second tangent parallel to their L1, (A1) for x = –3, (A1) for x = 5 . (A1)(ft)(A1)(ft)(A1)(A1)
Note: If only x = –3 is shown without working award (G2). If both answers are shown irrespective of workingaward (G3).
(ii) f (5) = –40 (M1)(A1)(ft)(G2)
Notes: Award (M1) for attempting to find the image of their x = 5. Award (A1) only for (5, –40). Follow through from their x-coordinate of B only if it has been clearly identified in (f) (i).[6 marks]
Question
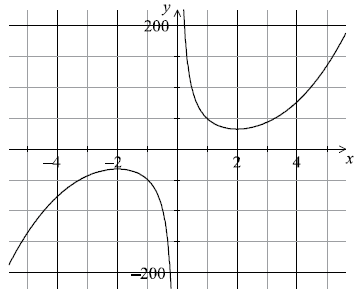
Consider the function \(f(x) = {x^3} + \frac{{48}}{x}{\text{, }}x \ne 0\).
Calculate \(f(2)\) .[2]
Sketch the graph of the function \(y = f(x)\) for \( – 5 \leqslant x \leqslant 5\) and \( – 200 \leqslant y \leqslant 200\) .[4]
Find \(f'(x)\) .[3]
Find \(f'(2)\) .[2]
Write down the coordinates of the local maximum point on the graph of \(f\) .[2]
Find the gradient of the tangent to the graph of \(f\) at \(x = 1\).[2]
There is a second point on the graph of \(f\) at which the tangent is parallel to the tangent at \(x = 1\).
Find the \(x\)-coordinate of this point.[2]
Answer/Explanation
Markscheme
\(f(2) = {2^3} + \frac{{48}}{2}\) (M1)
\(= 32\) (A1)(G2)[2 marks]
(A1) for labels and some indication of scale in an appropriate window
(A1) for correct shape of the two unconnected and smooth branches
(A1) for maximum and minimum in approximately correct positions
(A1) for asymptotic behaviour at \(y\)-axis (A4)
Notes: Please be rigorous.
The axes need not be drawn with a ruler.
The branches must be smooth: a single continuous line that does not deviate from its proper direction.
The position of the maximum and minimum points must be symmetrical about the origin.
The \(y\)-axis must be an asymptote for both branches. Neither branch should touch the axis nor must the curve approach the
asymptote then deviate away later.[4 marks]
\(f'(x) = 3{x^2} – \frac{{48}}{{{x^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(3{x^2}\) , (A1) for \( – 48\) , (A1) for \({x^{ – 2}}\) . Award a maximum of (A1)(A1)(A0) if extra terms seen.[3 marks]
\(f'(2) = 3{(2)^2} – \frac{{48}}{{{{(2)}^2}}}\) (M1)
Note: Award (M1) for substitution of \(x = 2\) into their derivative.
\(= 0\) (A1)(ft)(G1)[2 marks]
\(( – 2{\text{, }} – 32)\) or \(x = – 2\), \(y = – 32\) (G1)(G1)
Notes: Award (G0)(G0) for \(x = – 32\), \(y = – 2\) . Award at most (G0)(G1) if parentheses are omitted.[2 marks]
\(\{ y \geqslant 32\} \cup \{ y \leqslant – 32\} \) (A1)(A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) \(y \geqslant 32\) or \(y > 32\) seen, (A1)(ft) for \(y \leqslant – 32\) or \(y < – 32\) , (A1) for weak (non-strict) inequalities used in both of the above.
Accept use of \(f\) in place of \(y\). Accept alternative interval notation.
Follow through from their (a) and (e).
If domain is given award (A0)(A0)(A0).
Award (A0)(A1)(ft)(A1)(ft) for \([ – 200{\text{, }} – 32]\) , \([32{\text{, }}200]\).
Award (A0)(A1)(ft)(A1)(ft) for \(] – 200{\text{, }} – 32]\) , \([32{\text{, }}200[\).[3 marks]
\(f'(1) = – 45\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for \(f'(1)\) seen or substitution of \(x = 1\) into their derivative. Follow through from their derivative if working is seen.[2 marks]
\(x = – 1\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for equating their derivative to their \( – 45\) or for seeing parallel lines on their graph in the approximately correct position.[2 marks]
Question
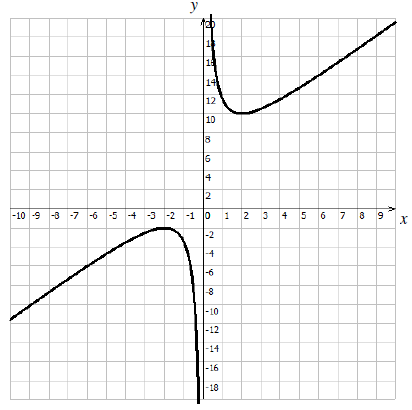
The function \(f(x)\) is defined by \(f(x) = 1.5x + 4 + \frac{6}{x}{\text{, }}x \ne 0\) .
Write down the equation of the vertical asymptote.[2]
Find \(f'(x)\) .[3]
Find the gradient of the graph of the function at \(x = – 1\).[2]
Using your answer to part (c), decide whether the function \(f(x)\) is increasing or decreasing at \(x = – 1\). Justify your answer.[2]
Sketch the graph of \(f(x)\) for \( – 10 \leqslant x \leqslant 10\) and \( – 20 \leqslant y \leqslant 20\) .[4]
\({{\text{P}}_1}\) is the local maximum point and \({{\text{P}}_2}\) is the local minimum point on the graph of \(f(x)\) .
Using your graphic display calculator, write down the coordinates of
(i) \({{\text{P}}_1}\) ;
(ii) \({{\text{P}}_2}\) .[4]
Using your sketch from (e), determine the range of the function \(f(x)\) for \( – 10 \leqslant x \leqslant 10\) .[3]
Answer/Explanation
Markscheme
\(x = 0\) (A1)(A1)
Note: Award (A1) for \(x = {\text{constant}}\), (A1) for \(0\).[2 marks]
\(f'(x) = 1.5 – \frac{6}{{{x^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(1.5\), (A1) for \( – 6\), (A1) for \({x^{ – 2}}\) . Award (A1)(A1)(A0) at most if any other term present.[3 marks]
\(1.5 – \frac{6}{{( – 1)}}\) (M1)
\( = – 4.5\) (A1)(ft)(G2)
Note: Follow through from their derivative function.[2 marks]
Decreasing, the derivative (gradient or slope) is negative (at \(x = – 1\)) (A1)(R1)(ft)
Notes: Do not award (A1)(R0). Follow through from their answer to part (c).[2 marks]
(A4)
Notes: Award (A1) for labels and some indication of scales and an appropriate window.
Award (A1) for correct shape of the two unconnected, and smooth branches.
Award (A1) for the maximum and minimum points in the approximately correct positions.
Award (A1) for correct asymptotic behaviour at \(x = 0\) .
Notes: Please be rigorous.
The axes need not be drawn with a ruler.
The branches must be smooth and single continuous lines that do not deviate from their proper direction.
The max and min points must be symmetrical about point \((0{\text{, }}4)\) .
The \(y\)-axis must be an asymptote for both branches.[4 marks]
(i) \(( – 2{\text{, }} – 2)\) or \(x = – 2\), \(y = – 2\) (G1)(G1)
(ii) \((2{\text{, }}10)\) or \(x = 2\), \(y = 10\) (G1)(G1)[4 marks]
\(\{ – 2 \geqslant y\} \) or \(\{ y \geqslant 10\} \) (A1)(A1)(ft)(A1)
Notes: (A1)(ft) for \(y > 10\) or \(y \geqslant 10\) . (A1)(ft) for \(y < – 2\) or \(y \leqslant – 2\) . (A1) for weak (non-strict) inequalities used in both of the above. Follow through from their (e) and (f).[3 marks]
Question
The diagram shows a Ferris wheel that moves with constant speed and completes a rotation every 40 seconds. The wheel has a radius of \(12\) m and its lowest point is \(2\) m above the ground.
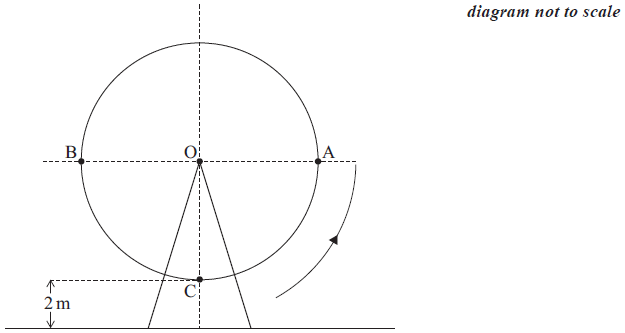
Initially, a seat C is vertically below the centre of the wheel, O. It then rotates in an anticlockwise (counterclockwise) direction.
Write down
(i) the height of O above the ground;
(ii) the maximum height above the ground reached by C .[2]
In a revolution, C reaches points A and B , which are at the same height above the ground as the centre of the wheel. Write down the number of seconds taken for C to first reach A and then B .[2]
The sketch below shows the graph of the function, \(h(t)\) , for the height above ground of C, where \(h\) is measured in metres and \(t\) is the time in seconds, \(0 \leqslant t \leqslant 40\) .
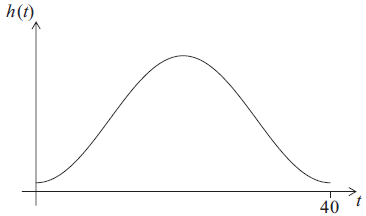
Copy the sketch and show the results of part (a) and part (b) on your diagram. Label the points clearly with their coordinates.[4]
Answer/Explanation
Markscheme
(i) \(14\) m (A1)
(ii) \(26\) m (A1)[2 marks]
A:\(10\), B:\(30\) (A1)(A1)[2 marks]
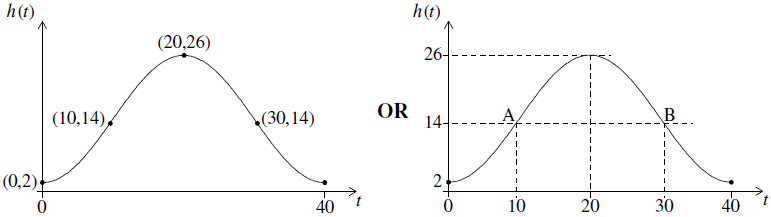(A1)(ft)(A1)(ft)(A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for coordinates of each point clearly indicated either by scale or by coordinate pairs. Points need not be labelled A and B in the second diagram. Award a maximum of (A1)(A0)(A1)(ft)(A1)(ft) if coordinates are reversed. Do not penalise reversed coordinates if this has already been penalised in Q4(a)(iii).[4 marks]
Question
Consider the function \(f(x) = – \frac{1}{3}{x^3} + \frac{5}{3}{x^2} – x – 3\).
Sketch the graph of y = f (x) for −3 ≤ x ≤ 6 and −10 ≤ y ≤ 10 showing clearly the axes intercepts and local maximum and minimum points. Use a scale of 2 cm to represent 1 unit on the x-axis, and a scale of 1 cm to represent 1 unit on the y-axis.[4]
Find the value of f (−1).[2]
Write down the coordinates of the y-intercept of the graph of f (x).[1]
Find f ‘(x).[3]
Show that \(f'( – 1) = – \frac{{16}}{3}\).[1]
Explain what f ‘(−1) represents.[2]
Find the equation of the tangent to the graph of f (x) at the point where x is –1.[2]
Sketch the tangent to the graph of f (x) at x = −1 on your diagram for (a).[2]
P and Q are points on the curve such that the tangents to the curve at these points are horizontal. The x-coordinate of P is a, and the x-coordinate of Q is b, b > a.
Write down the value of
(i) a ;
(ii) b .[2]
P and Q are points on the curve such that the tangents to the curve at these points are horizontal. The x-coordinate of P is a, and the x-coordinate of Q is b, b > a.
Describe the behaviour of f (x) for a < x < b.[1]
Answer/Explanation
Markscheme
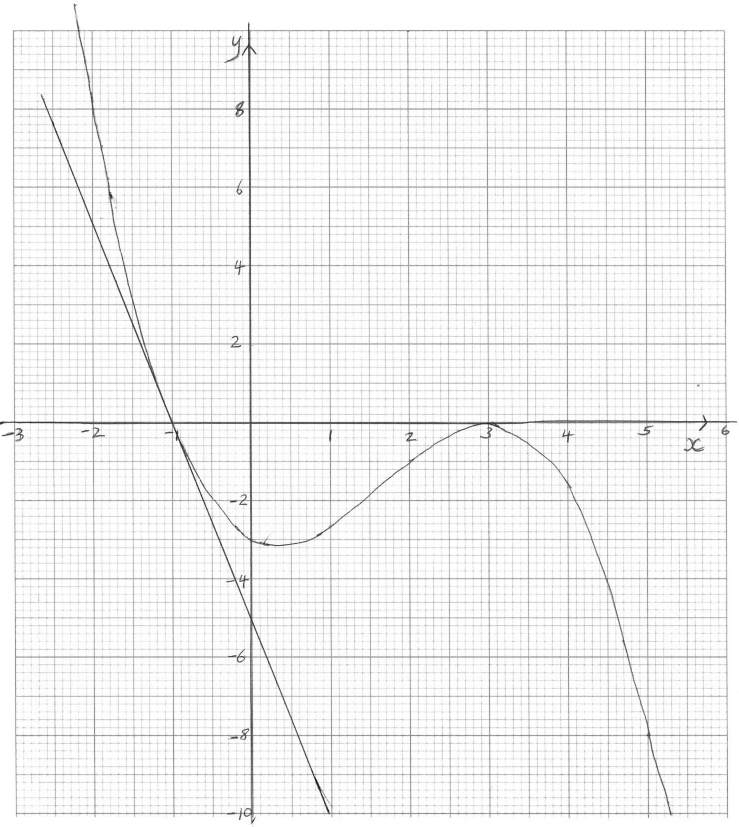
(A1) for indication of window and labels. (A1) for smooth curve that does not enter the first quadrant, the curve must consist of one line only.
(A1) for x and y intercepts in approximately correct positions (allow ±0.5).
(A1) for local maximum and minimum in approximately correct position. (minimum should be 0 ≤ x ≤ 1 and –2 ≤ y ≤ –4 ), the y-coordinate of the maximum should be 0 ± 0.5. (A4)[4 marks]
\(-\frac{1}{3}(-1)^3 + \frac{5}{3}(-1)^2 – (-1) – 3 \) (M1)
Note: Award (M1) for substitution of –1 into f (x)
= 0 (A1)(G2)[2 marks]
(0, –3) (A1)
OR
x = 0, y = –3 (A1)
Note: Award (A0) if brackets are omitted.[1 mark]
\(f'(x) = – {x^2} + \frac{{10}}{3}x – 1\) (A1)(A1)(A1)
Note: Award (A1) for each correct term. Award (A1)(A1)(A0) at most if there are extra terms.[3 marks]
\(f'( – 1) = – {( – 1)^2} + \frac{{10}}{3}( – 1) – 1\) (M1)
\(= -\frac{16}{3}\) (AG)
Note: Award (M1) for substitution of x = –1 into correct derivative only. The final answer must be seen.[1 mark]
f ‘(–1) gives the gradient of the tangent to the curve at the point with x = –1. (A1)(A1)
Note: Award (A1) for “gradient (of curve)”, (A1) for “at the point with x = –1”. Accept “the instantaneous rate of change of y” or “the (first) derivative”.[2 marks]
\(y = – \frac{16}{3} x + c\) (M1)
Note: Award (M1) for \(-\frac{16}{3}\) substituted in equation.
\(0 = – \frac{16}{3} \times (-1) + c \)
\(c = – \frac{16}{3}\)
\(y = – \frac{{16}}{3}x – \frac{{16}}{3}\) (A1)(G2)
Note: Accept y = –5.33x – 5.33.
OR
\((y – 0) = \frac{{-16}}{3}(x + 1)\) (M1)(A1)(G2)
Note: Award (M1) for \( – \frac{{16}}{3}\) substituted in equation, (A1) for correct equation. Follow through from their answer to part (b). Accept y = –5.33 (x +1). Accept equivalent equations.[2 marks]
(A1)(ft) for a tangent to their curve drawn.
(A1)(ft) for their tangent drawn at the point x = –1. (A1)(ft)(A1)(ft)
Note: Follow through from their graph. The tangent must be a straight line otherwise award at most (A0)(A1).[2 marks]
(i) \(a = \frac{1}{3}\) (G1)
(ii) \(b = 3\) (G1)
Note: If a and b are reversed award (A0)(A1).[2 marks]
f (x) is increasing (A1)[1 mark]
Question
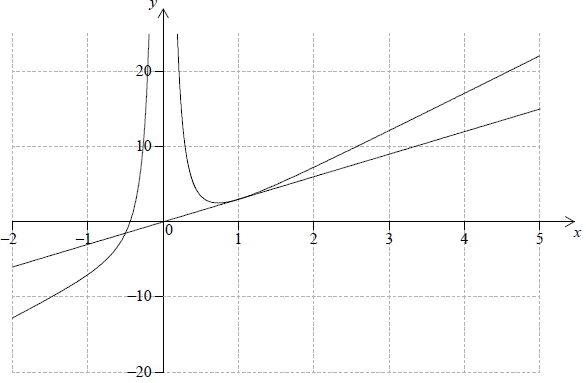
Consider the function \(g(x) = bx – 3 + \frac{1}{{{x^2}}},{\text{ }}x \ne 0\).
Write down the equation of the vertical asymptote of the graph of y = g(x) .[2]
Write down g′(x) .[3]
The line T is the tangent to the graph of y = g(x) at the point where x = 1. The gradient of T is 3.
Show that b = 5.[2]
The line T is the tangent to the graph of y = g(x) at the point where x = 1. The gradient of T is 3.
Find the equation of T.[3]
Using your graphic display calculator find the coordinates of the point where the graph of y = g(x) intersects the x-axis.[2]
(i) Sketch the graph of y = g(x) for −2 ≤ x ≤ 5 and −15 ≤ y ≤ 25, indicating clearly your answer to part (e).
(ii) Draw the line T on your sketch.[6]
Using your graphic display calculator find the coordinates of the local minimum point of y = g(x) .[2]
Write down the interval for which g(x) is increasing in the domain 0 < x < 5.[2]
Answer/Explanation
Markscheme
x = 0 (A1)(A1)
Notes: Award (A1) for x=constant, (A1) for 0. Award (A0)(A0) if answer is not an equation.[2 marks]
\(b – \frac{2}{{{x^3}}}\) (A1)(A1)(A1)
Note: Award (A1) for b, (A1) for −2, (A1) for \(\frac{1}{{{x^3}}}\) (or x−3). Award at most (A1)(A1)(A0) if extra terms seen.[3 marks]
\(3 = b – \frac{2}{{{{(1)}^3}}}\) (M1)(M1)
Note: Award (M1) for substituting 1 into their gradient function, (M1) for equating their gradient function to 3.
b = 5 (AG)
Note: Award at most (M1)(A0) if final line is not seen or b does not equal 5.[2 marks]
g(1) = 3 or (1, 3) (seen or implied from the line below) (A1)
3 = 3 × 1 + c (M1)
Note: Award (M1) for correct substitution of their point (1, 3) and gradient 3 into equation y = mx + c. Follow through from their point of tangency.
y = 3x (A1)(ft)(G2)
OR
y − 3 = 3(x − 1) (M1)(A1)(ft)(G2)
Note: Award (M1) for substitution of gradient 3 and their point (1, 3) into y − y1 = m(x − x1), (A1)(ft) for correct substitutions. Follow through from their point of tangency. Award at most (A1)(M1)(A0)(ft) if further incorrect working seen.[3 marks]
(−0.439, 0) ((−0.438785…, 0)) (G1)(G1)
Notes: If no parentheses award at most (G1)(G0). Accept x = 0.439, y = 0.[2 marks]
(i)
Award (A1) for labels and some indication of scale in the stated window.
Award (A1) for correct general shape (curve must be smooth and must not cross the y-axis)
Award (A1)(ft) for x-intercept consistent with their part (e).
Award (A1) for local minimum in the first quadrant. (A1)(A1)(A1)(ft)(A1)
(ii) Tangent to curve drawn at approximately x = 1 (A1)(A1)
Note: Award (A1) for a line tangent to curve approximately at x = 1. Must be a straight line for the mark to be awarded. Award (A1)(ft) for line passing through the origin. Follow through from their answer to part (d).[6 marks]
(0.737, 2.53) ((0.736806…, 2.52604…)) (G1)(G1)
Notes: Do not penalize for lack of parentheses if already penalized in (e). Accept x = 0.737, y = 2.53.[2 marks]
0.737 < x < 5 OR (0.737;5) (A1)(A1)(ft)
Notes: Award (A1) for correct strict or weak inequalities with x seen if the interval is given as inequalities, (A1)(ft) for 0.737 and 5 or their value from part (g).[2 marks]
Question
George leaves a cup of hot coffee to cool and measures its temperature every minute. His results are shown in the table below.
Write down the decrease in the temperature of the coffee
(i) during the first minute (between t = 0 and t =1) ;
(ii) during the second minute;
(iii) during the third minute.[3]
Assuming the pattern in the answers to part (a) continues, show that \(k = 19\).[2]
Use the seven results in the table to draw a graph that shows how the temperature of the coffee changes during the first six minutes.
Use a scale of 2 cm to represent 1 minute on the horizontal axis and 1 cm to represent 10 °C on the vertical axis.[4]
The function that models the change in temperature of the coffee is y = p (2−t )+ q.
(i) Use the values t = 0 and y = 94 to form an equation in p and q.
(ii) Use the values t =1 and y = 54 to form a second equation in p and q.[2]
Solve the equations found in part (d) to find the value of p and the value of q.[2]
The graph of this function has a horizontal asymptote.
Write down the equation of this asymptote.[2]
George decides to model the change in temperature of the coffee with a linear function using correlation and linear regression.
Use the seven results in the table to write down
(i) the correlation coefficient;
(ii) the equation of the regression line y on t.[4]
Use the equation of the regression line to estimate the temperature of the coffee at t = 3.[2]
Find the percentage error in this estimate of the temperature of the coffee at t = 3.[2]
Answer/Explanation
Markscheme
(i) 40
(ii) 20
(iii) 10 (A3)
Notes: Award (A0)(A1)(ft)(A1)(ft) for −40, −20, −10.
Award (A1)(A0)(A1)(ft) for 40, 60, 70 seen.
Award (A0)(A0)(A1)(ft) for −40, −60, −70 seen.
\(24 – k = 5\) or equivalent (A1)(M1)
Note: Award (A1) for 5 seen, (M1) for difference from 24 indicated.
\(k = 19\) (AG)
Note: If 19 is not seen award at most (A1)(M0).
(A1)(A1)(A1)(A1)
Note: Award (A1) for scales and labelled axes (t or “time” and y or “temperature”).
Accept the use of x on the horizontal axis only if “time” is also seen as the label.
Award (A2) for all seven points accurately plotted, award (A1) for 5 or 6 points accurately plotted, award (A0) for 4 points or fewer accurately plotted.
Award (A1) for smooth curve that passes through all points on domain [0, 6].
If graph paper is not used or one or more scales is missing, award a maximum of (A0)(A0)(A0)(A1).
(i) \(94 = p + q\) (A1)
(ii) \(54 = 0.5p + q\) (A1)
Note: The equations need not be simplified; accept, for example \(94 = p(2^{-0}) + q\).
p = 80, q = 14 (G1)(G1)(ft)
Note: If the equations have been incorrectly simplified, follow through even if no working is shown.
y = 14 (A1)(A1)(ft)
Note: Award (A1) for y = a constant, (A1) for their 14. Follow through from part (e) only if their q lies between 0 and 15.25 inclusive.
(i) –0.878 (–0.87787…) (G2)
Note: Award (G1) if –0.877 seen only. If negative sign omitted award a maximum of (A1)(A0).
(ii) y = –11.7t + 71.6 (y = –11.6517…t + 71.6336…) (G1)(G1)
Note: Award (G1) for –11.7t, (G1) for 71.6.
If y = is omitted award at most (G0)(G1).
If the use of x in part (c) has not been penalized (the axis has been labelled “time”) then award at most (G0)(G1).
−11.6517…(3) + 71.6339… (M1)
Note: Award (M1) for correct substitution in their part (g)(ii).
= 36.7 (36.6785…) (A1)(ft)(G2)
Note: Follow through from part (g). Accept 36.5 for use of the 3sf answers from part (g).
\(\frac{{36.6785… – 24}}{{24}} \times 100\) (M1)
Note: Award (M1) for their correct substitution in percentage error formula.
= 52.8% (52.82738…) (A1)(ft)(G2)
Note: Follow through from part (h). Accept 52.1% for use of 36.5.
Accept 52.9 % for use of 36.7. If partial working (\(\times 100\) omitted) is followed by their correct answer award (M1)(A1). If partial working is followed by an incorrect answer award (M0)(A0). The percentage sign is not required.
Question
Consider the function \(f(x) = \frac{3}{4}{x^4} – {x^3} – 9{x^2} + 20\).
Find \(f( – 2)\).[2]
Find \(f'(x)\).[3]
The graph of the function \(f(x)\) has a local minimum at the point where \(x = – 2\).
Using your answer to part (b), show that there is a second local minimum at \(x = 3\).[5]
The graph of the function \(f(x)\) has a local minimum at the point where \(x = – 2\).
Sketch the graph of the function \(f(x)\) for \( – 5 \leqslant x \leqslant 5\) and \( – 40 \leqslant y \leqslant 50\). Indicate on your
sketch the coordinates of the \(y\)-intercept.[4]
The graph of the function \(f(x)\) has a local minimum at the point where \(x = – 2\).
Write down the coordinates of the local maximum.[2]
Let \(T\) be the tangent to the graph of the function \(f(x)\) at the point \((2, –12)\).
Find the gradient of \(T\).[2]
The line \(L\) passes through the point \((2, −12)\) and is perpendicular to \(T\).
\(L\) has equation \(x + by + c = 0\), where \(b\) and \(c \in \mathbb{Z}\).
Find
(i) the gradient of \(L\);
(ii) the value of \(b\) and the value of \(c\).[5]
Answer/Explanation
Markscheme
\(\frac{3}{4}{( – 2)^4} – {( – 2)^3} – 9{( – 2)^2} + 20\) (M1)
Note: Award (M1) for substituting \(x = – 2\) in the function.
\(= 4\) (A1)(G2)
Note: If the coordinates \(( – 2,{\text{ }}4)\) are given as the answer award, at most, (M1)(A0). If no working shown award (G1).
If \(x = – 2,{\text{ }}y = 4\) seen then award full marks.[2 marks]
\(3{x^3} – 3{x^2} – 18x\) (A1)(A1)(A1)
Note: Award (A1) for each correct term, award at most (A1)(A1)(A0) if extra terms seen.[3 marks]
\(f'(3) = 3 \times {(3)^3} – 3 \times {(3)^2} – 18 \times 3\) (M1)
Note: Award (M1) for substitution in their \(f'(x)\) of \(x = 3\).
\( = 0\) (A1)
OR
\(3{x^3} – 3{x^2} – 18x = 0\) (M1)
Note: Award (M1) for equating their \(f'(x)\) to zero.
\(x = 3\) (A1)
\(f'({x_1}) = 3 \times {({x_1})^3} – 3 \times {({x_1})^2} – 18 \times {x_1} < 0\) where \(0 < {x_1} < 3\) (M1)
Note: Award (M1) for substituting a value of \({x_1}\) in the range \(0 < {x_1} < 3\) into their \(f’\) and showing it is negative (decreasing).
\(f'({x_2}) = 3 \times {({x_2})^3} – 3 \times {({x_2})^2} – 18 \times {x_2} > 0\) where \({x_2} > 3\) (M1)
Note: Award (M1) for substituting a value of \({x_2}\) in the range \({x_2} > 3\) into their \(f’\) and showing it is positive (increasing).
OR
With or without a sketch:
Showing \(f({x_1}) > f(3)\) where \({x_1} < 3\) and \({x_1}\) is close to 3. (M1)
Showing \(f({x_2}) > f(3)\) where \({x_2} > 3\) and \({x_2}\) is close to 3. (M1)
Note: If a sketch of \(f(x)\) is drawn in this part of the question and \(x = 3\) is identified as a stationary point on the curve, then
(i) award, at most, (M1)(A1)(M1)(M0) if the stationary point has been found;
(ii) award, at most, (M0)(A0)(M1)(M0) if the stationary point has not been previously found.
Since the gradients go from negative (decreasing) through zero to positive (increasing) it is a local minimum (R1)(AG)
Note: Only award (R1) if the first two marks have been awarded ie \(f'(3)\) has been shown to be equal to \(0\).[5 marks]
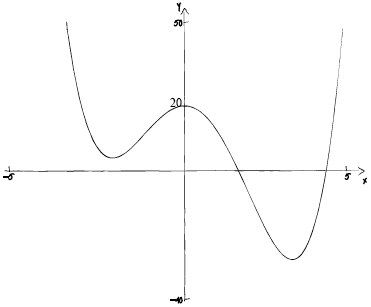(A1)(A1)(A1)(A1)
Notes: Award (A1) for labelled axes and indication of scale on both axes.
Award (A1) for smooth curve with correct shape.
Award (A1) for local minima in \({2^{{\text{nd}}}}\) and \({4^{{\text{th}}}}\) quadrants.
Award (A1) for y intercept \((0, 20)\) seen and labelled. Accept \(20\) on \(y\)–axis.
Do not award the third (A1) mark if there is a turning point on the \(x\)-axis.
If the derivative function is sketched then award, at most, (A1)(A0)(A0)(A0).
For a smooth curve (with correct shape) there should be ONE continuous thin line, no part of which is straight and no (one to many) mappings of \(x\).[4 marks]
\((0, 20)\) (G1)(G1)
Note: If parentheses are omitted award (G0)(G1).
OR
\(x = 0,{\text{ }}y = 20\) (G1)(G1)
Note: If the derivative function is sketched in part (d), award (G1)(ft)(G1)(ft) for \((–1.12, 12.2)\).[2 marks]
\(f'(2) = 3{(2)^3} – 3{(2)^2} – 18(2)\) (M1)
Notes: Award (M1) for substituting \(x = 2\) into their \(f'(x)\).
\( = – 24\) (A1)(ft)(G2)[2 marks]
(i) Gradient of perpendicular \( = \frac{1}{{24}}\) \((0.0417, 0.041666…)\) (A1)(ft)(G1)
Note: Follow through from part (f).
(ii) \(y + 12 = \frac{1}{{24}}(x – 2)\) (M1)(M1)
Note: Award (M1) for correct substitution of \((2, –12)\), (M1) for correct substitution of their perpendicular gradient into equation of line.
OR
\( – 12 = \frac{1}{{24}} \times 2 + d\) (M1)
\(d = – \frac{{145}}{{12}}\)
\(y = \frac{1}{{24}}x – \frac{{145}}{{12}}\) (M1)
Note: Award (M1) for correct substitution of \((2, –12)\) and gradient into equation of a straight line, (M1) for correct substitution of the perpendicular gradient and correct substitution of \(d\)into equation of line.
\(b = – 24,{\text{ }}c = – 290\) (A1)(ft)(A1)(ft)(G3)
Note: Follow through from parts (f) and g(i).
To award (ft) marks, \(b\) and \(c\) must be integers.
Where candidate has used \(0.042\) from g(i), award (A1)(ft) for \(–288\).[5 marks]
Question
A parcel is in the shape of a rectangular prism, as shown in the diagram. It has a length \(l\) cm, width \(w\) cm and height of \(20\) cm.
The total volume of the parcel is \(3000{\text{ c}}{{\text{m}}^3}\).
Express the volume of the parcel in terms of \(l\) and \(w\).[1]
Show that \(l = \frac{{150}}{w}\).[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
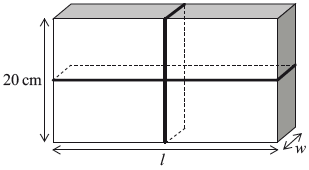
Show that the length of string, \(S\) cm, required to tie up the parcel can be written as
\[S = 40 + 4w + \frac{{300}}{w},{\text{ }}0 < w \leqslant 20.\][2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
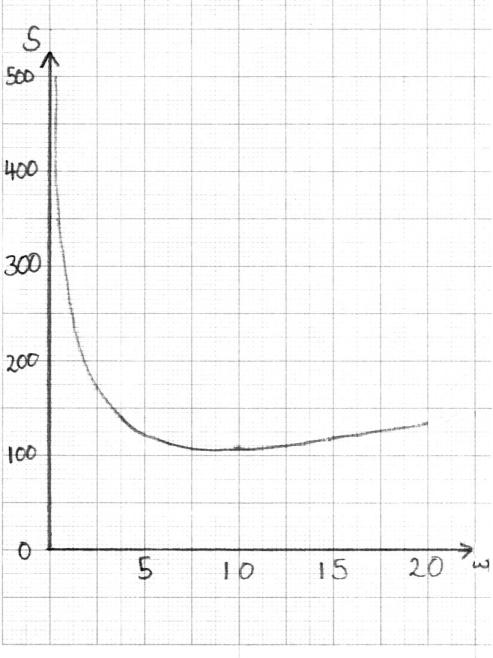
Draw the graph of \(S\) for \(0 < w \leqslant 20\) and \(0 < S \leqslant 500\), clearly showing the local minimum point. Use a scale of \(2\) cm to represent \(5\) units on the horizontal axis \(w\) (cm), and a scale of \(2\) cm to represent \(100\) units on the vertical axis \(S\) (cm).[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find \(\frac{{{\text{d}}S}}{{{\text{d}}w}}\).[3]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find the value of \(w\) for which \(S\) is a minimum.[2]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Write down the value, \(l\), of the parcel for which the length of string is a minimum.[1]
The parcel is tied up using a length of string that fits exactly around the parcel, as shown in the following diagram.
Find the minimum length of string required to tie up the parcel.[2]
Answer/Explanation
Markscheme
\(20lw\) OR \(V = 20lw\) (A1)[1 mark]
\(3000 = 20lw\) (M1)
Note: Award (M1) for equating their answer to part (a) to \(3000\).
\(l = \frac{{3000}}{{20w}}\) (M1)
Note: Award (M1) for rearranging equation to make \(l\) subject of the formula. The above equation must be seen to award (M1).
OR
\(150 = lw\) (M1)
Note: Award (M1) for division by \(20\) on both sides. The above equation must be seen to award (M1).
\(l = \frac{{150}}{w}\) (AG)[2 marks]
\(S = 2l + 4w + 2(20)\) (M1)
Note: Award (M1) for setting up a correct expression for \(S\).
\(2\left( {\frac{{150}}{w}} \right) + 4w + 2(20)\) (M1)
Notes: Award (M1) for correct substitution into the expression for \(S\). The above expression must be seen to award (M1).
\( = 40 + 4w + \frac{{300}}{w}\) (AG)[2 marks]
(A1)(A1)(A1)(A1)
Note: Award (A1) for correct scales, window and labels on axes, (A1) for approximately correct shape, (A1) for minimum point in approximately correct position, (A1) for asymptotic behaviour at \(w = 0\).
Axes must be drawn with a ruler and labeled \(w\) and \(S\).
For a smooth curve (with approximately correct shape) there should be one continuous thin line, no part of which is straight and no (one-to-many) mappings of \(w\).
The \(S\)-axis must be an asymptote. The curve must not touch the \(S\)-axis nor must the curve approach the asymptote then deviate away later.[4 marks]
\(4 – \frac{{300}}{{{w^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(4\), (A1) for \(-300\), (A1) for \(\frac{1}{{{w^2}}}\) or \({w^{ – 2}}\). If extra terms present, award at most (A1)(A1)(A0).[3 marks]
\(4 – \frac{{300}}{{{w^2}}} = 0\) OR \(\frac{{300}}{{{w^2}}} = 4\) OR \(\frac{{{\text{d}}S}}{{{\text{d}}w}} = 0\) (M1)
Note: Award (M1) for equating their derivative to zero.
\(w = 8.66{\text{ }}\left( {\sqrt {75} ,{\text{ 8.66025}} \ldots } \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (e).[2 marks]
\(17.3 \left( {\frac{{150}}{{\sqrt {75} }},{\text{ 17.3205}} \ldots } \right)\) (A1)(ft)
Note: Follow through from their answer to part (f).[1 mark]
\(40 + 4\sqrt {75} + \frac{{300}}{{\sqrt {75} }}\) (M1)
Note: Award (M1) for substitution of their answer to part (f) into the expression for \(S\).
\( = 110{\text{ (cm) }}\left( {40 + 40\sqrt 3 ,{\text{ 109.282}} \ldots } \right)\) (A1)(ft)(G2)
Note: Do not accept \(109\).
Follow through from their answers to parts (f) and (g).[2 marks]
Question
Consider the function \(f(x) = \frac{{96}}{{{x^2}}} + kx\), where \(k\) is a constant and \(x \ne 0\).
Write down \(f'(x)\).[3]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Show that \(k = 3\).[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f(2)\).[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find \(f'(2)\)[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Find the equation of the normal to the graph of \(y = f(x)\) at the point where \(x = 2\).
Give your answer in the form \(ax + by + d = 0\) where \(a,{\text{ }}b,{\text{ }}d \in \mathbb{Z}\).[3]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
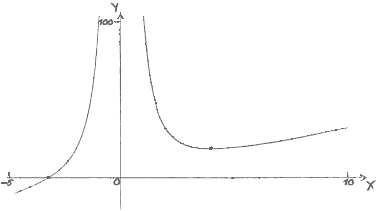
Sketch the graph of \(y = f(x)\), for \( – 5 \leqslant x \leqslant 10\) and \( – 10 \leqslant y \leqslant 100\).[4]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
Write down the coordinates of the point where the graph of \(y = f(x)\) intersects the \(x\)-axis.[2]
The graph of \(y = f(x)\) has a local minimum point at \(x = 4\).
State the values of \(x\) for which \(f(x)\) is decreasing.[2]
Answer/Explanation
Markscheme
\(\frac{{ – 192}}{{{x^3}}} + k\) (A1)(A1)(A1)
Note: Award (A1) for \(-192\), (A1) for \({x^{ – 3}}\), (A1) for \(k\) (only).
at local minimum \(f'(x) = 0\) (M1)
Note: Award (M1) for seeing \(f'(x) = 0\) (may be implicit in their working).
\(\frac{{ – 192}}{{{4^3}}} + k = 0\) (A1)
\(k = 3\) (AG)
Note: Award (A1) for substituting \(x = 4\) in their \(f'(x) = 0\), provided it leads to \(k = 3\). The conclusion \(k = 3\) must be seen for the (A1) to be awarded.
\(\frac{{96}}{{{2^2}}} + 3(2)\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in \(f(x)\).
\( = 30\) (A1)(G2)
\(\frac{{ – 192}}{{{2^3}}} + 3\) (M1)
Note: Award (M1) for substituting \(x = 2\) and \(k = 3\) in their \(f'(x)\).
\( = – 21\) (A1)(ft)(G2)
Note: Follow through from part (a).
\(y – 30 = \frac{1}{{21}}(x – 2)\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for their \(\frac{1}{{21}}\) seen, (M1) for the correct substitution of their point and their normal gradient in equation of a line.
Follow through from part (c) and part (d).
OR
gradient of normal \( = \frac{1}{{21}}\) (A1)(ft)
\(30 = \frac{1}{{21}} \times 2 + c\) (M1)
\(c = 29\frac{{19}}{{21}}\)
\(y = \frac{1}{{21}}x + 29\frac{{19}}{{21}}\;\;\;(y = 0.0476x + 29.904)\)
\(x – 21y + 628 = 0\) (A1)(ft)(G2)
Notes: Accept equivalent answers.
(A1)(A1)(A1)(A1)
Notes: Award (A1) for correct window (at least one value, other than zero, labelled on each axis), the axes must also be labelled; (A1) for a smooth curve with the correct shape (graph should not touch \(y\)-axis and should not curve away from the \(y\)-axis), on the given domain; (A1) for axis intercept in approximately the correct position (nearer \(-5\) than zero); (A1) for local minimum in approximately the correct position (first quadrant, nearer the \(y\)-axis than \(x = 10\)).
If there is no scale, award a maximum of (A0)(A1)(A0)(A1) – the final (A1) being awarded for the zero and local minimum in approximately correct positions relative to each other.
\(( – 3.17,{\text{ }}0)\;\;\;\left( {( – 3.17480 \ldots ,{\text{ 0)}}} \right)\) (G1)(G1)
Notes: If parentheses are omitted award (G0)(G1)(ft).
Accept \(x = – 3.17,{\text{ }}y = 0\). Award (G1) for \(-3.17\) seen.
\(0 < x \leqslant 4{\text{ or }}0 < x < 4\) (A1)(A1)
Notes: Award (A1) for correct end points of interval, (A1) for correct notation (note: lower inequality must be strict).
Award a maximum of (A1)(A0) if \(y\) or \(f(x)\) used in place of \(x\).
Question
Consider the function \(f(x) = 0.5{x^2} – \frac{8}{x},{\text{ }}x \ne 0\).
Find \(f( – 2)\).[2]
Find \(f'(x)\).[3]
Find the gradient of the graph of \(f\) at \(x = – 2\).[2]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
Write down the equation of \(T\).[2]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
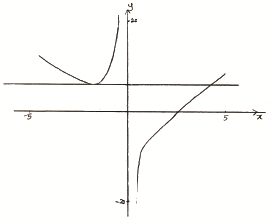
Sketch the graph of \(f\) for \( – 5 \leqslant x \leqslant 5\) and \( – 20 \leqslant y \leqslant 20\).[4]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
Draw \(T\) on your sketch.[2]
The tangent, \(T\), intersects the graph of \(f\) at a second point, P.
Use your graphic display calculator to find the coordinates of P.[2]
Answer/Explanation
Markscheme
\(0.5 \times {( – 2)^2} – \frac{8}{{ – 2}}\) (M1)
Note: Award (M1) for substitution of \(x = – 2\) into the formula of the function.
\(6\) (A1)(G2)
\(f'(x) = x + 8{x^{ – 2}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(x\), (A1) for \(8\), (A1) for \({x^{ – 2}}\) or \(\frac{1}{{{x^2}}}\) (each term must have correct sign). Award at most (A1)(A1)(A0) if there are additional terms present or further incorrect simplifications are seen.
\(f'( – 2) = – 2 + 8{( – 2)^{ – 2}}\) (M1)
Note: Award (M1) for \(x = – 2\) substituted into their \(f'(x)\) from part (b).
\( = 0\) (A1)(ft)(G2)
Note: Follow through from their derivative function.
\(y = 6\;\;\;\)OR\(\;\;\;y = 0x + 6\;\;\;\)OR\(\;\;\;y – 6 = 0(x + 2)\) (A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for their gradient from part (c), (A1)(ft) for their answer from part (a). Answer must be an equation.
Award (A0)(A0) for \(x = 6\).
(A1)(A1)(A1)(A1)
Notes: Award (A1) for labels and some indication of scales in the stated window. The point \((-2,{\text{ }}6)\) correctly labelled, or an \(x\)-value and a \(y\)-value on their axes in approximately the correct position, are acceptable indication of scales.
Award (A1) for correct general shape (curve must be smooth and must not cross the \(y\)-axis).
Award (A1) for \(x\)-intercept in approximately the correct position.
Award (A1) for local minimum in the second quadrant.
Tangent to graph drawn approximately at \(x = – 2\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for straight line tangent to curve at approximately \(x = – 2\), with approximately correct gradient. Tangent must be straight for the (A1)(ft) to be awarded.
Award (A1)(ft) for (extended) line passing through approximately their \(y\)-intercept from (d). Follow through from their gradient in part (c) and their equation in part (d).
\((4,{\text{ }}6)\;\;\;\)OR\(\;\;\;x = 4,{\text{ }}y = 6\) (G1)(ft)(G1)(ft)
Notes: Follow through from their tangent from part (d). If brackets are missing then award (G0)(G1)(ft).
If line intersects their graph at more than one point (apart from \(( – 2,{\text{ }}6)\)), follow through from the first point of intersection (to the right of \( – 2\)).
Award (G0)(G0) for \(( – 2,{\text{ }}6)\).
Question
A function, \(f\) , is given by
\[f(x) = 4 \times {2^{ – x}} + 1.5x – 5.\]
Calculate \(f(0)\)[2]
Use your graphic display calculator to solve \(f(x) = 0.\)[2]
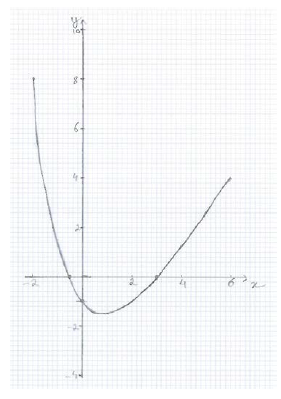
Sketch the graph of \(y = f(x)\) for \( – 2 \leqslant x \leqslant 6\) and \( – 4 \leqslant y \leqslant 10\) , showing the \(x\) and \(y\) intercepts. Use a scale of \(2\,{\text{cm}}\) to represent \(2\) units on both the horizontal axis, \(x\) , and the vertical axis, \(y\) .[4]
The function \(f\) is the derivative of a function \(g\) . It is known that \(g(1) = 3.\)
i) Calculate \(g'(1).\)
ii) Find the equation of the tangent to the graph of \(y = g(x)\) at \(x = 1.\) Give your answer in the form \(y = mx + c.\)[4]
Answer/Explanation
Markscheme
\(4 \times {2^{ – 0}} + 1.5 \times 0 – 5\) (M1)
Note: Award (M1) for substitution of \(0\) into the expression for \(f(x)\) .
\( = – 1\) (A1)(G2)
\( – 0.538\,\,\,( – 0.537670…)\) and \(3\) (A1)(A1)
Note: Award at most (A0)(A1)(ft) if answer is given as pairs of coordinates.
(A1)(A1)(A1)(ft)(A1)(ft)
Note: Award (A1) for labels and some indication of scale in the correct given window.
Award (A1) for smooth curve with correct general shape with \(f( – 2) > f(6)\) and minimum to the right of the \(y\)-axis.
Award (A1)(ft) for correct \(y\)-intercept (consistent with their part (a)).
Award (A1)(ft) for approximately correct \(x\)-intercepts (consistent with their part (b), one zero between \( – 1\) and \(0\), the other between \(2.5\) and \(3.5\)).
i) \(g'(1) = f(1) = 4 \times {2^{ – 1}} + 1.5 – 5\) (M1)
Note: Award (M1) for substitution of \(1\) into \(f(x)\).
\( = – 1.5\) (A1)(G2)
ii) \(3 = – 1.5 \times 1 + c\) OR \((y – 3) = – 1.5\,(x – 1)\) (M1)
Note: Award (M1) for correct substitution of gradient and the point \((1,\,\,3)\) into the equation of a line. Follow through from (d)(i).
\(y = – 1.5x + 4.5\) (A1)(ft)(G2)
Question
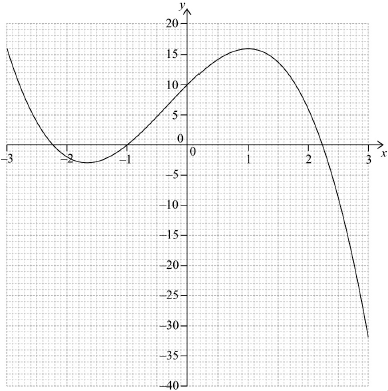
A function \(f\) is given by \(f(x) = (2x + 2)(5 – {x^2})\).
The graph of the function \(g(x) = {5^x} + 6x – 6\) intersects the graph of \(f\).
Find the exact value of each of the zeros of \(f\).[3]
Expand the expression for \(f(x)\).[1]
Find \(f’(x)\).[3]
Use your answer to part (b)(ii) to find the values of \(x\) for which \(f\) is increasing.[3]
Draw the graph of \(f\) for \( – 3 \leqslant x \leqslant 3\) and \( – 40 \leqslant y \leqslant 20\). Use a scale of 2 cm to represent 1 unit on the \(x\)-axis and 1 cm to represent 5 units on the \(y\)-axis.[4]
Write down the coordinates of the point of intersection.[2]
Answer/Explanation
Markscheme
\( – 1,{\text{ }}\sqrt 5 ,{\text{ }} – \sqrt 5 \) (A1)(A1)(A1)
Note: Award (A1) for –1 and each exact value seen. Award at most (A1)(A0)(A1) for use of 2.23606… instead of \(\sqrt 5 \).[3 marks]
\(10x – 2{x^3} + 10 – 2{x^2}\) (A1)
Notes: The expansion may be seen in part (b)(ii).[1 mark]
\(10 – 6{x^2} – 4x\) (A1)(ft)(A1)(ft)(A1)(ft)
Notes: Follow through from part (b)(i). Award (A1)(ft) for each correct term. Award at most (A1)(ft)(A1)(ft)(A0) if extra terms are seen.[3 marks]
\(10 – 6{x^2} – 4x > 0\) (M1)
Notes: Award (M1) for their \(f’(x) > 0\). Accept equality or weak inequality.
\( – 1.67 < x < 1{\text{ }}\left( { – \frac{5}{3} < x < 1,{\text{ }} – 1.66666 \ldots < x < 1} \right)\) (A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for correct endpoints, (A1)(ft) for correct weak or strict inequalities. Follow through from part (b)(ii). Do not award any marks if there is no answer in part (b)(ii).[3 marks]
(A1)(A1)(ft)(A1)(ft)(A1)
Notes: Award (A1) for correct scale; axes labelled and drawn with a ruler.
Award (A1)(ft) for their correct \(x\)-intercepts in approximately correct location.
Award (A1) for correct minimum and maximum points in approximately correct location.
Award (A1) for a smooth continuous curve with approximate correct shape. The curve should be in the given domain.
Follow through from part (a) for the \(x\)-intercepts.[4 marks]
\((1.49,{\text{ }}13.9){\text{ }}\left( {(1.48702 \ldots ,{\text{ }}13.8714 \ldots )} \right)\) (G1)(ft)(G1)(ft)
Notes: Award (G1) for 1.49 and (G1) for 13.9 written as a coordinate pair. Award at most (G0)(G1) if parentheses are missing. Accept \(x = 1.49\) and \(y = 13.9\). Follow through from part (b)(i).[2 marks]
Question
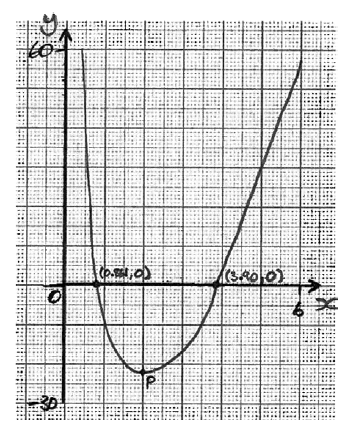
Consider the function \(f\left( x \right) = \frac{{48}}{x} + k{x^2} – 58\), where x > 0 and k is a constant.
The graph of the function passes through the point with coordinates (4 , 2).
P is the minimum point of the graph of f (x).
Find the value of k.[2]
Using your value of k , find f ′(x).[3]
Use your answer to part (b) to show that the minimum value of f(x) is −22 .[3]
Write down the two values of x which satisfy f (x) = 0.[2]
Sketch the graph of y = f (x) for 0 < x ≤ 6 and −30 ≤ y ≤ 60.
Clearly indicate the minimum point P and the x-intercepts on your graph.[4]
Answer/Explanation
Markscheme
\(\frac{{48}}{4} + k \times {4^2} – 58 = 2\) (M1)
Note: Award (M1) for correct substitution of x = 4 and y = 2 into the function.
k = 3 (A1) (G2)[2 marks]
\(\frac{{ – 48}}{{{x^2}}} + 6x\) (A1)(A1)(A1)(ft) (G3)
Note: Award (A1) for −48 , (A1) for x−2, (A1)(ft) for their 6x. Follow through from part (a). Award at most (A1)(A1)(A0) if additional terms are seen.[3 marks]
\(\frac{{ – 48}}{{{x^2}}} + 6x = 0\) (M1)
Note: Award (M1) for equating their part (b) to zero.
x = 2 (A1)(ft)
Note: Follow through from part (b). Award (M1)(A1) for \(\frac{{ – 48}}{{{{\left( 2 \right)}^2}}} + 6\left( 2 \right) = 0\) seen.
Award (M0)(A0) for x = 2 seen either from a graphical method or without working.
\(\frac{{48}}{2} + 3 \times {2^2} – 58\,\,\,\left( { = – 22} \right)\) (M1)
Note: Award (M1) for substituting their 2 into their function, but only if the final answer is −22. Substitution of the known result invalidates the process; award (M0)(A0)(M0).
−22 (AG)[3 marks]
0.861 (0.860548…), 3.90 (3.90307…) (A1)(ft)(A1)(ft) (G2)
Note: Follow through from part (a) but only if the answer is positive. Award at most (A1)(ft)(A0) if answers are given as coordinate pairs or if extra values are seen. The function f (x) only has two x-intercepts within the domain. Do not accept a negative x-intercept.[2 marks]
(A1)(A1)(ft)(A1)(ft)(A1)(ft)
Note: Award (A1) for correct window. Axes must be labelled.
(A1)(ft) for a smooth curve with correct shape and zeros in approximately correct positions relative to each other.
(A1)(ft) for point P indicated in approximately the correct position. Follow through from their x-coordinate in part (c). (A1)(ft) for two x-intercepts identified on the graph and curve reflecting asymptotic properties.[4 marks]
Question
Consider the curve y = 2x3 − 9x2 + 12x + 2, for −1 < x < 3
Sketch the curve for −1 < x < 3 and −2 < y < 12.[4]
A teacher asks her students to make some observations about the curve.
Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.
State the name of the student who made an incorrect observation.[1]
Find the value of y when x = 1 .[2]
Find \(\frac{{{\text{dy}}}}{{{\text{dx}}}}\).[3]
Show that the stationary points of the curve are at x = 1 and x = 2.[2]
Given that y = 2x3 − 9x2 + 12x + 2 = k has three solutions, find the possible values of k.[3]
Answer/Explanation
Markscheme
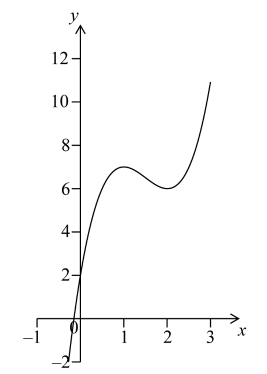(A1)(A1)(A1)(A1)
Note: Award (A1) for correct window (condone a window which is slightly off) and axes labels. An indication of window is necessary. −1 to 3 on the x-axis and −2 to 12 on the y-axis and a graph in that window.
(A1) for correct shape (curve having cubic shape and must be smooth).
(A1) for both stationary points in the 1st quadrant with approximate correct position,
(A1) for intercepts (negative x-intercept and positive y intercept) with approximate correct position.[4 marks]
Rick (A1)
Note: Award (A0) if extra names stated.[1 mark]
2(1)3 − 9(1)2 + 12(1) + 2 (M1)
Note: Award (M1) for correct substitution into equation.
= 7 (A1)(G2)[2 marks
6x2 − 18x + 12 (A1)(A1)(A1)
Note: Award (A1) for each correct term. Award at most (A1)(A1)(A0) if extra terms seen.[3 marks]
6x2 − 18x + 12 = 0 (M1)
Note: Award (M1) for equating their derivative to 0. If the derivative is not explicitly equated to 0, but a subsequent solving of their correct equation is seen, award (M1).
6(x − 1)(x − 2) = 0 (or equivalent) (M1)
Note: Award (M1) for correct factorization. The final (M1) is awarded only if answers are clearly stated.
Award (M0)(M0) for substitution of 1 and of 2 in their derivative.
x = 1, x = 2 (AG)[2 marks]
6 < k < 7 (A1)(A1)(ft)(A1)
Note: Award (A1) for an inequality with 6, award (A1)(ft) for an inequality with 7 from their part (c) provided it is greater than 6, (A1) for their correct strict inequalities. Accept ]6, 7[ or (6, 7).[3 marks]
Question
A deep sea diver notices that the intensity of light, \(I\) , below the surface of the ocean decreases with depth, \(d\) , according to the formula
\[I = k{(1.05)^{ – d}}{\text{,}}\]where \(I\) is expressed as a percentage, \(d\) is the depth in metres below the surface and \(k\) is a constant.
The intensity of light at the surface is \(100\% \).
Calculate the value of \(k\) .[2]
Find the intensity of light at a depth \(25{\text{ m}}\) below the surface.[2]
To be able to see clearly, a diver needs the intensity of light to be at least \(65\% \).
Using your graphic display calculator, find the greatest depth below the surface at which she can see clearly.[2]
The table below gives the intensity of light (correct to the nearest integer) at different depths.
Using this information draw the graph of \(I\) against \(d\) for \(0 \leqslant d \leqslant 100\) . Use a scale of \(1{\text{ cm}}\) to represent 10 metres on the horizontal axis and 1 cm to represent \(10\% \) on the vertical axis.[4]
Some sea creatures have adapted so they can see in low intensity light and cannot tolerate too much light.
Indicate clearly on your graph the range of depths sea creatures could inhabit if they can tolerate between \(5\% \) and \(35\% \) of the light intensity at the surface.[2]
Answer/Explanation
Markscheme
\(d = 0\), \(k = 100\) (M1)(A1)(G2)
Note: Award (M1) for \(d = 0\) seen.
\(I = 100 \times {(1.05)^{ – 25}} = 29.5(\% )\) (\(29.5302 \ldots \)) (M1)(A1)(ft)(G2)
\(65 = 100 \times {(1.05)^{ – d}}\) (M1)
Note: Award (M1) for sketch with line drawn at \(y = 65\) .
\(d = 8.83{\text{ (m)}}\) (\(8.82929 \ldots \)) (A1)(ft)(G2)
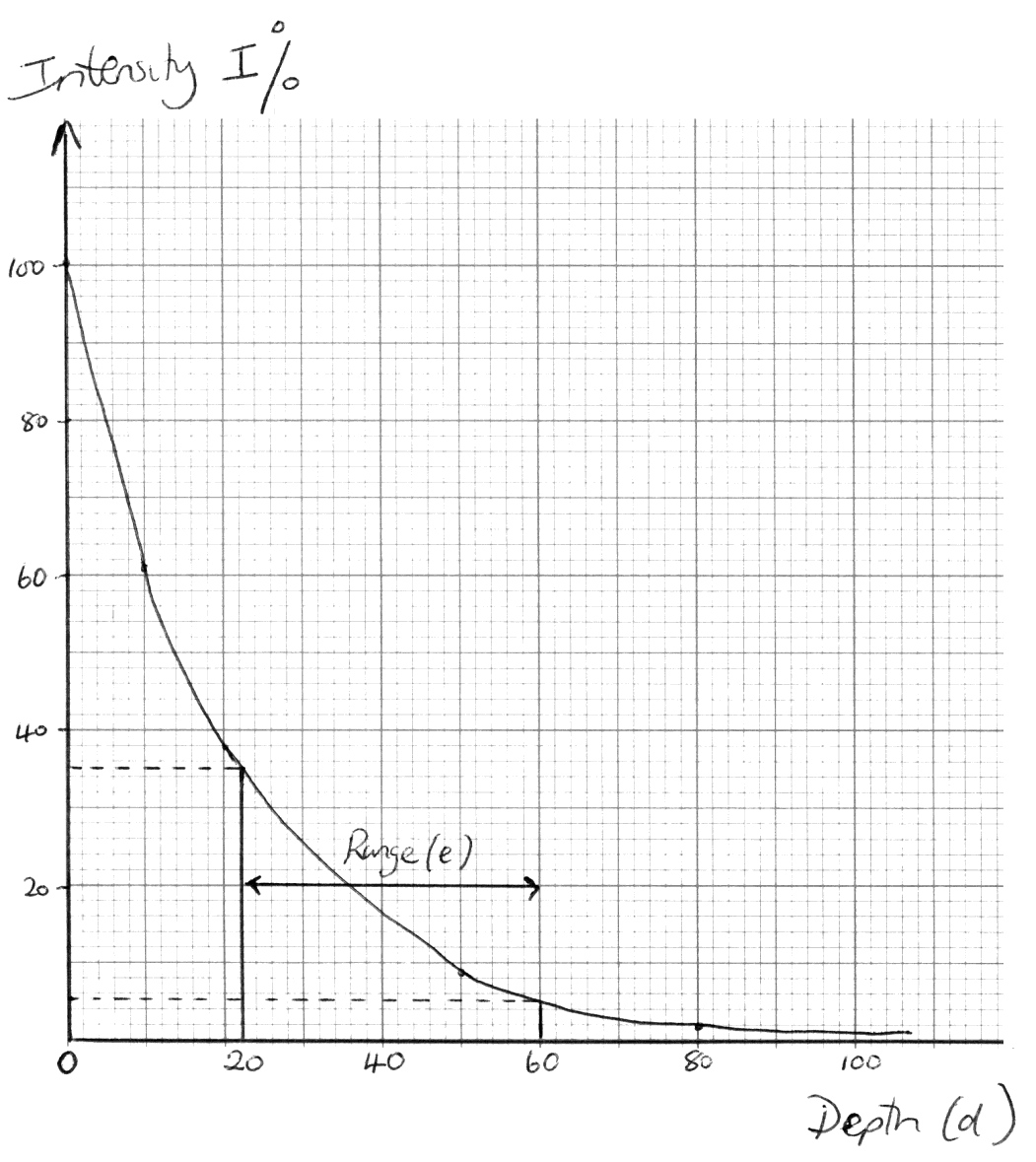
(A1) for labels and scales
(A2) for all points correct, (A1) for 3 or 4 points correct
(A1) for smooth curve asymptotic to the \(x\)-axis (A4)d.
Lines in approx correct positions on graph (M1)
The range of values indicated (arrows or shading) \(22\)–\(60{\text{ m}}\) (A1)