Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
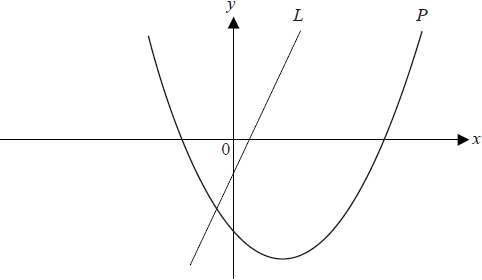
Find the gradient of the line L.[2]
Differentiate \(f (x)\) .[2]
Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
State the equation of the axis of symmetry of P.[1]
Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)[3 marks]
\(x = 1.5\) (A1)[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)[3 marks]
Question
Consider the curve \(y = {x^3} + \frac{3}{2}{x^2} – 6x – 2\) .
(i) Write down the value of \(y\) when \(x\) is \(2\).
(ii) Write down the coordinates of the point where the curve intercepts the \(y\)-axis.[3]
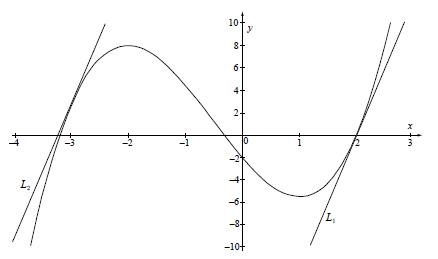
Sketch the curve for \( – 4 \leqslant x \leqslant 3\) and \( – 10 \leqslant y \leqslant 10\). Indicate clearly the information found in (a).[4]
Find \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) .[3]
Let \({L_1}\) be the tangent to the curve at \(x = 2\).
Let \({L_2}\) be a tangent to the curve, parallel to \({L_1}\).
(i) Show that the gradient of \({L_1}\) is \(12\).
(ii) Find the \(x\)-coordinate of the point at which \({L_2}\) and the curve meet.
(iii) Sketch and label \({L_1}\) and \({L_2}\) on the diagram drawn in (b).[8]
It is known that \(\frac{{{\text{d}}y}}{{{\text{d}}x}} > 0\) for \(x < – 2\) and \(x > b\) where \(b\) is positive.
(i) Using your graphic display calculator, or otherwise, find the value of \(b\).
(ii) Describe the behaviour of the curve in the interval \( – 2 < x < b\) .
(iii) Write down the equation of the tangent to the curve at \(x = – 2\).[5]
Answer/Explanation
Markscheme
(i) \(y = 0\) (A1)
(ii) \((0{\text{, }}{- 2})\) (A1)(A1)
Note: Award (A1)(A0) if brackets missing.
OR
\(x = 0{\text{, }}y = – 2\) (A1)(A1)
Note: If coordinates reversed award (A0)(A1)(ft). Two coordinates must be given.[3 marks]
(A4)
Notes: (A1) for appropriate window. Some indication of scale on the \(x\)-axis must be present (for example ticks). Labels not required. (A1) for smooth curve and shape, (A1) for maximum and minimum in approximately correct position, (A1) for \(x\) and \(y\) intercepts found in (a) in approximately correct position.[4 marks]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 3{x^2} + 3x – 6\) (A1)(A1)(A1)
Note: (A1) for each correct term. Award (A1)(A1)(A0) at most if any other term is present.[3 marks]
(i) \(3 \times 4 + 3 \times 2 – 6 = 12\) (M1)(A1)(AG)
Note: (M1) for using the derivative and substituting \(x = 2\) . (A1) for correct (and clear) substitution. The \(12\) must be seen.
(ii) Gradient of \({L_2}\) is \(12\) (can be implied) (A1)
\(3{x^2} + 3x – 6 = 12\) (M1)
\(x = – 3\) (A1)(G2)
Note: (M1) for equating the derivative to \(12\) or showing a sketch of the derivative together with a line at \(y = 12\) or a table of values showing the \(12\) in the derivative column.
(iii) (A1) for \({L_1}\) correctly drawn at approx the correct point (A1)
(A1) for \({L_2}\) correctly drawn at approx the correct point (A1)
(A1) for 2 parallel lines (A1)
Note: If lines are not labelled award at most (A1)(A1)(A0). Do not accept 2 horizontal or 2 vertical parallel lines.[8 marks]
(i) \(b = 1\) (G2)
(ii) The curve is decreasing. (A1)
Note: Accept any valid description.
(iii) \(y = 8\) (A1)(A1)(G2)
Note: (A1) for “\(y =\) a constant”, (A1) for \(8\).[5 marks]
Question
Consider the function \(f(x) = 3x + \frac{{12}}{{{x^2}}},{\text{ }}x \ne 0\).
Differentiate \(f (x)\) with respect to \(x\).[3]
Calculate \(f ′(x)\) when \(x = 1\).[2]
Use your answer to part (b) to decide whether the function, \(f\) , is increasing or decreasing at \(x = 1\). Justify your answer.[2]
Solve the equation \(f ′(x) = 0\).[3]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the coordinates of P.[2]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the gradient of T.[1]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the equation of T.[2]
Sketch the graph of the function f, for −3 ≤ x ≤ 6 and −7 ≤ y ≤ 15. Indicate clearly the point P and any intercepts of the curve with the axes.[4]
On your graph draw and label the tangent T.[2]
T intersects the graph of f at a second point. Write down the x-coordinate of this point of intersection.[1]
Answer/Explanation
Markscheme
\(f’ (x) = 3 – \frac{24}{x^3}\) (A1)(A1)(A1)
Note: Award (A1) for 3, (A1) for –24, (A1) for x3 (or x−3). If extra terms present award at most (A1)(A1)(A0).[3 marks]
\(f ‘(1) = -21\) (M1)(A1)(ft)(G2)
Note: (ft) from their derivative only if working seen.[2 marks]
Derivative (gradient, slope) is negative. Decreasing. (R1)(A1)(ft)
Note: Do not award (R0)(A1).[2 marks]
\(3 – \frac{{24}}{{{x^3}}} = 0\) (M1)
\(x^3 = 8\) (A1)
\(x = 2\) (A1)(ft)(G2)[3 marks]
(2, 9) (Accept x = 2, y = 9) (A1)(A1)(G2)
Notes: (ft) from their answer in (d).
Award (A1)(A0) if brackets not included and not previously penalized.[2 marks]
0 (A1)[1 mark]
y = 9 (A1)(A1)(ft)(G2)
Notes: Award (A1) for y = constant, (A1) for 9.
Award (A1)(ft) for their value of y in (e)(i).[2 marks]
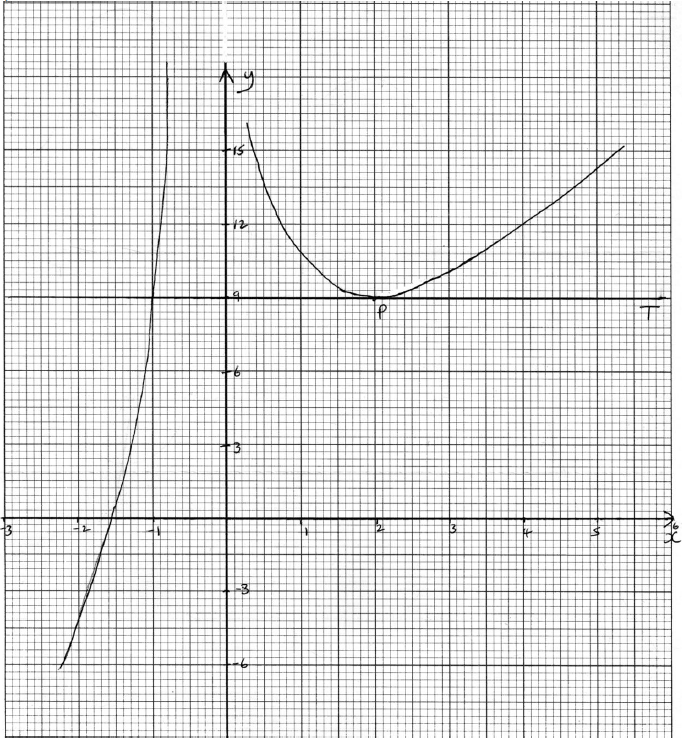(A4)
Notes: Award (A1) for labels and some indication of scale in the stated window.
Award (A1) for correct general shape (curve must be smooth and must not cross the y-axis).
Award (A1) for x-intercept seen in roughly the correct position.
Award (A1) for minimum (P).[4 marks]
Tangent drawn at P (line must be a tangent and horizontal). (A1)
Tangent labeled T. (A1)
Note: (ft) from their tangent equation only if tangent is drawn and answer is consistent with graph.[2 marks]
x = −1 (G1)(ft)[1 mark]
Question
Consider the function f (x) = x3 – 3x– 24x + 30.
Write down f (0).[1]
Find \(f'(x)\).[3]
Find the gradient of the graph of f (x) at the point where x = 1.[2]
(i) Use f ‘(x) to find the x-coordinate of M and of N.
(ii) Hence or otherwise write down the coordinates of M and of N.[5]
Sketch the graph of f (x) for \( – 5 \leqslant x \leqslant 7\) and \( – 60 \leqslant y \leqslant 60\). Mark clearly M and N on your graph.[4]
Lines L1 and L2 are parallel, and they are tangents to the graph of f (x) at points A and B respectively. L1 has equation y = 21x + 111.
(i) Find the x-coordinate of A and of B.
(ii) Find the y-coordinate of B.[6]
Answer/Explanation
Markscheme
30 (A1)[1 mark]
f ‘(x) = 3x2 – 6x – 24 (A1)(A1)(A1)
Note: Award (A1) for each term. Award at most (A1)(A1) if extra terms present.[3 marks]
f ‘(1) = –27 (M1)(A1)(ft)(G2)
Note: Award (M1) for substituting x = 1 into their derivative.[2 marks]
(i) f ‘(x) = 0
3x2 – 6x – 24 = 0 (M1)
x = 4; x = –2 (A1)(ft)(A1)(ft)
Notes: Award (M1) for either f ‘(x) = 0 or 3x2 – 6x – 24 = 0 seen. Follow through from their derivative. Do not award the two answer marks if derivative not used.
(ii) M(–2, 58) accept x = –2, y = 58 (A1)(ft)
N(4, – 50) accept x = 4, y = –50 (A1)(ft)
Note: Follow through from their answer to part (d) (i).[5 marks]
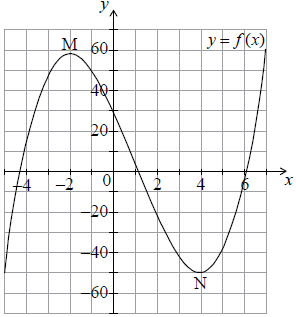
(A1) for window
(A1) for a smooth curve with the correct shape
(A1) for axes intercepts in approximately the correct positions
(A1) for M and N marked on diagram and in approximately
correct position (A4)
Note: If window is not indicated award at most (A0)(A1)(A0)(A1)(ft).[4 marks]
(i) 3x2 – 6x – 24 = 21 (M1)
3x2 – 6x – 45 = 0 (M1)
x = 5; x = –3 (A1)(ft)(A1)(ft)(G3)
Note: Follow through from their derivative.
OR
Award (A1) for L1 drawn tangent to the graph of f on their sketch in approximately the correct position (x = –3), (A1) for a second tangent parallel to their L1, (A1) for x = –3, (A1) for x = 5 . (A1)(ft)(A1)(ft)(A1)(A1)
Note: If only x = –3 is shown without working award (G2). If both answers are shown irrespective of workingaward (G3).
(ii) f (5) = –40 (M1)(A1)(ft)(G2)
Notes: Award (M1) for attempting to find the image of their x = 5. Award (A1) only for (5, –40). Follow through from their x-coordinate of B only if it has been clearly identified in (f) (i).[6 marks]
Question
Consider the function \(f(x) = {x^3} + \frac{{48}}{x}{\text{, }}x \ne 0\).
Calculate \(f(2)\) .[2]
Sketch the graph of the function \(y = f(x)\) for \( – 5 \leqslant x \leqslant 5\) and \( – 200 \leqslant y \leqslant 200\) .[4]
Find \(f'(x)\) .[3]
Find \(f'(2)\) .[2]
Write down the coordinates of the local maximum point on the graph of \(f\) .[2]
Find the gradient of the tangent to the graph of \(f\) at \(x = 1\).[2]
There is a second point on the graph of \(f\) at which the tangent is parallel to the tangent at \(x = 1\).
Find the \(x\)-coordinate of this point.[2]
Answer/Explanation
Markscheme
\(f(2) = {2^3} + \frac{{48}}{2}\) (M1)
\(= 32\) (A1)(G2)[2 marks]
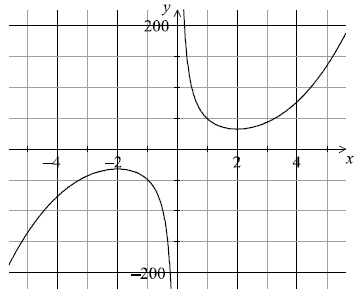
(A1) for labels and some indication of scale in an appropriate window
(A1) for correct shape of the two unconnected and smooth branches
(A1) for maximum and minimum in approximately correct positions
(A1) for asymptotic behaviour at \(y\)-axis (A4)
Notes: Please be rigorous.
The axes need not be drawn with a ruler.
The branches must be smooth: a single continuous line that does not deviate from its proper direction.
The position of the maximum and minimum points must be symmetrical about the origin.
The \(y\)-axis must be an asymptote for both branches. Neither branch should touch the axis nor must the curve approach the
asymptote then deviate away later.[4 marks]
\(f'(x) = 3{x^2} – \frac{{48}}{{{x^2}}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(3{x^2}\) , (A1) for \( – 48\) , (A1) for \({x^{ – 2}}\) . Award a maximum of (A1)(A1)(A0) if extra terms seen.[3 marks]
\(f'(2) = 3{(2)^2} – \frac{{48}}{{{{(2)}^2}}}\) (M1)
Note: Award (M1) for substitution of \(x = 2\) into their derivative.
\(= 0\) (A1)(ft)(G1)[2 marks]
\(( – 2{\text{, }} – 32)\) or \(x = – 2\), \(y = – 32\) (G1)(G1)
Notes: Award (G0)(G0) for \(x = – 32\), \(y = – 2\) . Award at most (G0)(G1) if parentheses are omitted.[2 marks]
\(\{ y \geqslant 32\} \cup \{ y \leqslant – 32\} \) (A1)(A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) \(y \geqslant 32\) or \(y > 32\) seen, (A1)(ft) for \(y \leqslant – 32\) or \(y < – 32\) , (A1) for weak (non-strict) inequalities used in both of the above.
Accept use of \(f\) in place of \(y\). Accept alternative interval notation.
Follow through from their (a) and (e).
If domain is given award (A0)(A0)(A0).
Award (A0)(A1)(ft)(A1)(ft) for \([ – 200{\text{, }} – 32]\) , \([32{\text{, }}200]\).
Award (A0)(A1)(ft)(A1)(ft) for \(] – 200{\text{, }} – 32]\) , \([32{\text{, }}200[\).[3 marks]
\(f'(1) = – 45\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for \(f'(1)\) seen or substitution of \(x = 1\) into their derivative. Follow through from their derivative if working is seen.[2 marks]
\(x = – 1\) (M1)(A1)(ft)(G2)
Notes: Award (M1) for equating their derivative to their \( – 45\) or for seeing parallel lines on their graph in the approximately correct position.[2 marks]
Question
Consider the function \(f(x) = 0.5{x^2} – \frac{8}{x},{\text{ }}x \ne 0\).
Find \(f( – 2)\).[2]
Find \(f'(x)\).[3]
Find the gradient of the graph of \(f\) at \(x = – 2\).[2]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
Write down the equation of \(T\).[2]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
Sketch the graph of \(f\) for \( – 5 \leqslant x \leqslant 5\) and \( – 20 \leqslant y \leqslant 20\).[4]
Let \(T\) be the tangent to the graph of \(f\) at \(x = – 2\).
Draw \(T\) on your sketch.[2]
The tangent, \(T\), intersects the graph of \(f\) at a second point, P.
Use your graphic display calculator to find the coordinates of P.[2]
Answer/Explanation
Markscheme
\(0.5 \times {( – 2)^2} – \frac{8}{{ – 2}}\) (M1)
Note: Award (M1) for substitution of \(x = – 2\) into the formula of the function.
\(6\) (A1)(G2)
\(f'(x) = x + 8{x^{ – 2}}\) (A1)(A1)(A1)
Notes: Award (A1) for \(x\), (A1) for \(8\), (A1) for \({x^{ – 2}}\) or \(\frac{1}{{{x^2}}}\) (each term must have correct sign). Award at most (A1)(A1)(A0) if there are additional terms present or further incorrect simplifications are seen.
\(f'( – 2) = – 2 + 8{( – 2)^{ – 2}}\) (M1)
Note: Award (M1) for \(x = – 2\) substituted into their \(f'(x)\) from part (b).
\( = 0\) (A1)(ft)(G2)
Note: Follow through from their derivative function.
\(y = 6\;\;\;\)OR\(\;\;\;y = 0x + 6\;\;\;\)OR\(\;\;\;y – 6 = 0(x + 2)\) (A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for their gradient from part (c), (A1)(ft) for their answer from part (a). Answer must be an equation.
Award (A0)(A0) for \(x = 6\).
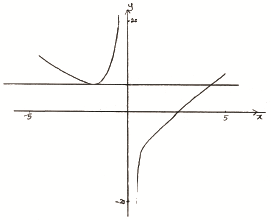(A1)(A1)(A1)(A1)
Notes: Award (A1) for labels and some indication of scales in the stated window. The point \((-2,{\text{ }}6)\) correctly labelled, or an \(x\)-value and a \(y\)-value on their axes in approximately the correct position, are acceptable indication of scales.
Award (A1) for correct general shape (curve must be smooth and must not cross the \(y\)-axis).
Award (A1) for \(x\)-intercept in approximately the correct position.
Award (A1) for local minimum in the second quadrant.
Tangent to graph drawn approximately at \(x = – 2\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for straight line tangent to curve at approximately \(x = – 2\), with approximately correct gradient. Tangent must be straight for the (A1)(ft) to be awarded.
Award (A1)(ft) for (extended) line passing through approximately their \(y\)-intercept from (d). Follow through from their gradient in part (c) and their equation in part (d).
\((4,{\text{ }}6)\;\;\;\)OR\(\;\;\;x = 4,{\text{ }}y = 6\) (G1)(ft)(G1)(ft)
Notes: Follow through from their tangent from part (d). If brackets are missing then award (G0)(G1)(ft).
If line intersects their graph at more than one point (apart from \(( – 2,{\text{ }}6)\)), follow through from the first point of intersection (to the right of \( – 2\)).
Award (G0)(G0) for \(( – 2,{\text{ }}6)\).
Question
Consider the function \(g(x) = {x^3} + k{x^2} – 15x + 5\).
The tangent to the graph of \(y = g(x)\) at \(x = 2\) is parallel to the line \(y = 21x + 7\).
Find \(g'(x)\).[3]
Show that \(k = 6\).[2]
Find the equation of the tangent to the graph of \(y = g(x)\) at \(x = 2\). Give your answer in the form \(y = mx + c\).[3]
Use your answer to part (a) and the value of \(k\), to find the \(x\)-coordinates of the stationary points of the graph of \(y = g(x)\).[3]
Find \(g’( – 1)\).[2]
Hence justify that \(g\) is decreasing at \(x = – 1\).[1]
Find the \(y\)-coordinate of the local minimum.[2]
Answer/Explanation
Markscheme
\(3{x^2} + 2kx – 15\) (A1)(A1)(A1)
Note: Award (A1) for \(3{x^2}\), (A1) for \(2kx\) and (A1) for \( – 15\). Award at most (A1)(A1)(A0) if additional terms are seen.[3 marks]
\(21 = 3{(2)^2} + 2k(2) – 15\) (M1)(M1)
Note: Award (M1) for equating their derivative to 21. Award (M1) for substituting 2 into their derivative. The second (M1) should only be awarded if correct working leads to the final answer of \(k = 6\).
Substituting in the known value, \(k = 6\), invalidates the process; award (M0)(M0).
\(k = 6\) (AG)[2 marks]
\(g(2) = {(2)^3} + (6){(2)^2} – 15(2) + 5{\text{ }}( = 7)\) (M1)
Note: Award (M1) for substituting 2 into \(g\).
\(7 = 21(2) + c\) (M1)
Note: Award (M1) for correct substitution of 21, 2 and their 7 into gradient intercept form.
OR
\(y – 7 = 21(x – 2)\) (M1)
Note: Award (M1) for correct substitution of 21, 2 and their 7 into gradient point form.
\(y = 21x – 35\) (A1) (G2)[3 marks]
\(3{x^2} + 12x – 15 = 0\) (or equivalent) (M1)
Note: Award (M1) for equating their part (a) (with \(k = 6\) substituted) to zero.
\(x = – 5,{\text{ }}x = 1\) (A1)(ft)(A1)(ft)
Note: Follow through from part (a).[3 marks]
\(3{( – 1)^2} + 12( – 1) – 15\) (M1)
Note: Award (M1) for substituting \( – 1\) into their derivative, with \(k = 6\) substituted. Follow through from part (a).
\( = – 24\) (A1)(ft) (G2)[2 marks]
\(g’( – 1) < 0\) (therefore \(g\) is decreasing when \(x = – 1\)) (R1)[1 marks]
\(g(1) = {(1)^3} + (6){(1)^2} – 15(1) + 5\) (M1)
Note: Award (M1) for correctly substituting 6 and their 1 into \(g\).
\( = – 3\) (A1)(ft) (G2)
Note: Award, at most, (M1)(A0) or (G1) if answer is given as a coordinate pair. Follow through from part (c).[2 marks]
Question
Consider the function \(f(x) = – {x^4} + a{x^2} + 5\), where \(a\) is a constant. Part of the graph of \(y = f(x)\) is shown below.
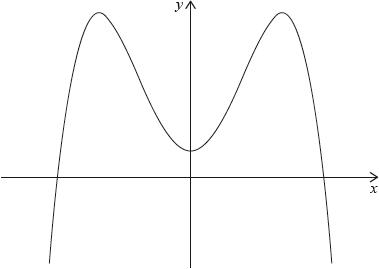
It is known that at the point where \(x = 2\) the tangent to the graph of \(y = f(x)\) is horizontal.
There are two other points on the graph of \(y = f(x)\) at which the tangent is horizontal.
Write down the \(y\)-intercept of the graph.[1]
Find \(f'(x)\).[2]
Show that \(a = 8\).[2]
Find \(f(2)\).[2]
Write down the \(x\)-coordinates of these two points;[2]
Write down the intervals where the gradient of the graph of \(y = f(x)\) is positive.[2]
Write down the range of \(f(x)\).[2]
Write down the number of possible solutions to the equation \(f(x) = 5\).[1]
The equation \(f(x) = m\), where \(m \in \mathbb{R}\), has four solutions. Find the possible values of \(m\).[2]
Answer/Explanation
Markscheme
5 (A1)
Note: Accept an answer of \((0,{\text{ }}5)\).[1 mark]
\(\left( {f'(x) = } \right) – 4{x^3} + 2ax\) (A1)(A1)
Note: Award (A1) for \( – 4{x^3}\) and (A1) for \( + 2ax\). Award at most (A1)(A0) if extra terms are seen.[2 marks]
\( – 4 \times {2^3} + 2a \times 2 = 0\) (M1)(M1)
Note: Award (M1) for substitution of \(x = 2\) into their derivative, (M1) for equating their derivative, written in terms of \(a\), to 0 leading to a correct answer (note, the 8 does not need to be seen).
\(a = 8\) (AG)[2 marks]
\(\left( {f(2) = } \right) – {2^4} + 8 \times {2^2} + 5\) (M1)
Note: Award (M1) for correct substitution of \(x = 2\) and \(a = 8\) into the formula of the function.
21 (A1)(G2)[2 marks]
\((x = ){\text{ }} – 2,{\text{ }}(x = ){\text{ 0}}\) (A1)(A1)
Note: Award (A1) for each correct solution. Award at most (A0)(A1)(ft) if answers are given as \(( – 2{\text{ }},21)\) and \((0,{\text{ }}5)\) or \(( – 2,{\text{ }}0)\) and \((0,{\text{ }}0)\).[2 marks]
\(x < – 2,{\text{ }}0 < x < 2\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for \(x < – 2\), follow through from part (d)(i) provided their value is negative.
Award (A1)(ft) for \(0 < x < 2\), follow through only from their 0 from part (d)(i); 2 must be the upper limit.
Accept interval notation.[2 marks]
\(y \leqslant 21\) (A1)(ft)(A1)
Notes: Award (A1)(ft) for 21 seen in an interval or an inequality, (A1) for “\(y \leqslant \)”.
Accept interval notation.
Accept \( – \infty < y \leqslant 21\) or \(f(x) \leqslant 21\).
Follow through from their answer to part (c)(ii). Award at most (A1)(ft)(A0) if \(x\) is seen instead of \(y\). Do not award the second (A1) if a (finite) lower limit is seen.[2 marks]
3 (solutions) (A1)[1 mark]
\(5 < m < 21\) or equivalent (A1)(ft)(A1)
Note: Award (A1)(ft) for 5 and 21 seen in an interval or an inequality, (A1) for correct strict inequalities. Follow through from their answers to parts (a) and (c)(ii).
Accept interval notation.[2 marks]
Question
Consider the curve y = 2x3 − 9x2 + 12x + 2, for −1 < x < 3
Sketch the curve for −1 < x < 3 and −2 < y < 12.[4]
A teacher asks her students to make some observations about the curve.
Three students responded.
Nadia said “The x-intercept of the curve is between −1 and zero”.
Rick said “The curve is decreasing when x < 1 ”.
Paula said “The gradient of the curve is less than zero between x = 1 and x = 2 ”.
State the name of the student who made an incorrect observation.[1]
Find the value of y when x = 1 .[2]
Find \(\frac{{{\text{dy}}}}{{{\text{dx}}}}\).[3]
Show that the stationary points of the curve are at x = 1 and x = 2.[2]
Given that y = 2x3 − 9x2 + 12x + 2 = k has three solutions, find the possible values of k.[3]
Answer/Explanation
Markscheme
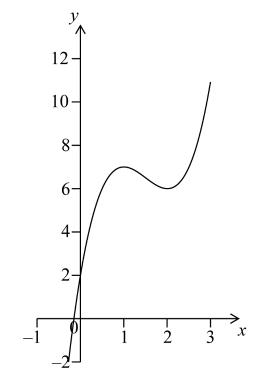(A1)(A1)(A1)(A1)
Note: Award (A1) for correct window (condone a window which is slightly off) and axes labels. An indication of window is necessary. −1 to 3 on the x-axis and −2 to 12 on the y-axis and a graph in that window.
(A1) for correct shape (curve having cubic shape and must be smooth).
(A1) for both stationary points in the 1st quadrant with approximate correct position,
(A1) for intercepts (negative x-intercept and positive y intercept) with approximate correct position.[4 marks]
Rick (A1)
Note: Award (A0) if extra names stated.[1 mark]
2(1)3 − 9(1)2 + 12(1) + 2 (M1)
Note: Award (M1) for correct substitution into equation.
= 7 (A1)(G2)[2 marks]
6x2 − 18x + 12 (A1)(A1)(A1)
Note: Award (A1) for each correct term. Award at most (A1)(A1)(A0) if extra terms seen.[3 marks]
6x2 − 18x + 12 = 0 (M1)
Note: Award (M1) for equating their derivative to 0. If the derivative is not explicitly equated to 0, but a subsequent solving of their correct equation is seen, award (M1).
6(x − 1)(x − 2) = 0 (or equivalent) (M1)
Note: Award (M1) for correct factorization. The final (M1) is awarded only if answers are clearly stated.
Award (M0)(M0) for substitution of 1 and of 2 in their derivative.
x = 1, x = 2 (AG)[2 marks]
6 < k < 7 (A1)(A1)(ft)(A1)
Note: Award (A1) for an inequality with 6, award (A1)(ft) for an inequality with 7 from their part (c) provided it is greater than 6, (A1) for their correct strict inequalities. Accept ]6, 7[ or (6, 7).[3 marks]