Question
G is a simple, connected, planar graph with 9 vertices and e edges.
(a) Find the maximum possible value of e . [2]
The complement of G has e , edges.
(b) Find an expression for e , in terms of e . [2]
(c) Given that the complement of G is also planar and connected, find the possible values of e . [2]
H is a simple graph with v vertices and e edges.
(d) Given that both H and its complement are planar and connected, find the maximum possible value of v . [5]
▶️Answer/Explanation
Ans:
(a)
substitutes v=9 into either e = 3v-6 or \(e\leq 3v-6\) the maximum number of edges is 21 (e ≤ 21)
(b)
\(k_{9}\) has\( (_{2}^{9}=)\)36 edges
so \(e = 36-e (=(_{2}^{9})-e)\)
(c)
e’\( \leq 21\Rightarrow 36 – e \leq 21\)
\(15 \leq e \leq21\) (the possible values are 15,16,17,18,19,20,and 21)
(d)
recognises that \(e+e = \frac{v(v-1)}{2}\)(or equivalent)
uses \( e\leq 3v-6 \)and \(e\leq 3v-6\)
to form \(\frac{v(v-1)}{2}-(3v-6)\leq 3v-6\)
attempts to solve their quadratic inequality (equality)
\(v^{2}-13v+24\leq 0\Rightarrow 2.228…\leq v\leqslant 10.77…\)
the maximum possible value of v is \(10 (v\leq 10)\)
Question
a.The weighted graph H is shown below.
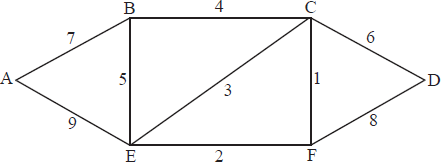
Use Kruskal’s Algorithm, indicating the order in which the edges are added, to find and draw the minimum spanning tree for H.[6]
(ii) We will call a graph with v vertices a “forest” if it consists of c components each of which is a tree.
Here is an example of a forest with 4 components.
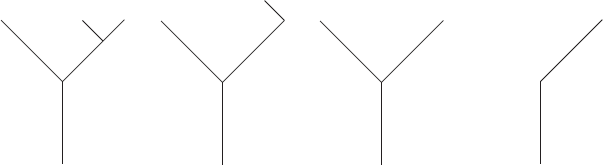
How many edges will a forest with v vertices and c components have?[5]
▶️Answer/Explanation
Markscheme
The edges are included in the order
CF A1
EF A1
BC A1
CD A1
AB A1
 A1
A1
[6 marks]
(i) A tree with v vertices has v −1 edges. A1
Using v + f = e + 2 with f = 1, the result follows. R1
(ii) Each of the c trees will have one less edge than the number of vertices. R1
Thus the forest will have v − c edges. A2
[5 marks]
Examiners report
In (a), many candidates derived the minimum spanning tree although in some cases the method was not clearly indicated as required and some candidates used an incorrect algorithm. Part (b) was reasonably answered by many candidates although some justifications were unsatisfactory. Part (c) caused problems for many candidates who found difficulty in writing down a rigorous proof of the required result.
In (a), many candidates derived the minimum spanning tree although in some cases the method was not clearly indicated as required and some candidates used an incorrect algorithm. Part (b) was reasonably answered by many candidates although some justifications were unsatisfactory. Part (c) caused problems for many candidates who found difficulty in writing down a rigorous proof of the required result.
Question
a.A graph has n vertices with degrees 1, 2, 3, …, n. Prove that \(n \equiv 0(\bmod 4)\) or \(n \equiv 3(\bmod 4)\).[6]
b.Let G be a simple graph with n vertices, \(n \geqslant 2\). Prove, by contradiction, that at least two of the vertices of G must have the same degree.[8]
▶️Answer/Explanation
Markscheme
as each edge contributes 1 to each of the vertices that it is incident with, each edge will contribute 2 to the sum of the degrees of all the vertices (R1)
so \(2e = \sum {{\text{degrees}}} \) (A1)
\(2e = \frac{{n(n + 1)}}{2}\) A1
\(4|n(n + 1)\) A1
n and n + 1 are coprime R1
Note: Accept equivalent reasoning e.g. only one of n and n + 1 can be even.
\(4|n{\text{ or }}4|n + 1\) A1
\(n \equiv 0(\bmod 4){\text{ or }}n \equiv 3(\bmod 4)\) AG
[6 marks]
since G is simple, the highest degree that a vertex can have is n – 1 R1
the degrees of the vertices must belong to the set \(S = \{ 0,{\text{ }}1,{\text{ }}2,{\text{ }} \ldots ,{\text{ }}n – 1\} \) A1
proof by contradiction
if no two vertices have the same degree, all n vertices must have different degrees R1
as there are only n different degrees in set S, the degrees must be precisely the n numbers 0, 1, 2, …, n – 1 R1
let the vertex with degree 0 be A, then A is not adjacent to any of the other vertices R1
let the vertex with degree n – 1 be B, then B is adjacent to all of the other vertices including A R1R1
this is our desired contradiction, so there must be two vertices of the same degree R1
[8 marks]
Examiners report
Only the top candidates were able to produce logically, well thought-out proofs.
Only the top candidates were able to produce logically, well thought-out proofs.
Question
a.In any graph, show that
(i) the sum of the degrees of all the vertices is even;
(ii) there is an even number of vertices of odd degree.[5]
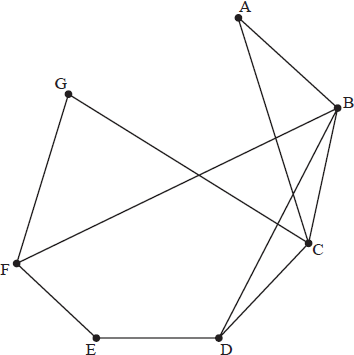
(i) Show that M is planar.
(ii) Explain why M is not Eulerian.
(iii) By adding one edge to M it is possible to make it Eulerian. State which edge must be added.
This new graph is called N.
(iv) Starting at A, write down a possible Eulerian circuit for N.
(v) Define a Hamiltonian cycle. If possible, write down a Hamiltonian cycle for N, and if not possible, give a reason.
(vi) Write down the adjacency matrix for N.
(vii) Which pair of distinct vertices has exactly 30 walks of length 4 between them?[12]
▶️Answer/Explanation
Markscheme
(i) When we sum over the degrees of all vertices, we count each edge twice. Hence every edge adds two to the sum. Hence the sum of the degrees of all the vertices is even. R2
(ii) divide the vertices into two sets, those with even degree and those with odd degree M1
let S be the sum of the degrees of the first set and let T be the sum of the degrees of the second set
we know S + T must be even
since S is the sum of even numbers, then it is even R1
hence T must be even R1
hence there must be an even number of vertices of odd degree AG
[5 marks]
(i)
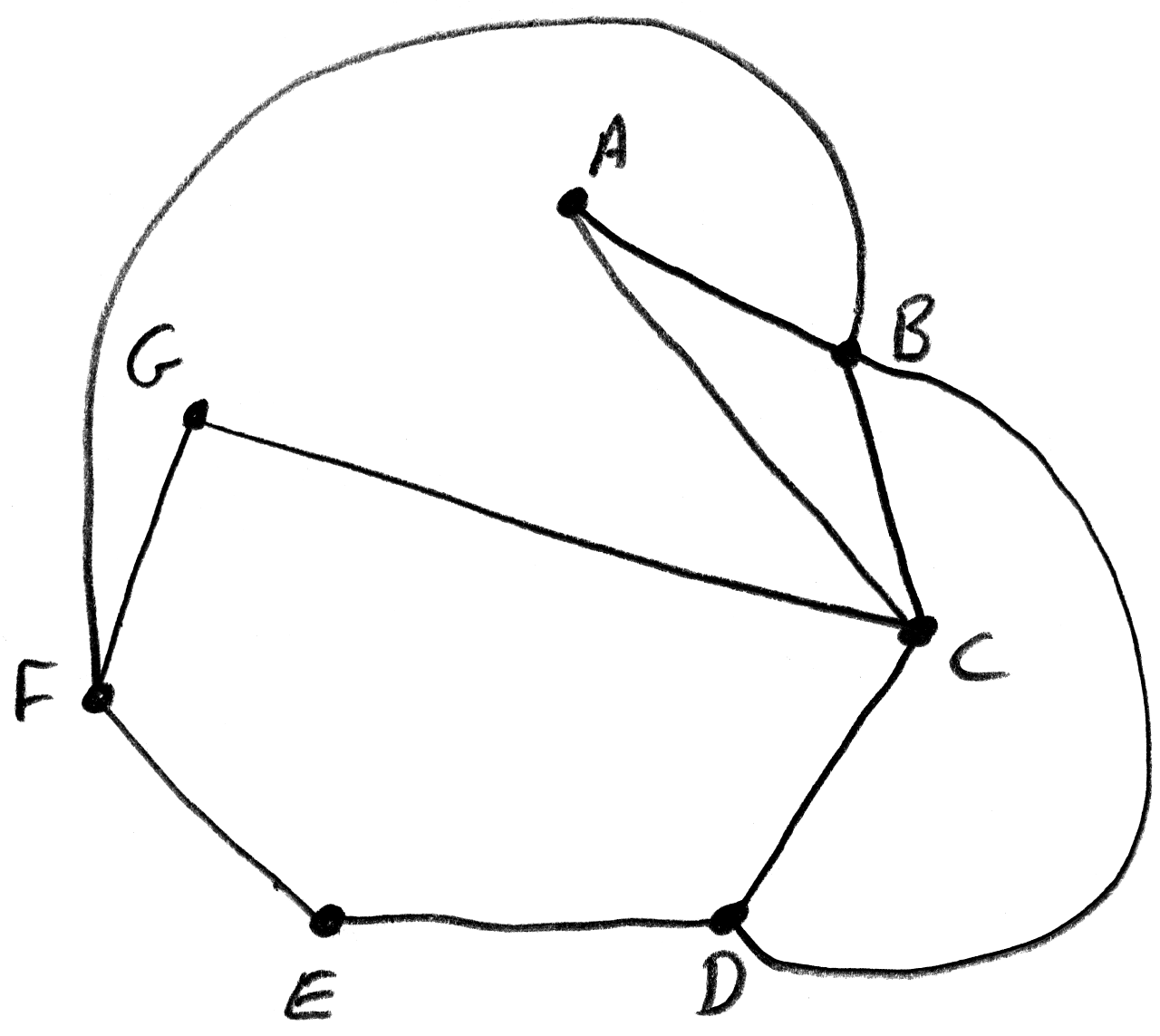 A1
A1
(ii) the graph M is not Eulerian because vertices D and F are of odd degree A1
(iii) the edge which must be added is DF A1
(iv)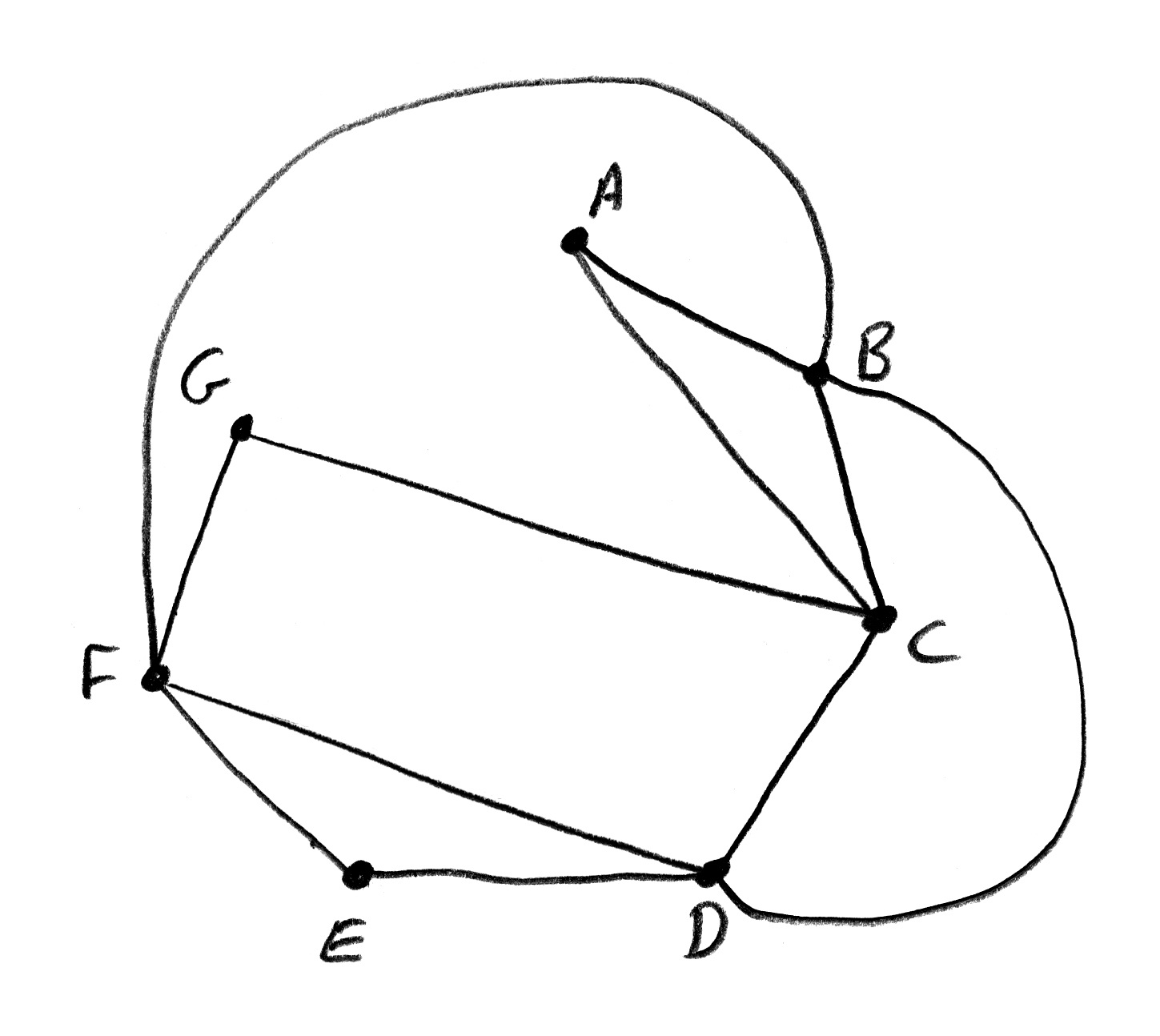
a possible Eulerian circuit is ABDFBCDEFGCA A2
Note: award A1 for a correct Eulerian circuit not starting and finishing at A.
(v) a Hamiltonian cycle is one that contains each vertex in N A1
with the exception of the starting and ending vertices, each vertex must only appear once A1
a possible Hamiltonian cycle is ACGFEDBA A1
(vi) \(\left( {\begin{array}{*{20}{c}}
0&1&1&0&0&0&0 \\
1&0&1&1&0&1&0 \\
1&1&0&1&0&0&1 \\
0&1&1&0&1&1&0 \\
0&0&0&1&0&1&0 \\
0&1&0&1&1&0&1 \\
0&0&1&0&0&1&0
\end{array}} \right)\) A2
(vii) using adjacency matrix to power 4 (M1)
C and F A1
[12 marks]
Examiners report
Most candidates were able to start (a), but many found problems in expressing their ideas clearly in words. Stronger candidates had little problem with (b), but a significant number of weaker candidates had problems working with the concepts of Eulerian circuits and Hamiltonian cycles and with understanding how to find a specific number of walks of a certain length as required in (b) (vii).
Most candidates were able to start (a), but many found problems in expressing their ideas clearly in words. Stronger candidates had little problem with (b), but a significant number of weaker candidates had problems working with the concepts of Eulerian circuits and Hamiltonian cycles and with understanding how to find a specific number of walks of a certain length as required in (b) (vii).
Question
The graph G has adjacency matrix M given below.

a.Draw the graph G .[2]
b.What information about G is contained in the diagonal elements of M\(^2\) ?[1]
d.List the trails of length 4 starting at A and ending at C.[3]
▶️Answer/Explanation
Markscheme
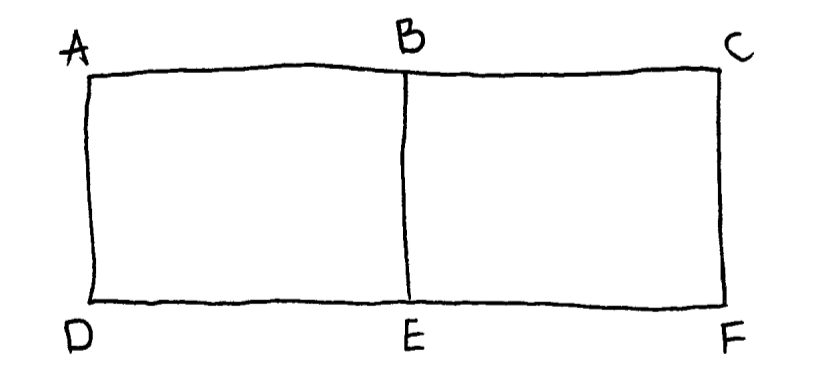 A2
A2
Note: Award A1 if only one error, A0 for two or more.
[2 marks]
the (k, k) element of M\(^2\) is the number of vertices directly connected to vertex k A1
Note: Accept comment about the number of walks of length 2, in which the initial and final vertices coincide.
[1 mark]
the trails of length 4 are ABEDC, AFEDC, AFEBC A1A1A1
Note: A1A1A1 for three correct with no additions; A1A1A0 for all correct, but with additions; A1A0A0 for two correct with or without additions.
[3 marks]
Examiners report
Parts (a) and (c) were generally correctly answered. In part (b), a minority of candidates failed to mention that the starting and end points had to coincide. A large number of candidates gave all walks (trails were asked for) – an unnecessary loss of marks.
Parts (a) and (c) were generally correctly answered. In part (b), a minority of candidates failed to mention that the starting and end points had to coincide. A large number of candidates gave all walks (trails were asked for) – an unnecessary loss of marks.
Parts (a) and (c) were generally correctly answered. In part (b), a minority of candidates failed to mention that the starting and end points had to coincide. A large number of candidates gave all walks (trails were asked for) – an unnecessary loss of marks.
