Download IITian Academy App for accessing Online Mock Tests and More..
Question
Let \(f(x) = \ln (x + 5) + \ln 2\) , for \(x > – 5\) .
Find \({f^{ – 1}}(x)\) .
Let \(g(x) = {{\rm{e}}^x}\) .
Find \((g \circ f)(x)\) , giving your answer in the form \(ax + b\) , where \(a,b \in \mathbb{Z}\) .
Answer/Explanation
Markscheme
METHOD 1
\(\ln (x + 5) + \ln 2 = \ln (2(x + 5))\) \(( = \ln (2x + 10))\) (A1)
interchanging x and y (seen anywhere) (M1)
e.g. \(x = \ln (2y + 10)\)
evidence of correct manipulation (A1)
e.g. \({{\rm{e}}^x} = 2y + 10\)
\({f^{ – 1}}(x) = \frac{{{{\rm{e}}^x} – 10}}{2}\) A1 N2
METHOD 2
\(y = \ln (x + 5) + \ln 2\)
\(y – \ln 2 = ln(x + 5)\) (A1)
evidence of correct manipulation (A1)
e.g. \({{\rm{e}}^{y – \ln 2}} = x + 5\)
interchanging x and y (seen anywhere) (M1)
e.g. \({{\rm{e}}^{x – \ln 2}} = y + 5\)
\({f^{ – 1}}(x) = {{\rm{e}}^{x – \ln 2}} – 5\) A1 N2
[4 marks]
METHOD 1
evidence of composition in correct order (M1)
e.g. \((g \circ f)(x) = g(\ln (x + 5) + \ln 2)\)
\( = {{\rm{e}}^{\ln (2(x + 5))}} = 2(x + 5)\)
\((g \circ f)(x) = 2x + 10\) A1A1 N2
METHOD 2
evidence of composition in correct order (M1)
e.g. \((g \circ f)(x) = {{\rm{e}}^{\ln (x + 5) + \ln 2}}\)
\( = {{\rm{e}}^{\ln (x + 5)}} \times {{\rm{e}}^{\ln 2}} = (x + 5)2\)
\((g \circ f)(x) = 2x + 10\) A1A1 N2
[3 marks]
Question
Let \(f(x) = {x^2}\) and \(g(x) = 2x – 3\) .
Find \({g^{ – 1}}(x)\) .
Find \((f \circ g)(4)\) .
Answer/Explanation
Markscheme
for interchanging x and y (may be done later) (M1)
e.g. \(x = 2y – 3\)
\({g^{ – 1}}(x) = \frac{{x + 3}}{2}\) (accept \(y = \frac{{x + 3}}{2},\frac{{x + 3}}{2}\) ) A1 N2
[2 marks]
METHOD 1
\(g(4) = 5\) (A1)
evidence of composition of functions (M1)
\(f(5) = 25\) A1 N3
METHOD 2
\(f \circ g(x) = {(2x – 3)^2}\) (M1)
\(f \circ g(4) = {(2 \times 4 – 3)^2}\) (A1)
= 25 A1 N3
[3 marks]
Question
Let \(f(x) = 2{x^3} + 3\) and \(g(x) = {{\rm{e}}^{3x}} – 2\) .
(i) Find \(g(0)\) .
(ii) Find \((f \circ g)(0)\) .
Find \({f^{ – 1}}(x)\) .
Answer/Explanation
Markscheme
(i) \(g(0) = {{\rm{e}}^0} – 2\) (A1)
\( = – 1\) A1 N2
(ii) METHOD 1
substituting answer from (i) (M1)
e.g. \((f \circ g)(0) = f( – 1)\)
correct substitution \(f( – 1) = 2{( – 1)^3} + 3\) (A1)
\(f( – 1) = 1\) A1 N3
METHOD 2
attempt to find \((f \circ g)(x)\) (M1)
e.g. \((f \circ g)(x) = f({{\rm{e}}^{3x}} – 2)\) \( = 2{({{\rm{e}}^{3x}} – 2)^3} + 3\)
correct expression for \((f \circ g)(x)\) (A1)
e.g. \(2{({{\rm{e}}^{3x}} – 2)^3} + 3\)
\((f \circ g)(0) = 1\) A1 N3
[5 marks]
interchanging x and y (seen anywhere) (M1)
e.g. \(x = 2{y^3} + 3\)
attempt to solve (M1)
e.g. \({y^3} = \frac{{x – 3}}{2}\)
\({f^{ – 1}}(x) = \sqrt[3]{{\frac{{x – 3}}{2}}}\) A1 N3
[3 marks]
Question
Let \(f(x) = lo{g_3}\sqrt x \) , for \(x > 0\) .
Show that \({f^{ – 1}}(x) = {3^{2x}}\) .
Write down the range of \({f^{ – 1}}\) .
Let \(g(x) = {\log _3}x\) , for \(x > 0\) .
Find the value of \(({f^{ – 1}} \circ g)(2)\) , giving your answer as an integer.
Answer/Explanation
Markscheme
interchanging x and y (seen anywhere) (M1)
e.g. \(x = \log \sqrt y \) (accept any base)
evidence of correct manipulation A1
e.g. \(3^x = \sqrt y \) , \({3^y} = {x^{\frac{1}{2}}}\) , \(x = \frac{1}{2}{\log _3}y\) , \(2y = {\log _3}x\)
\({f^{ – 1}}(x) = {3^{2x}}\) AG N0
[2 marks]
\(y > 0\) , \({f^{ – 1}}(x) > 0\) A1 N1
[1 mark]
METHOD 1
finding \(g(2) = lo{g_3}2\) (seen anywhere) A1
attempt to substitute (M1)
e.g. \(({f^{ – 1}} \circ g)(2) = {3^{2\log {_3}2}}\)
evidence of using log or index rule (A1)
e.g. \(({f^{ – 1}} \circ g)(2) = {3^{\log {_3}4}}\) , \({3^{{{\log }_3}2^2}}\)
\(({f^{ – 1}} \circ g)(2) = 4\) A1 N1
METHOD 2
attempt to form composite (in any order) (M1)
e.g. \(({f^{ – 1}} \circ g)(x) = {3^{2{{\log }_3}x}}\)
evidence of using log or index rule (A1)
e.g. \(({f^{ – 1}} \circ g)(x) = {3^{{{\log }_3}{x^2}}}\) , \({3^{{{\log }_3}{x^{}}}}^2\)
\(({f^{ – 1}} \circ g)(x) = {x^2}\) A1
\(({f^{ – 1}} \circ g)(2) = 4\) A1 N1
[4 marks]
Question
Let \(f(x) = \cos 2x\) and \(g(x) = 2{x^2} – 1\) .
Find \(f\left( {\frac{\pi }{2}} \right)\) .
Find \((g \circ f)\left( {\frac{\pi }{2}} \right)\) .
Given that \((g \circ f)(x)\) can be written as \(\cos (kx)\) , find the value of k, \(k \in \mathbb{Z}\) .
Answer/Explanation
Markscheme
\(f\left( {\frac{\pi }{2}} \right) = \cos \pi \) (A1)
\( = – 1\) A1 N2
[2 marks]
\((g \circ f)\left( {\frac{\pi }{2}} \right) = g( – 1)\) \(( = 2{( – 1)^2} – 1)\) (A1)
\(= 1\) A1 N2
[2 marks]
\((g \circ f)(x) = 2{(\cos (2x))^2} – 1\) \(( = 2{\cos ^2}(2x) – 1)\) A1
evidence of \(2{\cos ^2}\theta – 1 = \cos 2\theta \) (seen anywhere) (M1)
\((g \circ f)(x) = \cos 4x\)
\(k = 4\) A1 N2
[3 marks]
Question
Let \(f(x) = {x^2} + 4\) and \(g(x) = x – 1\) .
Find \((f \circ g)(x)\) .
The vector \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 1}
\end{array}} \right)\) translates the graph of \((f \circ g)\) to the graph of h .
Find the coordinates of the vertex of the graph of h .
The vector \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 1}
\end{array}} \right)\) translates the graph of \((f \circ g)\) to the graph of h .
Show that \(h(x) = {x^2} – 8x + 19\) .
The vector \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 1}
\end{array}} \right)\) translates the graph of \((f \circ g)\) to the graph of h .
The line \(y = 2x – 6\) is a tangent to the graph of h at the point P. Find the x-coordinate of P.
Answer/Explanation
Markscheme
attempt to form composition (in any order) (M1)
\((f \circ g)(x) = {(x – 1)^2} + 4\) \(({x^2} – 2x + 5)\) A1 N2
[2 marks]
METHOD 1
vertex of \(f \circ g\) at (1, 4) (A1)
evidence of appropriate approach (M1)
e.g. adding \(\left( {\begin{array}{*{20}{c}}
3\\
{ – 1}
\end{array}} \right)\) to the coordinates of the vertex of \(f \circ g\)
vertex of h at (4, 3) A1 N3
METHOD 2
attempt to find \(h(x)\) (M1)
e.g. \({((x – 3) – 1)^2} + 4 – 1\) , \(h(x) = (f \circ g)(x – 3) – 1\)
\(h(x) = {(x – 4)^2} + 3\) (A1)
vertex of h at (4, 3) A1 N3
[3 marks]
evidence of appropriate approach (M1)
e.g. \({(x – 4)^2} + 3\) ,\({(x – 3)^2} – 2(x – 3) + 5 – 1\)
simplifying A1
e.g. \(h(x) = {x^2} – 8x + 16 + 3\) , \({x^2} – 6x + 9 – 2x + 6 + 4\)
\(h(x) = {x^2} – 8x + 19\) AG N0
[2 marks]
METHOD 1
equating functions to find intersection point (M1)
e.g. \({x^2} – 8x + 19 = 2x – 6\) , \(y = h(x)\)
\({x^2} – 10x + 25 + 0\) A1
evidence of appropriate approach to solve (M1)
e.g. factorizing, quadratic formula
appropriate working A1
e.g. \({(x – 5)^2} = 0\)
\(x = 5\) \((p = 5)\) A1 N3
METHOD 2
attempt to find \(h'(x)\) (M1)
\(h(x) = 2x – 8\) A1
recognizing that the gradient of the tangent is the derivative (M1)
e.g. gradient at \(p = 2\)
\(2x – 8 = 2\) \((2x = 10)\) A1
\(x = 5\) A1 N3
[5 marks]
Question
Let \(f(x) = 7 – 2x\) and \(g(x) = x + 3\) .
Find \((g \circ f)(x)\) .
Write down \({g^{ – 1}}(x)\) .
Find \((f \circ {g^{ – 1}})(5)\) .
Answer/Explanation
Markscheme
attempt to form composite (M1)
e.g. \(g(7 – 2x)\) , \(7 – 2x + 3\)
\((g \circ f)(x) = 10 – 2x\) A1 N2
[2 marks]
\({g^{ – 1}}(x) = x – 3\) A1 N1
[1 mark]
METHOD 1
valid approach (M1)
e.g. \({g^{ – 1}}(5)\) , \(2\) , \(f(5)\)
\(f(2) = 3\) A1 N2
METHOD 2
attempt to form composite of f and \({g^{ – 1}}\) (M1)
e.g. \((f \circ {g^{ – 1}})(x) = 7 – 2(x – 3)\) , \(13 – 2x\)
\((f \circ {g^{ – 1}})(5) = 3\) A1 N2
[2 marks]
Question
Let \(f(x) = 2x – 1\) and \(g(x) = 3{x^2} + 2\) .
Find \({f^{ – 1}}(x)\) .
Find \((f \circ g)(1)\) .
Answer/Explanation
Markscheme
interchanging x and y (seen anywhere) (M1)
e.g. \(x = 2y – 1\)
correct manipulation (A1)
e.g. \(x + 1 = 2y\)
\({f^{ – 1}}(x) = \frac{{x + 1}}{2}\) A1 N2
[3 marks]
METHOD 1
attempt to find or \(g(1)\) or \(f(1)\) (M1)
\(g(1) = 5\) (A1)
\(f(5) = 9\) A1 N2
[3 marks]
METHOD 2
attempt to form composite (in any order) (M1)
e.g. \(2(3{x^2} + 2) – 1\) , \(3{(2x – 1)^2} + 2\)
\((f \circ g)(1) = 2(3 \times {1^2} + 2) – 1\) \(( = 6 \times {1^2} + 3)\) (A1)
\((f \circ g)(1) = 9\) A1 N2
[3 marks]
Question
Let \(f(x) = \sqrt {x – 5} \) , for \(x \ge 5\) .
Find \({f^{ – 1}}(2)\) .
Let \(g\) be a function such that \({g^{ – 1}}\) exists for all real numbers. Given that \(g(30) = 3\) , find \((f \circ {g^{ – 1}})(3)\) .
Answer/Explanation
Markscheme
METHOD 1
attempt to set up equation (M1)
eg \(2 = \sqrt {y – 5} \) , \(2 = \sqrt {x – 5} \)
correct working (A1)
eg \(4 = y – 5\) , \(x = {2^2} + 5\)
\({f^{ – 1}}(2) = 9\) A1 N2
METHOD 2
interchanging \(x\) and \(y\) (seen anywhere) (M1)
eg \(x = \sqrt {y – 5} \)
correct working (A1)
eg \({x^2} = y – 5\) , \(y = {x^2} + 5\)
\({f^{ – 1}}(2) = 9\) A1 N2
[3 marks]
recognizing \({g^{ – 1}}(3) = 30\) (M1)
eg \(f(30)\)
correct working (A1)
eg \((f \circ {g^{ – 1}})(3) = \sqrt {30 – 5} \) , \(\sqrt {25} \)
\((f \circ {g^{ – 1}})(3) = 5\) A1 N2
Note: Award A0 for multiple values, eg \( \pm 5\) .
[3 marks]
Question
Let \(f(x) = 4x – 2\) and \(g(x) = – 2{x^2} + 8\) .
Find \({f^{ – 1}}(x)\) .
Find \((f \circ g)(1)\) .
Answer/Explanation
Markscheme
interchanging \(x\) and \(y\) (seen anywhere) (M1)
eg \(x = 4y – 2\)
evidence of correct manipulation (A1)
eg \(x + 2 = 4y\)
\({f^{ – 1}}(x) = \frac{{x + 2}}{4}\) (accept \(y = \frac{{x + 2}}{4}\) , \(\frac{{x + 2}}{4}\) , \({f^{ – 1}}(x) = \frac{1}{4}x + \frac{1}{2}\) A1 N2
[3 marks]
METHOD 1
attempt to substitute \(1\) into \(g(x)\) (M1)
eg \(g(1) = – 2 \times {1^2} + 8\)
\(g(1) = 6\) (A1)
\(f(6) = 22\) A1 N3
METHOD 2
attempt to form composite function (in any order) (M1)
eg \((f \circ g)(x) = 4( – 2{x^2} + 8) – 2\) \(( = – 8{x^2} + 30)\)
correct substitution
eg \((f \circ g)(1) = 4( – 2 \times {1^2} + 8) – 2\) , \( – 8 + 30\)
\(f(6) = 22\) A1 N3
[3 marks]
Question
Let \(f(x) = 3x – 2\) and \(g(x) = \frac{5}{{3x}}\), for \(x \ne 0\).
Let \(h(x) = \frac{5}{{x + 2}}\), for \(x \geqslant 0\). The graph of h has a horizontal asymptote at \(y = 0\).
Find \({f^{ – 1}}(x)\).
Show that \(\left( {g \circ {f^{ – 1}}} \right)(x) = \frac{5}{{x + 2}}\).
Find the \(y\)-intercept of the graph of \(h\).
Hence, sketch the graph of \(h\).
For the graph of \({h^{ – 1}}\), write down the \(x\)-intercept;
For the graph of \({h^{ – 1}}\), write down the equation of the vertical asymptote.
Given that \({h^{ – 1}}(a) = 3\), find the value of \(a\).
Answer/Explanation
Markscheme
interchanging \(x\) and \(y\) (M1)
eg \(x = 3y – 2\)
\({f^{ – 1}}(x) = \frac{{x + 2}}{3}{\text{ }}\left( {{\text{accept }}y = \frac{{x + 2}}{3},{\text{ }}\frac{{x + 2}}{3}} \right)\) A1 N2
[2 marks]
attempt to form composite (in any order) (M1)
eg \(g\left( {\frac{{x + 2}}{3}} \right),{\text{ }}\frac{{\frac{5}{{3x}} + 2}}{3}\)
correct substitution A1
eg \(\frac{5}{{3\left( {\frac{{x + 2}}{3}} \right)}}\)
\(\left( {g \circ {f^{ – 1}}} \right)(x) = \frac{5}{{x + 2}}\) AG N0
[2 marks]
valid approach (M1)
eg \(h(0),{\text{ }}\frac{5}{{0 + 2}}\)
\(y = \frac{5}{2}{\text{ }}\left( {{\text{accept (0, 2.5)}}} \right)\) A1 N2
[2 marks]
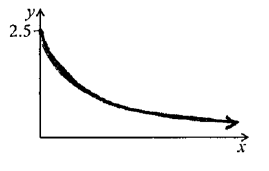
A1A2 N3
Notes: Award A1 for approximately correct shape (reciprocal, decreasing, concave up).
Only if this A1 is awarded, award A2 for all the following approximately correct features: y-intercept at \((0, 2.5)\), asymptotic to x-axis, correct domain \(x \geqslant 0\).
If only two of these features are correct, award A1.
[3 marks]
\(x = \frac{5}{2}{\text{ }}\left( {{\text{accept (2.5, 0)}}} \right)\) A1 N1
[1 mark]
\(x = 0\) (must be an equation) A1 N1
[1 mark]
METHOD 1
attempt to substitute \(3\) into \(h\) (seen anywhere) (M1)
eg \(h(3),{\text{ }}\frac{5}{{3 + 2}}\)
correct equation (A1)
eg \(a = \frac{5}{{3 + 2}},{\text{ }}h(3) = a\)
\(a = 1\) A1 N2
[3 marks]
METHOD 2
attempt to find inverse (may be seen in (d)) (M1)
eg \(x = \frac{5}{{y + 2}},{\text{ }}{h^{ – 1}} = \frac{5}{x} – 2,{\text{ }}\frac{5}{x} + 2\)
correct equation, \(\frac{5}{x} – 2 = 3\) (A1)
\(a = 1\) A1 N2
[3 marks]
Question
The following diagram shows the graph of a function \(f\).
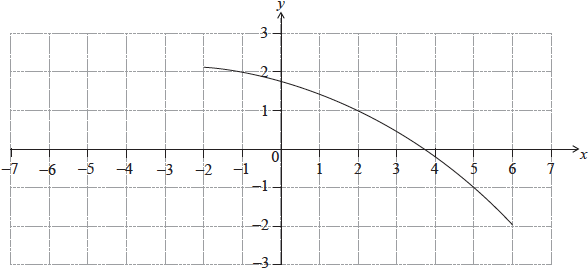
Find \({f^{ – 1}}( – 1)\).
Find \((f \circ f)( – 1)\).
On the same diagram, sketch the graph of \(y = f( – x)\).
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\;\;\;\)horizontal line on graph at \( – 1,{\text{ }}f(a) = – 1,{\text{ }}( – 1,5)\)
\({f^{ – 1}}( – 1) = 5\) A1 N2
[2 marks]
attempt to find \(f( – 1)\) (M1)
eg\(\;\;\;\)line on graph
\(f( – 1) = 2\) (A1)
\((f \circ f)( – 1) = 1\) A1 N3
[3 marks]
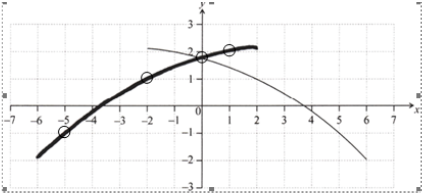A1A1 N2
Note: The shape must be an approximately correct shape (concave down and increasing). Only if the shape is approximately correct, award the following for points in circles:
A1 for the \(y\)-intercept,
A1 for any two of these points \(( – 5,{\text{ }} – 1),{\text{ }}( – 2,{\text{ }}1),{\text{ }}(1,{\text{ }}2)\).
[2 marks]
Total [7 marks]
Question
Let \(f(x) = {(x – 5)^3}\), for \(x \in \mathbb{R}\).
Find \({f^{ – 1}}(x)\).
Let \(g\) be a function so that \((f \circ g)(x) = 8{x^6}\). Find \(g(x)\).
Answer/Explanation
Markscheme
interchanging \(x\) and \(y\) (seen anywhere) (M1)
eg\(\;\;\;x = {(y – 5)^3}\)
evidence of correct manipulation (A1)
eg\(\;\;\;y – 5 = \sqrt[3]{x}\)
\({f^{ – 1}}(x) = \sqrt[3]{x} + 5\;\;\;({\text{accept }}5 + {x^{\frac{1}{3}}},{\text{ }}y = 5 + \sqrt[3]{x})\) A1 N2
Notes: If working shown, and they do not interchange \(x\) and \(y\), award A1A1M0 for \(\sqrt[3]{y} + 5\).
If no working shown, award N1 for \(\sqrt[3]{y} + 5\).
METHOD 1
attempt to form composite (in any order) (M1)
eg\(\;\;\;g\left( {{{(x – 5)}^3}} \right),{\text{ }}{\left( {g(x) – 5} \right)^3} = 8{x^6},{\text{ }}f(2{x^2} + 5)\)
correct working (A1)
eg\(\;\;\;g – 5 = 2{x^2},{\text{ }}{\left( {(2{x^2} + 5) – 5} \right)^3}\)
\(g(x) = 2{x^2} + 5\) A1 N2
METHOD 2
recognising inverse relationship (M1)
eg\(\;\;\;{f^{ – 1}}(8{x^6}) = g(x),{\text{ }}{f^{ – 1}}(f \circ g)(x) = {f^{ – 1}}(8{x^6})\)
correct working
eg\(\;\;\;g(x) = \sqrt[3]{{(8{x^6})}} + 5\) (A1)
\(g(x) = 2{x^2} + 5\) A1 N2
Question
Let \(f(x) = 8x + 3\) and \(g(x) = 4x\), for \(x \in \mathbb{R}\).
Write down \(g(2)\).
Find \((f \circ g)(x)\).
Find \({f^{ – 1}}(x)\).
Answer/Explanation
Markscheme
\(g(2) = 8\) A1 N1
[1 mark]
attempt to form composite (in any order) (M1)
eg\(\,\,\,\,\,\)\(f(4x),{\text{ }}4 \times (8x + 3)\)
\((f \circ g)(x) = 32x + 3\) A1 N2
[2 marks]
interchanging \(x\) and \(y\) (may be seen at any time) (M1)
eg\(\,\,\,\,\,\)\(x = 8y + 3\)
\({f^{ – 1}}(x) = \frac{{x – 3}}{8}\,\,\,\,\,\left( {{\text{accept }}\frac{{x – 3}}{8},{\text{ }}y = \frac{{x – 3}}{8}} \right)\) A1 N2
[2 marks]
Question
Let \(f(x) = 6x\sqrt {1 – {x^2}} \), for \( – 1 \leqslant x \leqslant 1\), and \(g(x) = \cos (x)\), for \(0 \leqslant x \leqslant \pi \).
Let \(h(x) = (f \circ g)(x)\).
Write \(h(x)\) in the form \(a\sin (bx)\), where \(a,{\text{ }}b \in \mathbb{Z}\).
Hence find the range of \(h\).
Answer/Explanation
Markscheme
attempt to form composite in any order (M1)
eg\(\,\,\,\,\,\)\(f\left( {g(x)} \right),{\text{ }}\cos \left( {6x\sqrt {1 – {x^2}} } \right)\)
correct working (A1)
eg\(\,\,\,\,\,\)\(6\cos x\sqrt {1 – {{\cos }^2}x} \)
correct application of Pythagorean identity (do not accept \({\sin ^2}x + {\cos ^2}x = 1\)) (A1)
eg\(\,\,\,\,\,\)\({\sin ^2}x = 1 – {\cos ^2}x,{\text{ }}6\cos x\sin x,{\text{ }}6\cos x \left| \sin x\right|\)
valid approach (do not accept \(2\sin x\cos x = \sin 2x\)) (M1)
eg\(\,\,\,\,\,\)\(3(2\cos x\sin x)\)
\(h(x) = 3\sin 2x\) A1 N3
[5 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)amplitude \( = 3\), sketch with max and min \(y\)-values labelled, \( – 3 < y < 3\)
correct range A1 N2
eg\(\,\,\,\,\,\)\( – 3 \leqslant y \leqslant 3\), \([ – 3,{\text{ }}3]\) from \( – 3\) to 3
Note: Do not award A1 for \( – 3 < y < 3\) or for “between \( – 3\) and 3”.
[2 marks]
Question
Let \(f(x) = 5x\) and \(g(x) = {x^2} + 1\), for \(x \in \mathbb{R}\).
Find \({f^{ – 1}}(x)\).
Find \((f \circ g)(7)\).
Answer/Explanation
Markscheme
interchanging \(x\) and \(x\) (M1)
eg\(\,\,\,\,\,\)\(x = 5y\)
\({f^{ – 1}}\left( x \right) = \frac{x}{5}\) A1 N2
[2 marks]
METHOD 1
attempt to substitute 7 into \(g(x)\) or \(f(x)\) (M1)
eg\(\,\,\,\,\,\)\({7^2} + 1,{\text{ }}5 \times 7\)
\(g(7) = 50\) (A1)
\(f\left( {50} \right) = 250\) A1 N2
METHOD 2
attempt to form composite function (in any order) (M1)
eg\(\,\,\,\,\,\)\(5({x^2} + 1),{\text{ }}{(5x)^2} + 1\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(5 \times ({7^2} + 1)\)
\((f \circ g)(7) = 250\) A1 N2
[3 marks]
Examiners report
[N/A]
[N/A]
Question
Let \(f(x) = 1 + {{\text{e}}^{ – x}}\) and \(g(x) = 2x + b\), for \(x \in \mathbb{R}\), where \(b\) is a constant.
Find \((g \circ f)(x)\).
Given that \(\mathop {\lim }\limits_{x \to + \infty } (g \circ f)(x) = – 3\), find the value of \(b\).
Answer/Explanation
Markscheme
attempt to form composite (M1)
eg\(\,\,\,\,\,\)\(g(1 + {{\text{e}}^{ – x}})\)
correct function A1 N2
eg\(\,\,\,\,\,\)\((g \circ f)(x) = 2 + b + 2{{\text{e}}^{ – x}},{\text{ }}2(1 + {{\text{e}}^{ – x}}) + b\)
[2 marks]
evidence of \(\mathop {\lim }\limits_{x \to \infty } (2 + b + 2{{\text{e}}^{ – x}}) = 2 + b + \mathop {\lim }\limits_{x \to \infty } (2{{\text{e}}^{ – x}})\) (M1)
eg\(\,\,\,\,\,\)\(2 + b + 2{{\text{e}}^{ – \infty }}\), graph with horizontal asymptote when \(x \to \infty \)
Note: Award M0 if candidate clearly has incorrect limit, such as \(x \to 0,{\text{ }}{{\text{e}}^\infty },{\text{ }}2{{\text{e}}^0}\).
evidence that \({{\text{e}}^{ – x}} \to 0\) (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(\mathop {\lim }\limits_{x \to \infty } ({{\text{e}}^{ – x}}) = 0,{\text{ }}1 + {{\text{e}}^{ – x}} \to 1,{\text{ }}2(1) + b = – 3,{\text{ }}{{\text{e}}^{{\text{large negative number}}}} \to 0\), graph of \(y = {{\text{e}}^{ – x}}\) or
\(y = 2{{\text{e}}^{ – x}}\) with asymptote \(y = 0\), graph of composite function with asymptote \(y = – 3\)
correct working (A1)
eg\(\,\,\,\,\,\)\(2 + b = – 3\)
\(b = – 5\) A1 N2
[4 marks]
Examiners report
[N/A]
[N/A]
Question
Consider a function \(f\). The line L1 with equation \(y = 3x + 1\) is a tangent to the graph of \(f\) when \(x = 2\)
Let \(g\left( x \right) = f\left( {{x^2} + 1} \right)\) and P be the point on the graph of \(g\) where \(x = 1\).
Write down \(f’\left( 2 \right)\).
Find \(f\left( 2 \right)\).
Show that the graph of g has a gradient of 6 at P.
Let L2 be the tangent to the graph of g at P. L1 intersects L2 at the point Q.
Find the y-coordinate of Q.
Answer/Explanation
Markscheme
recognize that \(f’\left( x \right)\) is the gradient of the tangent at \(x\) (M1)
eg \(f’\left( x \right) = m\)
\(f’\left( 2 \right) = 3\) (accept m = 3) A1 N2
[2 marks]
recognize that \(f\left( 2 \right) = y\left( 2 \right)\) (M1)
eg \(f\left( 2 \right) = 3 \times 2 + 1\)
\(f\left( 2 \right) = 7\) A1 N2
[2 marks]
recognize that the gradient of the graph of g is \(g’\left( x \right)\) (M1)
choosing chain rule to find \(g’\left( x \right)\) (M1)
eg \(\frac{{{\text{d}}y}}{{{\text{d}}u}} \times \frac{{{\text{d}}u}}{{{\text{d}}x}},\,\,u = {x^2} + 1,\,\,u’ = 2x\)
\(g’\left( x \right) = f’\left( {{x^2} + 1} \right) \times 2x\) A2
\(g’\left( 1 \right) = 3 \times 2\) A1
\(g’\left( 1 \right) = 6\) AG N0
[5 marks]
at Q, L1 = L2 (seen anywhere) (M1)
recognize that the gradient of L2 is g’(1) (seen anywhere) (M1)
eg m = 6
finding g (1) (seen anywhere) (A1)
eg \(g\left( 1 \right) = f\left( 2 \right),\,\,g\left( 1 \right) = 7\)
attempt to substitute gradient and/or coordinates into equation of a straight line M1
eg \(y – g\left( 1 \right) = 6\left( {x – 1} \right),\,\,y – 1 = g’\left( 1 \right)\left( {x – 7} \right),\,\,7 = 6\left( 1 \right) + {\text{b}}\)
correct equation for L2
eg \(y – 7 = 6\left( {x – 1} \right),\,\,y = 6x + 1\) A1
correct working to find Q (A1)
eg same y-intercept, \(3x = 0\)
\(y = 1\) A1 N2
[7 marks]