Question:
The function f is defined by \(f(x)= \frac{4x+1}{x+4},\) where x ∈ R, x ≠ -4 .
(a) For the graph of f
(i) write down the equation of the vertical asymptote;
(ii) find the equation of the horizontal asymptote.
(b) (i) Find f -1(x).
(ii) Using an algebraic approach, show that the graph of f -1 is obtained by a reflection of the graph of f in the y-axis followed by a reflection in the x-axis.\
The graphs of f and f -1 intersect at x = p and x = q, where p < q.
(c) (i) Find the value of p and the value of q.
(ii) Hence, find the area enclosed by the graph of f and the graph of f -1.
Answer/Explanation
Ans:
(a) (i) x =−4
(ii) attempt to substitute into \(\frac{a}{c}\) OR table with large values of x OR sketch of f showing asymptotic behaviour
y = 4
(b) (i) \(y=\frac{4x+1}{x+4},\)
attempt to interchange x and y (seen anywhere) 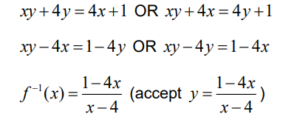
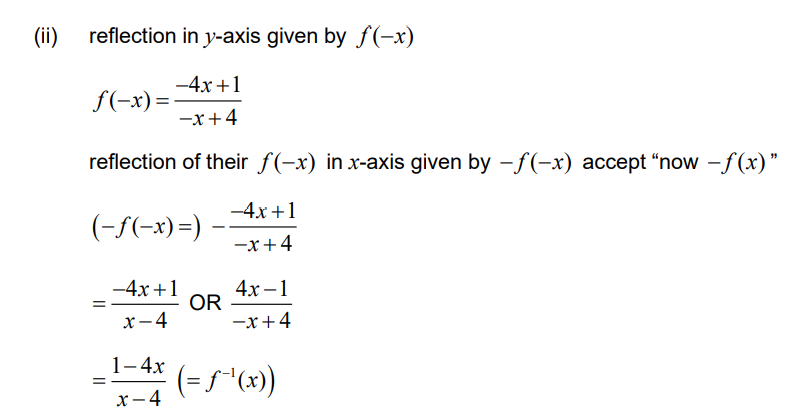
Note: If the candidate attempts to show the result using a particular coordinate on the graph of f rather than a general coordinate on the graph of f, where appropriate, award marks as follows:
M0A0 for eg (2,3) → (- 2,3)
M0A0 for ( -2,3) → ( -2, -3)
(c) (i) attempt to solve f(x) = f-1 (x) using graph or algebraically
p = −1 AND q =1
Note: Award (M1)A0 if only one correct value seen.
(ii) attempt to set up an integral to find area between f and f−1
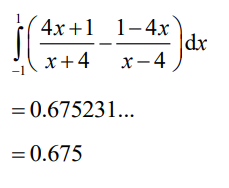
Question
A rock falls off the top of a cliff. Let \(h\) be its height above ground in metres, after \(t\) seconds.
The table below gives values of \(h\) and \(t\) .

Jane thinks that the function \(f(t) = – 0.25{t^3} – 2.32{t^2} + 1.93t + 106\) is a suitable model for the data. Use Jane’s model to
(i) write down the height of the cliff;
(ii) find the height of the rock after 4.5 seconds;
(iii) find after how many seconds the height of the rock is \(30{\text{ m}}\).
Kevin thinks that the function \(g(t) = – 5.2{t^2} + 9.5t + 100\) is a better model for the data. Use Kevin’s model to find when the rock hits the ground.
(i) On graph paper, using a scale of 1 cm to 1 second, and 1 cm to 10 m, plot the data given in the table.
(ii) By comparing the graphs of f and g with the plotted data, explain which function is a better model for the height of the falling rock.
Answer/Explanation
Markscheme
(i) \(106{\text{ m}}\) A1 N1
(ii) substitute \(t = 4.5\) M1
\(h = 44.9{\text{ m}}\) A1 N2
(iii) set up suitable equation M1
e.g. \(f(t) = 30\)
\(t = 4.91\) A1 N1
[5 marks]
recognizing that height is 0 A1
set up suitable equation M1
e.g. \(g(t) = 0\)
\(t = 5.39{\text{ secs}}\) A1 N2
[3 marks]
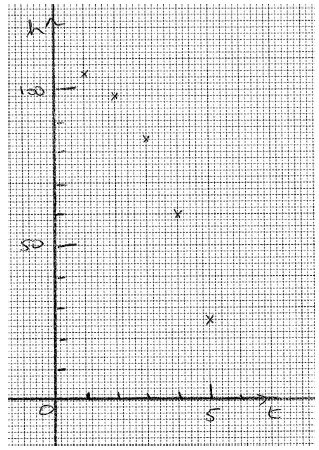 A1A2 N3
A1A2 N3
Note: Award A1 for correct scales on axes, A2 for 5 correct points, A1 for 3 or 4 correct points.
(ii) Jane’s function, with 2 valid reasons A1R1R1 N3
e.g. Jane’s passes very close to all the points, Kevin’s has the rock clearly going up initially – not possible if rock falls
Note: Although Jane’s also goes up initially, it only goes up very slightly, and so is the better model.
[6 marks]
Question
Let \(f(x) = {x^3} – 4x + 1\) .
Expand \({(x + h)^3}\) .
Use the formula \(f'(x) = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h) – f(x)}}{h}\) to show that the derivative of \(f(x)\) is \(3{x^2} – 4\) .
The tangent to the curve of f at the point \({\text{P}}(1{\text{, }} – 2)\) is parallel to the tangent at a point Q. Find the coordinates of Q.
The graph of f is decreasing for \(p < x < q\) . Find the value of p and of q.
Write down the range of values for the gradient of \(f\) .
Answer/Explanation
Markscheme
attempt to expand (M1)
\({(x + h)^3} = {x^3} + 3{x^2}h + 3x{h^2} + {h^3}\) A1 N2
[2 marks]
evidence of substituting \(x + h\) (M1)
correct substitution A1
e.g. \(f'(x) = \mathop {\lim }\limits_{h \to 0} \frac{{{{(x + h)}^3} – 4(x + h) + 1 – ({x^3} – 4x + 1)}}{h}\)
simplifying A1
e.g. \(\frac{{({x^3} + 3{x^2}h + 3x{h^2} + {h^3} – 4x – 4h + 1 – {x^3} + 4x – 1)}}{h}\)
factoring out h A1
e.g. \(\frac{{h(3{x^2} + 3xh + {h^2} – 4)}}{h}\)
\(f'(x) = 3{x^2} – 4\) AG N0
[4 marks]
\(f'(1) = – 1\) (A1)
setting up an appropriate equation M1
e.g. \(3{x^2} – 4 = – 1\)
at Q, \(x = – 1,y = 4\) (Q is \(( – 1{\text{, }}4)\)) A1 A1
[4 marks]
recognizing that f is decreasing when \(f'(x) < 0\) R1
correct values for p and q (but do not accept \(p = 1.15{\text{, }}q = – 1.15\) ) A1A1 N1N1
e.g. \(p = – 1.15{\text{, }}q = 1.15\) ; \( \pm \frac{2}{{\sqrt 3 }}\) ; an interval such as \( – 1.15 \le x \le 1.15\)
[3 marks]
\(f'(x) \ge – 4\) , \(y \ge – 4\) , \(\left[ { – 4,\infty } \right[\) A2 N2
[2 marks]
Question
Let \(f(x) = {x^2} + 2x + 1\) and \(g(x) = x – 5\), for \(x \in \mathbb{R}\).
Find \(f(8)\).
Find \((g \circ f)(x)\).
Solve \((g \circ f)(x) = 0\).
Answer/Explanation
Markscheme
attempt to substitute \(x = 8\) (M1)
eg\(\,\,\,\,\,\)\({8^2} + 2 \times 8 + 1\)
\(f(8) = 81\) A1 N2
[2 marks]
attempt to form composition (in any order) (M1)
eg\(\,\,\,\,\,\)\(f(x – 5),{\text{ }}g\left( {f(x)} \right),{\text{ }}\left( {{x^2} + 2x + 1} \right) – 5\)
\((g \circ f)(x) = {x^2} + 2x – 4\) A1 N2
[2 marks]
valid approach (M1)
eg \(x = \frac{{ – 2 \pm \sqrt {20} }}{2}\), 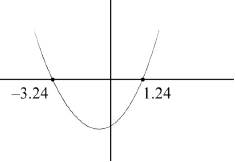
\(1.23606,{\text{ }} – 3.23606\)
\(x = 1.24,{\text{ }}x = – 3.24\) A1A1 N3
[3 marks]
Question
Let \(f(x) = 3x\) , \(g(x) = 2x – 5\) and \(h(x) = (f \circ g)(x)\) .
Find \(h(x)\) .
Find \({h^{ – 1}}(x)\) .
Answer/Explanation
Markscheme
attempt to form composite (M1)
e.g. \(f(2x – 5)\)
\(h(x) = 6x – 15\) A1 N2
[2 marks]
interchanging x and y (M1)
evidence of correct manipulation (A1)
e.g. \(y + 15 = 6x\) , \(\frac{x}{6} = y – \frac{5}{2}\)
\({h^{ – 1}}(x) = \frac{{x + 15}}{6}\) A1 N3
[3 marks]
Question
Let \(f(x) = \ln x\) and \(g(x) = 3 + \ln \left( {\frac{x}{2}} \right)\), for \(x > 0\).
The graph of \(g\) can be obtained from the graph of \(f\) by two transformations:
\[\begin{array}{*{20}{l}} {{\text{a horizontal stretch of scale factor }}q{\text{ followed by}}} \\ {{\text{a translation of }}\left( {\begin{array}{*{20}{c}} h \\ k \end{array}} \right).} \end{array}\]
Let \(h(x) = g(x) \times \cos (0.1x)\), for \(0 < x < 4\). The following diagram shows the graph of \(h\) and the line \(y = x\).
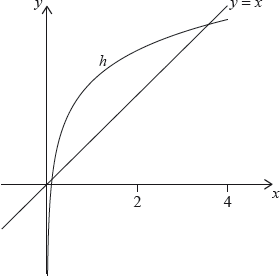
The graph of \(h\) intersects the graph of \({h^{ – 1}}\) at two points. These points have \(x\) coordinates 0.111 and 3.31 correct to three significant figures.
Write down the value of \(q\);
Write down the value of \(h\);
Write down the value of \(k\).
Find \(\int_{0.111}^{3.31} {\left( {h(x) – x} \right){\text{d}}x} \).
Hence, find the area of the region enclosed by the graphs of \(h\) and \({h^{ – 1}}\).
Let \(d\) be the vertical distance from a point on the graph of \(h\) to the line \(y = x\). There is a point \({\text{P}}(a,{\text{ }}b)\) on the graph of \(h\) where \(d\) is a maximum.
Find the coordinates of P, where \(0.111 < a < 3.31\).
Answer/Explanation
Markscheme
\(q = 2\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(h = 0\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
\(k = 3\) A1 N1
Note: Accept \(q = 1\), \(h = 0\), and \(k = 3 – \ln (2)\), 2.31 as candidate may have rewritten \(g(x)\) as equal to \(3 + \ln (x) – \ln (2)\).
[1 mark]
2.72409
2.72 A2 N2
[2 marks]
recognizing area between \(y = x\) and \(h\) equals 2.72 (M1)
eg\(\,\,\,\,\,\)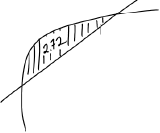
recognizing graphs of \(h\) and \({h^{ – 1}}\) are reflections of each other in \(y = x\) (M1)
eg\(\,\,\,\,\,\)area between \(y = x\) and \(h\) equals between \(y = x\) and \({h^{ – 1}}\)
\(2 \times 2.72\int_{0.111}^{3.31} {\left( {x – {h^{ – 1}}(x)} \right){\text{d}}x = 2.72} \)
5.44819
5.45 A1 N3
[??? marks]
valid attempt to find \(d\) (M1)
eg\(\,\,\,\,\,\)difference in \(y\)-coordinates, \(d = h(x) – x\)
correct expression for \(d\) (A1)
eg\(\,\,\,\,\,\)\(\left( {\ln \frac{1}{2}x + 3} \right)(\cos 0.1x) – x\)
valid approach to find when \(d\) is a maximum (M1)
eg\(\,\,\,\,\,\)max on sketch of \(d\), attempt to solve \(d’ = 0\)
0.973679
\(x = 0.974\) A2 N4
substituting their \(x\) value into \(h(x)\) (M1)
2.26938
\(y = 2.27\) A1 N2
[7 marks]
