Download IITian Academy App for accessing Online Mock Tests and More..
Question
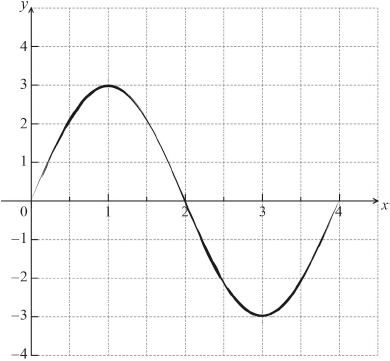
Let \(f(x) = 3\sin \left( {\frac{\pi }{2}x} \right)\), for \(0 \leqslant x \leqslant 4\).
(i) Write down the amplitude of \(f\).
(ii) Find the period of \(f\).
On the following grid sketch the graph of \(f\).
Answer/Explanation
Markscheme
(i) 3 A1 N1
(ii) valid attempt to find the period (M1)
eg\(\,\,\,\,\,\)\(\frac{{2\pi }}{b},{\text{ }}\frac{{2\pi }}{{\frac{\pi }{2}}}\)
period \( = 4\) A1 N2
[3 marks]
A1A1A1A1 N4
[4 marks]
Examiners report
Almost all candidates correctly stated the amplitude but then had difficulty finding the correct period. Few students faced problems in sketching the graph of the given function, even if they had found the wrong period, thus indicating a lack of understanding of the term ‘period’ in part a(ii). Most sketches were good although care should be taken to observe the given domain and to draw a neat curve.
Almost all candidates correctly stated the amplitude but then had difficulty finding the correct period. Few students faced problems in sketching the graph of the given function, even if they had found the wrong period, thus indicating a lack of understanding of the term ‘period’ in part a(ii). Most sketches were good although care should be taken to observe the given domain and to draw a neat curve.
Question
The following diagram shows the graph of a function \(f\), with domain \( – 2 \leqslant x \leqslant 4\).
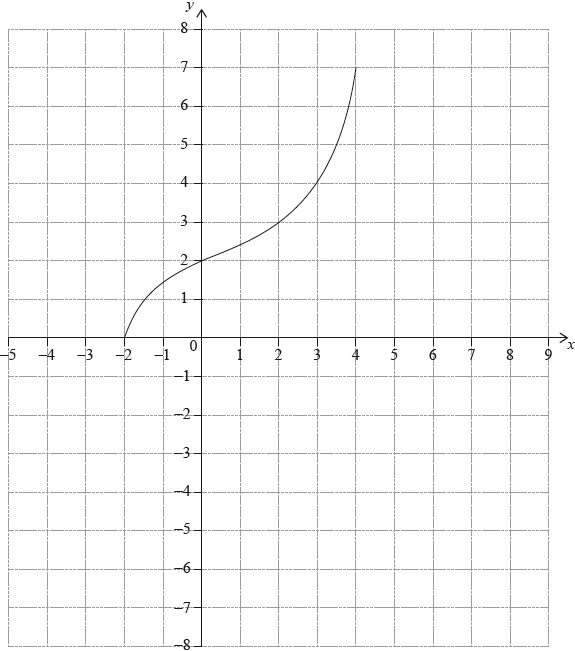
The points \(( – 2,{\text{ }}0)\) and \((4,{\text{ }}7)\) lie on the graph of \(f\).
Write down the range of \(f\).
Write down \(f(2)\);
Write down \({f^{ – 1}}(2)\).
On the grid, sketch the graph of \({f^{ – 1}}\).
Answer/Explanation
Markscheme
correct range (do not accept \(0 \leqslant x \leqslant 7\)) A1 N1
eg\(\,\,\,\,\,\)\([0,{\text{ }}7],{\text{ }}0 \leqslant y \leqslant 7\)
[1 mark]
\(f(2) = 3\) A1 N1
[1 mark]
\({f^{ – 1}}(2) = 0\) A1 N1
[1 mark]
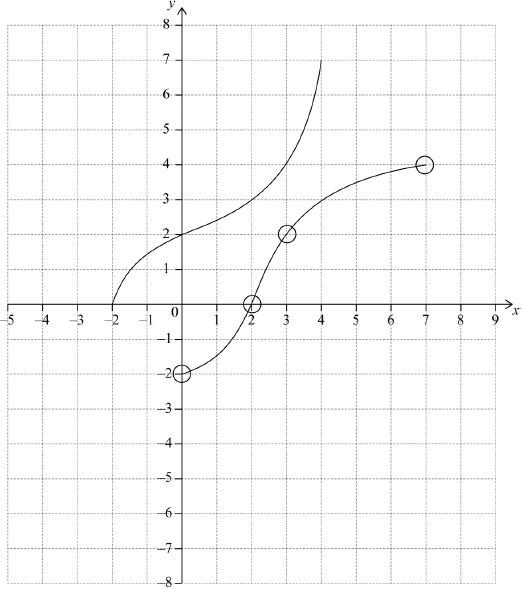A1A1A1 N3
Notes: Award A1 for both end points within circles,
A1 for images of \((2,{\text{ }}3)\) and \((0,{\text{ }}2)\) within circles,
A1 for approximately correct reflection in \(y = x\), concave up then concave down shape (do not accept line segments).
[3 marks]
Question
Consider a function f (x) , for −2 ≤ x ≤ 2 . The following diagram shows the graph of f.
Write down the value of f (0).
Write down the value of f −1 (1).
Write down the range of f −1.
On the grid above, sketch the graph of f −1.
Answer/Explanation
Markscheme
\(f\left( 0 \right) = – \frac{1}{2}\) A1 N1
[1 mark]
f −1 (1) = 2 A1 N1
[1 mark]
−2 ≤ y ≤ 2, y∈ [−2, 2] (accept −2 ≤ x ≤ 2) A1 N1
[1 mark]
A1A1A1A1 N4
Note: Award A1 for evidence of approximately correct reflection in y = x with correct curvature.
(y = x does not need to be explicitly seen)
Only if this mark is awarded, award marks as follows:
A1 for both correct invariant points in circles,
A1 for the three other points in circles,
A1 for correct domain.
[4 marks]
Question
The following diagram shows the graph of a function \(f\), for −4 ≤ x ≤ 2.
On the same axes, sketch the graph of \(f\left( { – x} \right)\).
Another function, \(g\), can be written in the form \(g\left( x \right) = a \times f\left( {x + b} \right)\). The following diagram shows the graph of \(g\).
Write down the value of a and of b.
Answer/Explanation
Markscheme
A2 N2
[2 marks]
recognizing horizontal shift/translation of 1 unit (M1)
eg b = 1, moved 1 right
recognizing vertical stretch/dilation with scale factor 2 (M1)
eg a = 2, y ×(−2)
a = −2, b = −1 A1A1 N2N2
[4 marks]
Question
Consider a function \(f\). The line L1 with equation \(y = 3x + 1\) is a tangent to the graph of \(f\) when \(x = 2\)
Let \(g\left( x \right) = f\left( {{x^2} + 1} \right)\) and P be the point on the graph of \(g\) where \(x = 1\).
Write down \(f’\left( 2 \right)\).
Find \(f\left( 2 \right)\).
Show that the graph of g has a gradient of 6 at P.
Let L2 be the tangent to the graph of g at P. L1 intersects L2 at the point Q.
Find the y-coordinate of Q.
Answer/Explanation
Markscheme
recognize that \(f’\left( x \right)\) is the gradient of the tangent at \(x\) (M1)
eg \(f’\left( x \right) = m\)
\(f’\left( 2 \right) = 3\) (accept m = 3) A1 N2
[2 marks]
recognize that \(f\left( 2 \right) = y\left( 2 \right)\) (M1)
eg \(f\left( 2 \right) = 3 \times 2 + 1\)
\(f\left( 2 \right) = 7\) A1 N2
[2 marks]
recognize that the gradient of the graph of g is \(g’\left( x \right)\) (M1)
choosing chain rule to find \(g’\left( x \right)\) (M1)
eg \(\frac{{{\text{d}}y}}{{{\text{d}}u}} \times \frac{{{\text{d}}u}}{{{\text{d}}x}},\,\,u = {x^2} + 1,\,\,u’ = 2x\)
\(g’\left( x \right) = f’\left( {{x^2} + 1} \right) \times 2x\) A2
\(g’\left( 1 \right) = 3 \times 2\) A1
\(g’\left( 1 \right) = 6\) AG N0
[5 marks]
at Q, L1 = L2 (seen anywhere) (M1)
recognize that the gradient of L2 is g’(1) (seen anywhere) (M1)
eg m = 6
finding g (1) (seen anywhere) (A1)
eg \(g\left( 1 \right) = f\left( 2 \right),\,\,g\left( 1 \right) = 7\)
attempt to substitute gradient and/or coordinates into equation of a straight line M1
eg \(y – g\left( 1 \right) = 6\left( {x – 1} \right),\,\,y – 1 = g’\left( 1 \right)\left( {x – 7} \right),\,\,7 = 6\left( 1 \right) + {\text{b}}\)
correct equation for L2
eg \(y – 7 = 6\left( {x – 1} \right),\,\,y = 6x + 1\) A1
correct working to find Q (A1)
eg same y-intercept, \(3x = 0\)
\(y = 1\) A1 N2
[7 marks]