Question
The diagram shows two concentric circles with centre O.
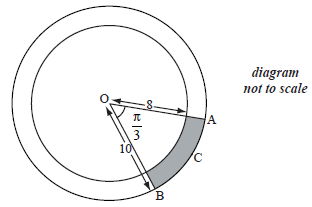
The radius of the smaller circle is 8 cm and the radius of the larger circle is 10 cm.
Points A, B and C are on the circumference of the larger circle such that \({\rm{A}}\widehat {\rm{O}}{\rm{B}}\) is \(\frac{\pi }{3}\) radians.
Find the length of the arc ACB .
Find the area of the shaded region.
Answer/Explanation
Markscheme
correct substitution in \(l = r\theta \) (A1)
e.g. \(10 \times \frac{\pi }{3}\) , \(\frac{1}{6} \times 2\pi \times 10\)
arc length \( = \frac{{20\pi }}{6}\) \(\left( { = \frac{{10\pi }}{3}} \right)\) A1 N2
[2 marks]
area of large sector \( = \frac{1}{2} \times {10^2} \times \frac{\pi }{3}\) \(\left( { = \frac{{100\pi }}{6}} \right)\) (A1)
area of small sector \( = \frac{1}{2} \times {8^2} \times \frac{\pi }{3}\) \(\left( { = \frac{{64\pi }}{6}} \right)\) (A1)
evidence of valid approach (seen anywhere) M1
e.g. subtracting areas of two sectors, \(\frac{1}{2} \times \frac{\pi }{3}({10^2} – {8^2})\)
area shaded \( = 6\pi \) (accept \(\frac{{36\pi }}{6}\) , etc.) A1 N3
[4 marks]
Question
The following diagram shows a circle with centre \(O\) and a radius of \(10\) cm. Points \(A\), \(B\) and \(C\) lie on the circle.
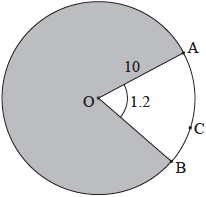
Angle \(AOB\) is \(1.2\) radians.
Find the length of \({\text{arc ACB}}\).
Find the perimeter of the shaded region.
Answer/Explanation
Markscheme
correct substitution (A1)
eg\(\;\;\;10(1.2)\)
\(ACB\) is \(12{\text{ (cm)}}\) A1 N2
[2 marks]
valid approach to find major arc (M1)
eg\(\;\;\;\)circumference \( – {\text{AB}}\), major angle \({\text{AOB}} \times {\text{radius}}\)
correct working for arc length (A1)
eg\(\;\;\;2\pi (10) – 12,{\text{ }}10(2 \times 3.142 – 1.2),{\text{ }}2\pi (10) – 12 + 20\)
perimeter is \(20\pi + 8\;\;\;( = 70.8){\text{ (cm)}}\) A1 N2
[3 marks]
Total [5 marks]
Question
The following diagram shows a triangle ABC and a sector BDC of a circle with centre B and radius 6 cm. The points A , B and D are on the same line.
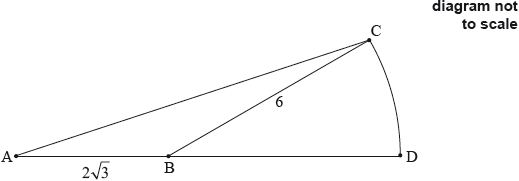
\({\text{AB}} = 2\sqrt 3 {\text{ cm, BC}} = 6{\text{ cm, area of triangle ABC}} = 3\sqrt 3{\text{ c}}{{\text{m}}^{\text{2}}}{\rm{, A\hat BC}}\) is obtuse.
Find \({\rm{A\hat BC}}\).
Find the exact area of the sector BDC.
Answer/Explanation
Markscheme
METHOD 1
correct substitution into formula for area of triangle (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}(6)\left( {2\sqrt 3 } \right)\sin B,{\text{ }}6\sqrt 3 \sin B,{\text{ }}\frac{1}{2}(6)\left( {2\sqrt 3 } \right)\sin B = 3\sqrt 3 \)
correct working (A1)
eg\(\,\,\,\,\,\)\(6\sqrt 3 \sin B = 3\sqrt 3 ,{\text{ }}\sin B = \frac{{3\sqrt 3 }}{{\frac{1}{2}(6)2\sqrt 3 }}\)
\(\sin B = \frac{1}{2}\) (A1)
\(\frac{\pi }{6}(30^\circ )\) (A1)
\({\rm{A\hat BC}} = \frac{{5\pi }}{6}(150^\circ )\) A1 N3
METHOD 2
(using height of triangle ABC by drawing perpendicular segment from C to AD)
correct substitution into formula for area of triangle (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}\left( {2\sqrt 3 } \right)(h) = 3\sqrt 3 ,{\text{ }}h\sqrt 3 \)
correct working (A1)
eg\(\,\,\,\,\,\)\(h\sqrt 3 = 3\sqrt 3 \)
height of triangle is 3 A1
\({\rm{C\hat BD}} = \frac{\pi }{6}(30^\circ )\) (A1)
\({\rm{A\hat BC}} = \frac{{5\pi }}{6}(150^\circ )\) A1 N3
[5 marks]
recognizing supplementary angle (M1)
eg\(\,\,\,\,\,\)\({\rm{C\hat BD}} = \frac{\pi }{6},{\text{ sector}} = \frac{1}{2}(180 – {\rm{A\hat BC)(}}{{\text{6}}^2})\)
correct substitution into formula for area of sector (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2} \times \frac{\pi }{6} \times {6^2},{\text{ }}\pi ({6^2})\left( {\frac{{30}}{{360}}} \right)\)
\({\text{area}} = 3\pi {\text{ }}({\text{c}}{{\text{m}}^2})\) A1 N2
[3 marks]
Question
The following diagram shows triangle ABC, with \({\text{AB}} = 3{\text{ cm}}\), \({\text{BC}} = 8{\text{ cm}}\), and \({\rm{A\hat BC = }}\frac{\pi }{3}\).
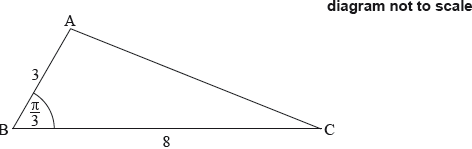
Show that \({\text{AC}} = 7{\text{ cm}}\).
The shape in the following diagram is formed by adding a semicircle with diameter [AC] to the triangle.
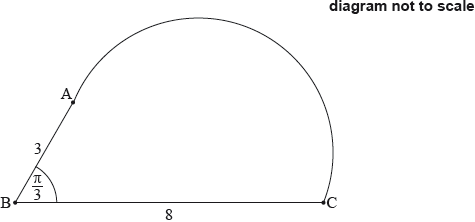
Find the exact perimeter of this shape.
Answer/Explanation
Markscheme
evidence of choosing the cosine rule (M1)
eg\(\,\,\,\,\,\)\({c^2} = {a^2} + {b^2} – ab\cos C\)
correct substitution into RHS of cosine rule (A1)
eg\(\,\,\,\,\,\)\({3^2} + {8^2} – 2 \times 3 \times 8 \times \cos \frac{\pi }{3}\)
evidence of correct value for \(\cos \frac{\pi }{3}\) (may be seen anywhere, including in cosine rule) A1
eg\(\,\,\,\,\,\)\(\cos \frac{\pi }{3} = \frac{1}{2},{\text{ A}}{{\text{C}}^2} = 9 + 64 – \left( {48 \times \frac{1}{2}} \right),{\text{ }}9 + 64 – 24\)
correct working clearly leading to answer A1
eg\(\,\,\,\,\,\)\({\text{A}}{{\text{C}}^2} = 49,{\text{ }}b = \sqrt {49} \)
\({\text{AC}} = 7{\text{ (cm)}}\) AG N0
Note: Award no marks if the only working seen is \({\text{A}}{{\text{C}}^2} = 49\) or \({\text{AC}} = \sqrt {49} \) (or similar).
[4 marks]
correct substitution for semicircle (A1)
eg\(\,\,\,\,\,\)\({\text{semicircle}} = \frac{1}{2}(2\pi \times 3.5),{\text{ }}\frac{1}{2} \times \pi \times 7,{\text{ }}3.5\pi \)
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\({\text{perimeter}} = {\text{AB}} + {\text{BC}} + {\text{semicircle, }}3 + 8 + \left( {\frac{1}{2} \times 2 \times \pi \times \frac{7}{2}} \right),{\text{ }}8 + 3 + 3.5\pi \)
\(11 + \frac{7}{2}\pi {\text{ }}( = 3.5\pi + 11){\text{ (cm)}}\) A1 N2
[3 marks]
Question
The following diagram shows a circle with centre O and radius r cm.
The points A and B lie on the circumference of the circle, and \({\text{A}}\mathop {\text{O}}\limits^ \wedge {\text{B}}\) = θ. The area of the shaded sector AOB is 12 cm2 and the length of arc AB is 6 cm.
Find the value of r.
Answer/Explanation
Markscheme
evidence of correctly substituting into circle formula (may be seen later) A1A1
eg \(\frac{1}{2}\theta {r^2} = 12,\,\,r\theta = 6\)
attempt to eliminate one variable (M1)
eg \(r = \frac{6}{\theta },\,\,\theta = \frac{1}{r},\,\,\frac{{\frac{1}{2}\theta {r^2}}}{{r\theta }} = \frac{{12}}{6}\)
correct elimination (A1)
eg \(\frac{1}{2} \times \frac{6}{r} \times {r^2} = 12,\,\,\frac{1}{2}\theta \times {\left( {\frac{6}{\theta }} \right)^2} = 12,\,\,A = \frac{1}{2} \times {r^2} \times \frac{l}{r},\,\,\frac{{{r^2}}}{{2r}} = 2\)
correct equation (A1)
eg \(\frac{1}{2} \times 6r = 12,\,\,\frac{1}{2} \times \frac{{36}}{\theta } = 12,\,\,12 = \frac{1}{2} \times {r^2} \times \frac{6}{r}\)
correct working (A1)
eg \(3r = 12,\,\,\frac{{18}}{\theta } = 12,\,\,\frac{r}{2} = 2,\,\,24 = 6r\)
r = 4 (cm) A1 N2
[7 marks]
