Download IITian Academy App for accessing Online Mock Tests and More..
Question
The following graph shows the depth of water, y metres , at a point P, during one day. The time t is given in hours, from midnight to noon.
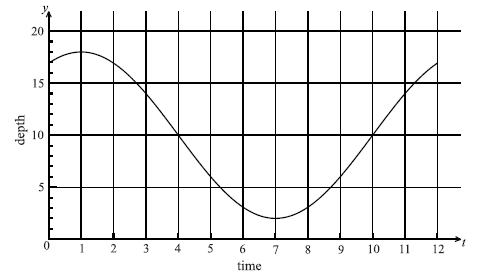
Use the graph to write down an estimate of the value of t when
(i) the depth of water is minimum;
(ii) the depth of water is maximum;
(iii) the depth of the water is increasing most rapidly.
The depth of water can be modelled by the function \(y = \cos A(B(t – 1)) + C\) .
(i) Show that \(A = 8\) .
(ii) Write down the value of C.
(iii) Find the value of B.
A sailor knows that he cannot sail past P when the depth of the water is less than 12 m . Calculate the values of t between which he cannot sail past P.
Answer/Explanation
Markscheme
(i) 7 A1 N1
(ii) 1 A1 N1
(iii) 10 A1 N1
[3 marks]
(i) evidence of appropriate approach M1
e.g. \(A = \frac{{18 – 2}}{2}\)
\(A = 8\) AG N0
(ii) \(C = 10\) A2 N2
(iii) METHOD 1
\({\text{period}} = 12\) (A1)
evidence of using \(B \times {\rm{period}} = 2\pi \) (accept \(360^\circ \) ) (M1)
e.g. \(12 = \frac{{2\pi }}{B}\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
METHOD 2
evidence of substituting (M1)
e.g. \(10 = 8\cos 3B + 10\)
simplifying (A1)
e.g. \(\cos 3B = 0\) \(\left( {3B = \frac{\pi }{2}} \right)\)
\(B = \frac{\pi }{6}\) (accept 0.524 or 30) A1 N3
[6 marks]
correct answers A1A1
e.g. \(t = 3.52\) , \(t = 10.5\) , between 03:31 and 10:29 (accept 10:30) N2
[2 marks]
Question
Let \(f(x) = 3\sin x + 4\cos x\) , for \( – 2\pi \le x \le 2\pi \) .
Sketch the graph of f .
Write down
(i) the amplitude;
(ii) the period;
(iii) the x-intercept that lies between \( – \frac{\pi }{2}\) and 0.
Hence write \(f(x)\) in the form \(p\sin (qx + r)\) .
Write down one value of x such that \(f'(x) = 0\) .
Write down the two values of k for which the equation \(f(x) = k\) has exactly two solutions.
Let \(g(x) = \ln (x + 1)\) , for \(0 \le x \le \pi \) . There is a value of x, between \(0\) and \(1\), for which the gradient of f is equal to the gradient of g. Find this value of x.
Answer/Explanation
Markscheme
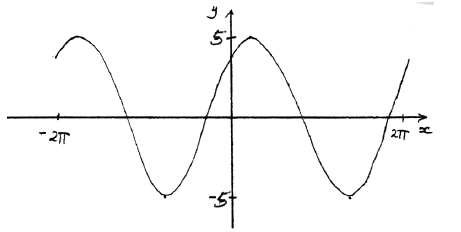A1A1A1 N3
Note: Award A1 for approximately sinusoidal shape, A1 for end points approximately correct \(( – 2\pi {\text{, }}4)\) \((2\pi {\text{, }}4)\), A1 for approximately correct position of graph, (y-intercept \((0{\text{, }}4)\), maximum to right of y-axis).
[3 marks]
(i) 5 A1 N1
(ii) \(2\pi \) (6.28) A1 N1
(iii) \( – 0.927\) A1 N1
[3 marks]
\(f(x) = 5\sin (x + 0.927)\) (accept \(p = 5\) , \(q = 1\) , \(r = 0.927\) ) A1A1A1 N3
[3 marks]
evidence of correct approach (M1)
e.g. max/min, sketch of \(f'(x)\) indicating roots
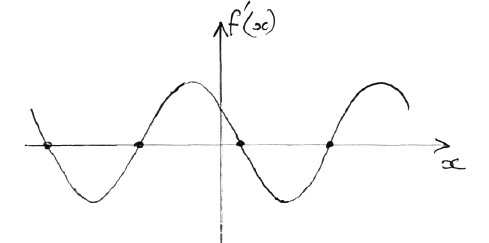
one 3 s.f. value which rounds to one of \( – 5.6\), \( – 2.5\), \(0.64\), \(3.8\) A1 N2
[2 marks]
\(k = – 5\) , \(k = 5\) A1A1 N2
[2 marks]
METHOD 1
graphical approach (but must involve derivative functions) M1
e.g.
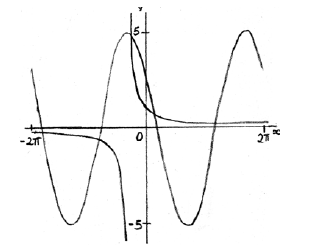
each curve A1A1
\(x = 0.511\) A2 N2
METHOD 2
\(g'(x) = \frac{1}{{x + 1}}\) A1
\(f'(x) = 3\cos x – 4\sin x\) \((5\cos (x + 0.927))\) A1
evidence of attempt to solve \(g'(x) = f'(x)\) M1
\(x = 0.511\) A2 N2
[5 marks]
Question
The graph of \(y = p\cos qx + r\) , for \( – 5 \le x \le 14\) , is shown below.
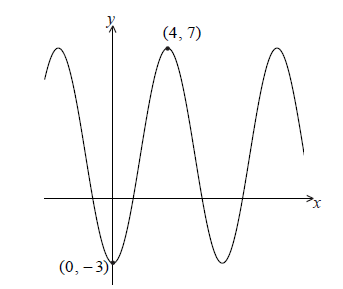
There is a minimum point at (0, −3) and a maximum point at (4, 7) .
Find the value of
(i) p ;
(ii) q ;
(iii) r.
The equation \(y = k\) has exactly two solutions. Write down the value of k.
Answer/Explanation
Markscheme
(i) evidence of finding the amplitude (M1)
e.g. \(\frac{{7 + 3}}{2}\) , amplitude \(= 5\)
\(p = – 5\) A1 N2
(ii) period \(= 8\) (A1)
\(q = 0.785\) \(\left( { = \frac{{2\pi }}{8} = \frac{\pi }{4}} \right)\) A1 N2
(iii) \(r = \frac{{7 – 3}}{2}\) (A1)
\(r = 2\) A1 N2
[6 marks]
\(k = – 3\) (accept \(y = – 3\) ) A1 N1
[1 mark]
Question
The following diagram represents a large Ferris wheel at an amusement park.
The points P, Q and R represent different positions of a seat on the wheel.
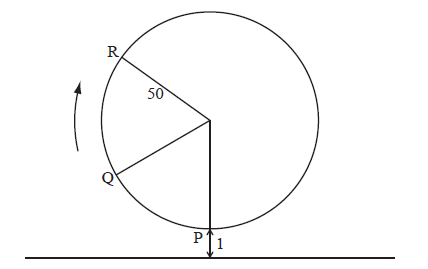
The wheel has a radius of 50 metres and rotates clockwise at a rate of one revolution every 30 minutes.
A seat starts at the lowest point P, when its height is one metre above the ground.
Find the height of a seat above the ground after 15 minutes.
After six minutes, the seat is at point Q. Find its height above the ground at Q.
The height of the seat above ground after t minutes can be modelled by the function \(h(t) = 50\sin (b(t – c)) + 51\).
Find the value of b and of c .
The height of the seat above ground after t minutes can be modelled by the function \(h(t) = 50\sin (b(t – c)) + 51\).
Hence find the value of t the first time the seat is \(96{\text{ m}}\) above the ground.
Answer/Explanation
Markscheme
valid approach (M1)
e.g. 15 mins is half way, top of the wheel, \(d + 1\)
height \( = 101\) (metres) A1 N2
[2 marks]
evidence of identifying rotation angle after 6 minutes A1
e.g. \(\frac{{2\pi }}{5}\) , \(\frac{1}{5}\) of a rotation, \({72^ \circ }\)
evidence of appropriate approach (M1)
e.g. drawing a right triangle and using cosine ratio
correct working (seen anywhere) A1
e.g. \(\cos \frac{{2\pi }}{5} = \frac{x}{{50}}\) , \(15.4(508 \ldots )\)
evidence of appropriate method M1
e.g. height \(= {\rm{radius}} + 1 – 15.45 \ldots \)
height \(= 35.5\) (metres) (accept 35.6) A1 N2
[5 marks]
METHOD 1
evidence of substituting into \(b = \frac{{2\pi }}{{{\rm{period}}}}\) (M1)
correct substitution
e.g. period = 30 minutes, \(b = \frac{{2\pi }}{{30}}\) A1
\(b = 0.209\) \(\left( {\frac{\pi }{{15}}} \right)\) A1 N2
substituting into \(h(t)\) (M1)
e.g. \(h(0) = 1\) , \(h(15) = 101\)
correct substitution A1
\(1 = 50\sin \left( { – \frac{\pi }{{15}}c} \right) + 51\)
\(c = 7.5\) A1 N2
METHOD 2
evidence of setting up a system of equations (M1)
two correct equations
e.g. \(1 = 50\sin b(0 – c) + 51\) , \(101 = 50\sin b(15 – c) + 51\) A1A1
attempt to solve simultaneously (M1)
e.g. evidence of combining two equations
\(b = 0.209\) \(\left( {\frac{\pi }{{15}}} \right)\) , \(c = 7.5\) A1A1 N2N2
[6 marks]
evidence of solving \(h(t) = 96\) (M1)
e.g. equation, graph
\(t = 12.8\) (minutes) A2 N3
[3 marks]
Question
The following diagram shows a waterwheel with a bucket. The wheel rotates at a constant rate in an anticlockwise (counter-clockwise) direction.
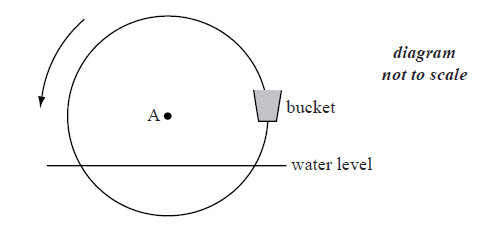
The diameter of the wheel is 8 metres. The centre of the wheel, A, is 2 metres above the water level. After t seconds, the height of the bucket above the water level is given by \(h = a\sin bt + 2\) .
Show that \(a = 4\) .
The wheel turns at a rate of one rotation every 30 seconds.
Show that \(b = \frac{\pi }{{15}}\) .
In the first rotation, there are two values of t when the bucket is descending at a rate of \(0.5{\text{ m}}{{\text{s}}^{ – 1}}\) .
Find these values of t .
In the first rotation, there are two values of t when the bucket is descending at a rate of \(0.5{\text{ m}}{{\text{s}}^{ – 1}}\) .
Determine whether the bucket is underwater at the second value of t .
Answer/Explanation
Markscheme
METHOD 1
evidence of recognizing the amplitude is the radius (M1)
e.g. amplitude is half the diameter
\(a = \frac{8}{2}\) A1
\(a = 4\) AG N0
METHOD 2
evidence of recognizing the maximum height (M1)
e.g. \(h = 6\) , \(a\sin bt + 2 = 6\)
correct reasoning
e.g. \(a\sin bt = 4\) and \(\sin bt\) has amplitude of 1 A1
\(a = 4\) AG N0
[2 marks]
METHOD 1
period = 30 (A1)
\(b = \frac{{2\pi }}{{30}}\) A1
\(b = \frac{\pi }{{15}}\) AG N0
METHOD 2
correct equation (A1)
e.g. \(2 = 4\sin 30b + 2\) , \(\sin 30b = 0\)
\(30b = 2\pi \) A1
\(b = \frac{\pi }{{15}}\) AG N0
[2 marks]
recognizing \(h'(t) = – 0.5\) (seen anywhere) R1
attempting to solve (M1)
e.g. sketch of \(h’\) , finding \(h’\)
correct work involving \(h’\) A2
e.g. sketch of \(h’\) showing intersection, \( – 0.5 = \frac{{4\pi }}{{15}}\cos \left( {\frac{\pi }{{15}}t} \right)\)
\(t = 10.6\) , \(t = 19.4\) A1A1 N3
[6 marks]
METHOD 1
valid reasoning for their conclusion (seen anywhere) R1
e.g. \(h(t) < 0\) so underwater; \(h(t) > 0\) so not underwater
evidence of substituting into h (M1)
e.g. \(h(19.4)\) , \(4\sin \frac{{19.4\pi }}{{15}} + 2\)
correct calculation A1
e.g. \(h(19.4) = – 1.19\)
correct statement A1 N0
e.g. the bucket is underwater, yes
METHOD 2
valid reasoning for their conclusion (seen anywhere) R1
e.g. \(h(t) < 0\) so underwater; \(h(t) > 0\) so not underwater
evidence of valid approach (M1)
e.g. solving \(h(t) = 0\) , graph showing region below x-axis
correct roots A1
e.g. \(17.5\), \(27.5\)
correct statement A1 N0
e.g. the bucket is underwater, yes
[4 marks]
Question
The diagram below shows a plan for a window in the shape of a trapezium.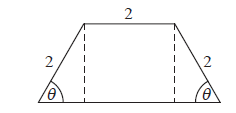
Three sides of the window are \(2{\text{ m}}\) long. The angle between the sloping sides of the window and the base is \(\theta \) , where \(0 < \theta < \frac{\pi }{2}\) .
Show that the area of the window is given by \(y = 4\sin \theta + 2\sin 2\theta \) .
Zoe wants a window to have an area of \(5{\text{ }}{{\text{m}}^2}\). Find the two possible values of \(\theta \) .
John wants two windows which have the same area A but different values of \(\theta \) .
Find all possible values for A .
Answer/Explanation
Markscheme
evidence of finding height, h (A1)
e.g. \(\sin \theta = \frac{h}{2}\) , \(2\sin \theta \)
evidence of finding base of triangle, b (A1)
e.g. \(\cos \theta = \frac{b}{2}\) , \(2\cos \theta \)
attempt to substitute valid values into a formula for the area of the window (M1)
e.g. two triangles plus rectangle, trapezium area formula
correct expression (must be in terms of \(\theta \) ) A1
e.g. \(2\left( {\frac{1}{2} \times 2\cos \theta \times 2\sin \theta } \right) + 2 \times 2\sin \theta \) , \(\frac{1}{2}(2\sin \theta )(2 + 2 + 4\cos \theta )\)
attempt to replace \(2\sin \theta \cos \theta \) by \(\sin 2\theta \) M1
e.g. \(4\sin \theta + 2(2\sin \theta \cos \theta )\)
\(y = 4\sin \theta + 2\sin 2\theta \) AG N0
[5 marks]
correct equation A1
e.g. \(y = 5\) , \(4\sin \theta + 2\sin 2\theta = 5\)
evidence of attempt to solve (M1)
e.g. a sketch, \(4\sin \theta + 2\sin \theta – 5 = 0\)
\(\theta = 0.856\) \(({49.0^ \circ })\) , \(\theta = 1.25\) \(({71.4^ \circ })\) A1A1 N3
[4 marks]
recognition that lower area value occurs at \(\theta = \frac{\pi }{2}\) (M1)
finding value of area at \(\theta = \frac{\pi }{2}\) (M1)
e.g. \(4\sin \left( {\frac{\pi }{2}} \right) + 2\sin \left( {2 \times \frac{\pi }{2}} \right)\) , draw square
\(A = 4\) (A1)
recognition that maximum value of y is needed (M1)
\(A = 5.19615 \ldots \) (A1)
\(4 < A < 5.20\) (accept \(4 < A < 5.19\) ) A2 N5
[7 marks]
Question
Consider the following circle with centre O and radius r .
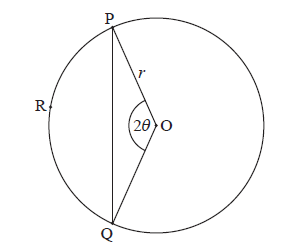
The points P, R and Q are on the circumference, \({\rm{P}}\widehat {\rm{O}}{\rm{Q}} = 2\theta \) , for \(0 < \theta < \frac{\pi }{2}\) .
Use the cosine rule to show that \({\rm{PQ}} = 2r\sin \theta \) .
Let l be the length of the arc PRQ .
Given that \(1.3{\rm{PQ}} – l = 0\) , find the value of \(\theta \) .
Consider the function \(f(\theta ) = 2.6\sin \theta – 2\theta \) , for \(0 < \theta < \frac{\pi }{2}\) .
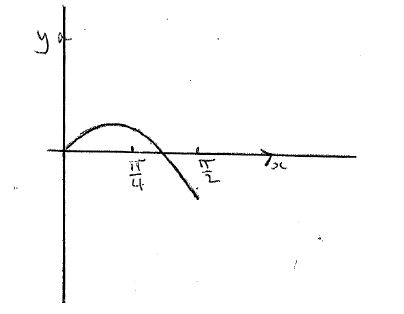
(i) Sketch the graph of f .
(ii) Write down the root of \(f(\theta ) = 0\) .
Use the graph of f to find the values of \(\theta \) for which \(l < 1.3{\rm{PQ}}\) .
Answer/Explanation
Markscheme
correct substitution into cosine rule A1
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = {r^2} + {r^2} – 2(r)(r)\cos (2\theta )\) , \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2}(\cos (2\theta ))\)
substituting \(1 – 2{\sin ^2}\theta \) for \(\cos 2\theta \) (seen anywhere) A1
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2}(1 – 2{\sin ^2}\theta )\)
working towards answer (A1)
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2} + 4{r^2}{\sin ^2}\theta \)
recognizing \(2{r^2} – 2{r^2} = 0\) (including crossing out) (seen anywhere)
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 4{r^2}{\sin ^2}\theta \) , \({\rm{PQ}} = \sqrt {4{r^2}{{\sin }^2}\theta } \)
\({\rm{PQ = 2}}r{\rm{sin}}\theta \) AG N0
[4 marks]
\({\rm{PRQ}} = r \times 2\theta \) (seen anywhere) (A1)
correct set up A1
e.g. \(1.3 \times 2r\sin \theta – r \times (2\theta ) = 0\)
attempt to eliminate r (M1)
correct equation in terms of the one variable \(\theta \) (A1)
e.g. \(1.3 \times 2\sin \theta – 2\theta = 0\)
1.221496215
\(\theta = 1.22\) (accept \(70.0^\circ \) (69.9)) A1 N3
[5 marks]
(i)
A1A1A1 N3
Note: Award A1 for approximately correct shape, A1 for x-intercept in approximately correct position, A1 for domain. Do not penalise if sketch starts at origin.
(ii) \(1.221496215\)
\(\theta = 1.22\) A1 N1
[4 marks]
evidence of appropriate approach (may be seen earlier) M2
e.g. \(2\theta < 2.6\sin \theta \) , \(0 < f(\theta )\) , showing positive part of sketch
\(0 < \theta < 1.221496215\)
\(0 < \theta = 1.22\) (accept \(\theta < 1.22\) ) A1 N1
[3 marks]
Question
A Ferris wheel with diameter \(122\) metres rotates clockwise at a constant speed. The wheel completes \(2.4\) rotations every hour. The bottom of the wheel is \(13\) metres above the ground.
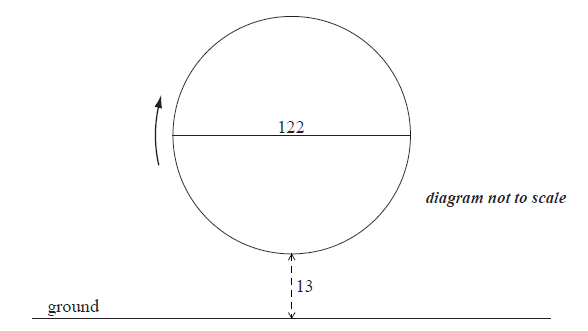
A seat starts at the bottom of the wheel.
After t minutes, the height \(h\) metres above the ground of the seat is given by\[h = 74 + a\cos bt {\rm{ .}}\]
Find the maximum height above the ground of the seat.
(i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(b) (i) Show that the period of \(h\) is \(25\) minutes.
(ii) Write down the exact value of \(b\) .
(c) Find the value of \(a\) .
(d) Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
Find the value of \(a\) .
Sketch the graph of \(h\) , for \(0 \le t \le 50\) .
In one rotation of the wheel, find the probability that a randomly selected seat is at least \(105\) metres above the ground.
Answer/Explanation
Markscheme
valid approach (M1)
eg \(13 + {\rm{diameter}}\) , \(13 + 122\)
maximum height \( = 135\) (m) A1 N2
[2 marks]
(i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(a) (i) period \( = \frac{{60}}{{2.4}}\) A1
period \( = 25\) minutes AG N0
(ii) \(b = \frac{{2\pi }}{{25}}\) \(( = 0.08\pi )\) A1 N1
[2 marks]
(b) METHOD 1
valid approach (M1)
eg \({\rm{max}} – 74\) , \(\left| a \right| = \frac{{135 – 13}}{2}\) , \(74 – 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = – 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = – 61\) A1 N2
[3 marks]
(c)
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
Total [9 marks]
METHOD 1
valid approach (M1)
eg \({\rm{max}} – 74\) , \(\left| a \right| = \frac{{135 – 13}}{2}\) , \(74 – 13\)
\(\left| a \right| = 61\) (accept \(a = 61\) ) (A1)
\(a = – 61\) A1 N2
METHOD 2
attempt to substitute valid point into equation for h (M1)
eg \(135 = 74 + a\cos \left( {\frac{{2\pi \times 12.5}}{{25}}} \right)\)
correct equation (A1)
eg \(135 = 74 + a\cos (\pi )\) , \(13 = 74 + a\)
\(a = – 61\) A1 N2
[3 marks]
A1A1A1A1 N4
Note: Award A1 for approximately correct domain, A1 for approximately correct range,
A1 for approximately correct sinusoidal shape with \(2\) cycles.
Only if this last A1 awarded, award A1 for max/min in approximately correct positions.
[4 marks]
setting up inequality (accept equation) (M1)
eg \(h > 105\) , \(105 = 74 + a\cos bt\) , sketch of graph with line \(y = 105\)
any two correct values for t (seen anywhere) A1A1
eg \(t = 8.371 \ldots \) , \(t = 16.628 \ldots \) , \(t = 33.371 \ldots \) , \(t = 41.628 \ldots \)
valid approach M1
eg \(\frac{{16.628 – 8.371}}{{25}}\) , \(\frac{{{t_1} – {t_2}}}{{25}}\) , \(\frac{{2 \times 8.257}}{{50}}\) , \(\frac{{2(12.5 – 8.371)}}{{25}}\)
\(p = 0.330\) A1 N2
[5 marks]
Question
Let \(f(x) = p\cos \left( {q(x + r)} \right) + 10\), for \(0 \leqslant x \leqslant 20\). The following diagram shows the graph of \(f\).
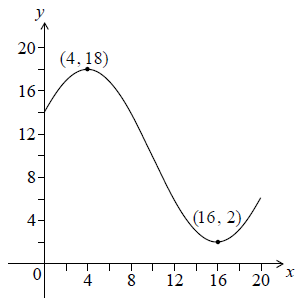
The graph has a maximum at \((4, 18)\) and a minimum at \((16, 2)\).
Write down the value of \(r\).
Find \(p\).
Find \(q\).
Solve \(f(x) = 7\).
Answer/Explanation
Markscheme
\(r = – 4\) A2 N2
Note: Award A1 for \(r = 4\).
[2 marks]
evidence of valid approach (M1)
eg \(\frac{{\max y{\text{ value — }}y{\text{ value}}}}{2}\), distance from \(y = 10\)
\(p = 8\) A1 N2
[2 marks]
valid approach (M1)
eg period is \(24\), \(\frac{{360}}{{24}}\), substitute a point into their \(f(x)\)
\(q = \frac{{2\pi }}{{24}}\left( {\frac{\pi }{{12}},{\text{ exact}}} \right)\), \(0.262\) (do not accept degrees) A1 N2
[2 marks]
valid approach (M1)
eg line on graph at \(y = 7,{\text{ }}8\cos \left( {\frac{{2\pi }}{{24}}(x – 4)} \right) + 10 = 7\)
\(x = 11.46828\)
\(x = 11.5\) (accept \((11.5, 7)\)) A1 N2
[2 marks]
Note: Do not award the final A1 if additional values are given. If an incorrect value of \(q\) leads to multiple solutions, award the final A1 only if all solutions within the domain are given.
Question
The height, \(h\) metros, of a seat on a Ferris wheel after \(t\) minutes is given by
\[h(t) = – 15\cos 1.2t + 17,{\text{ for }}t \geqslant 0{\text{.}}\]
Find the height of the seat when \(t = 0\).
The seat first reaches a height of 20 m after \(k\) minutes. Find \(k\).
Calculate the time needed for the seat to complete a full rotation, giving your answer correct to one decimal place.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(h(0),{\text{ }} – 15\cos (1.2 \times 0) + 17,{\text{ }} – 15(1) + 17\)
\(h(0) = 2{\text{ (m)}}\) A1 N2
[2 marks]
correct substitution into equation (A1)
eg\(\,\,\,\,\,\)\(20 = – 15\cos 1.2t + 17,{\text{ }} – 15\cos 1.2k = 3\)
valid attempt to solve for \(k\) (M1)
eg\(\,\,\,\,\,\)
, \(\cos 1.2k = – \frac{3}{{15}}\)
1.47679
\(k = 1.48\) A1 N2
[3 marks]
recognize the need to find the period (seen anywhere) (M1)
eg\(\,\,\,\,\,\)next \(t\) value when \(h = 20\)
correct value for period (A1)
eg\(\,\,\,\,\,\)\({\text{period}} = \frac{{2\pi }}{{1.2}},{\text{ }}5.23598,{\text{ }}6.7–1.48\)
5.2 (min) (must be 1 dp) A1 N2
[3 marks]
Question
At Grande Anse Beach the height of the water in metres is modelled by the function \(h(t) = p\cos (q \times t) + r\), where \(t\) is the number of hours after 21:00 hours on 10 December 2017. The following diagram shows the graph of \(h\) , for \(0 \leqslant t \leqslant 72\).
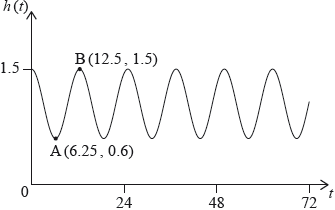
The point \({\text{A}}(6.25,{\text{ }}0.6)\) represents the first low tide and \({\text{B}}(12.5,{\text{ }}1.5)\) represents the next high tide.
How much time is there between the first low tide and the next high tide?
Find the difference in height between low tide and high tide.
Find the value of \(p\);
Find the value of \(q\);
Find the value of \(r\).
There are two high tides on 12 December 2017. At what time does the second high tide occur?
Answer/Explanation
Markscheme
attempt to find the difference of \(x\)-values of A and B (M1)
eg\(\,\,\,\,\,\)\(6.25 – 12.5{\text{ }}\)
6.25 (hours), (6 hours 15 minutes) A1 N2
[2 marks]
attempt to find the difference of \(y\)-values of A and B (M1)
eg\(\,\,\,\,\,\)\(1.5 – 0.6\)
\(0.9{\text{ (m)}}\) A1 N2
[2 marks]
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{max}} – {\text{min}}}}{2},{\text{ }}0.9 \div 2\)
\(p = 0.45\) A1 N2
[2 marks]
METHOD 1
period \( = 12.5\) (seen anywhere) (A1)
valid approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\({\text{period}} = \frac{{2\pi }}{b},{\text{ }}q = \frac{{2\pi }}{{{\text{period}}}},{\text{ }}\frac{{2\pi }}{{12.5}}\)
0.502654
\(q = \frac{{4\pi }}{{25}},{\text{ 0.503 }}\left( {{\text{or }} – \frac{{4\pi }}{{25}},{\text{ }} – 0.503} \right)\) A1 N2
METHOD 2
attempt to use a coordinate to make an equation (M1)
eg\(\,\,\,\,\,\)\(p\cos (6.25q) + r = 0.6,{\text{ }}p\cos (12.5q) + r = 1.5\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(0.45\cos (6.25q) + 1.05 = 0.6,{\text{ }}0.45\cos (12.5q) + 1.05 = 1.5\)
0.502654
\(q = \frac{{4\pi }}{{25}},{\text{ }}0.503{\text{ }}\left( {{\text{or }} – \frac{{4\pi }}{{25}},{\text{ }} – 0.503} \right)\) A1 N2
[3 marks]
valid method to find \(r\) (M1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{max}} + {\text{min}}}}{2},{\text{ }}0.6 + 0.45\)
\(r = 1.05\) A1 N2
[2 marks]
METHOD 1
attempt to find start or end \(t\)-values for 12 December (M1)
eg\(\,\,\,\,\,\)\(3 + 24,{\text{ }}t = 27,{\text{ }}t = 51\)
finds \(t\)-value for second max (A1)
\(t = 50\)
23:00 (or 11 pm) A1 N3
METHOD 2
valid approach to list either the times of high tides after 21:00 or the \(t\)-values of high tides after 21:00, showing at least two times (M1)
eg\(\,\,\,\,\,\)\({\text{21:00}} + 12.5,{\text{ 21:00}} + 25,{\text{ }}12.5 + 12.5,{\text{ }}25 + 12.5\)
correct time of first high tide on 12 December (A1)
eg\(\,\,\,\,\,\)10:30 (or 10:30 am)
time of second high tide = 23:00 A1 N3
METHOD 3
attempt to set their \(h\) equal to 1.5 (M1)
eg\(\,\,\,\,\,\)\(h(t) = 1.5,{\text{ }}0.45\cos \left( {\frac{{4\pi }}{{25}}t} \right) + 1.05 = 1.5\)
correct working to find second max (A1)
eg\(\,\,\,\,\,\)\(0.503t = 8\pi ,{\text{ }}t = 50\)
23:00 (or 11 pm) A1 N3
[3 marks]
Question
The diagram shows a circle, centre O, with radius 4 cm. Points A and B lie on the circumference of the circle and AÔB = θ , where 0 ≤ θ ≤ \(\pi \).
Find the area of the shaded region, in terms of θ.
The area of the shaded region is 12 cm2. Find the value of θ.
Answer/Explanation
Markscheme
valid approach to find area of segment (M1)
eg area of sector – area of triangle, \(\frac{1}{2}{r^2}\left( {\theta – {\text{sin}}\theta } \right)\)
correct substitution (A1)
eg \(\frac{1}{4}{\left( 4 \right)^2}\theta – \frac{1}{2}{\left( 4 \right)^2}{\text{sin}}\theta ,\,\,\frac{1}{2} \times 16\left[ {\theta – {\text{sin}}\theta } \right]\)
area = 80 – 8 sinθ, 8(θ – sinθ) A1 N2
[3 marks]
setting their area expression equal to 12 (M1)
eg 12 = 8(θ – sinθ)
2.26717
θ = 2.27 (do not accept an answer in degrees) A2 N3
[3 marks]
Question
At an amusement park, a Ferris wheel with diameter 111 metres rotates at a constant speed. The bottom of the wheel is k metres above the ground. A seat starts at the bottom of the wheel.
The wheel completes one revolution in 16 minutes.
After t minutes, the height of the seat above ground is given by \(h\left( t \right) = 61.5 + a\,{\text{cos}}\left( {\frac{\pi }{8}t} \right)\), for 0 ≤ t ≤ 32.
After 8 minutes, the seat is 117 m above the ground. Find k.
Find the value of a.
Find when the seat is 30 m above the ground for the third time.
Answer/Explanation
Markscheme
valid approach to find k (M1)
eg 8 minutes is half a turn, k + diameter, k + 111 = 117
k = 6 A1 N2
[2 marks]
METHOD 1
valid approach (M1)
eg \(\frac{{{\text{max}}\,\, – \,\,{\text{min}}}}{2}\) a = radius
\(\left| a \right| = \frac{{117 – 6}}{2},\,\,55.5\) (A1)
a = −55.5 A1 N2
METHOD 2
attempt to substitute valid point into equation for f (M1)
eg h(0) = 6, h(8) = 117
correct equation (A1)
eg \(6 = 61.5 + a\,{\text{cos}}\left( {\frac{\pi }{8} \times 0} \right),\,\,117 = 61.5 + a\,{\text{cos}}\left( {\frac{\pi }{8} \times 8} \right),\,\,6 = 61.5 + a\)
a = −55.5 A1 N2
[3 marks]
valid approach (M1)
eg sketch of h and \(y = 30,\,\,h = 30,\,\,61.5 – 55.5\,{\text{cos}}\left( {\frac{\pi }{8}t} \right) = 30,\,\,t = 2.46307,\,\,t = 13.5369\)
18.4630
t = 18.5 (minutes) A1 N3
[3 marks]
Question
A circle centre O and radius \(r\) is shown below. The chord [AB] divides the area of the circle into two parts. Angle AOB is \(\theta \) .
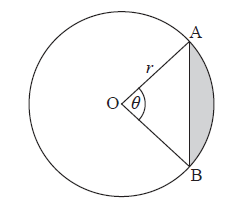
Find an expression for the area of the shaded region.
The chord [AB] divides the area of the circle in the ratio 1:7. Find the value of \(\theta \) .
Answer/Explanation
Markscheme
substitution into formula for area of triangle A1
e.g. \(\frac{1}{2}r \times r\sin \theta \)
evidence of subtraction M1
correct expression A1 N2
e.g. \(\frac{1}{2}{r^2}\theta – \frac{1}{2}{r^2}\sin \theta \) , \(\frac{1}{2}{r^2}(\theta – \sin \theta )\)
[3 marks]
evidence of recognizing that shaded area is \(\frac{1}{8}\) of area of circle M1
e.g. \(\frac{1}{8}\) seen anywhere
setting up correct equation A1
e.g. \(\frac{1}{2}{r^2}(\theta – \sin \theta ) = \frac{1}{8}\pi {r^2}\)
eliminating 1 variable M1
e.g. \(\frac{1}{2}(\theta – \sin \theta ) = \frac{1}{8}\pi \) , \(\theta – \sin \theta = \frac{\pi }{4}\)
attempt to solve M1
e.g. a sketch, writing \(\sin x – x + \frac{\pi }{4} = 0\)
\(\theta = 1.77\) (do not accept degrees) A1 N1
[5 marks]