Download IITian Academy App for accessing Online Mock Tests and More..
Question
A ship leaves port A on a bearing of \(030^\circ \) . It sails a distance of \(25{\text{ km}}\) to point B. At B, the ship changes direction to a bearing of \(100^\circ \) . It sails a distance of \(40{\text{ km}}\) to reach point C. This information is shown in the diagram below.
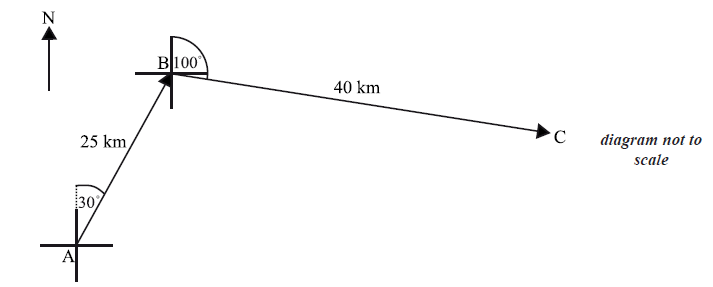
A second ship leaves port A and sails directly to C.
Find the distance the second ship will travel.
Find the bearing of the course taken by the second ship.
Answer/Explanation
Markscheme
finding \({\text{A}}\widehat {\rm{B}}{\rm{C}} = 110^\circ \) (\( = 1.92\) radians) (A1)
evidence of choosing cosine rule (M1)
e.g. \({\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^2} – 2({\rm{AB}})({\rm{BC}})\cos {\rm{A}}\widehat {\rm{B}}{\rm{C}}\)
correct substitution A1
e.g. \({\rm{A}}{{\rm{C}}^2} = {25^2} + {40^2} – 2(25)(40)\cos 110^\circ \)
\({\rm{A}}{{\rm{C}}^{}} = 53.9\) (km) A1
METHOD 1
correct substitution into the sine rule A1
e.g. \(\frac{{\sin {\rm{B}}\widehat {\rm{A}}{\rm{C}}}}{{40}} = \frac{{\sin 110^\circ }}{{53.9}}\) A1
\({\rm{B}}\widehat {\rm{A}}{\rm{C}} = 44.2^\circ \)
bearing \( = 074^\circ \) A1 N1
METHOD 2
correct substitution into the cosine rule A1
e.g. \(\cos {\rm{B}}\widehat {\rm{A}}{\rm{C}} = \frac{{{{40}^2} – {{25}^2} – {{53.9}^2}}}{{ – 2(25)(53.9)}}\) A1
\({\rm{B}}\widehat {\rm{A}}{\rm{C}} = 44.3^\circ \)
bearing \( = 074^\circ \) A1 N1
[3 marks]
Question
The circle shown has centre O and radius 3.9 cm.
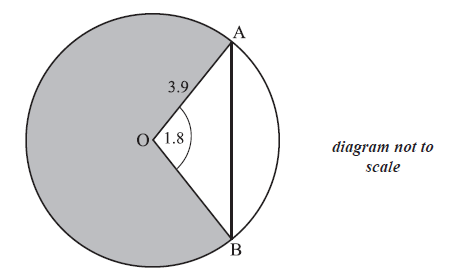
Points A and B lie on the circle and angle AOB is 1.8 radians.
Find AB.
Find the area of the shaded region.
Answer/Explanation
Markscheme
METHOD 1
choosing cosine rule (M1)
substituting correctly A1
e.g. \({\rm{AB}} = \sqrt {{{3.9}^2} + {{3.9}^2} – 2(3.9)(3.9)\cos 1.8} \)
\({\rm{AB}} = 6.11\) (cm) A1 N2
METHOD 2
evidence of approach involving right-angled triangles (M1)
substituting correctly A1
e.g. \(\sin 0.9 = \frac{x}{{3.9}}\) , \(\frac{1}{2}{\rm{AB}} = 3.9\sin 0.9\)
\({\rm{AB}} = 6.11\) (cm) A1 N2
METHOD 3
choosing the sine rule (M1)
substituting correctly A1
e.g. \(\frac{{\sin 0.670 \ldots }}{{3.9}} = \frac{{\sin 1.8}}{{{\rm{AB}}}}\)
\({\rm{AB}} = 6.11\) (cm) A1 N2
[3 marks]
METHOD 1
reflex \({\rm{A}}\widehat {\rm{O}}{\rm{B}} = 2\pi – 1.8\) \(( = 4.4832)\) (A2)
correct substitution \(A = \frac{1}{2}{(3.9)^2}(4.4832 \ldots )\) A1
area =34.1 (cm2) A1 N2
METHOD 2
finding area of circle \(A = \pi {(3.9)^2}\) \(( = 47.78 \ldots )\) (A1)
finding area of (minor) sector \(A = \frac{1}{2}{(3.9)^2}(1.8)\) \(( = 13.68 \ldots )\) (A1)
subtracting M1
e.g. \(\pi {(3.9)^2} – 0.5{(3.9)^2}(1.8)\) , \(47.8 – 13.7\)
area = 34.1 (cm2) A1 N2
METHOD 3
finding reflex \({\rm{A}}\widehat {\rm{O}}{\rm{B}} = 2\pi – 1.8\) \(( = 4.4832)\) (A2)
finding proportion of total area of circle A1
e.g. \(\frac{{2\pi – 1.8}}{{2\pi }} \times \pi {(3.9)^2}\) , \(\frac{\theta }{{2\pi }} \times \pi {r^2}\)
area = 34.1 (cm2) A1 N2
[4 marks]
Question
The diagram below shows a triangle ABD with AB =13 cm and AD = 6.5 cm.
Let C be a point on the line BD such that BC = AC = 7 cm.
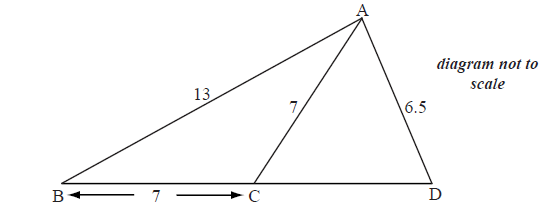
Find the size of angle ACB.
Find the size of angle CAD.
Answer/Explanation
Markscheme
METHOD 1
evidence of choosing the cosine formula (M1)
correct substitution A1
e.g. \(\cos {\rm{A}}\widehat {\rm{C}}{\rm{B}} = \frac{{{7^2} + {7^2} – {{13}^2}}}{{2 \times 7 \times 7}}\)
\({\rm{A}}\widehat {\rm{C}}{\rm{B}} = 2.38\) radians \(( = 136^\circ )\) A1 N2
METHOD 2
evidence of appropriate approach involving right-angled triangles (M1)
correct substitution A1
e.g. \(\sin \left( {\frac{1}{2}{\rm{A}}\widehat {\rm{C}}{\rm{B}}} \right) = \frac{{6.5}}{7}\)
\({\rm{A}}\widehat {\rm{C}}{\rm{B}} = 2.38\) radians \(( = 136^\circ )\) A1 N2
[3 marks]
METHOD 1
\({\rm{A}}\widehat {\rm{C}} {\rm{D}} = \pi – 2.381\) \((180 – 136.4)\) (A1)
evidence of choosing the sine rule in triangle ACD (M1)
correct substitution A1
e.g. \(\frac{{6.5}}{{\sin 0.760 \ldots }} = \frac{7}{{\sin {\rm{A}}\widehat {\rm{D}} {\rm{C}}}}\)
\({\rm{A}}\widehat {\rm{D}}{\rm{C}} = 0.836 \ldots \) \(( = 47.9 \ldots ^\circ )\) A1
\({\rm{C}}\widehat {\rm{A}}{\rm{D}} = \pi – (0.760 \ldots + 0.836 \ldots )\) \((180 – (43.5 \ldots + 47.9 \ldots ))\)
\( = 1.54\) \(( = 88.5^\circ )\) A1 N3
METHOD 2
\({\rm{A}}\widehat {\rm{B}}{\rm{C}} = \frac{1}{2}(\pi – 2.381)\) \(\left( {\frac{1}{2}(180 – 136.4)} \right)\) (A1)
evidence of choosing the sine rule in triangle ABD (M1)
correct substitution A1
e.g. \(\frac{{6.5}}{{\sin 0.380 \ldots }} = \frac{{13}}{{\sin {\rm{A}}\widehat {\rm{D}}{\rm{C}}}}\)
\({\rm{A}}\widehat {\rm{D}}{\rm{C}} = 0.836 \ldots \) \(( = 47.9 \ldots ^\circ )\) A1
\({\rm{C}}\widehat {\rm{A}}{\rm{D}} = \pi – 0.836 \ldots – (\pi – 2.381 \ldots )\) \(( = 180 – 47.9 \ldots – (180 – 136.4))\)
\( = 1.54\) \(( = 88.5^\circ )\) A1 N3
Note: Two triangles are possible with the given information. If candidate finds \({\rm{A}}\widehat {\rm{D}}{\rm{C}} = 2.31\) \((132^\circ )\) leading to \({\rm{C}}\widehat {\rm{A}}{\rm{D}} = 0.076\) \((4.35^\circ )\) , award marks as per markscheme.
[5 marks]
Question
The following diagram shows a circle with centre O and radius 4 cm.
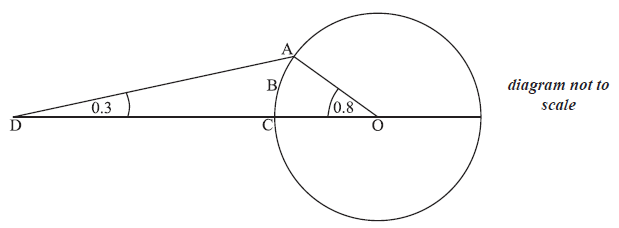
The points A, B and C lie on the circle. The point D is outside the circle, on (OC).
Angle ADC = 0.3 radians and angle AOC = 0.8 radians.
Find AD.
Find OD.
Find the area of sector OABC.
Find the area of region ABCD.
Answer/Explanation
Markscheme
choosing sine rule (M1)
correct substitution A1
e.g. \(\frac{{{\rm{AD}}}}{{\sin 0.8}} = \frac{4}{{\sin 0.3}}\)
\({\text{AD}} = 9.71{\text{ (cm)}}\) A1 N2
[3 marks]
METHOD 1
finding angle \({\rm{OAD}} = \pi – 1.1 = (2.04)\) (seen anywhere) (A1)
choosing cosine rule (M1)
correct substitution A1
e.g. \({\rm{O}}{{\rm{D}}^2} = {9.71^2} + {4^2} – 2 \times 9.71 \times 4 \times \cos (\pi – 1.1)\)
\({\text{OD}} = 12.1{\text{ (cm)}}\) A1 N3
METHOD 2
finding angle \({\rm{OAD}} = \pi – 1.1 = (2.04)\) (seen anywhere) (A1)
choosing sine rule (M1)
correct substitution A1
e.g. \(\frac{{{\rm{OD}}}}{{\sin (\pi – 1.1)}} = \frac{{9.71}}{{\sin 0.8}} = \frac{4}{{\sin 0.3}}\)
\({\text{OD}} = 12.1{\text{ (cm)}}\) A1 N3
[4 marks]
correct substitution into area of a sector formula (A1)
e.g. \({\rm{area}} = 0.5 \times {4^2} \times 0.8\)
\({\text{area}} = 6.4{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1 N2
[2 marks]
substitution into area of triangle formula OAD (M1)
correct substitution A1
e.g. \(A{\rm{ = }}\frac{1}{2} \times 4 \times 12.1 \times \sin 0.8\) , \(A{\rm{ = }}\frac{1}{2} \times 4 \times 9.71 \times \sin 2.04\) , \(A{\rm{ = }}\frac{1}{2} \times 12.1 \times 9.71 \times \sin 0.3\)
subtracting area of sector OABC from area of triangle OAD (M1)
e.g. \({\text{area ABCD}} = 17.3067 – 6.4\)
\({\text{area ABCD}} = 10.9{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1 N2
[4 marks]
Question
The diagram below shows a quadrilateral ABCD with obtuse angles \({\rm{A}}\widehat {\rm{B}}{\rm{C}}\) and \({\rm{A}}\widehat {\rm{D}}{\rm{C}}\).
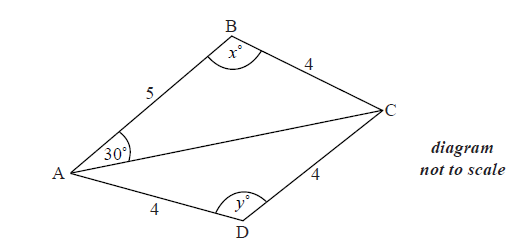
AB = 5 cm, BC = 4 cm, CD = 4 cm, AD = 4 cm , \({\rm{B}}\widehat {\rm{A}}{\rm{C}} = {30^ \circ }\) , \({\rm{A}}\widehat {\rm{B}}{\rm{C}} = {x^ \circ }\) , \({\rm{A}}\widehat {\rm{D}}{\rm{C}} = {y^ \circ }\) .
Use the cosine rule to show that \({\rm{AC}} = \sqrt {41 – 40\cos x} \) .
Use the sine rule in triangle ABC to find another expression for AC.
(i) Hence, find x, giving your answer to two decimal places.
(ii) Find AC .
(i) Find y.
(ii) Hence, or otherwise, find the area of triangle ACD.
Answer/Explanation
Markscheme
correct substitution A1
e.g. \(25 + 16 – 40\cos x\) , \({5^2} + {4^2} – 2 \times 4 \times 5\cos x\)
\({\rm{AC}} = \sqrt {41 – 40\cos x} \) AG
[1 mark]
correct substitution A1
e.g. \(\frac{{{\rm{AC}}}}{{\sin x}} = \frac{4}{{\sin 30}}\) , \(\frac{1}{2}{\rm{AC}} = 4\sin x\)
\({\rm{AC}} = 8\sin x\) (accept \(\frac{{4\sin x}}{{\sin 30}}\)) A1 N1
[2 marks]
(i) evidence of appropriate approach using AC M1
e.g. \(8\sin x = \sqrt {41 – 40\cos x} \) , sketch showing intersection
correct solution \(8.682 \ldots \), \(111.317 \ldots \) (A1)
obtuse value \(111.317 \ldots \) (A1)
\(x = 111.32\) to 2 dp (do not accept the radian answer 1.94 ) A1 N2
(ii) substituting value of x into either expression for AC (M1)
e.g. \({\rm{AC}} = 8\sin 111.32\)
\({\rm{AC}} = 7.45\) A1 N2
[6 marks]
(i) evidence of choosing cosine rule (M1)
e.g. \(\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}}\)
correct substitution A1
e.g. \(\frac{{{4^2} + {4^2} – {{7.45}^2}}}{{2 \times 4 \times 4}}\) , \({7.45^2} = 32 – 32\cos y\) , \(\cos y = – 0.734 \ldots \)
\(y = 137\) A1 N2
(ii) correct substitution into area formula (A1)
e.g. \(\frac{1}{2} \times 4 \times 4 \times \sin 137\) , \(8\sin 137\)
area \(= 5.42\) A1 N2
[5 marks]
The diagram below shows a circle with centre O and radius 8 cm.
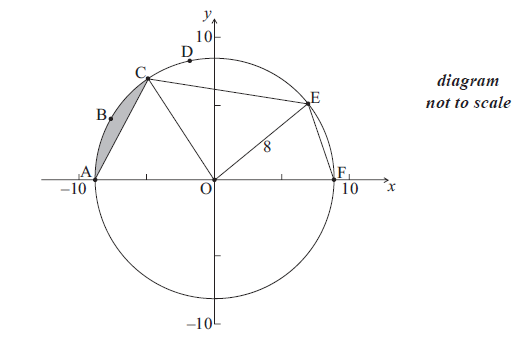
The points A, B, C, D, E and F are on the circle, and [AF] is a diameter. The length of arc ABC is 6 cm.
Find the size of angle AOC .
Hence find the area of the shaded region.
The area of sector OCDE is \(45{\text{ c}}{{\text{m}}^2}\).
Find the size of angle COE .
Find EF .
Answer/Explanation
Markscheme
appropriate approach (M1)
e.g. \(6 = 8\theta \)
\({\rm{A}}\widehat {\rm{O}}{\rm{C}} = 0.75\) A1 N2
[2 marks]
evidence of substitution into formula for area of triangle (M1)
e.g. \({\rm{area}} = \frac{1}{2} \times 8 \times 8 \times \sin (0.75)\)
area \(= 21.8 \ldots \) (A1)
evidence of substitution into formula for area of sector (M1)
e.g. \({\rm{area}} = \frac{1}{2} \times 64 \times 0.75\)
area of sector \(= 24\) (A1)
evidence of substituting areas (M1)
e.g. \(\frac{1}{2}{r^2}\theta – \frac{1}{2}ab\sin C\) , \({\text{area of sector}} – {\text{area of triangle}}\)
area of shaded region \( = 2.19{\text{ c}}{{\text{m}}^2}\) A1 N4
[6 marks]
attempt to set up an equation for area of sector (M1)
e.g. \(45 = \frac{1}{2} \times {8^2} \times \theta \)
\({\rm{C}}\widehat {\rm{O}}{\rm{E}} = 1.40625\) (1.41 to 3 sf) A1 N2
[2 marks]
METHOD 1
attempting to find angle EOF (M1)
e.g. \(\pi – 0.75 – 1.41\)
\({\rm{E}}\widehat {\rm{O}}{\rm{F}} = 0.985\) (seen anywhere) A1
evidence of choosing cosine rule (M1)
correct substitution A1
e.g. \({\rm{EF}} = \sqrt {{8^2} + {8^2} – 2 \times 8 \times 8 \times \cos 0.985} \)
EF \(= 7.57{\text{ cm}}\) A1 N3
METHOD 2
attempting to find angles that are needed (M1)
e.g. angle EOF and angle OEF
\({\rm{E}}\widehat {\rm{O}}{\rm{F}} = 0.9853 \ldots \) and \({\text{O}}\widehat {\rm{E}}{\text{F (or O}}\widehat {\text{F}}{\text{E)}} = 1.078 \ldots \) A1
evidence of choosing sine rule (M1)
correct substitution (A1)
e.g. \(\frac{{{\rm{EF}}}}{{\sin 0.985}} = \frac{8}{{\sin 1.08}}\)
EF \(= 7.57{\text{ cm}}\) A1 N3
METHOD 3
attempting to find angle EOF (M1)
e.g. \(\pi – 0.75 – 1.41\)
\({\rm{E}}\widehat {\rm{O}}{\rm{F}} = 0.985\) (seen anywhere) A1
evidence of using half of triangle EOF (M1)
e.g. \(x = 8\sin \frac{{0.985}}{2}\)
correct calculation A1
e.g. \(x = 3.78\)
EF \(= 7.57{\text{ cm}}\) A1 N3
[5 marks]
Question
The following diagram shows the triangle ABC.
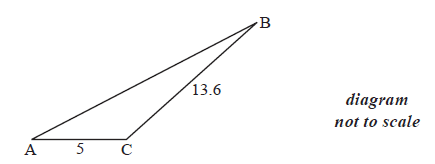
The angle at C is obtuse, \({\text{AC}} = 5{\text{ cm}}\), \({\text{BC}} =13.6{\text{ cm}}\) and the area is \(20{\text{ c}}{\text{m}}^2\) .
Find \({\rm{A}}\widehat {\rm{C}}{\rm{B}}\) .
Find AB.
Answer/Explanation
Markscheme
correct substitution into the formula for the area of a triangle A1
e.g. \(\frac{1}{2} \times 5 \times 13.6 \times \sin C = 20\) , \(\frac{1}{2} \times 5 \times h = 20\)
attempt to solve (M1)
e.g. \(\sin C = 0.5882 \ldots \) , \(\sin C = \frac{8}{{13.6}}\)
\(\widehat C = 36.031 \ldots ^\circ \) (\(0.6288 \ldots {\text{ radians}}\)) (A1)
\({\rm{A}}\widehat {\rm{C}}{\rm{B}} = 144^\circ \) \((2.51{\text{ radians}})\) A1 N3
[4 marks]
evidence of choosing the cosine rule (M1)
correct substitution A1
e.g. \({({\rm{AB}})^2} = {5^2} + {13.6^2} – 2(5)(13.6)\cos 143.968 \ldots \)
\({\text{AB}} = 17.9\) A1 N2
[3 marks]
Question
The following diagram shows triangle ABC .
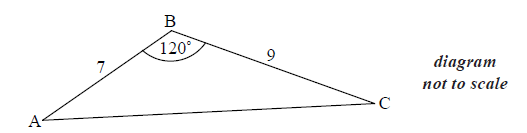
AB = 7 cm, BC = 9 cm and \({\rm{A}}\widehat {\rm{B}}{\rm{C}} = {120^ \circ }\) .
Find AC .
Find \({\rm{B}}\widehat {\rm{A}}{\rm{C}}\) .
Answer/Explanation
Markscheme
evidence of choosing cosine rule (M1)
e.g. \({a^2} + {b^2} – 2ab\cos C\)
correct substitution A1
e.g. \({7^2} + {9^2} – 2(7)(9)\cos {120^ \circ }\)
\({\text{AC}} = 13.9\) \(\left( { = \sqrt {193} } \right)\) A1 N2
[3 marks]
METHOD 1
evidence of choosing sine rule (M1)
e.g. \(\frac{{\sin \widehat A}}{{{\rm{BC}}}} = \frac{{\sin \widehat B}}{{{\rm{AC}}}}\)
correct substitution A1
e.g. \(\frac{{\sin \widehat A}}{9} = \frac{{\sin 120}}{{13.9}}\)
\(\widehat A = {34.1^ \circ }\) A1 N2
METHOD 2
evidence of choosing cosine rule (M1)
e.g. \(\cos \widehat A = \frac{{{\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2} – {\rm{B}}{{\rm{C}}^2}}}{{2({\rm{AB}})({\rm{AC}})}}\)
correct substitution A1
e.g. \(\cos \widehat A = \frac{{{7^2} + {{13.9}^2} – {9^2}}}{{2(7)(13.9)}}\)
\(\widehat A = {34.1^ \circ }\) A1 N2
[3 marks]
Question
There is a vertical tower TA of height 36 m at the base A of a hill. A straight path goes up the hill from A to a point U. This information is represented by the following diagram.
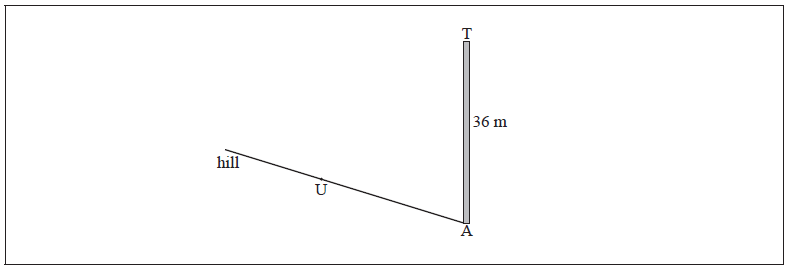
The path makes a \({4^ \circ }\) angle with the horizontal.
The point U on the path is \(25{\text{ m}}\) away from the base of the tower.
The top of the tower is fixed to U by a wire of length \(x{\text{ m}}\).
Complete the diagram, showing clearly all the information above.
Find x .
Answer/Explanation
Markscheme
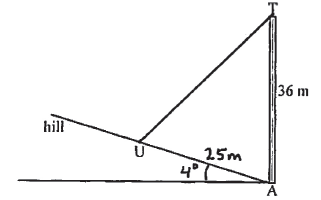A1A1A1 N3
Note: Award A1 for labelling \({4^ \circ }\) with horizontal, A1 for labelling [AU] 25 metres, A1 for drawing [TU].
[3 marks]
\({\rm{T}}\widehat {\rm{A}}{\rm{U}} = {86^ \circ }\) (A1)
evidence of choosing cosine rule (M1)
correct substitution A1
e.g. \({x^2} = {25^2} + {36^2} – 2(25)(36)\cos {86^ \circ }\)
\(x = 42.4\) A1 N3
[4 marks]
Question
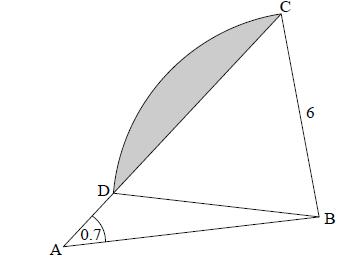
The following diagram shows a triangle ABC.
\({\rm{BC}} = 6\) , \({\rm{C}}\widehat {\rm{A}}{\rm{B}} = 0.7\) radians , \({\rm{AB}} = 4p\) , \({\rm{AC}} = 5p\) , where \(p > 0\) .
Consider the circle with centre B that passes through the point C. The circle cuts the line CA at D, and \({\rm{A}}\widehat {\rm{D}}{\rm{B}}\) is obtuse. Part of the circle is shown in the following diagram.
(i) Show that \({p^2}(41 – 40\cos 0.7) = 36\) .
(ii) Find p .
Write down the length of BD.
Find \({\rm{A}}\widehat {\rm{D}}{\rm{B}}\) .
(i) Show that \({\rm{C}}\widehat {\rm{B}}{\rm{D}} = 1.29\) radians, correct to 2 decimal places.
(ii) Hence, find the area of the shaded region.
Answer/Explanation
Markscheme
(i) evidence of valid approach (M1)
e.g. choosing cosine rule
correct substitution (A1)
e.g. \({6^2} = {(5p)^2} + {(4p)^2} – 2 \times (4p) \times (5p)\cos 0.7\)
simplification A1
e.g. \(36 = 25{p^2} + 16{p^2} – 40{p^2}\cos 0.7\)
\({p^2}(41 – 40\cos 0.7) = 36\) AG N0
(ii) \(1.85995 \ldots \)
\(p = 1.86\) A1 N1
Note: Award A0 for \(p = \pm 1.86\) , i.e. not rejecting the negative value.
[4 marks]
\({\text{BD}} = 6\) A1 N1
[1 mark]
evidence of valid approach (M1)
e.g. choosing sine rule
correct substitution A1
e.g. \(\frac{{\sin {\rm{A}}\widehat {\rm{D}}{\rm{B}}}}{{4p}} = \frac{{\sin 0.7}}{6}\)
\({\text{acute }}{\rm{A}}\widehat {\rm{D}}{\rm{B = 0}}{\rm{.9253166}} \ldots \) (A1)
\(\pi – 0.9253166 \ldots = 2.216275 \ldots \)
\({\rm{A}}\widehat {\rm{D}}{\rm{B}} = 2.22\) A1 N3
[4 marks]
(i) evidence of valid approach (M1)
e.g. recognize isosceles triangle, base angles equal
\(\pi – 2(0.9253 \ldots )\) A1
\({\rm{C}}\widehat {\rm{B}}{\rm{D}} = 1.29\) AG N0
(ii) area of sector BCD (A1)
e.g. \(0.5 \times (1.29) \times {(6)^2}\)
area of triangle BCD (A1)
e.g. \(0.5 \times {(6)^2}\sin 1.29\)
evidence of subtraction M1
\(5.92496 \ldots \)
\(5.937459 \ldots \)
\({\text{area}} = 5.94\) A1 N3
[6 marks]
Question
Consider the following circle with centre O and radius r .
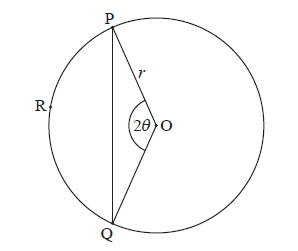
The points P, R and Q are on the circumference, \({\rm{P}}\widehat {\rm{O}}{\rm{Q}} = 2\theta \) , for \(0 < \theta < \frac{\pi }{2}\) .
Use the cosine rule to show that \({\rm{PQ}} = 2r\sin \theta \) .
Let l be the length of the arc PRQ .
Given that \(1.3{\rm{PQ}} – l = 0\) , find the value of \(\theta \) .
Consider the function \(f(\theta ) = 2.6\sin \theta – 2\theta \) , for \(0 < \theta < \frac{\pi }{2}\) .
(i) Sketch the graph of f .
(ii) Write down the root of \(f(\theta ) = 0\) .
Use the graph of f to find the values of \(\theta \) for which \(l < 1.3{\rm{PQ}}\) .
Answer/Explanation
Markscheme
correct substitution into cosine rule A1
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = {r^2} + {r^2} – 2(r)(r)\cos (2\theta )\) , \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2}(\cos (2\theta ))\)
substituting \(1 – 2{\sin ^2}\theta \) for \(\cos 2\theta \) (seen anywhere) A1
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2}(1 – 2{\sin ^2}\theta )\)
working towards answer (A1)
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 2{r^2} – 2{r^2} + 4{r^2}{\sin ^2}\theta \)
recognizing \(2{r^2} – 2{r^2} = 0\) (including crossing out) (seen anywhere)
e.g. \({\rm{P}}{{\rm{Q}}^{\rm{2}}} = 4{r^2}{\sin ^2}\theta \) , \({\rm{PQ}} = \sqrt {4{r^2}{{\sin }^2}\theta } \)
\({\rm{PQ = 2}}r{\rm{sin}}\theta \) AG N0
[4 marks]
\({\rm{PRQ}} = r \times 2\theta \) (seen anywhere) (A1)
correct set up A1
e.g. \(1.3 \times 2r\sin \theta – r \times (2\theta ) = 0\)
attempt to eliminate r (M1)
correct equation in terms of the one variable \(\theta \) (A1)
e.g. \(1.3 \times 2\sin \theta – 2\theta = 0\)
1.221496215
\(\theta = 1.22\) (accept \(70.0^\circ \) (69.9)) A1 N3
[5 marks]
(i)
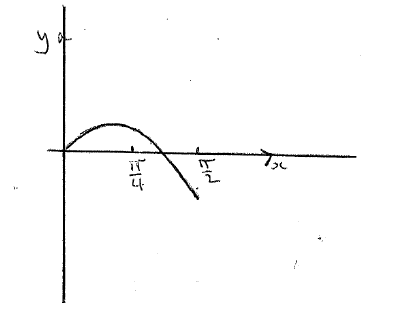
A1A1A1 N3
Note: Award A1 for approximately correct shape, A1 for x-intercept in approximately correct position, A1 for domain. Do not penalise if sketch starts at origin.
(ii) \(1.221496215\)
\(\theta = 1.22\) A1 N1
[4 marks]
evidence of appropriate approach (may be seen earlier) M2
e.g. \(2\theta < 2.6\sin \theta \) , \(0 < f(\theta )\) , showing positive part of sketch
\(0 < \theta < 1.221496215\)
\(0 < \theta = 1.22\) (accept \(\theta < 1.22\) ) A1 N1
[3 marks]
Examiners report
This exercise seemed to be challenging for the great majority of the candidates, in particular parts (b), (c) and (d).
Part (a) was generally attempted using the cosine rule, but many failed to substitute correctly into the right hand side or skipped important steps. A high percentage could not arrive at the given expression due to a lack of knowledge of trigonometric identities or making algebraic errors, and tried to force their way to the given answer.
The most common errors included taking the square root too soon, and sign errors when distributing the negative after substituting \(\cos 2\theta \) by \(1 – 2{\sin ^2}\theta \) .
This exercise seemed to be challenging for the great majority of the candidates, in particular parts (b), (c) and (d).
In part (b), most candidates understood what was required but could not find the correct length of the arc PRQ mainly due to substituting the angle by \(\theta \) instead of \(2\theta \) .
Regarding part (c), many valid approaches were seen for the graph of f, making a good use of their GDC. A common error was finding a second or third solution outside the domain. A considerable amount of sketches were missing a scale.
There were candidates who achieved the correct equation but failed to realize they could use their GDC to solve it.
Part (d) was attempted by very few, and of those who achieved the correct answer not many were able to show the method they used.
Question
The following diagram shows a circular play area for children.
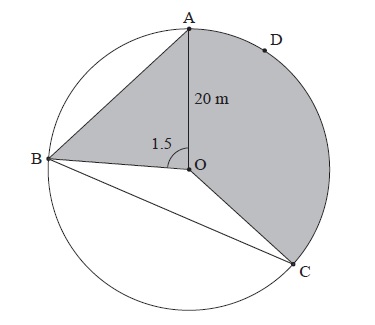
The circle has centre O and a radius of 20 m, and the points A, B, C and D lie on the circle. Angle AOB is 1.5 radians.
Find the length of the chord [AB].
Find the area of triangle AOB.
Angle BOC is 2.4 radians.
Find the length of arc ADC.
Angle BOC is 2.4 radians.
Find the area of the shaded region.
Angle BOC is 2.4 radians.
The shaded region is to be painted red. Red paint is sold in cans which cost \(\$ 32\) each. One can covers \(140{\text{ }}{{\text{m}}^2}\). How much does it cost to buy the paint?
Answer/Explanation
Markscheme
Note: In this question, do not penalise for missing or incorrect units. They are not included in the markscheme, to avoid complex answer lines.
METHOD 1
choosing cosine rule (must have cos in it) (M1)
e.g. \({c^2} = {a^2} + {b^2} – 2ab\cos C\)
correct substitution (into rhs) A1
e.g. \({20^2} + {20^2} – 2(20)(20)\cos 1.5\) , \({\rm{AB}} = \sqrt {800 – 800\cos 1.5} \)
\({\rm{AB = 27}}{\rm{.26555}} \ldots \)
\({\rm{AB}} = 27.3\) \([27.2{\text{, }}27.3]\) A1 N2
[3 marks]
METHOD 2
choosing sine rule (M1)
e.g. \(\frac{{\sin A}}{a} = \frac{{\sin B}}{b}\) , \(\frac{{{\rm{AB}}}}{{\sin O}} = \frac{{{\rm{AO}}}}{{\sin B}}\)
correct substitution A1
e.g. \(\frac{{{\rm{AB}}}}{{\sin 1.5}} = \frac{{20}}{{\sin (0.5(\pi – 1.5))}}\)
\({\rm{AB}} = 27.26555 \ldots \)
\({\rm{AB}} = 27.3\) \([27.2{\text{, }}27.3]\) A1 N2
[3 marks]
correct substitution into area formula A1
e.g. \(\frac{1}{2}(20)(20)\sin 1.5\) , \(\frac{1}{2}(20)(27.2655504 \ldots )\sin(0.5(\pi – 1.5))\)
\({\rm{area}} = 199.498997 \ldots \) (accept \(199.75106 = 200\) , from using 27.3)
\({\rm{area}} = 199\) \([199{\text{, }}200]\) A1 N1
[2 marks]
appropriate method to find angle AOC (M1)
e.g. \(2\pi – 1.5 – 2.4\)
correct substitution into arc length formula (A1)
e.g. \((2\pi – 3.9) \times 20\) , \(2.3831853 \ldots \times 20\)
\({\text{arc length}} = 47.6637 \ldots \)
\({\text{arc length}} = 47.7\) \((47.6{\text{, }}47.7]\) (i.e. do not accept \(47.6\)) A1 N2
Notes: Candidates may misread the question and use \({\rm{A}}\widehat {\rm{O}}{\rm{C}} = 2.4\) . If working shown, award M0 then A0MRA1 for the answer 48. Do not then penalize \({\rm{A}}\widehat {\rm{O}}{\rm{C}}\) in part (d) which, if used, leads to the answer \(679.498 \ldots \)
However, if they use the prematurely rounded value of 2.4 for \({\rm{A}}\widehat {\rm{O}}{\rm{C}}\) , penalise 1 mark for premature rounding for the answer 48 in (c). Do not then penalize for this in (d).
[3 marks]
calculating sector area using their angle AOC (A1)
e.g. \(\frac{1}{2}(2.38 \ldots )({20^2})\) , \(200(2.38 \ldots )\) , \(476.6370614 \ldots \)
shaded area = their area of triangle AOB + their area of sector (M1)
e.g. \(199.4989973 \ldots + 476.6370614 \ldots \) , \(199 + 476.637\)
\({\text{shaded area}} = 676.136 \ldots \) (accept \(675.637 \ldots = 676\) from using 199)
\({\text{shaded area}} = 676\) \([676{\text{, }}677]\) A1 N2
[3 marks]
dividing to find number of cans (M1)
e.g. \(\frac{{676}}{{140}}\) , \(4.82857 \ldots \)
5 cans must be purchased (A1)
multiplying to find cost of cans (M1)
e.g. \(5(32)\) , \(\frac{{676}}{{140}} \times 32\)
cost is 160 (dollars) A1 N3
[4 marks]
Question
The diagram shows a circle of radius \(8\) metres. The points ABCD lie on the circumference of the circle.
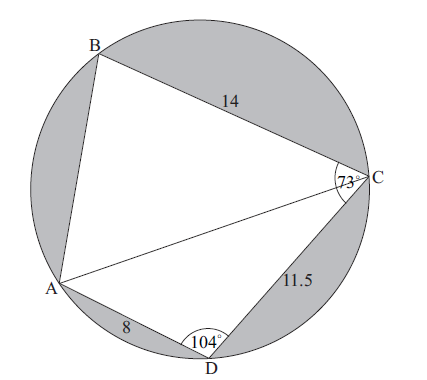
BC = \(14\) m, CD = \(11.5\) m, AD = \(8\) m, \(A\hat DC = {104^ \circ }\) , and \(B\hat CD = {73^ \circ }\) .
Find AC.
(i) Find \(A\hat CD\) .
(ii) Hence, find \(A\hat CB\) .
Find the area of triangle ADC.
(c) Find the area of triangle ADC.
(d) Hence or otherwise, find the total area of the shaded regions.
Hence or otherwise, find the total area of the shaded regions.
Answer/Explanation
Markscheme
evidence of choosing cosine rule (M1)
eg \({c^2} = {a^2} + {b^2} – 2ab\cos C\) , \({\rm{C}}{{\rm{D}}^2} + {\rm{A}}{{\rm{D}}^2} – 2 \times {\rm{CD}} \times {\rm{AD}}\cos D\)
correct substitution A1
eg \({11.5^2} + {8^2} – 2 \times 11.5 \times 8\cos 104\) , \(196.25 – 184\cos 104\)
AC \( = 15.5\) (m) A1 N2
[3 marks]
(i) METHOD 1
evidence of choosing sine rule (M1)
eg \(\frac{{\sin A}}{a} = \frac{{\sin B}}{b}\) , \(\frac{{\sin {\rm{A}}\widehat {\rm{C}}{\rm{D}}}}{{{\rm{AD}}}} = \frac{{\sin D}}{{{\rm{AC}}}}\)
correct substitution A1
eg \(\frac{{\sin {\rm{A}}\hat {\rm{C}}{\rm{D}}}}{8} = \frac{{\sin 104}}{{15.516 \ldots }}\)
\({\rm{A}}\hat {\rm{C}}{\rm{D}} = {30.0^ \circ }\) A1 N2
METHOD 2
evidence of choosing cosine rule (M1)
eg \({c^2} = {a^2} + {b^2} – 2ab\cos C\)
correct substitution A1
e.g. \({8^2} = {11.5^2} + 15.516{ \ldots ^2} – 2(11.5)(15.516 \ldots )\cos C\)
\({\rm{A}}\hat {\rm{C}}{\rm{D}} = {30.0^ \circ }\) A1 N2
(ii) subtracting their \({\rm{A}}\hat {\rm{C}}{\rm{D}}\) from \(73\) (M1)
eg \({\rm{7}}3 – {\rm{A}}\hat {\rm{C}}{\rm{D}}\) , \(70 – 30.017 \ldots \)
\({\rm{A}}\hat {\rm{C}}{\rm{B}} = {43.0^ \circ }\) A1 N2
[5 marks]
correct substitution (A1)
eg area \(\Delta {\rm{ADC}} = \frac{1}{2}(8)(11.5)\sin 104\)
area \( = 44.6\) (m2) A1 N2
[2 marks]
(c) correct substitution (A1)
eg area \(\Delta {\rm{ADC}} = \frac{1}{2}(8)(11.5)\sin 104\)
area \( = 44.6\) (m2) A1 N2
[2 marks]
(d) attempt to subtract (M1)
eg \({\rm{circle}} – {\rm{ABCD}}\) , \(\pi {r^2} – \Delta {\rm{ADC}} – \Delta {\rm{ACB}}\)
area \(\Delta {\rm{ACB = }}\frac{1}{2}(15.516 \ldots )(14)\sin 42.98\) (A1)
correct working A1
eg \(\pi {(8)^2} – 44.6336 \ldots – \frac{1}{2}(15.516 \ldots )(14)\sin 42.98\) , \(64\pi – 44.6 – 74.1\)
shaded area is \(82.4\) (m2) A1 N3
[4 marks]
Total [6 marks]
attempt to subtract (M1)
eg \({\rm{circle}} – {\rm{ABCD}}\) , \(\pi {r^2} – \Delta {\rm{ADC}} – \Delta {\rm{ACB}}\)
area \(\Delta {\rm{ACB = }}\frac{1}{2}(15.516 \ldots )(14)\sin 42.98\) (A1)
correct working A1
eg \(\pi {(8)^2} – 44.6336 \ldots – \frac{1}{2}(15.516 \ldots )(14)\sin 42.98\) , \(64\pi – 44.6 – 74.1\)
shaded area is \(82.4\) (m2) A1 N3
[4 marks]
Total [6 marks]
Question
The following diagram shows a triangle ABC.
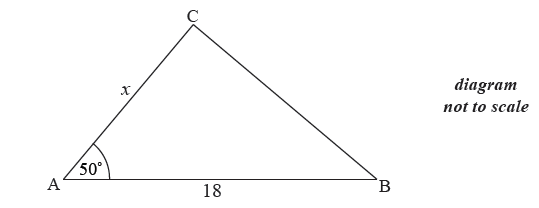
The area of triangle ABC is \(80\) cm2 , AB \( = 18\) cm , AC \( = x\) cm and \({\rm{B}}\hat {\rm{A}}{\rm{C}} = {50^ \circ }\) .
Find \(x\) .
Find BC.
Answer/Explanation
Markscheme
correct substitution into area formula (A1)
eg \(\frac{1}{2}(18x)\sin 50\)
setting their area expression equal to \(80\) (M1)
eg \(9x\sin 50 = 80\)
\(x = 11.6\) A1 N2
[3 marks]
evidence of choosing cosine rule (M1)
eg \({c^2} = {a^2} + {b^2} + 2ab\sin C\)
correct substitution into right hand side (may be in terms of \(x\)) (A1)
eg \({11.6^2} + {18^2} – 2(11.6)(18)\cos 50\)
BC \( = 13.8\) A1 N2
[3 marks]
Question
Consider a circle with centre \(\rm{O}\) and radius \(7\) cm. Triangle \(\rm{ABC}\) is drawn such that its vertices are on the circumference of the circle.
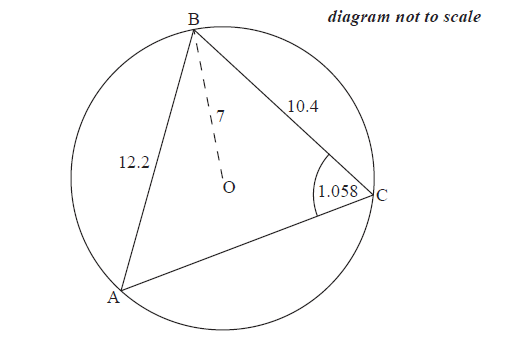
\(\rm{AB}=12.2\) cm, \(\rm{BC}=10.4\) cm and \(\rm{A}\hat{\rm{C}}\rm{B}=1.058\) radians.
Find \({\rm{B\hat AC}}\).
Find \({\text{AC}}\).
Hence or otherwise, find the length of arc \({\text{ABC}}\).
Answer/Explanation
Markscheme
Notes: In this question, there may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
Candidates may have their GDCs in degree mode, leading to incorrect answers. If working shown, award marks in line with the markscheme, with FT as appropriate.
Ignore missing or incorrect units.
evidence of choosing sine rule (M1)
eg \(\frac{{\sin \hat A}}{a} = \frac{{\sin \hat B}}{b}\)
correct substitution (A1)
eg \(\frac{{\sin \hat A}}{{10.4}} = \frac{{\sin 1.058}}{{12.2}}\)
\({\rm{B\hat AC}} = 0.837\) A1 N2
[3 marks]
Notes: In this question, there may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
Candidates may have their GDCs in degree mode, leading to incorrect answers. If working shown, award marks in line with the markscheme, with FT as appropriate.
Ignore missing or incorrect units.
METHOD 1
evidence of subtracting angles from \(\pi \) (M1)
eg \({\rm{A\hat BC}} = \pi – A – C\)
correct angle (seen anywhere) A1
\({\rm{A\hat BC}} = \pi – 1.058 – 0.837,{\text{ }}1.246,{\text{ }}71.4^\circ \)
attempt to substitute into cosine or sine rule (M1)
correct substitution (A1)
eg \({12.2^2} + {10.4^2} – 2 \times 12.2 \times 10.4\cos 71.4,{\text{ }}\frac{{{\text{AC}}}}{{\sin 1.246}} = \frac{{12.2}}{{\sin 1.058}}\)
\({\text{AC}} = 13.3{\text{ (cm)}}\) A1 N3
METHOD 2
evidence of choosing cosine rule M1
eg \({a^2} = {b^2} + {c^2} – 2bc\cos A\)
correct substitution (A2)
eg \({12.2^2} = {10.4^2} + {b^2} – 2 \times 10.4b\cos 1.058\)
\({\text{AC}} = 13.3{\text{ (cm)}}\) A2 N3
[5 marks]
Notes: In this question, there may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
Candidates may have their GDCs in degree mode, leading to incorrect answers. If working shown, award marks in line with the markscheme, with FT as appropriate.
Ignore missing or incorrect units.
METHOD 1
valid approach (M1)
eg \(\cos {\rm{A\hat OC}} = \frac{{{\text{O}}{{\text{A}}^2} + {\text{O}}{{\text{C}}^2} – {\text{A}}{{\text{C}}^2}}}{{2 \times {\text{OA}} \times {\text{OC}}}}\), \({\rm{A\hat OC}} = 2 \times {\rm{A\hat BC}}\)
correct working (A1)
eg \({\text{13.}}{{\text{3}}^2} = {7^2} + {7^2} – 2 \times 7 \times 7\cos {\rm{A\hat OC}},{\text{ }}O = 2 \times 1.246\)
\({\rm{A\hat OC}} = 2.492{\text{ }}(142.8^\circ )\) (A1)
EITHER
correct substitution for arc length (seen anywhere) A1
eg \(2.492 = \frac{l}{7},{\text{ }}l = 17.4,{\text{ }}14\pi \times \frac{{142.8}}{{360}}\)
subtracting arc from circumference (M1)
eg \(2\pi r – l,{\text{ }}14\pi = 17.4\)
OR
attempt to find \({\rm{A\hat OC}}\) reflex (M1)
eg \(2\pi – 2.492,{\text{ }}3.79,{\text{ }}360 – 142.8\)
correct substitution for arc length (seen anywhere) A1
eg \(l = 7 \times 3.79,{\text{ }}14\pi \times \frac{{217.2}}{{360}}\)
THEN
\({\text{arc ABC}} = 26.5\) A1 N4
METHOD 2
valid approach to find \({\rm{A\hat OB}}\) or \({\rm{B\hat OC}}\) (M1)
eg choosing cos rule, twice angle at circumference
correct working for finding one value, \({\rm{A\hat OB}}\) or \({\rm{B\hat OC}}\) (A1)
eg \(\cos {\rm{A\hat OB}} = \frac{{{7^2} + {7^2} – {{12.2}^2}}}{{2 \times 7 \times 7}}\), \({\rm{A\hat OB}} = 2.116,{\rm{B\hat OC}} = 1.6745\)
two correct calculations for arc lengths
eg \({\text{AB}} = 7 \times 2 \times 1.058{\text{ }}( = 14.8135),{\text{ }}7 \times 1.6745{\text{ }}( = 11.7216)\) (A1)(A1)
adding their arc lengths (seen anywhere)
eg \(r{\rm{A\hat OB}} + r{\rm{B\hat OC}},{\text{ }}14.8135 + 11.7216,{\text{ }}7(2.116 + 1.6745)\) M1
\({\text{arc ABC}} = 26.5{\text{ (cm)}}\) A1 N4
Note: Candidates may work with other interior triangles using a similar method. Check calculations carefully and award marks in line with markscheme.
[6 marks]
Question
The following diagram shows triangle ABC.
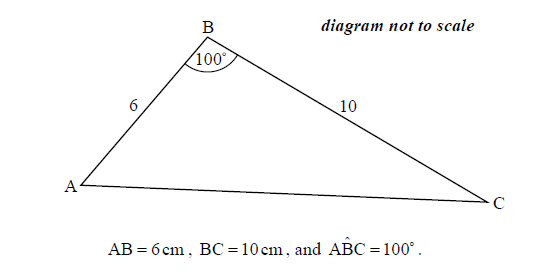
Find AC.
Find \({\rm{B\hat CA}}\).
Answer/Explanation
Markscheme
evidence of choosing cosine rule (M1)
eg \({\text{A}}{{\text{C}}^2} = {\text{A}}{{\text{B}}^2} + {\text{B}}{{\text{C}}^2} – 2({\text{AB}})({\text{BC}})\cos ({\rm{A\hat BC}})\)
correct substitution into the right-hand side (A1)
eg \({6^2} + {10^2} – 2(6)(10)\cos {100^ \circ }\)
\({\text{AC}} = 12.5234\)
\({\text{AC}} = 12.5{\text{ (cm)}}\) A1 N2
[3 marks]
evidence of choosing a valid approach (M1)
eg sine rule, cosine rule
correct substitution (A1)
eg \(\frac{{\sin ({\rm{B\hat CA)}}}}{6} = \frac{{\sin 100^\circ }}{{12.5}},{\text{ }}\cos ({\rm{B\hat CA)}} = \frac{{{{({\text{AC}})}^2} + {{10}^2} – {6^2}}}{{2({\text{AC}})(10)}}\)
\({\rm{B\hat CA}} = 28.1525\)
\({\rm{B\hat CA}} = 28.2^\circ\) A1 N2
[3 marks]
Question
In triangle \(\rm{ABC}\), \(\rm{AB} = 6\,\rm{cm}\) and \(\rm{AC} = 8\,\rm{cm}\). The area of the triangle is \(16\,\rm{cm}^2\).
Find the two possible values for \(\hat A\).
Given that \(\hat A\) is obtuse, find \({\text{BC}}\).
Answer/Explanation
Markscheme
correct substitution into area formula (A1)
eg \(\frac{1}{2}(6)(8)\sin A = 16,{\text{ }}\sin A = \frac{{16}}{{24}}\)
correct working (A1)
eg \(A = \arcsin \left( {\frac{2}{3}} \right)\)
\(A = 0.729727656…, 2.41186499…\); \((41.8103149^\circ, 138.1896851^\circ)\)
\(A = 0.730\); \(2.41\) A1A1 N3
(accept degrees ie \(41.8^\circ\); \(138^\circ\))
[4 marks]
evidence of choosing cosine rule (M1)
eg \({\text{B}}{{\text{C}}^2} = {\text{A}}{{\text{B}}^2} + {\text{A}}{{\text{C}}^2} – 2({\text{AB)(AC)}}\cos A,{\text{ }}{a^2} + {b^2} – 2ab\cos C\)
correct substitution into RHS (angle must be obtuse) (A1)
eg \({\text{B}}{{\text{C}}^2} = {6^2} + {8^2} – 2(6)(8)\cos 2.41,{\text{ }}{6^2} + {8^2} – 2(6)(8)\cos 138^\circ \),
\({\text{BC}} = \sqrt {171.55} \)
\({\text{BC}} = 13.09786\)
\({\text{BC}} = 13.1{\text{ cm}}\) A1 N2
[3 marks]
Examiners report
[N/A]
[N/A]
Question
The following diagram shows a circle with centre \(O\) and radius \(8\) cm.
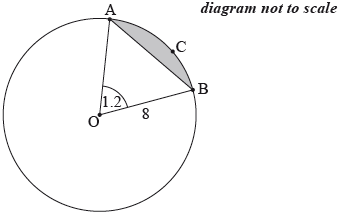
The points \(A\), \(B\) and \(C\) are on the circumference of the circle, and \({\rm{A\hat OB}}\) radians.
Find the length of arc \(ACB\).
Find \(AB\).
Hence, find the perimeter of the shaded segment \(ABC\).
Answer/Explanation
Markscheme
correct substitution into formula (A1)
eg\(\;\;\;\)\(l = 1.2 \times 8\)
\(9.6{\text{ (cm)}}\) A1 N2
[2 marks]
METHOD 1
evidence of choosing cosine rule (M1)
eg\(\;\;\;\)\(2{r^2} – 2 \times {r^2} \times \cos ({\rm{A\hat OB)}}\)
correct substitution into right hand side (A1)
eg\(\;\;\;\)\({8^2} + {8^2} – 2 \times 8 \times 8 \times \cos (1.2)\)
\(9.0342795\)
\({\text{AB}} = 9.03{\text{ }}[9.03,{\text{ }}9.04]{\text{ (cm)}}\) A1 N2
METHOD 2
evidence of choosing sine rule (M1)
eg\(\;\;\;\)\(\frac{{{\text{AB}}}}{{\sin ({\rm{A\hat OB)}}}} = \frac{{{\text{OB}}}}{{\sin ({\rm{O\hat AB)}}}}\)
finding angle \(OAB\) or \(OBA\) (may be seen in substitution) (A1)
eg\(\;\;\;\)\(\frac{{\pi – 1.2}}{2},{\text{ }}0.970796\)
\({\text{AB}} = 9.03{\text{ }}[9.03,{\text{ }}9.04]{\text{ (cm)}}\) A1 N2
[3 marks]
correct working (A1)
eg\(\;\;\;\)\(P = 9.6 + 9.03\)
\(18.6342\)
\(18.6{\text{ }}[18.6,{\text{ }}18.7]{\text{ (cm)}}\) A1 N2
[2 marks]
Total [7 marks]
Question
The following diagram shows a square \(ABCD\), and a sector \(OAB\) of a circle centre \(O\), radius \(r\). Part of the square is shaded and labelled \(R\).
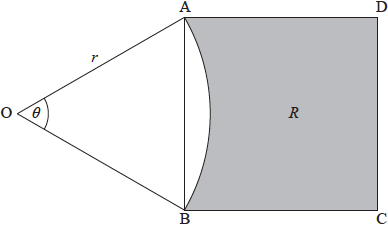
\[{\rm{A\hat OB}} = \theta {\text{, where }}0.5 \ \le \ \theta < \pi .\]
Show that the area of the square \(ABCD\) is \(2{r^2}(1 – \cos \theta )\).
When \(\theta = \alpha \), the area of the square \(ABCD\) is equal to the area of the sector \(OAB\).
(i) Write down the area of the sector when \(\theta = \alpha \).
(ii) Hence find \(\alpha \).
When \(\theta = \beta \), the area of \(R\) is more than twice the area of the sector.
Find all possible values of \(\beta \).
Answer/Explanation
Markscheme
area of \({\text{ABCD}} = {\text{A}}{{\text{B}}^2}\) (seen anywhere) (A1)
choose cosine rule to find a side of the square (M1)
eg\(\;\;\;{a^2} = {b^2} + {c^2} – 2bc\cos \theta \)
correct substitution (for triangle \(AOB\)) A1
eg\(\;\;\;{r^2} + {r^2} – 2 \times r \times r\cos \theta ,{\text{ O}}{{\text{A}}^2} + {\text{O}}{{\text{B}}^2} – 2 \times {\text{OA}} \times {\text{OB}}\cos \theta \)
correct working for \({\text{A}}{{\text{B}}^2}\) A1
eg\(\;\;\;2{r^{\text{2}}} – 2{r^2}\cos \theta \)
\({\text{area}} = 2{r^2}(1 – \cos \theta )\) AG N0
Note: Award no marks if the only working is \(2{r^2} – 2{r^2}\cos \theta \).
[4 marks]
(i) \(\frac{1}{2}\alpha {r^2}\;\;\;\left( {{\text{accept }}2{r^2}(1 – \cos \alpha )} \right)\) A1 N1
(ii) correct equation in one variable (A1)
eg\(\;\;\;2(1 – \cos \alpha ) = \frac{1}{2}\alpha \)
\(\alpha = 0.511024\)
\(\alpha = 0.511\;\;\;({\text{accept }}\theta = 0.511)\) A2 N2
Note: Award A1 for \(\alpha = 0.511\) and additional answers.
[4 marks]
Note: In this part, accept \(\theta \) instead of \(\beta \), and the use of equations instead of inequalities in the working.
attempt to find \(R\) (M1)
eg\(\;\;\;\)subtraction of areas, \({\text{square}} – {\text{segment}}\)
correct expression for segment area (A1)
eg\(\;\;\;\frac{1}{2}\beta {r^2} – \frac{1}{2}{r^2}\sin \beta \)
correct expression for \(R\) (A1)
eg\(\;\;\;2{r^2}(1 – \cos \beta ) – \left( {\frac{1}{2}\beta {r^2} – \frac{1}{2}{r^2}\sin \beta } \right)\)
correct inequality (A1)
eg\(\;\;\;2{r^2}(1 – \cos \beta ) – \left( {\frac{1}{2}\beta {r^2} – \frac{1}{2}{r^2}\sin \beta } \right) > 2\left( {\frac{1}{2}\beta {r^2}} \right)\)
correct inequality in terms of angle only A1
eg\(\;\;\;2(1 – \cos \beta ) – \left( {\frac{1}{2}\beta – \frac{1}{2}\sin \beta } \right) > \beta \)
attempt to solve their inequality, must represent \(R > \) twice sector (M1)
eg\(\;\;\;\)sketch, one correct value
Note: Do not award the second (M1) unless the first (M1) for attempting to find \(R\) has been awarded.
both correct values \(1.30573\) and \(2.67369\) (A1)
correct inequality \(1.31 < \beta < 2.67\) A1 N3
[8 marks]
Total [16 marks]
Question
The following diagram shows the quadrilateral \(ABCD\).
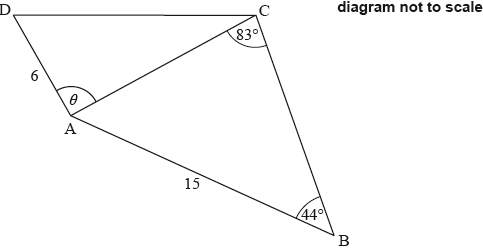
\[{\text{AD}} = 6{\text{ cm}},{\text{ AB}} = 15{\text{ cm}},{\rm{ A\hat BC}} = 44^\circ ,{\rm{ A\hat CB}} = 83^\circ {\rm{ and D\hat AC}} = \theta \]
Find \(AC\).
Find the area of triangle \(ABC\).
The area of triangle \(ACD\) is half the area of triangle \(ABC\).
Find the possible values of \(\theta \).
Given that \(\theta \) is obtuse, find \(CD\).
Answer/Explanation
Markscheme
evidence of choosing sine rule (M1)
eg\(\;\;\;\frac{{{\text{AC}}}}{{\sin {\rm{C\hat BA}}}} = \frac{{{\text{AB}}}}{{\sin {\rm{A\hat CB}}}}\)
correct substitution (A1)
eg\(\;\;\;\frac{{{\text{AC}}}}{{\sin 44^\circ }} = \frac{{15}}{{\sin 83^\circ }}\)
\(10.4981\)
\({\text{AC}} = 10.5{\text{ }}{\text{ (cm)}}\) A1 N2
[3 marks]
finding \({\rm{C\hat AB}}\) (seen anywhere) (A1)
eg\(\;\;\;180^\circ – 44^\circ – 83^\circ ,{\rm{ C\hat AB}} = 53^\circ \)
correct substitution for area of triangle \(ABC\) A1
eg\(\;\;\;\frac{1}{2} \times 15 \times 10.4981 \times \sin 53^\circ \)
62.8813
\({\text{area}} = 62.9{\text{ }}{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1 N2
[3 marks]
correct substitution for area of triangle \(DAC\) (A1)
eg\(\;\;\;\frac{1}{2} \times 6 \times 10.4981 \times \sin \theta \)
attempt to equate area of triangle \(ACD\) to half the area of triangle \(ABC\) (M1)
eg\(\;\;\;{\text{area ACD}} = \frac{1}{2} \times {\text{ area ABC; 2ACD}} = {\text{ABC}}\)
correct equation A1
eg\(\;\;\;\frac{1}{2} \times 6 \times 10.4981 \times \sin \theta = \frac{1}{2}(62.9),{\text{ }}62.9887\sin \theta = 62.8813,{\text{ }}\sin \theta = 0.998294\)
\(86.6531\), \(93.3468\)
\(\theta = 86.7^\circ {\text{ }},{\text{ }}\theta = 93.3^\circ {\text{ }}\) A1A1 N2
[5 marks]
Note: Note: If candidates use an acute angle from part (c) in the cosine rule, award M1A0A0 in part (d).
evidence of choosing cosine rule (M1)
eg\(\;\;\;{\text{C}}{{\text{D}}^2} = {\text{A}}{{\text{D}}^2} + {\text{A}}{{\text{C}}^2} – 2 \times {\text{AD}} \times {\text{AC}} \times \cos \theta \)
correct substitution into rhs (A1)
eg\(\;\;\;{\text{C}}{{\text{D}}^2} = {6^2} + {10.498^2} – 2(6)(10.498)\cos 93.336^\circ \)
\(12.3921\)
\(12.4{\text{ }}{\text{ (cm)}}\) A1 N2
[3 marks]
Total [14 marks]
Question
The following diagram shows three towns A, B and C. Town B is 5 km from Town A, on a bearing of 070°. Town C is 8 km from Town B, on a bearing of 115°.
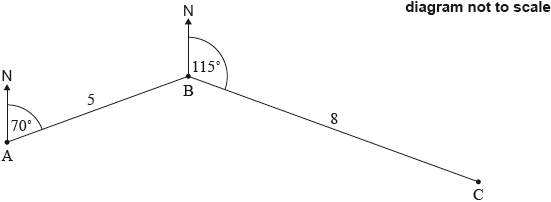
Find \({\rm{A\hat BC}}\).
Find the distance from Town A to Town C.
Use the sine rule to find \({\rm{A\hat CB}}\).
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\(70 + (180 – 115),{\text{ }}360 – (110 + 115)\)
\({\rm{A\hat BC}} = 135^\circ \) A1 N2
[2 marks]
choosing cosine rule (M1)
eg\(\,\,\,\,\,\)\({c^2} = {a^2} + {b^2} – 2ab\cos C\)
correct substitution into RHS (A1)
eg\(\,\,\,\,\,\)\({5^2} + {8^2} – 2 \times 5 \times 8\cos 135\)
12.0651
12.1 (km) A1 N2
[3 marks]
correct substitution (must be into sine rule) A1
eg\(\,\,\,\,\,\)\(\frac{{\sin {\rm{A\hat CB}}}}{5} = \frac{{\sin 135}}{{{\text{AC}}}}\)
17.0398
\({\rm{A\hat CB}} = 17.0\) A1 N1
[2 marks]
Question
The following diagram shows a quadrilateral ABCD.
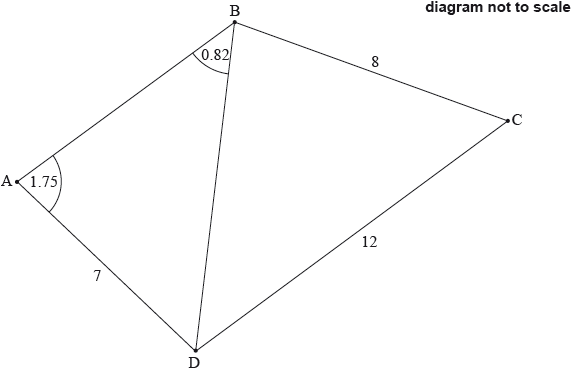
\[{\text{AD}} = {\text{7}}\;{\text{cm,}}\;{\text{BC}} = {\text{8}}\;{\text{cm,}}\;{\text{CD}} = {\text{12}}\;{\text{cm,}}\;{\rm{D\hat AB}} = {\text{1.75}}\;{\text{radians,}}\;{\rm{A\hat BD}} = {\text{0.82}}\;{\text{radians.}}\]
Find BD.
Find \({\rm{D\hat BC}}\).
Answer/Explanation
Markscheme
evidence of choosing sine rule (M1)
eg\(\,\,\,\,\,\)\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(\frac{a}{{\sin 1.75}} = \frac{7}{{\sin 0.82}}\)
9.42069
\({\text{BD}} = 9.42{\text{ (cm)}}\) A1 N2
[3 marks]
evidence of choosing cosine rule (M1)
eg\(\,\,\,\,\,\)\(\cos B = \frac{{{d^2} + {c^2} – {b^2}}}{{2dc}},{\text{ }}{a^2} = {b^2} + {c^2} – 2bc\cos B\)
correct substitution (A1)
eg\(\,\,\,\,\,\)\(\frac{{{8^2} + {{9.42069}^2} – {{12}^2}}}{{2 \times 8 \times 9.42069}},{\text{ }}144 = 64 + {\text{B}}{{\text{D}}^2} – 16{\text{BD}}\cos B\)
1.51271
\({\rm{D\hat BC}} = 1.51\) (radians) (accept 86.7°) A1 N2
[3 marks]
Question
The following diagram shows a circle, centre O and radius \(r\) mm. The circle is divided into five equal sectors.
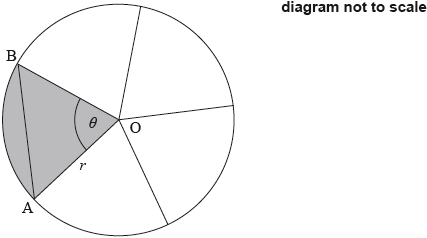
One sector is OAB, and \({\rm{A\hat OB}} = \theta \).
The area of sector AOB is \(20\pi {\text{ m}}{{\text{m}}^2}\).
Write down the exact value of \(\theta \) in radians.
Find the value of \(r\).
Find AB.
Answer/Explanation
Markscheme
\(\theta = \frac{{2\pi }}{5}\) A1 N1
[1 mark]
correct expression for area (A1)
eg\(\,\,\,\,\,\)\(A = \frac{1}{2}{r^2}\left( {\frac{{2\pi }}{5}} \right),{\text{ }}\frac{{\pi {r^2}}}{5}\)
evidence of equating their expression to \(20\pi \) (M1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}{r^2}\left( {\frac{{2\pi }}{5}} \right) = 20\pi ,{\text{ }}{r^2} = 100,{\text{ }}r = \pm 10\)
\(r = 10\) A1 N2
[3 marks]
METHOD 1
evidence of choosing cosine rule (M1)
eg\(\,\,\,\,\,\)\({a^2} = {b^2} + {c^2} – 2bc\cos A\)
correct substitution of their \(r\) and \(\theta \) into RHS (A1)
eg\(\,\,\,\,\,\)\({10^2} + {10^2} – 2 \times 10 \times 1{\text{0}}\cos \left( {\frac{{2\pi }}{5}} \right)\)
11.7557
\({\text{AB}} = 11.8{\text{ (mm)}}\) A1 N2
METHOD 2
evidence of choosing sine rule (M1)
eg\(\,\,\,\,\,\)\(\frac{{\sin A}}{a} = \frac{{\sin B}}{b}\)
correct substitution of their \(r\) and \(\theta \) (A1)
eg\(\,\,\,\,\,\)\(\frac{{\sin \frac{{2\pi }}{5}}}{{{\text{AB}}}} = \frac{{\sin \left( {\frac{1}{2}\left( {\pi – \frac{{2\pi }}{5}} \right)} \right)}}{{10}}\)
11.7557
\({\text{AB}} = 11.8{\text{ (mm)}}\) A1 N2
[3 marks]
Question
The following diagram shows the chord [AB] in a circle of radius 8 cm, where \({\text{AB}} = 12{\text{ cm}}\).
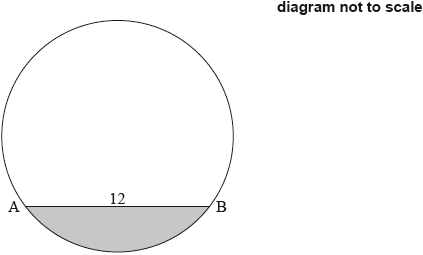
Find the area of the shaded segment.
Answer/Explanation
Markscheme
attempt to find the central angle or half central angle (M1)
eg\(\,\,\,\,\,\)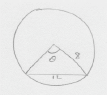
, cosine rule, right triangle
correct working (A1)
eg\(\,\,\,\,\,\)\(\cos \theta = \frac{{{8^2} + {8^2} – {{12}^2}}}{{2 \bullet 8 \bullet 8}},{\text{ }}{\sin ^{ – 1}}\left( {\frac{6}{8}} \right),{\text{ }}0.722734,{\text{ }}41.4096^\circ ,{\text{ }}\frac{\pi }{2} – {\sin ^{ – 1}}\left( {\frac{6}{8}} \right)\)
correct angle \({\rm{A\hat OB}}\) (seen anywhere)
eg\(\,\,\,\,\,\)\({\text{1.69612, }}97.1807^\circ ,{\text{ 2}} \times {\text{si}}{{\text{n}}^{ – 1}}\left( {\frac{6}{8}} \right)\) (A1)
correct sector area
eg\(\,\,\,\,\,\)\(\frac{1}{2}(8)(8)(1.70),{\text{ }}\frac{{97.1807}}{{360}}(64\pi ),{\text{ }}54.2759\) (A1)
area of triangle (seen anywhere) (A1)
eg\(\,\,\,\,\,\)\(\frac{1}{2}(8)(8)\sin 1.70,{\text{ }}\frac{1}{2}(8)(12)\sin 0.722,{\text{ }}\frac{1}{2} \times \sqrt {64 – 36} \times 12,{\text{ }}31.7490\)
appropriate approach (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\({A_{{\text{triangle}}}} – {A_{{\text{sector}}}}\), their sector-their triangle
22.5269
area of shaded region \( = 22.5{\text{ }}({\text{c}}{{\text{m}}^2})\) A1 N4
Note: Award M0A0A0A0A1 then M1A0 (if appropriate) for correct triangle area without any attempt to find an angle in triangle OAB.
[7 marks]
Question
A ship is sailing north from a point A towards point D. Point C is 175 km north of A. Point D is 60 km north of C. There is an island at E. The bearing of E from A is 055°. The bearing of E from C is 134°. This is shown in the following diagram.
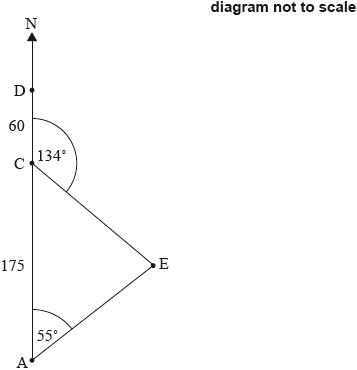
Find the bearing of A from E.
Finds CE.
Find DE.
When the ship reaches D, it changes direction and travels directly to the island at 50 km per hour. At the same time as the ship changes direction, a boat starts travelling to the island from a point B. This point B lies on (AC), between A and C, and is the closest point to the island. The ship and the boat arrive at the island at the same time. Find the speed of the boat.
Answer/Explanation
Markscheme
valid method (M1)
eg\(\,\,\,\,\,\)\(180 + 55,{\text{ }}360 – 90 – 35\)
235° (accept S55W, W35S) A1 N2
[2 marks]
valid approach to find \({\rm{A\hat EC}}\) (may be seen in (a)) (M1)
eg\(\,\,\,\,\,\)\({\rm{A\hat EC}} = 180 – 55 – {\rm{A\hat CE}},{\text{ }}134 = {\text{E}} + 55\)
correct working to find \({\rm{A\hat EC}}\) (may be seen in (a)) (A1)
eg\(\,\,\,\,\,\)\(180 – 55 – 46,{\text{ }}134 – 55\), \({\rm{A\hat EC}} = 79^\circ \)
evidence of choosing sine rule (seen anywhere) (M1)
eg\(\,\,\,\,\,\)\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\)
correct substitution into sine rule (A1)
eg\(\,\,\,\,\,\)\(\frac{{{\text{CE}}}}{{\sin 55^\circ }} = \frac{{175}}{{\sin {\rm{A\hat EC}}}}\)
146.034
\({\text{CE}} = 146{\text{ (km)}}\) A1 N2
[5 marks]
evidence of choosing cosine rule (M1)
eg\(\,\,\,\,\,\)\({\text{D}}{{\text{E}}^2} = {\text{D}}{{\text{C}}^2} + {\text{C}}{{\text{E}}^2} – 2 \times {\text{DC}} \times {\text{CE}} \times \cos \theta \)
correct substitution into right-hand side (A1)
eg\(\,\,\,\,\,\)\({60^2} + {146.034^2} – 2 \times 60 \times 146.034\cos 134\)
192.612
\({\text{DE}} = 193{\text{ (km)}}\) A1 N2
[3 marks]
valid approach for locating B (M1)
eg\(\,\,\,\,\,\)BE is perpendicular to ship’s path, angle \({\text{B}} = 90\)
correct working for BE (A1)
eg\(\,\,\,\,\,\)\(\sin 46^\circ = \frac{{{\text{BE}}}}{{146.034}},{\text{ BE}} = 146.034\sin 46^\circ ,{\text{ }}105.048\)
valid approach for expressing time (M1)
eg\(\,\,\,\,\,\)\(t = \frac{d}{s},{\text{ }}t = \frac{d}{r},{\text{ }}t = \frac{{192.612}}{{50}}\)
correct working equating time (A1)
eg\(\,\,\,\,\,\)\(\frac{{146.034\sin 46^\circ }}{r} = \frac{{192.612}}{{50}},{\text{ }}\frac{s}{{105.048}} = \frac{{50}}{{192.612}}\)
27.2694
27.3 (km per hour) A1 N3
[5 marks]
Question
Triangle ABC has a = 8.1 cm, b = 12.3 cm and area 15 cm2. Find the largest possible perimeter of triangle ABC.
Answer/Explanation
Markscheme
correct substitution into the formula for area of a triangle (A1)
eg 15 = \(\frac{1}{2}\) × 8.1 × 12.3 × sin C
correct working for angle C (A1)
eg sin C = 0.301114, 17.5245…, 0.305860
recognizing that obtuse angle needed (M1)
eg 162.475, 2.83573, cos C < 0
evidence of choosing the cosine rule (M1)
eg a2 = b2 + c2 − 2bc cos(A)
correct substitution into cosine rule to find c (A1)
eg c2 = (8.1)2 + (12.3)2 − 2(8.1)(12.3) cos C
c = 20.1720 (A1)
8.1 + 12.3 + 20.1720 = 40.5720
perimeter = 40.6 A1 N4
[7 marks]
Question
The following diagram shows quadrilateral ABCD.
\({\text{AB}} = 11\,{\text{cm,}}\,\,{\text{BC}} = 6\,{\text{cm,}}\,\,{\text{B}}\mathop {\text{A}}\limits^ \wedge {\text{D = 100}}^\circ {\text{, and C}}\mathop {\text{B}}\limits^ \wedge {\text{D = 82}}^\circ \)
Find DB.
Find DC.
Answer/Explanation
Markscheme
evidence of choosing sine rule (M1)
eg \(\frac{a}{{{\text{sin }}A}} = \frac{b}{{{\text{sin }}B}} = \frac{c}{{{\text{sin }}C}}\)
correct substitution (A1)
eg \(\frac{{{\text{DB}}}}{{{\text{sin }}59^\circ }} = \frac{{{\text{11}}}}{{{\text{sin }}100^\circ }}\)
9.57429
DB = 9.57 (cm) A1 N2
[3 marks]
evidence of choosing cosine rule (M1)
eg \({a^2} = {b^2} + {c^2} – 2bc\,\,{\text{cos}}\,\,\left( A \right),\,\,\,{\text{D}}{{\text{C}}^2} = \,\,{\text{D}}{{\text{B}}^2}{\text{ + B}}{{\text{C}}^2}{\text{ }} – {\text{ 2DB}} \times \,\,{\text{BC}} \times \,{\text{cos}}\,\left( {{\text{D}}\mathop {\text{B}}\limits^ \wedge {\text{C}}} \right)\)
correct substitution into RHS (A1)
eg \({9.57^2} + {6^2} – 2 \times 9.57 \times 6 \times \,\,{\text{cos}}\,\,82^\circ ,\,\,\,111.677\)
10.5677
DC = 10.6 (cm) A1 N2
[3 marks]