Question
A box contains 100 cards. Each card has a number between one and six written on it. The following table shows the frequencies for each number.

Calculate the value of k.
Find
(i) the median;
(ii) the interquartile range.
Answer/Explanation
Markscheme
evidence of using \(\sum {{f_i} = 100} \) (M1)
\(k = 4\) A1 N2
[2 marks]
(i) evidence of median position (M1)
e.g. 50th item, \(26 + 10 + 20 = 56\)
\({\text{median}} = 3\) A1 N2
(ii) \({Q_1} = 1\) and \({Q_3} = 5\) (A1)(A1)
\({\text{interquartile range}} = 4\) (accept 1 to 5 or \(5 – 1\) , etc.) A1 N3
[5 marks]
Question
The ages of people attending a music concert are given in the table below.
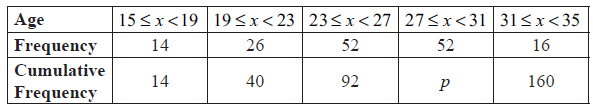
Find p .
The cumulative frequency diagram is given below.
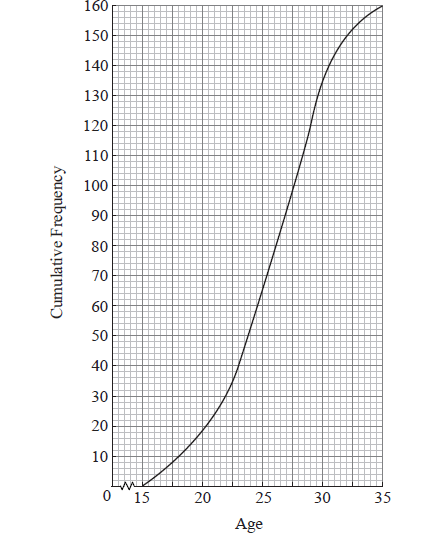
Use the diagram to estimate
(i) the 80th percentile;
(ii) the interquartile range.
Answer/Explanation
Markscheme
evidence of valid approach (M1)
e.g. \(92 + 52\) , line on graph at \(x = 31\)
\(p = 144\) A1 N2
[2 marks]
(i) evidence of valid approach (M1)
e.g. line on graph, \(0.8 \times 160\) , using complement
\( = 29.5\) A1 N2
(ii) \({Q_1} = 23\) ; \({Q_3} = 29\) (A1)(A1)
\({\text{IQR}} = 6\) (accept any notation that suggests an interval) A1 N3
[5 marks]
Question
A running club organizes a race to select girls to represent the club in a competition.
The times taken by the group of girls to complete the race are shown in the table below.
Find the value of \(p\) and of \(q\) .
A girl is chosen at random.
(i) Find the probability that the time she takes is less than \(14\) minutes.
(ii) Find the probability that the time she takes is at least \(26\) minutes.
A girl is selected for the competition if she takes less than \(x\) minutes to complete the race.
Given that \(40\%\) of the girls are not selected,
(i) find the number of girls who are not selected;
(ii) find \(x\) .
Girls who are not selected, but took less than \(25\) minutes to complete the race, are allowed another chance to be selected. The new times taken by these girls are shown in the cumulative frequency diagram below.
(i) Write down the number of girls who were allowed another chance.
(ii) Find the percentage of the whole group who were selected.
Answer/Explanation
Markscheme
attempt to find \(p\) (M1)
eg \(120 – 70\) , \(50 + 20 + x = 120\)
\(p = 50\) A1 N2
attempt to find \(q\) (M1)
eg \(180 – 20\) , \(200 – 20 – 20\)
\(q = 160\) A1 N2
[4 marks]
(i) \(\frac{{70}}{{200}}\) \(\left( { = \frac{7}{{20}}} \right)\) A1 N1
(ii) valid approach (M1)
eg \(20 + 20\) , \(200 – 160\)
\(\frac{{40}}{{200}}\) \(\left( { = \frac{1}{5}} \right)\) A1 N2
[3 marks]
(i) attempt to find number of girls (M1)
eg \(0.4\), \(\frac{{40}}{{100}} \times 200\)
\(80\) are not selected A1 N2
(ii) \(120\) are selected (A1)
\(x = 20\) A1 N2
[4 marks]
(i) \(30\) given second chance A1 N1
(ii) \(20\) took less than \(20\) minutes (A1)
attempt to find their selected total (may be seen in \(\%\) calculation) (M1)
eg \(120 + 20\) \(( = 140)\) , \(120 + \) their answer from (i)
\(70\) (\(\%\)) A1 N3
[4 marks]
Question
A school collects cans for recycling to raise money. Sam’s class has 20 students.
The number of cans collected by each student in Sam’s class is shown in the following stem and leaf diagram.
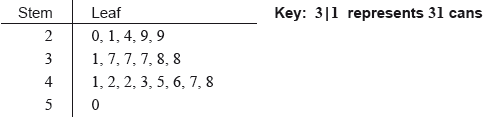
The following box-and-whisker plot also displays the number of cans collected by students in Sam’s class.

There are 80 students in the school.
The mean number of cans collected is 39.4. The standard deviation is 18.5.
Each student then collects 2 more cans.
Find the median number of cans collected.
(i) Write down the value of \(a\).
(ii) The interquartile range is 14. Find the value of \(b\).
Sam’s class collected 745 cans. They want an average of 40 cans per student.
How many more cans need to be collected to achieve this target?
The students raise $0.10 for each recycled can.
(i) Find the largest amount raised by a student in Sam’s class.
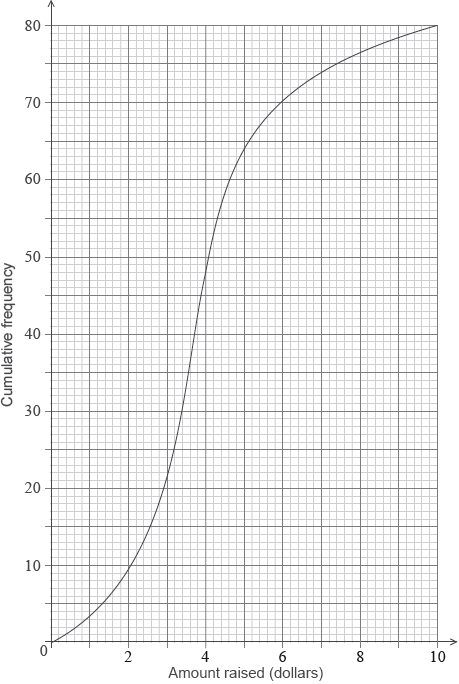
(ii) The following cumulative frequency curve shows the amounts in dollars raised by all the students in the school. Find the percentage of students in the school who raised more money than anyone in Sam’s class.
(i) Write down the new mean.
(ii) Write down the new standard deviation.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)between 10th and 11th, \(\frac{{8 + 8}}{2}\)
median \( = 38\) A1 N2
[2 marks]
(i) \(a = 20\) A1 N1
(ii) valid approach (M1)
eg\(\,\,\,\,\,\)\({Q_3} – {Q_1},{\text{ }}{Q_1} + 14,{\text{ }}b – 30 = 14\)
\(b = 44\) A1 N2
[3 marks]
valid approach (M1)
egx\(\,\,\,\,\,\)\(40 \times 20,{\text{ }}\frac{{x + 745}}{{20}},{\text{ }}40 – \frac{{745}}{{20}}\)
correct working (A1)
eg\(\,\,\,\,\,\)\(800 – 745,{\text{ }}20 \times 2.75\)
55 (more cans) A1 N2
[3 marks]
(i) most cans in Sam’s class \( = 50\) (A1)
5 ($) A1 N2
(ii) correct value of 64 or 16 A1
valid approach (M1)
eg\(\,\,\,\,\,\)\(\frac{{64}}{{80}},{\text{ }}80\% ,{\text{ }}80 – 64,{\text{ }}\frac{{16}}{{80}}\)
20% A1 N2
[5 marks]
(i) 41.4 (exact) A1 N1
(ii) 18.5 A1 N1
[2 marks]
Question
The following box-and-whisker plot shows the number of text messages sent by students in a school on a particular day.
Find the value of the interquartile range.
One student sent k text messages, where k > 11 . Given that k is an outlier, find the least value of k.
Answer/Explanation
Markscheme
recognizing Q1 or Q3 (seen anywhere) (M1)
eg 4,11 , indicated on diagram
IQR = 7 A1 N2
[2 marks]
recognizing the need to find 1.5 IQR (M1)
eg 1.5 × IQR, 1.5 × 7
valid approach to find k (M1)
eg 10.5 + 11, 1.5 × IQR + Q3
21.5 (A1)
k = 22 A1 N3
Note: If no working shown, award N2 for an answer of 21.5.
[4 marks]
