Download IITian Academy App for accessing Online Mock Tests and More..
Question
The weights in grams of 80 rats are shown in the following cumulative frequency diagram.
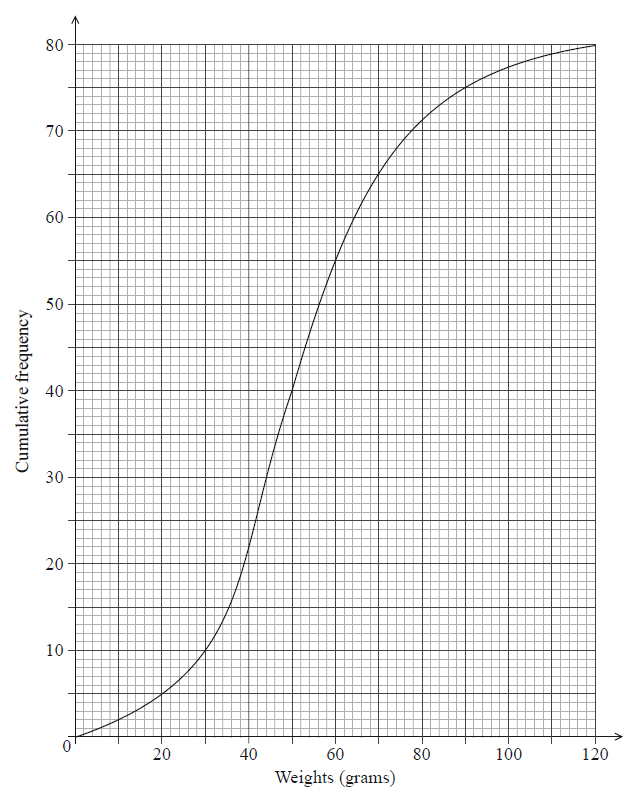
Do NOT write solutions on this page.
Write down the median weight of the rats.
Find the percentage of rats that weigh 70 grams or less.
The same data is presented in the following table.
| Weights \(w\) grams | \(0 \leqslant w \leqslant 30\) | \(30 < w \leqslant 60\) | \(60 < w \leqslant 90\) | \(90 < w \leqslant 120\) |
| Frequency | \(p\) | \(45\) | \(q\) | \(5\) |
Write down the value of \(p\).
The same data is presented in the following table.
| Weights \(w\) grams | \(0 \leqslant w \leqslant 30\) | \(30 < w \leqslant 60\) | \(60 < w \leqslant 90\) | \(90 < w \leqslant 120\) |
| Frequency | \(p\) | \(45\) | \(q\) | \(5\) |
Find the value of \(q\).
The same data is presented in the following table.
| Weights \(w\) grams | \(0 \leqslant w \leqslant 30\) | \(30 < w \leqslant 60\) | \(60 < w \leqslant 90\) | \(90 < w \leqslant 120\) |
| Frequency | \(p\) | \(45\) | \(q\) | \(5\) |
Use the values from the table to estimate the mean and standard deviation of the weights.
Assume that the weights of these rats are normally distributed with the mean and standard deviation estimated in part (c).
Find the percentage of rats that weigh 70 grams or less.
Assume that the weights of these rats are normally distributed with the mean and standard deviation estimated in part (c).
A sample of five rats is chosen at random. Find the probability that at most three rats weigh 70 grams or less.
Answer/Explanation
Markscheme
50 (g) A1 N1
[2 marks]
65 rats weigh less than 70 grams (A1)
attempt to find a percentage (M1)
eg \(\frac{{65}}{{80}},{\text{ }}\frac{{65}}{{80}} \times 100\)
81.25 (%) (exact), 81.3 A1 N3
[2 marks]
\(p = 10\) A2 N2
[2 marks]
subtracting to find \(q\) (M1)
eg \(75 – 45 – 10\)
\(q = 20\) A1 N2
[2 marks]
evidence of mid-interval values (M1)
eg \(15, 45, 75, 105\)
\(\overline x = 52.5\) (exact), \(\sigma = 22.5\) (exact) A1A1 N3
[3 marks]
0.781650
78.2 (%) A2 N2
[2 marks]
recognize binomial probability (M1)
eg \(X \sim {\text{B}}(n,{\text{ }}p)\), \(\left( \begin{array}{c}5\\r\end{array} \right)\) \( \times {0.782^r} \times {0.218^{5 – r}}\)
valid approach (M1)
eg \({\text{P}}(X \leqslant 3)\)
\(0.30067\)
\(0.301\) A1 N2
[3 marks]
Question
The following cumulative frequency graph shows the monthly income, \(I\) dollars, of \(2000\) families.
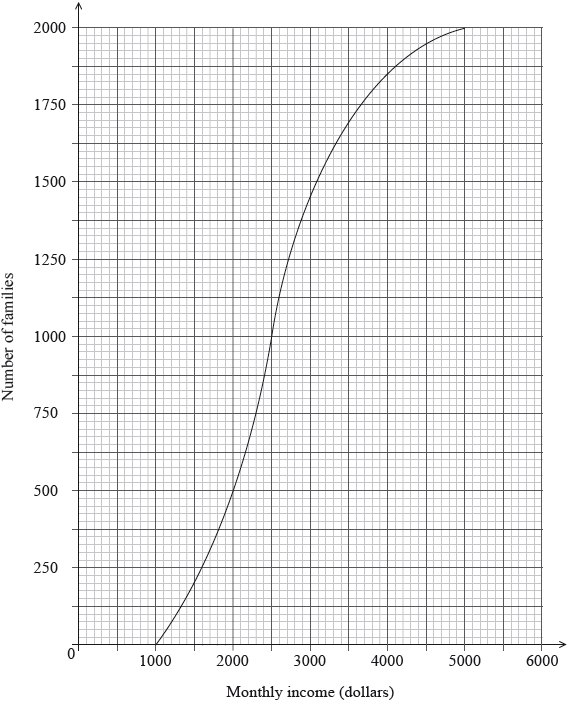
Find the median monthly income.
(i) Write down the number of families who have a monthly income of \(2000\) dollars or less.
(ii) Find the number of families who have a monthly income of more than \(4000\) dollars.
The \(2000\) families live in two different types of housing. The following table gives information about the number of families living in each type of housing and their monthly income \(I\).
Find the value of \(p\).
A family is chosen at random.
(i) Find the probability that this family lives in an apartment.
(ii) Find the probability that this family lives in an apartment, given that its monthly income is greater than \(4000\) dollars.
Estimate the mean monthly income for families living in a villa.
Answer/Explanation
Markscheme
recognizing that the median is at half the total frequency (M1)
eg\(\;\;\;\)\(\frac{{2000}}{2}\)
\(m = 2500{\text{ (dollars)}}\) A1 N2
[2 marks]
(i) \(500\) families have a monthly income less than \(2000\) A1 N1
(ii) correct cumulative frequency, \(1850\) (A1)
subtracting their cumulative frequency from \(2000\) (M1)
eg\(\;\;\;\)\(2000 – 1850\)
\(150\) families have a monthly income of more than \(4000\) dollars A1 N2
Note: If working shown, award M1A1A1 for \(128{\rm{ }} + {\rm{ }}22{\rm{ }} = {\rm{ }}150\), using the table.
[4 marks]
correct calculation (A1)
eg\(\;\;\;\)\(2000 – (436 + 64 + 765 + 28 + 122),{\text{ }}1850 – 500 – 765\) (A1)
\(p = 585\) A1 N2
[2 marks]
(i) correct working (A1)
eg\(\;\;\;\)\(436 + 765 + 28\)
\(0.6145\;\;\;\)(exact) A1 N2
\(\frac{{1229}}{{2000}},{\text{ }}0.615{\text{ }}[0.614,{\text{ }}0.615]\)
(ii) correct working/probability for number of families (A1)
eg\(\;\;\;\)\(122 + 28,{\text{ }}\frac{{150}}{{2000}},{\text{ 0.075}}\)
\(0.186666\)
\(\frac{{28}}{{150}}\;\;\;\left( { = \frac{{14}}{{75}}} \right),{\text{ }}0.187{\text{ }}[0.186,{\text{ }}0.187]\) A1 N2
[4 marks]
evidence of using correct mid-interval values (\(1500,{\rm{ }}3000,{\rm{ }}4500\)) (A1)
attempt to substitute into \(\frac{{\sum {fx} }}{{\sum f }}\) (M1)
eg\(\;\;\;\)\(\frac{{1500 \times 64 + 3000 \times p + 4500 \times 122}}{{64 + 585 + 122}}\)
\(3112.84\)
\(3110{\text{ }}[3110,{\text{ }}3120]{\text{ (dollars)}}\) A1 N2
[3 marks]
Total [15 marks]
Question
Let \(f(x) = {{\text{e}}^{0.5x}} – 2\).
For the graph of f:
(i) write down the \(y\)-intercept;
(ii) find the \(x\)-intercept;
(iii) write down the equation of the horizontal asymptote.
On the following grid, sketch the graph of \(f\), for \( – 4 \leqslant x \leqslant 4\).
Answer/Explanation
Markscheme
(i) \(y = – 1\) A1 N1
(ii) valid attempt to find \(x\)-intercept (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0\)
1.38629 A1 N2
\(x = 2\ln 2{\text{ (exact), }}1.39\)
(iii) \(y = – 2\) (must be equation) A1 N1
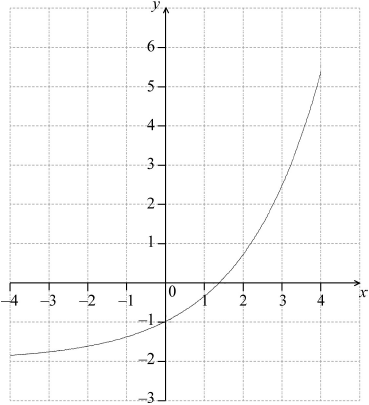A1A1A1 N3
[3 marks]
Question
Ten students were surveyed about the number of hours, \(x\), they spent browsing the Internet during week 1 of the school year. The results of the survey are given below.
\[\sum\limits_{i = 1}^{10} {{x_i} = 252,{\text{ }}\sigma = 5{\text{ and median}} = 27.} \]
During week 4, the survey was extended to all 200 students in the school. The results are shown in the cumulative frequency graph:
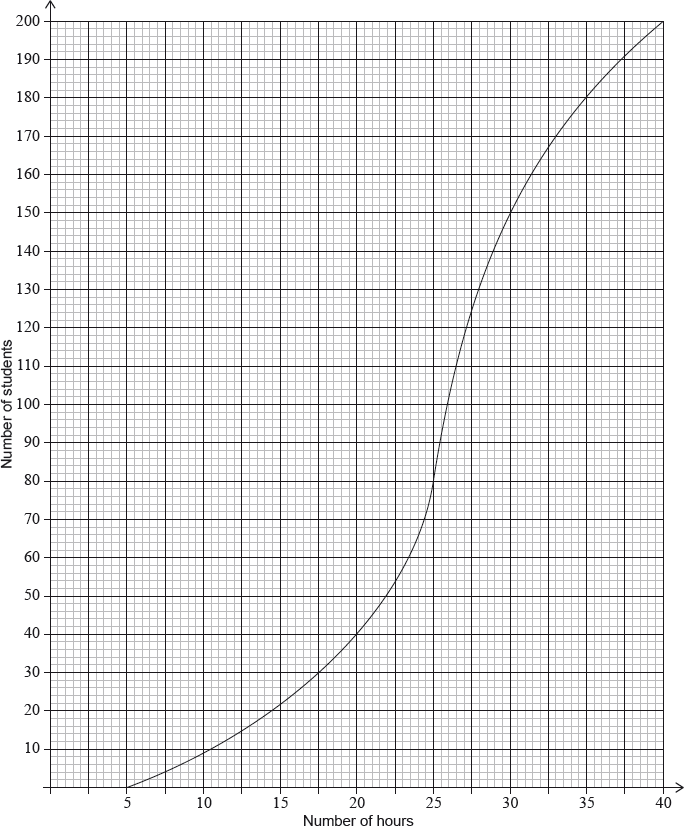
Find the mean number of hours spent browsing the Internet.
During week 2, the students worked on a major project and they each spent an additional five hours browsing the Internet. For week 2, write down
(i) the mean;
(ii) the standard deviation.
During week 3 each student spent 5% less time browsing the Internet than during week 1. For week 3, find
(i) the median;
(ii) the variance.
(i) Find the number of students who spent between 25 and 30 hours browsing the Internet.
(ii) Given that 10% of the students spent more than k hours browsing the Internet, find the maximum value of \(k\).
Answer/Explanation
Markscheme
attempt to substitute into formula for mean (M1)
eg\(\,\,\,\,\,\)\(\frac{{\Sigma x}}{{10}},{\text{ }}\frac{{252}}{n},{\text{ }}\frac{{252}}{{10}}\)
mean \( = 25.2{\text{ (hours)}}\) A1 N2
[2 marks]
(i) mean \( = 30.2{\text{ (hours)}}\) A1 N1
(ii) \(\sigma = 5{\text{ (hours)}}\) A1 N1
[2 marks]
(i) valid approach (M1)
eg\(\,\,\,\,\,\)95%, 5% of 27
correct working (A1)
eg\(\,\,\,\,\,\)\(0.95 \times 27,{\text{ }}27 – (5\% {\text{ of }}27)\)
median \( = 25.65{\text{ (exact), }}25.7{\text{ (hours)}}\) A1 N2
(ii) METHOD 1
variance \( = {({\text{standard deviation}})^2}\) (seen anywhere) (A1)
valid attempt to find new standard deviation (M1)
eg\(\,\,\,\,\,\)\({\sigma _{new}} = 0.95 \times 5,{\text{ }}4.75\)
variance \( = 22.5625{\text{ }}({\text{exact}}),{\text{ }}22.6\) A1 N2
METHOD 2
variance \( = {({\text{standard deviation}})^2}\) (seen anywhere) (A1)
valid attempt to find new variance (M1)
eg\(\,\,\,\,\,\)\({0.95^2}{\text{ }},{\text{ }}0.9025 \times {\sigma ^2}\)
new variance \( = 22.5625{\text{ }}({\text{exact}}),{\text{ }}22.6\) A1 N2
[6 marks]
(i) both correct frequencies (A1)
eg\(\,\,\,\,\,\)80, 150
subtracting their frequencies in either order (M1)
eg\(\,\,\,\,\,\)\(150 – 80,{\text{ }}80 – 150\)
70 (students) A1 N2
(ii) evidence of a valid approach (M1)
eg\(\,\,\,\,\,\)10% of 200, 90%
correct working (A1)
eg\(\,\,\,\,\,\)\(0.90 \times 200,{\text{ }}200 – 20\), 180 students
\(k = 35\) A1 N3
[6 marks]