Question
Two events \(A\) and \(B\) are such that \({\text{P}}(A) = 0.2\) and \({\text{P}}(A \cup B) = 0.5\).
Given that \(A\) and \(B\) are mutually exclusive, find \({\text{P}}(B)\).
Given that \(A\) and \(B\) are independent, find \({\text{P}}(B)\).
Answer/Explanation
Markscheme
correct approach (A1)
eg \(0.5 = 0.2 + {\text{P}}(B),{\text{ P}}(A \cap B) = 0\)
\({\text{P}}(B) = 0.3\) A1 N2
[2 marks]
Correct expression for \({\text{P}}(A \cap B)\) (seen anywhere) A1
eg \({\text{P}}(A \cap B) = 0.2{\text{P}}(B),{\text{ }}0.2x\)
attempt to substitute into correct formula for \({\text{P}}(A \cup B)\) (M1)
eg \({\text{P}}(A \cup B) = 0.2 + {\text{P}}(B) – {\text{P}}(A \cap B),{\text{ P}}(A \cup B) = 0.2 + x – 0.2x\)
correct working (A1)
eg \(0.5 = 0.2 + {\text{P}}(B) – 0.2{\text{P}}(B),{\text{ }}0.8x = 0.3\)
\({\text{P}}(B) = \frac{3}{8}{\text{ }}( = 0.375,{\text{ exact}})\) A1 N3
[4 marks]
Question
The following table shows a probability distribution for the random variable \(X\), where \({\text{E}}(X) = 1.2\).
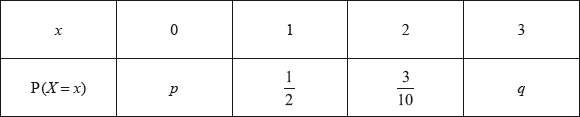
A bag contains white and blue marbles, with at least three of each colour. Three marbles are drawn from the bag, without replacement. The number of blue marbles drawn is given by the random variable \(X\).
A game is played in which three marbles are drawn from the bag of ten marbles, without replacement. A player wins a prize if three white marbles are drawn.
Find \(q\).
Find \(p\).
Write down the probability of drawing three blue marbles.
Explain why the probability of drawing three white marbles is \(\frac{1}{6}\).
The bag contains a total of ten marbles of which \(w\) are white. Find \(w\).
Grant plays the game until he wins two prizes. Find the probability that he wins his second prize on his eighth attempt.
Answer/Explanation
Markscheme
correct substitution into \({\text{E}}(X)\) formula (A1)
eg\(\,\,\,\,\,\)\(0(p) + 1(0.5) + 2(0.3) + 3(q) = 1.2\)
\(q = \frac{1}{{30}}\), 0.0333 A1 N2
[2 marks]
evidence of summing probabilities to 1 (M1)
eg\(\,\,\,\,\,\)\(p + 0.5 + 0.3 + q = 1\)
\(p = \frac{1}{6},{\text{ }}0.167\) A1 N2
[2 marks]
\({\text{P (3 blue)}} = \frac{1}{{30}},{\text{ }}0.0333\) A1 N1
[1 mark]
valid reasoning R1
eg\(\,\,\,\,\,\)\({\text{P (3 white)}} = {\text{P(0 blue)}}\)
\({\text{P(3 white)}} = \frac{1}{6}\) AG N0
[1 mark]
valid method (M1)
eg\(\,\,\,\,\,\)\({\text{P(3 white)}} = \frac{w}{{10}} \times \frac{{w – 1}}{9} \times \frac{{w – 2}}{8},{\text{ }}\frac{{_w{C_3}}}{{_{10}{C_3}}}\)
correct equation A1
eg\(\,\,\,\,\,\)\(\frac{w}{{10}} \times \frac{{w – 1}}{9} \times \frac{{w – 2}}{8} = \frac{1}{6},{\text{ }}\frac{{_w{C_3}}}{{_{10}{C_3}}} = 0.167\)
\(w = 6\) A1 N2
[3 marks]
recognizing one prize in first seven attempts (M1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 7 \\ 1 \end{array}} \right),{\text{ }}{\left( {\frac{1}{6}} \right)^1}{\left( {\frac{5}{6}} \right)^6}\)
correct working (A1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 7 \\ 1 \end{array}} \right){\left( {\frac{1}{6}} \right)^1}{\left( {\frac{5}{6}} \right)^6},{\text{ }}0.390714\)
correct approach (A1)
eg\(\,\,\,\,\,\)\(\left( {\begin{array}{*{20}{c}} 7 \\ 1 \end{array}} \right){\left( {\frac{1}{6}} \right)^1}{\left( {\frac{5}{6}} \right)^6} \times \frac{1}{6}\)
0.065119
0.0651 A1 N2
[4 marks]
Question
The following table shows a probability distribution for the random variable \(X\), where \({\text{E}}(X) = 1.2\).

A bag contains white and blue marbles, with at least three of each colour. Three marbles are drawn from the bag, without replacement. The number of blue marbles drawn is given by the random variable \(X\).
A game is played in which three marbles are drawn from the bag of ten marbles, without replacement. A player wins a prize if three white marbles are drawn.
Jill plays the game nine times. Find the probability that she wins exactly two prizes.
Answer/Explanation
Markscheme
valid approach (M1)
eg\(\,\,\,\,\,\)\({\text{B}}(n,{\text{ }}p),{\text{ }}\left( {\begin{array}{*{20}{c}} n \\ r \end{array}} \right){p^r}{q^{n – r}},{\text{ }}{(0.167)^2}{(0.833)^7},{\text{ }}\left( {\begin{array}{*{20}{c}} 9 \\ 2 \end{array}} \right)\)
0.279081
0.279 A1 N2
[2 marks]
Question
The weights, in grams, of oranges grown in an orchard, are normally distributed with a mean of 297 g. It is known that 79 % of the oranges weigh more than 289 g and 9.5 % of the oranges weigh more than 310 g.
The weights of the oranges have a standard deviation of σ.
The grocer at a local grocery store will buy the oranges whose weights exceed the 35th percentile.
The orchard packs oranges in boxes of 36.
Find the probability that an orange weighs between 289 g and 310 g.
Find the standardized value for 289 g.
Hence, find the value of σ.
To the nearest gram, find the minimum weight of an orange that the grocer will buy.
Find the probability that the grocer buys more than half the oranges in a box selected at random.
The grocer selects two boxes at random.
Find the probability that the grocer buys more than half the oranges in each box.
Answer/Explanation
Markscheme
correct approach indicating subtraction (A1)
eg 0.79 − 0.095, appropriate shading in diagram
P(289 < w < 310) = 0.695 (exact), 69.5 % A1 N2
[2 marks]
METHOD 1
valid approach (M1)
eg 1 − p, 21
−0.806421
z = −0.806 A1 N2
METHOD 2
(i) & (ii)
correct expression for z (seen anywhere) (A1)
eg \(\frac{{289 – u}}{\sigma }\)
valid approach (M1)
eg 1 − p, 21
−0.806421
z = −0.806 (seen anywhere) A1 N2
[2 marks]
METHOD 1
attempt to standardize (M1)
eg \(\sigma = \frac{{289 – 297}}{z},\,\,\frac{{289 – 297}}{\sigma }\)
correct substitution with their z (do not accept a probability) A1
eg \( – 0.806 = \frac{{289 – 297}}{\sigma },\,\,\frac{{289 – 297}}{{ – 0.806}}\)
9.92037
σ = 9.92 A1 N2
METHOD 2
(i) & (ii)
correct expression for z (seen anywhere) (A1)
eg \(\frac{{289 – u}}{\sigma }\)
valid approach (M1)
eg 1 − p, 21
−0.806421
z = −0.806 (seen anywhere) A1 N2
valid attempt to set up an equation with their z (do not accept a probability) (M1)
eg \( – 0.806 = \frac{{289 – 297}}{\sigma },\,\,\frac{{289 – 297}}{{ – 0.806}}\)
9.92037
σ = 9.92 A1 N2
[3 marks]
valid approach (M1)
eg P(W < w) = 0.35, −0.338520 (accept 0.385320), diagram showing values in a standard normal distribution
correct score at the 35th percentile (A1)
eg 293.177
294 (g) A1 N2
Note: If working shown, award (M1)(A1)A0 for 293.
If no working shown, award N1 for 293.177, N1 for 293.
Exception to the FT rule: If the score is incorrect, and working shown, award A1FT for correctly finding their minimum weight (by rounding up)
[3 marks]
evidence of recognizing binomial (seen anywhere) (M1)
eg \(X \sim {\text{B}}\left( {36,\,\,p} \right),\,\,{}_n{C_a} \times {p^a} \times {q^{n – a}}\)
correct probability (seen anywhere) (A1)
eg 0.65
EITHER
finding P(X ≤ 18) from GDC (A1)
eg 0.045720
evidence of using complement (M1)
eg 1−P(X ≤ 18)
0.954279
P(X > 18) = 0.954 A1 N2
OR
recognizing P(X > 18) = P(X ≥ 19) (M1)
summing terms from 19 to 36 (A1)
eg P(X = 19) + P(X = 20) + … + P(X = 36)
0.954279
P(X > 18) = 0.954 A1 N2
[5 marks]
correct calculation (A1)
\({0.954^2},\,\,\left( \begin{gathered}
2 \hfill \\
2 \hfill \\
\end{gathered} \right){0.954^2}{\left( {1 – 0.954} \right)^0}\)
0.910650
0.911 A1 N2
[2 marks]

