Download IITian Academy App for accessing Online Mock Tests and More..
Question
The following diagram shows the graph of \(f(x) = {{\rm{e}}^{ – {x^2}}}\) .
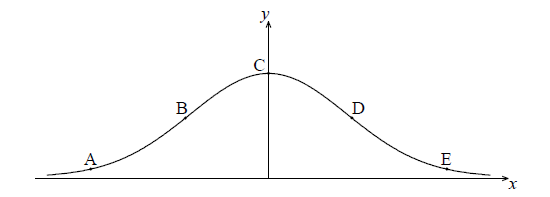
The points A, B, C, D and E lie on the graph of f . Two of these are points of inflexion.
Identify the two points of inflexion.
(i) Find \(f'(x)\) .
(ii) Show that \(f”(x) = (4{x^2} – 2){{\rm{e}}^{ – {x^2}}}\) .
Find the x-coordinate of each point of inflexion.
Use the second derivative to show that one of these points is a point of inflexion.
Answer/Explanation
Markscheme
B, D A1A1 N2
[2 marks]
(i) \(f'(x) = – 2x{{\rm{e}}^{ – {x^2}}}\) A1A1 N2
Note: Award A1 for \({{\rm{e}}^{ – {x^2}}}\) and A1 for \( – 2x\) .
(ii) finding the derivative of \( – 2x\) , i.e. \( – 2\) (A1)
evidence of choosing the product rule (M1)
e.g. \( – 2{{\rm{e}}^{ – {x^2}}}\) \( – 2x \times – 2x{{\rm{e}}^{ – {x^2}}}\)
\( – 2{{\rm{e}}^{ – {x^2}}} + 4{x^2}{{\rm{e}}^{ – {x^2}}}\) A1
\(f”(x) = (4{x^2} – 2){{\rm{e}}^{ – {x^2}}}\) AG N0
[5 marks]
valid reasoning R1
e.g. \(f”(x) = 0\)
attempting to solve the equation (M1)
e.g. \((4{x^2} – 2) = 0\) , sketch of \(f”(x)\)
\(p = 0.707\) \(\left( { = \frac{1}{{\sqrt 2 }}} \right)\) , \(q = – 0.707\) \(\left( { = – \frac{1}{{\sqrt 2 }}} \right)\) A1A1 N3
[4 marks]
evidence of using second derivative to test values on either side of POI M1
e.g. finding values, reference to graph of \(f”\) , sign table
correct working A1A1
e.g. finding any two correct values either side of POI,
checking sign of \(f”\) on either side of POI
reference to sign change of \(f”(x)\) R1 N0
[4 marks]