Question
A discrete random variable X has a probability distribution given by
x | 0 | 1 | 2 |
P(X = x) | p | 3p | 1 − 4p |
where 0 < p < \(\frac{1}{4}\) .
Find an expression for E(X) , in terms of p . [2]
Show that Var(X) = p(7 – 25p). [3]
Christine and Sarah want to estimate the value of p . They take a random sample of n observations of X .
Christine calculates the sample mean, \(\bar{X}\) , and proposes C = \(\frac{2-\bar{X}}{5}\) as an estimator for p .
Show that C is an unbiased estimator for p .
Find Var(C) . [5]
Sarah counts the number of zeros, Y , in the sample of size n. She proposes S = \(\frac{y}{n}\) an estimator for p .
Write down the distribution for Y .
Show that S is an unbiased estimator for p .
Show that Var (s) \(\frac{p(1-p)}{n}\) . [5]
(i) Sketch a graph of the ratio\(\frac{Var(C)}{Var(S}\) the y-axis. for 0 < p < 1 \(\frac{1}{4}\), indicating clearly the scale on
(ii) Hence determine, with a reason, which of C or S is the more efficient estimator. [4]
▶️Answer/Explanation
Ans:
(a)\( E(X)=3P+2(1-4P)(=2-5P)\)
(b)
E\((X^{2})= 3p+4(1-4p)\)
\(Var(X)= 3P+4(1-4P)-(2-5P)^{2}\)
\(=3P+4-16P-4+20P-25P^{2}\)
\(= 7P-25P^{2}\)
\(= P(7-25P)\)
(C)
(i)
E(C)=\(\frac{1}{5}E(2-\bar{X})\)
\(=\frac{1}{5}(2-(2-5P))\)
=P
(ii)
Var(c)= \(\frac{1}{25}Var(2-\bar{X})\)
\(= \frac{1}{25}Var(\bar{X})\)
\(= \frac{P(7-25P)}{25n}\)
(d)
(i) \(Y\sim B(n,p)\)
(ii)
\(E(S)= \frac{1}{n}e(Y)\)
\(= \frac{np}{n}\)
\(= p\)
(iii)
\(Var (S)=\frac{1}{n^{2}}Var(Y)\)
\(= \frac{1}{n^{2}}np(1-p)\)
\(= \frac{p(1-p)}{n}\)
(e)
(i)
\(\frac{Var(C)}{Var(S)}= \frac{P(7-25P)}{25n}.\frac{n}{p(1-p)}=\frac{7-25p}{25(1-p)}\)
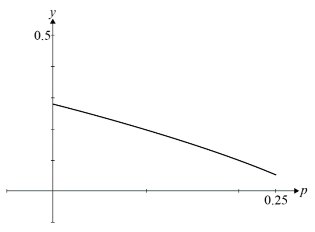
decreasing curve over correct domain with at least 0.25 marked on the
p axis and some number marked on the y axis showing that the
y intercept is significantly less than 1
(ii)
(from the sketch we can see that) \(\frac{Var(C)}{Var(S)}\)<1
so C is a more efficient estimator (as it has lower variance)
Question
(a) A random variable, X , has probability density function defined by
\[f(x) = \left\{ {\begin{array}{*{20}{l}}
{100,}&{{\text{for }} – 0.005 \leqslant x < 0.005} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
Determine E(X) and Var(X) .
(b) When a real number is rounded to two decimal places, an error is made.
Show that this error can be modelled by the random variable X .
(c) A list contains 20 real numbers, each of which has been given to two decimal places. The numbers are then added together.
(i) Write down bounds for the resulting error in this sum.
(ii) Using the central limit theorem, estimate to two decimal places the probability that the absolute value of the error exceeds 0.01.
(iii) State clearly any assumptions you have made in your calculation.
▶️Answer/Explanation
Markscheme
(a) f(x)is even (symmetrical about the origin) (M1)
\({\text{E}}(X) = 0\) A1
\({\text{Var}}(X) = {\text{E}}({X^2}) = \int_{ – 0.005}^{0.005} {100{x^2}{\text{d}}x} \) (M1)(A1)
\( = 8.33 \times {10^{ – 6}}\left( {{\text{accept }}0.83 \times {{10}^{ – 5}}{\text{ or }}\frac{1}{{120\,000}}} \right)\) A1
[5 marks]
(b) rounding errors to 2 decimal places are uniformly distributed R1
and lie within the interval \( – 0.005 \leqslant x < 0.005.\) R1
this defines X AG
[2 marks]
(c) (i) using the symbol y to denote the error in the sum of 20 real numbers each rounded to 2 decimal places
\( – 0.1 \leqslant y( = 20 \times x) < 0.1\) A1
(ii) \(Y \approx {\text{N}}(20 \times 0,{\text{ }}20 \times 8.3 \times {10^{ – 6}}) = {\text{N}}(0,{\text{ }}0.00016)\) (M1)(A1)
\({\text{P}}\left( {\left| Y \right| > 0.01} \right) = 2\left( {1 – {\text{P}}(Y < 0.01)} \right)\) (M1)(A1)
\( = 2\left( {1 – {\text{P}}\left( {Z < \frac{{0.01}}{{0.0129}}} \right)} \right)\)
\( = 0.44\) to 2 decimal places A1 N4
(iii) it is assumed that the errors in rounding the 20 numbers are independent R1
and, by the central limit theorem, the sum of the errors can be modelled approximately by a normal distribution R1
[8 marks]
Total [15 marks]
Question
The continuous random variable X has probability density function f given by
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{\frac{{3{x^2} + 2x}}{{10}},}&{{\text{for }}1 \leqslant x \leqslant 2} \\
{0,}&{{\text{otherwise}}{\text{.}}}
\end{array}} \right.\]
a.(i) Determine an expression for \(F(x)\), valid for \(1 \leqslant x \leqslant 2\), where F denotes the cumulative distribution function of X.
(ii) Hence, or otherwise, determine the median of X.[6]
b.(i) State the central limit theorem.
(ii) A random sample of 150 observations is taken from the distribution of X and \(\bar X\) denotes the sample mean. Use the central limit theorem to find, approximately, the probability that \(\bar X\) is greater than 1.6.[8]
▶️Answer/Explanation
Markscheme
(i) \(F(x) = \int_1^x {\frac{{3{u^2} + 2u}}{{10}}{\text{d}}u} \) (M1)
\( = \left[ {\frac{{{u^3} + {u^2}}}{{10}}} \right]_1^x\) A1
Note: Do not penalise missing or wrong limits at this stage.
Accept the use of x in the integrand.
\( = \frac{{{x^3} + {x^2} – 2}}{{10}}\) A1
(ii) the median m satisfies the equation \(F(m) = \frac{1}{2}\) so (M1)
\({m^3} + {m^2} – 7 = 0\) (A1)
Note: Do not FT from an incorrect \(F(x)\).
\(m = 1.63\) A1
Note: Accept any answer that rounds to 1.6.
[6 marks]
(i) the mean of a large sample from any distribution is approximately
normal A1
Note: This is the minimum acceptable explanation.
(ii) we require the mean \(\mu \) and variance \({\sigma ^2}\) of X
\(\mu = \int_1^2 {\left( {\frac{{3{x^3} + 2{x^2}}}{{10}}} \right){\text{d}}x} \) (M1)
\( = \frac{{191}}{{120}}{\text{ }}(1.591666 \ldots )\) A1
\({\sigma ^2} = \int_1^2 {\left( {\frac{{3{x^4} + 2{x^3}}}{{10}}} \right){\text{d}}x – {\mu ^2}} \) (M1)
\( = 0.07659722 \ldots \) A1
the central limit theorem states that
\(\bar X \approx N\left( {\mu ,\frac{{{\sigma ^2}}}{n}} \right),\) i.e. \(N(1.591666 \ldots ,{\text{ }}0.0005106481 \ldots )\) M1A1
\({\text{P}}(\bar X > 1.6) = 0.356\) A1
Note: Accept any answer that rounds to 0.36.
[8 marks]
Question
John rings a church bell 120 times. The time interval, \({T_i}\), between two successive rings is a random variable with mean of 2 seconds and variance of \(\frac{1}{9}{\text{ second}}{{\text{s}}^2}\).
Each time interval, \({T_i}\), is independent of the other time intervals. Let \(X = \sum\limits_{i = 1}^{119} {{T_i}} \) be the total time between the first ring and the last ring.
The church vicar subsequently becomes suspicious that John has stopped coming to ring the bell and that he is letting his friend Ray do it. When Ray rings the bell the time interval, \({T_i}\) has a mean of 2 seconds and variance of \(\frac{1}{{25}}{\text{ second}}{{\text{s}}^2}\).
The church vicar makes the following hypotheses:
\({H_0}\): Ray is ringing the bell; \({H_1}\): John is ringing the bell.
He records four values of \(X\). He decides on the following decision rule:
If \(236 \leqslant X \leqslant 240\) for all four values of \(X\) he accepts \({H_0}\), otherwise he accepts \({H_1}\).
a.Find
(i) \({\text{E}}(X)\);
(ii) \({\text{Var}}(X)\).[3]
b.Explain why a normal distribution can be used to give an approximate model for \(X\).[2]
c.Use this model to find the values of \(A\) and \(B\) such that \({\text{P}}(A < X < B) = 0.9\), where \(A\) and \(B\) are symmetrical about the mean of \(X\).[7]
d.Calculate the probability that he makes a Type II error.[5]
▶️Answer/Explanation
Markscheme
(i) \({\text{mean}} = 119 \times 2 = 238\) A1
(ii) \({\text{variance}} = 119 \times \frac{1}{9} = \frac{{119}}{9}{\text{ }}( = 13.2)\) (M1)A1
Note: If 120 is used instead of 119 award A0(M1)A0 for part (a) and apply follow through for parts (b)-(d). (b) is unaffected and in (c) the interval becomes \((234,{\text{ }}246)\). In (d) the first 2 A1 marks are for \(0.3633 \ldots \) and \(0.0174 \ldots \) so the final answer will round to 0.017.
[3 marks]
justified by the Central Limit Theorem R1
since \(n\) is large A1
Note: Accept \(n > 30\).
[2 marks]
\(X \sim N\left( {238,{\text{ }}\frac{{119}}{9}} \right)\)
\(Z = \frac{{X – 238}}{{\frac{{\sqrt {119} }}{3}}} \sim N(0,{\text{ }}1)\) (M1)(A1)
\({\text{P}}(Z < q) = 0.95 \Rightarrow q = 1.644 \ldots \) (A1)
so \({\text{P}}( – 1.644 \ldots < Z < 1.644 \ldots ) = 0.9\) (R1)
\({\text{P}}( – 1.644 \ldots < \frac{{X – 238}}{{\frac{{\sqrt {119} }}{3}}} < 1.644 \ldots ) = 0.9\) (M1)
interval is \(232 < X < 244{\text{ }}({\text{3sf}}){\text{ }}(A = 232,{\text{ }}B = 244)\) A1A1
Notes: Accept the use of inverse normal applied to the distribution of \(X\).
Alternative is to use the GDC to find a pretend \(Z\) confidence interval for a mean and then convert by multiplying by 119.
Either \(A\) or \(B\) correct implies the five implied marks.
Accept any numbers that round to these 3sf numbers.
[7 marks]
under \({{\text{H}}_1},{\text{ }}X \sim N\left( {238,{\text{ }}\frac{{119}}{9}} \right)\) (M1)
\({\text{P}}(236 \leqslant X \leqslant 240) = 0.41769 \ldots \) (A1)
probability that all 4 values of \(X\) lie in this interval is
\({(0.41769 \ldots )^4} = 0.030439 \ldots \) (M1)(A1)
so probability of a Type II error is 0.0304 (3sf) A1
Note: Accept any answer that rounds to 0.030.
[5 marks]
