This question is about forces.
A stone block is pulled at constant speed up an incline by a cable attached to an electric motor.
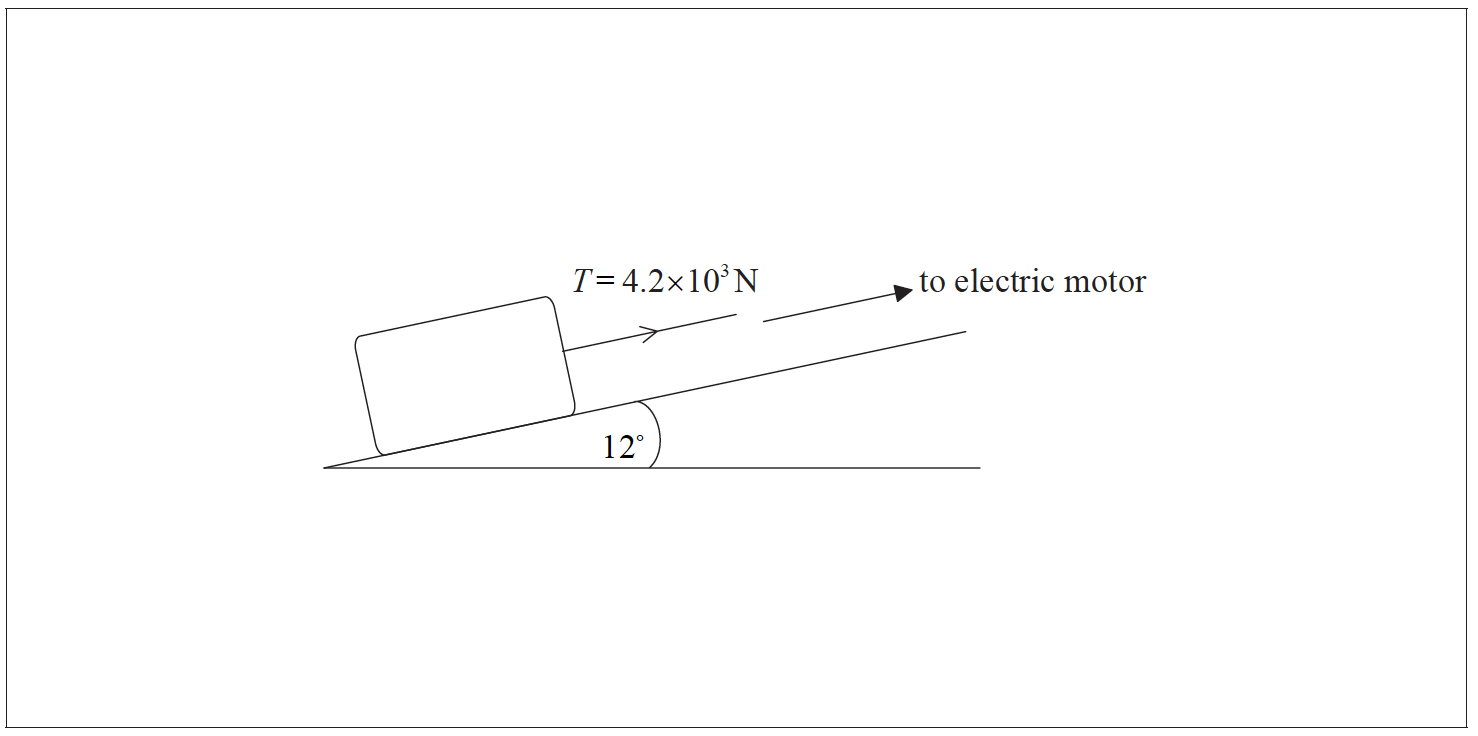
The incline makes an angle of 12 ° with the horizontal. The weight of the block is 1.5×104N and the tension T in the cable is 4.2×103N.
a. On the diagram draw and label arrows that represent the forces acting on the block. [2]
Answer/Explanation
Markscheme
a.
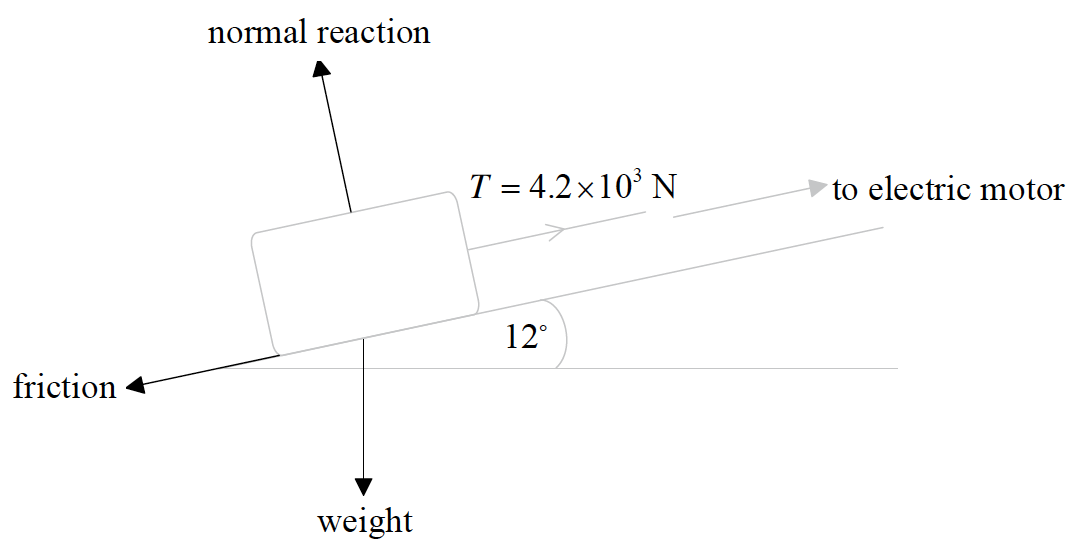
(normal) reaction/N/R and weight/force of gravity/gravity force/gravitational force/mg/w/W with correct directions;
friction/frictional force/F/Ff with arrow pointing down ramp along surface of ramp;
Do not allow “gravity” as label. Do not allow “drag” as label for friction.
W sin θ=3.1×103N;
friction=1.1×103N;
This question is in two parts. Part 1 is about Newton’s laws and momentum. Part 2 is about the greenhouse effect.
Part 1 Newton’s laws and momentum
Part 2 The greenhouse effect
a. State the condition for the momentum of a system to be conserved. [1]
(i) Outline how Newton’s third law and the conservation of momentum apply as the ball is thrown.
(ii) Explain, with reference to Newton’s second law, why the horizontal momentum of the ball remains constant whilst the ball is in flight. [5]
Mass of truck X=3.7×103 kg
Mass of truck Y=6.3×103 kg
Speed of X just before collision=4.0 m s–1
(i) Calculate v.
(ii) Determine the kinetic energy lost as a result of the collision. [4]
(i) Identify two greenhouse gases.
(ii) Discuss, with reference to the mechanism of infrared absorption, why the temperature of the Earth’s surface would be lower if there were no greenhouse gases present in the atmosphere. [5]
Answer/Explanation
Markscheme
a. the net (external) force acting on the system is zero / no force acting on system / system is isolated;
force on ball must be equal and opposite to force on the person;
so ball and person/Earth/pond move in opposite directions;
(ii) Newton’s second law states that the rate of change of momentum is equal/proportional/directly proportional to the force acting;
the horizontal force acting on the ball is zero therefore the momentum must be constant/the rate of change of momentum is zero;
or
Newton’s second law can be expressed as the force acting is equal to the product of mass and acceleration;
the horizontal force acting on the ball is zero therefore the acceleration is zero so velocity is constant (and therefore momentum is constant);
\(F = \frac{P}{v}\) or \(\frac{{0.75 \times {{10}^6}}}{{44}}\);
17kN;
v=1.5ms−1;
(ii) KE lost\( = \frac{1}{2}\left[ {3.7 \times {{10}^3} \times {{4.0}^2}} \right] – \frac{1}{2}\left[ {10 \times {{10}^3} \times {{1.5}^2}} \right]\);
=18kJ;
friction\( = \frac{{11250}}{{40}}\);
=280 N;
or
use of kinematic equation to give a=0.274ms–1;
use of F(=ma)=10×103a;
270/280 N;
(i) methane/CH4, water vapour/H2O, carbon dioxide/CO2, nitrous oxide/N2O;
Award [1] for any two of the above.
(ii) mechanism:
mention of resonance;
natural frequency of (resonating) greenhouse gas molecules is same as that of infrared radiation from Earth;
or
mention of energy level differences;
differences between energy levels of greenhouse gas molecules matches energy of infrared radiation from Earth;
explanation:
less infrared trapped if absorption is reduced;
so more infrared is transmitted through atmosphere;
or
more infrared is trapped if absorption is increased;
so more infrared is re-radiated back to Earth;
Allow only one variant for each alternative.
leading to an increase in temperature of glaciers/surface;
less glacier area so less reflection from glacier surface / OWTTE;
albedo defined as \(\frac{{{\rm{amount of radiation reflected}}}}{{{\rm{amount of radiation absorbed}}}}\) therefore albedo reduced;
This question is about circular motion.
A ball of mass 0.25 kg is attached to a string and is made to rotate with constant speed v along a horizontal circle of radius r = 0.33m. The string is attached to the ceiling and makes an angle of 30 ° with the vertical.
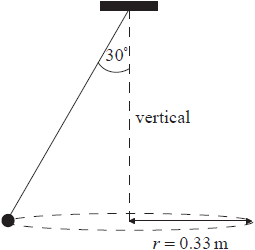
a (i) On the diagram above, draw and label arrows to represent the forces on the ball in the position shown.
(ii) State and explain whether the ball is in equilibrium. [4]
Determine the speed of rotation of the ball. [3]
Answer/Explanation
Markscheme
a. (i) [1] each for correct arrow and (any reasonable) labelling;
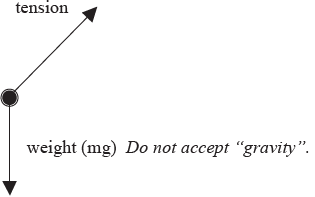
Award [1 max] for arrows in correct direction but not starting at the ball.
(ii) no;
because the two forces on the ball can never cancel out / there is a net force on
the ball / the ball moves in a circle / the ball has acceleration/it is changing
direction;
Award [0] for correct answer with no or wrong argument.
\(T\left( { = \frac{{mg}}{{\cos {{30}^ \circ }}}} \right) = 2.832{\rm{N}}\);
\(\frac{{m{v^2}}}{r} = T\sin {30^ \circ }\);
\(v = \left( {\sqrt {\frac{{Tr\sin {{30}^ \circ }}}{m}} = \sqrt {\frac{{2.832 \times 0.33 \times \sin {{30}^ \circ }}}{{0.25}}} } \right) = 1.4{\rm{m}}{{\rm{s}}^{ – 1}}\);
or
\(T\cos {30^ \circ } = mg\);
\(T\sin {30^ \circ } = \frac{{m{v^2}}}{r}\);
\(v = \left( {\sqrt {gr\tan {{30}^ \circ }} = \sqrt {9.81 \times 0.33 \times \tan {{30}^ \circ }} } \right) = 1.4{\rm{m}}{{\rm{s}}^{ – 1}}\);
