IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 2.3 – Work , Energy and Power
Topic 2 Weightage : 13 %
All Questions for Topic 2.3 – Kinetic energy , Gravitational potential energy , Elastic potential energy ,Work done as energy transfer , Power as rate of energy transfer , Principle of conservation of energy , Efficiency
Question
An electron has a linear momentum of 4.0 × 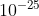 kg m
kg m 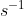 . What is the order of magnitude of the kinetic energy of the electron?
. What is the order of magnitude of the kinetic energy of the electron?
A. 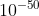 J
J
B. 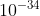 J
J
C. 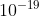 J
J
D. 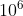 J
J
▶️Answer/Explanation
Ans: C
Ref : https://www.iitianacademy.com/ib-physics-topic-2-mechanics-2-4-momentum-and-impulse-study-notes/
KINETIC ENERGY
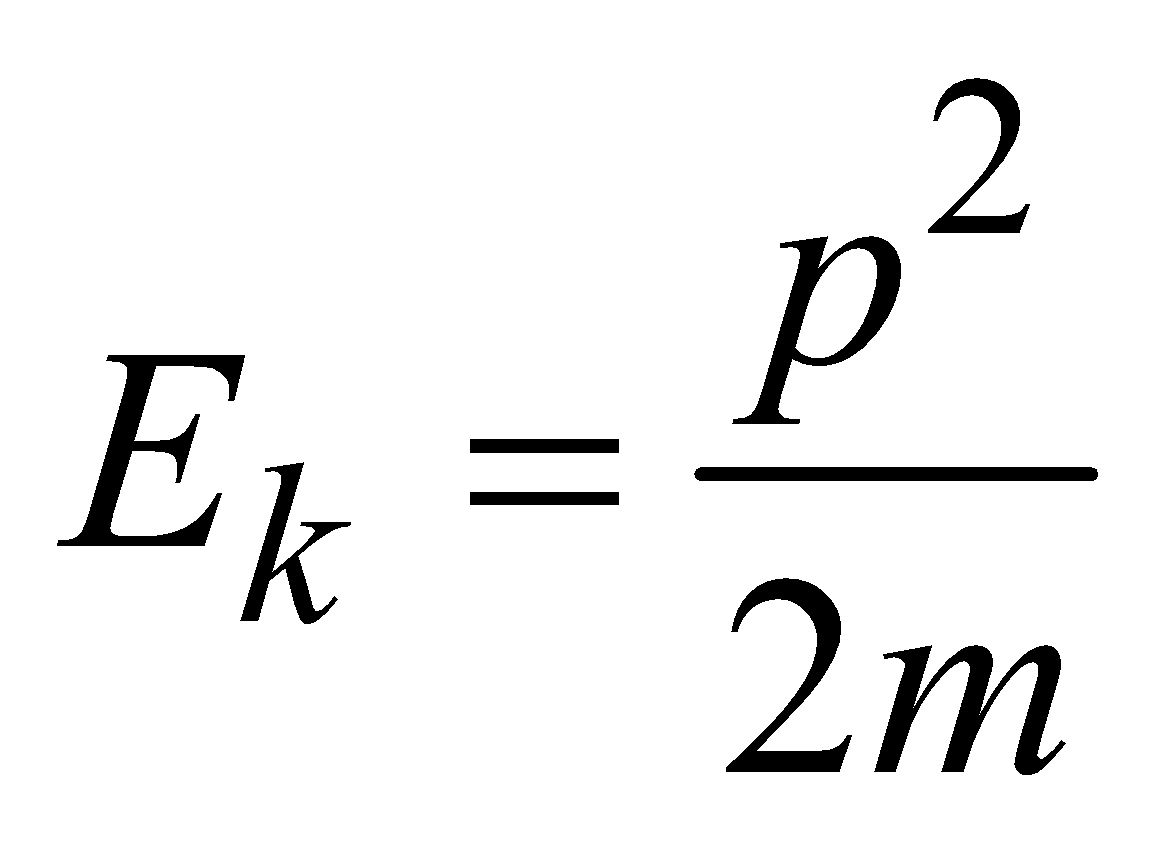 …(iii)
…(iii)Question
A car takes 20 minutes to climb a hill at constant speed. The mass of the car is 1200 kg and the car gains gravitational potential energy at a rate of 6.0 kW. Take the acceleration of gravity to be 10 m 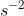 . What is the height of the hill?
. What is the height of the hill?
A 0.6 m
B 10 m
C 600 m
D 6000 m
▶️Answer/Explanation
Ans: C
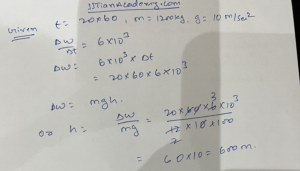
Question
A heat engine does 300 J of work during one cycle. In this cycle 900 J of energy is wasted. What is the efficiency of the engine?
A. 0.25
B. 0.33
C. 0.50
D. 0.75
▶️Answer/Explanation
Markscheme
A
Heat Engine :
A Heat engine is a device which helps us to get an amount of work when connected to two thermal reservoirs, one at a higher temperature and another one at a lower temperature.
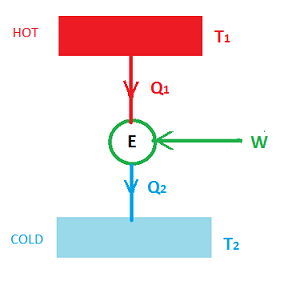
In the above diagram, we can see
- Two thermal reservoirs one at a higher temperature \(T_1 \) and at a lower temperature \(T_2 \)
- Heat \(Q_1 \) flows from the higher temperature reservoir to the engine E
- \(W \) is the work obtained in the Engine
- Heat \(Q_2 \) flows from the engine to the cold reservoir.
- \(Q_1=W+Q_2 \)
The efficiency of a thermal reservoir is given as
\(\eta = \frac {W}{Q_1}=\frac {Q_1-Q_2}{Q_1}= \frac {T_1-T_2}{T_1} \)
Given that a heat engine does W = 300 J of work while exhausting \(Q_2=900 J \).
Heat supplied to the heat engine is given by \(Q_1 =W+Q_2 =300J +900J = 1200J \)
The efficiency of the engine is given by
\(\begin{align*} \eta &= \frac {W}{Q_1}\\ &= \frac {300}{1200}\\ &=0.25 \Rightarrow (Answer) \end{align*} \)
Question
An object of mass \(m\) is initially at rest. When an impulse \(I\) acts on the object its final kinetic energy is \({E_{\text{K}}}\). What is the final kinetic energy when an impulse of \({\text{2}}I\) acts on an object of mass \({\text{2}}m\) initially at rest?
A. \(\frac{{{E_{\text{K}}}}}{2}\)
B. \({E_{^{\text{K}}}}\)
C. \(2{E_{^{\text{K}}}}\)
D. \(4{E_{^{\text{K}}}}\)
▶️Answer/Explanation
Markscheme
C
\(E_k=\frac{1}{2}mv^2\)
\(I= \Delta P= m(v_f-v_i)=mv\)
or\( v=\frac{I}{m}\)
or \(\frac{1}{2}mv^2 =\frac{1}{2}m\frac{I^2}{m^2} =\frac{I^2}{2m}\)
\(E_k=\frac{I^2}{2m}\)
\(E_k’=\frac{(2I)^2}{2(2m)}=2 (\frac{I^2}{2m}) =2E_k\)
Question
An object of mass m1 has a kinetic energy E1. Another object has a mass m2 and kinetic energy E2. The objects have the same momentum. What is the ratio \(\frac{{{E_1}}}{{{E_2}}}\)?
A. 1
B. \(\sqrt {\frac{{{m_2}}}{{{m_1}}}} \)
C. \(\frac{{{m_2}}}{{{m_1}}}\)
D. \({\left( {\frac{{{m_2}}}{{{m_1}}}} \right)^2}\)
▶️Answer/Explanation
Markscheme
C
\(E_k=\frac{1}{2}mv^2 , P =mv\)
hence
\(E_k = \frac{P^2}{2m}\)
\(E_{k1}=\frac{P^2}{2m_1}\)
\(E_{k2}=\frac{P^2}{2m_2}\)
\(\frac{E_{k1}}{E_{k2}} =\frac{\frac{P^2}{2m_1}}{\frac{P^2}{2m_2}}=\frac{m_2}{m_1}\)
Question
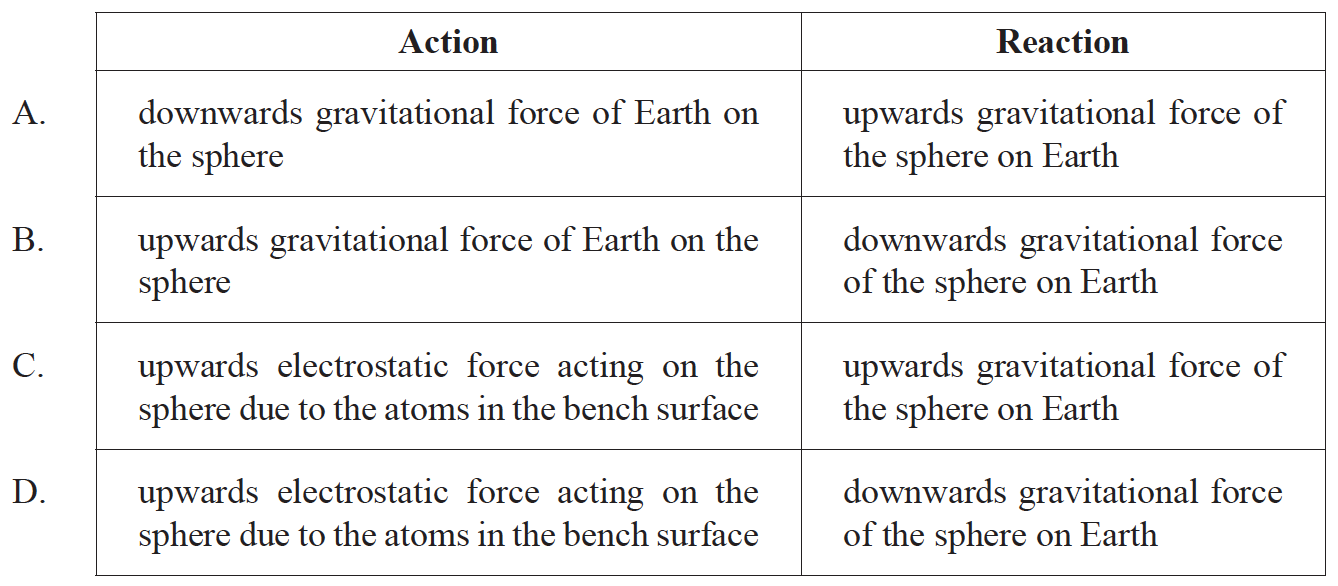
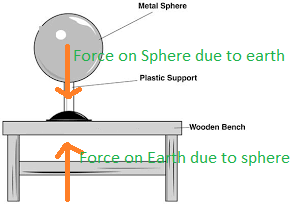
A metal sphere is at rest on a bench. According to Newton’s third law of motion, what is a possible action-reaction pair for this situation?
▶️Answer/Explanation
Markscheme
A
Question
A driving force F acts on a car which moves with constant velocity v. The quantity Fv is equivalent to the
A. useful power developed by the engine of the car.
B. work done by the car against resistive forces.
C. energy of the car.
D. rate of change of momentum of the car.
▶️Answer/Explanation
Markscheme
A
Ref: https://www.iitianacademy.com/ib-physics-unit-2-work-energy-and-power-notes/
Other way
Looking at the units helps here: with force in N and velocity in ms-1 the product will be in Nms-1 or Js-1 that is, W; so the correct response must be power.
Question
A block of mass m is moving at constant velocity v along a frictionless surface that is height h above the ground.
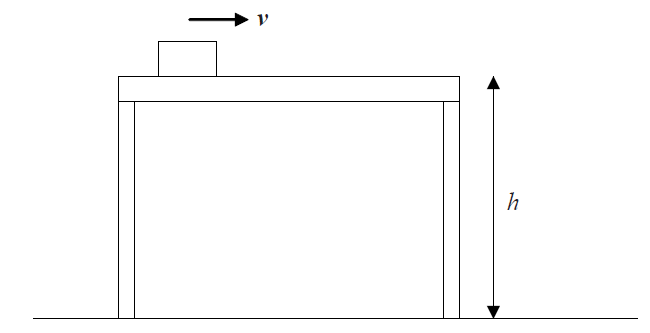
Which expression gives the work necessary to maintain the constant velocity?
A. mgh
B. \(\frac{1}{2}\)mv2
C. mgh+\(\frac{1}{2}\)mv2
D. zero
▶️Answer/Explanation
Markscheme
D
