12.2 Nuclear physics
Essential Idea:
The idea of discreteness that we met in the atomic world continues to exist in the nuclear world as well
Understandings:
- Rutherford scattering and nuclear radius
- Nuclear energy levels
- The neutrino
- The law of radioactive decay and the decay constant
Applications and Skills:
- Describing a scattering experiment including location of minimum intensity for the diffracted particles based on their de Broglie wavelength
- Explaining deviations from Rutherford scattering in high energy experiments
- Describing experimental evidence for nuclear energy levels
- Solving problems involving the radioactive decay law for arbitrary time intervals
- Explaining the methods for measuring short and long half-lives
Data booklet reference:
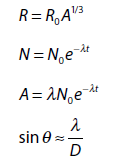
Nuclear Physics
Rutherford Scattering
Simple energy considerations can be used to calculate the distance of closest approach of an alpha-particle.
- If the alpha-particle initially has kinetic energy upon approaching, when it stops close to the nucleus due to the electrostatic repulsion, the electrical potential energy of the alpha particle will , where is the atom’s proton number.
- An alpha-particle approaching with high kinetic energy will get closer to the nuclear (closest = nuclear radius).
- \(\mathbf{R\ = \ }\mathbf{R}_{\mathbf{0}}\mathbf{A}^{\mathbf{1/3}}\) is the radius, is the Fermi radius ( \(1.2 \times 10^{- 15}\text{\ m}\)) and is the mass number.
- All nuclei have the same density, and so their volume is given by
\(\mathbf{V\ = \ 4/3\ \pi}\mathbf{R}^{\mathbf{3}}\mathbf{\ = \ 4/3\ \pi A}{\mathbf{R}_{\mathbf{0}}}^{\mathbf{3}}.\)
- All nuclei have the same density, and so their volume is given by
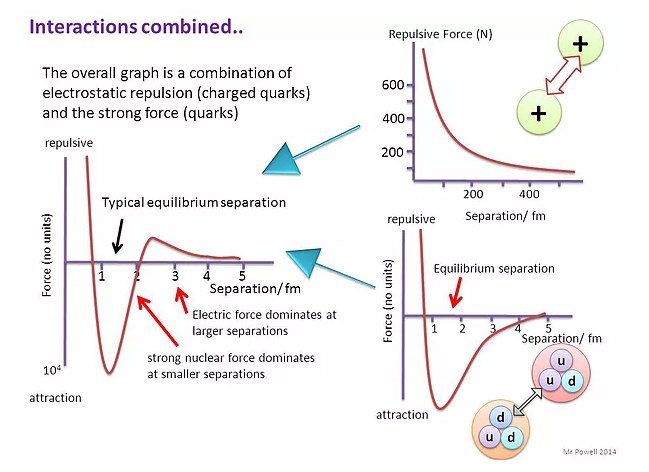
- Derivations from Rutherford scattering: When the alpha-particles have very high kinetic energy, and thus, the distance of closest approach is equal or less than \(10^{- 15}m\), deviations are observed, which is an evidence of the existence of the strong nuclear force, i.e. they are absorbed.
- The derivation of the Rutherford formula is based on a number of assumptions. The most important is that the only force in play during the scattering process is the electric force. As the energy of the alpha particles increases, the alpha particles can get closer to the nucleus. When the distance of closest approach gets to be about 10−15 m or less, deviations from the Rutherford formula are observed . This is due to the fact that the alpha particles are so close to the nucleus that the strong nuclear force begins to act on the alpha particles.
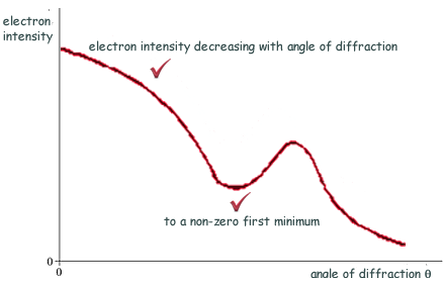
Electron diffraction
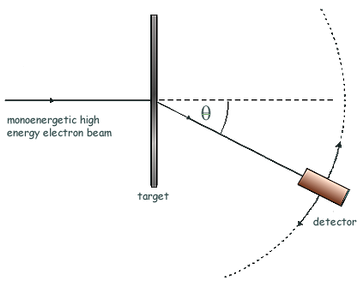
If the de Broglie wavelength ** **of the electrons is about the same as the nuclear diameter , then a minimum will be formed at . **Useful **to measure nuclear radius.
- More accurate than Rutherford scattering, because strong force does not affect electrons.
- When electrons of much higher energy are used, the collisions are no longer elastic and energy is converted into mass, as several mesons are emitted from the nucleus
- At high energies,** **the electrons penetrate into the nucleus and scatter off the quarks within protons and neutrons, something known as deep inelastic scattering, providing evidence for the quark model.
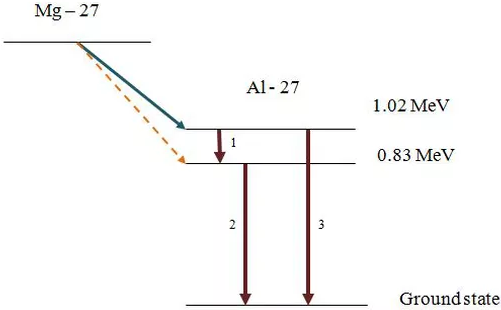
Nuclear energy levels
The emission of alpha and beta particles by radioactive decay often leaves the **daughter nuclei in an excited discrete energy state **(similar to electron energy levels). The state depends on the energy of the alpha or beta particle.
Alpha decay
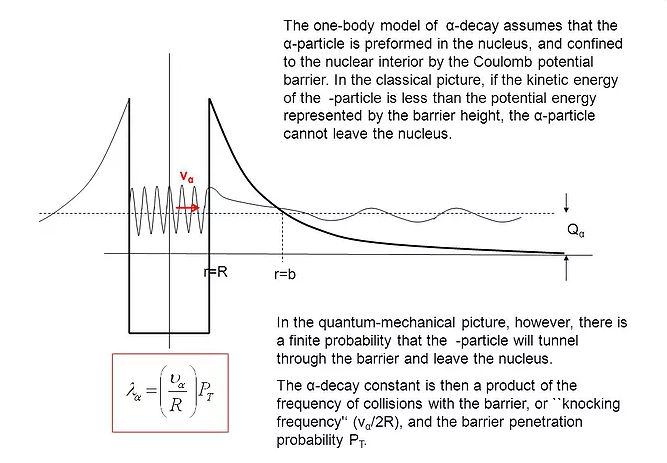
Alpha-particles form as clusters of two protons and two neutros inside the nucleus well before they are emitted as alpha-particles. This is because the nucleons are in random motion within the nucleus but their kinetic energies are much smaller than those needed to escape.
- The wave function │Ψ│ of the alpha-particles is not localized to the nucleus and allows overlaps with the potential energy barrier provided by the strong nuclear force, which means that there is a finite but very small probability of observing the alpha-particles outside the nucleus (thanks to quantum tunneling).
- Higher potential barriers and greater thickness to cross means a longer lifetime (e.g. polonium).
Negative beta decay
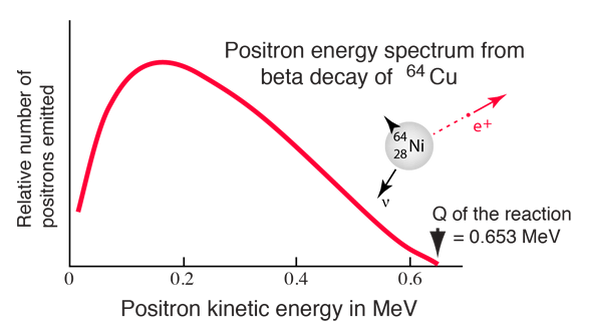
Since the beta particles have a continuous energy spectrum, in order to conserve mass, energy, and momentum, the existence of the neutrino was suggested by Pauli (and later anti-neutrino)
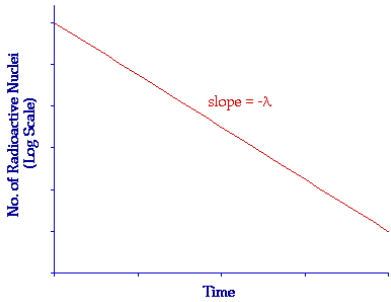
The law of radioactive decay
- Decay constant (): The probability that an individual nucleus will decay in a given time interval (e.g.)
- Units:\(s^{- 1},\ min^{- 1},\ hour^{- 1},\ day^{- 1}\text{…\!}\)
- Relationship with half-life:
- Activity (): Number of nuclei decaying in a second in a sample
- Units: becquerel (Bq)
- In a sample of undecayed nuclei, the activity will be given by .
- Formulas:
\(\mathbf{N\ = \ }\mathbf{N}_{\mathbf{0}}\mathbf{e}^{\mathbf{- \lambda t}}\mathbf{;\ A\ = \ }\mathbf{A}_{\mathbf{0}}\mathbf{e}^{\mathbf{- \lambda t}}\mathbf{;\ A\ = \ \lambda}\mathbf{N}_{\mathbf{0}}\mathbf{e}^{\mathbf{- \lambda t}}\)where \(\mathbf{A}_{\mathbf{0}}\mathbf{\ = \ \lambda}\mathbf{N}_{\mathbf{0}}\) is the initial activity.
- **Measuring long half-lives: **Not possible to measure using a G-M tube. In these cases, a pure sample of the nuclide in a known chemical form needs to be separated, its mass measured and then a count rate taken. From this reading, the activity can be calculated by multiplying the count rate by the ratio
NUCLEI
SOME IMPORTANT FACTS ABOUT ATOMIC MASS, SIZE AND COMPOSITION OF NUCLEUS
- Proton was discovered by Goldstein
- Atomic mass unit
1.a.m.u = 1/12th of mass of C-12 isotope,
1 a.m.u = 1.660565 × 10–27 kg - Mass of a proton, mp = 1.0073 a.m.u = 1.6726 × 10–27 kg
- Chadwick’s experiment
Neutrons were detected.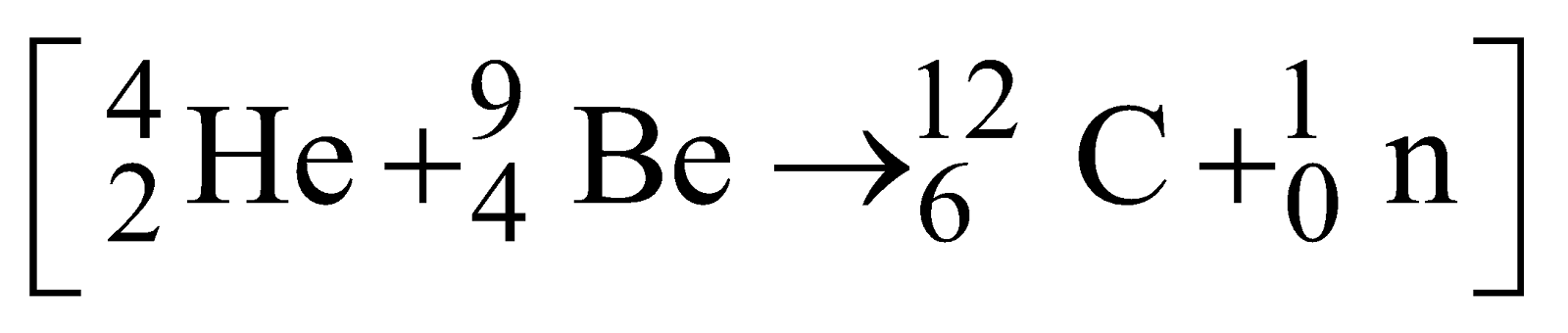 - Mass of neutron, mn = 1.00866 a.m.u = 1.6749 × 10–27 kg
- Mass of electron = 9.1 ×10–31 kg
- Mass number, A = total number of nucleons (neutrons + protons present in the nucleus of an atom)
- Atomic number, Z = number of protons = number of electrons
- Types of nuclei :
- Isotopes : The atoms of the element which have the same atomic number but different atomic mass numbers. e.g., 1H1, 1H2, 1H3 ; 8O16, 8O17, 8O18
- Isobars : The atoms of differents element which have the same atomic mass number but different atomic numbers. e.g., 6C14, 7N14, 18Ar40, 20Ca40 etc.
- Isotones : The nuclides which contain the same number of neutrons e.g., 2H23, 2He24, 2Be59, 5Be510 etc.
- Isomers : having same mass number, same atomic number but different radioactive properties.
- Rest mass of nucleus is less than sum of rest masses of constituent nucleons, the difference is called mass defect.
- Size of the nucleus : Radius of nucleus, R = R0 A1/ 3 where R0 = 1.1 × 10–15 m.
- Nuclear density of all elements ~ 1017 kg m–3.
MASS ENERGY AND NUCLEAR BINDING ENERGY
Einstein’s mass energy equivalence i.e., E = mc2 gives :
and 1MeV = 1.6 × 10–13 J
BINDING ENERGY
Binding energy of a nucleus is the energy with which nucleons are bound in the nucleus. It is measured by the work required to be done to separate the nucleons an infinite distance apart from the nucleus, so that they may not interact with one another.
Total 
mp = mass of proton; mn = mass of neutron
mN = mass of nucleons (protons + neutrons)
Z = Atomic number
A = atomic mass
Binding Energy per Nucleon
The binding energy per nucleon of a nucleus is the average energy required to extract a nucleon from the nucleus.
Binding energy per nucleon
The graph of binding energy per nucleon with mass number A is as shown below.
Binding energy per nucleon gives a measure of stability of nucleus. More is binding energy per nucleon more is the stability of nucleus. Binding energy per nucleon is small for lighter nuclei
i.e. 1H1, 1H2 etc.
For A < 28 at A = 4n the curve shows some peaks at 2He4, 4Be8, 6C16, 8O16, 10Ne20, 12Mg24 .
This represents extra stability of these elements with respect to their neighbours.
KEEP IN MEMORY
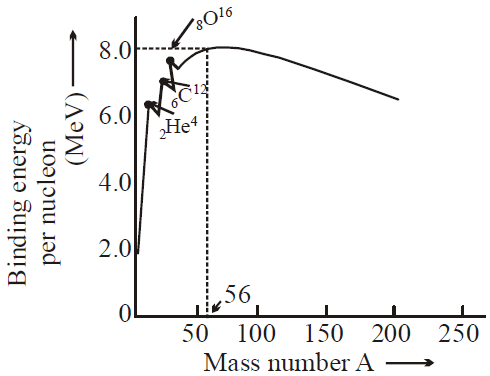
- A nuclide is a specific nucleus of an atom characterised as ZXA where A = mass number and Z = atomic number.
- Binding energy per nucleon is nearly 8.4 MeV for nuclei in the range of mass number 40 to 120.
- Binding energy is highest in Fe56.( 8.8 MeV)
- Binding energy curve predicts :
- Fission : Breaking up of a heavy nucleus (A > 200) into two nuclei of approximately equal size, and release of energy.
- Fusion : Lighter nuclei ( A < 20) combine together to form heavier nucleus and release of energy.
- BE/ A varies by less than 10% above A = 10 suggests that each nucleon interacts with its neighbouring nucleon only.
- For A > 56, BE/A decreases because of the destabilising effect of long-range coulombic force.
NUCLEAR FORCE
It is the force acts in the nucleus between the nucleons and is responsible for binding the nucleon.
CHARACTERISTICS OF NUCLEAR FORCE
- It is a short range force effective only in range 10–15 m
- It is charge independent. It acts between proton-proton, proton-neutron and neutron – neutron.
- It is not a central force.
- It is spin dependent.
- It is 1038 times stronger than gravitational force and 102 times stronger than electric force.
- The main cause of nuclear force is the exchange of π− mesons between nucleus
, 
, 
RADIOACTIVITY
It is the spontaneous disintegration of the heavy nucleus of an atom. It occurs without external provocation.
There are three main types of radioactive radiations.
- α-rays (i.e., Helium nuclei or α – particles)
- β-rays (i.e., electron or positron or β – particles)
- γ-rays (photons or gamma radiations)
It is a process by which an unstable nuclei achieves stability. This process is not affected by
- chemical combination
- changing physical environment other than nuclear bombardment
FEATURES OF RADIOACTIVITY
- It is a statistical process.
- When a nucleus undergoes alpha or beta decay, its atomic number and mass number changes (in β-decay only atomic number changes) & it transforms into a new element.
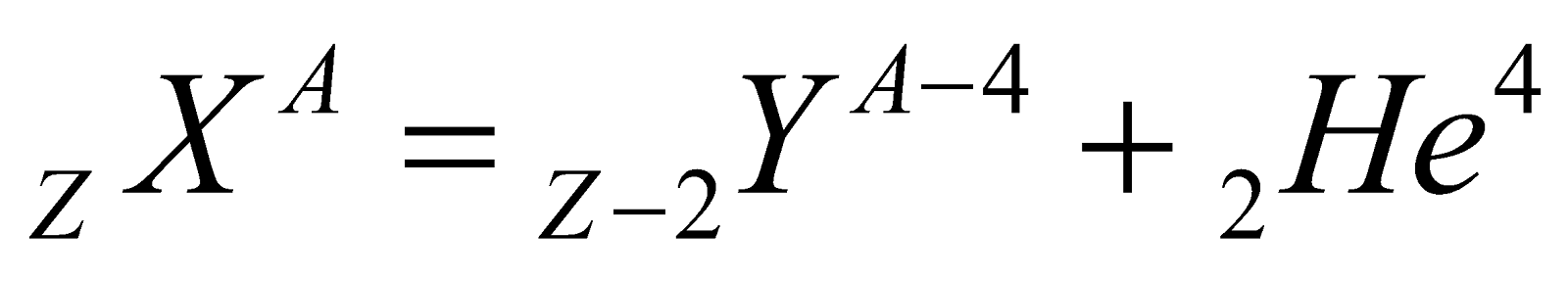(α-particle), it means that by emission of alpha particle (α-particle), it loses 2 units of charge and 4 units of mass.
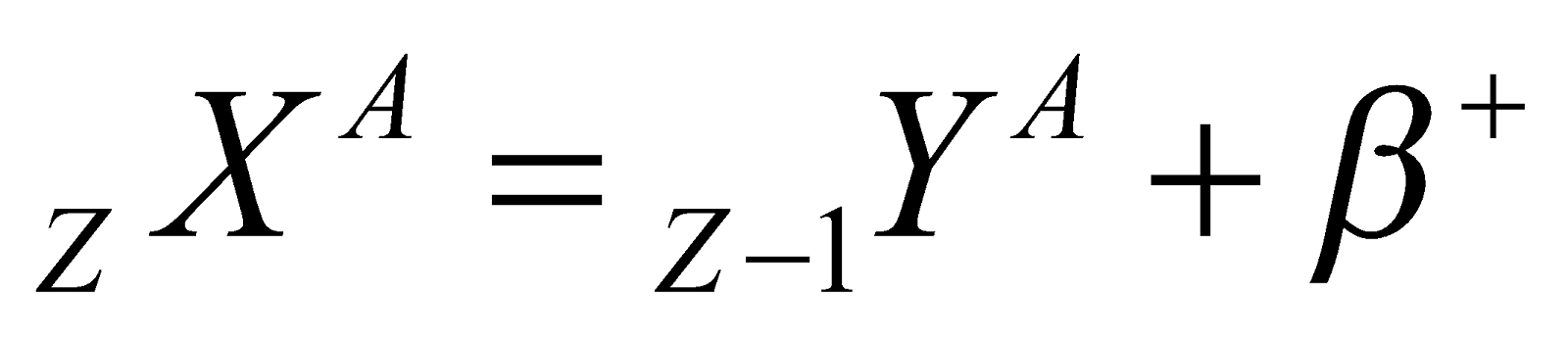(positron). It means that by emission of beta particle (β+-particle), nucleus loses one unit of charge. It is surprising to note that a nucleus does not contain β+ then how is it emitted. Reason : During a β+ particle(i.e., positron) decay, a protron converts into a neutron
(neutrino).A β– particle (i.e., electron) decays, when inside the nucleus a neutron converts into a proton i.e.,
(antineutrino)Since β−particle is an electron (or positron), so the loss of mass in this decay is negligible.
In β+decay the daughter element is one place forward in the periodic table.
- When a nucleus emits a gamma ray, neither the mass nor the charge of the nucleus changes
i.e., 
The gamma ray(γ-ray) is photon & it carries away some energy from the nucleus & nucleus returns from excited state(unstable state) to ground state (stable state)
α and β-particles are not emitted simultaneously.
γ rays are emitted after the emission of α and β-particle. α, β and γ-rays are known as Becquerel rays.
The energy spectrum in the case of β-particles is continuous but that of α and γ-rays is a line spectrum. This means that β particles are emitted with any amount of kinetic energy.
PROPERTIES OF α, β & γ-RAYS
(A) PROPERTIES OF α−RAYS
- It is a positively charged particle & contains a charge of 3.2 × 10–19 coulomb (exactly double the charge of electron).
- The mass of α-particles is 6.645 × 10–27kg (It is equal to mass of a helium nucleus). Actually α-particle is nucleus of helium, hence it is called doubly ionised helium.
- They (α-particles) get deflected in both electric & magnetic fields.
- The velocity of α-particle is very less than the velocity of light i.e.,
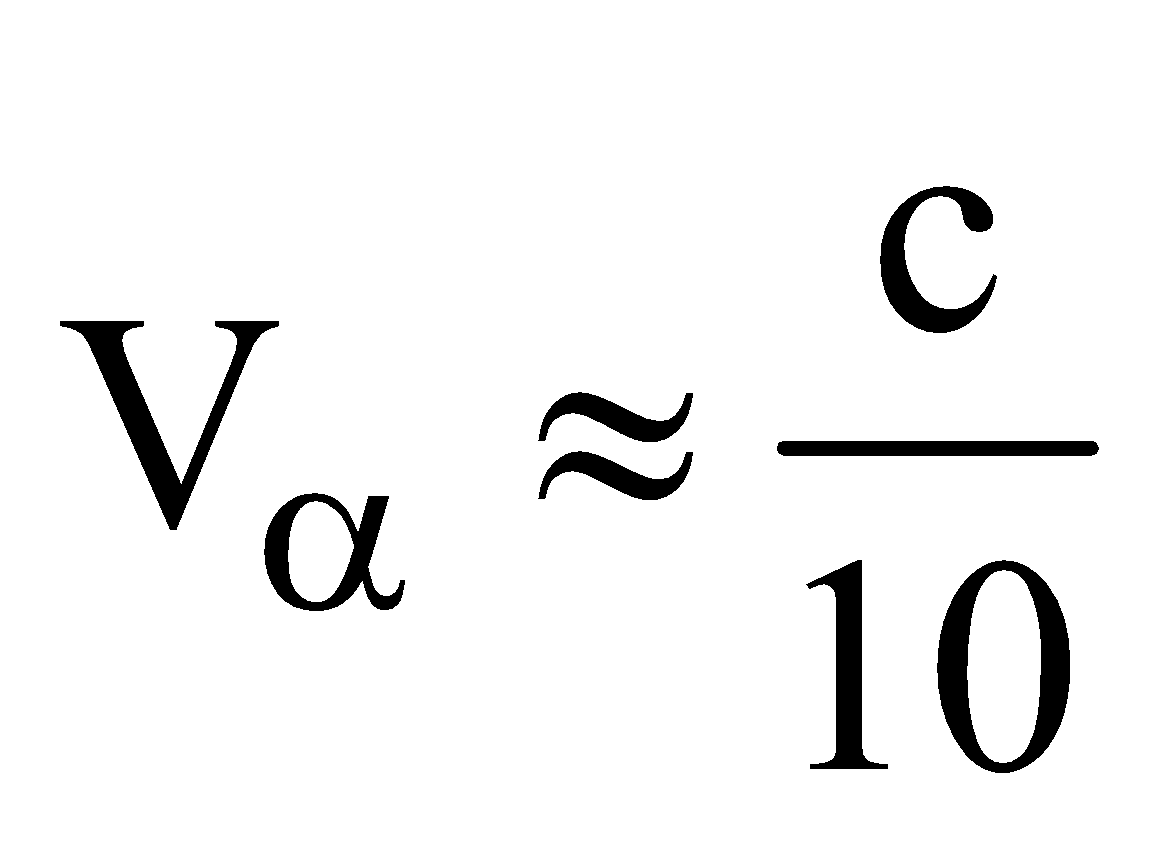, where c is velocity of light. - The range of α-particle in air depends on radioactive substance.
- The ionisation power of α-particle is higher than both β (100 times of β & 10,000 times of γ) and γ particle.
- The penetrating power of α particle is lowest (in comparison to β & γ particles). It is 1/100 times of β-particles & 1/10,000 times of γ-rays.
- The α-particles can produce fluorescence in barium platinocyanide and zinc sulphide.
- They show little effect on photographic plate.
- They show heating effect on stopping.
(B) PROPERTIES OF β-RAYS OR β-PARTICLES
- The beta particles (i.e., β– or β+) may be positive & negative particle & contain
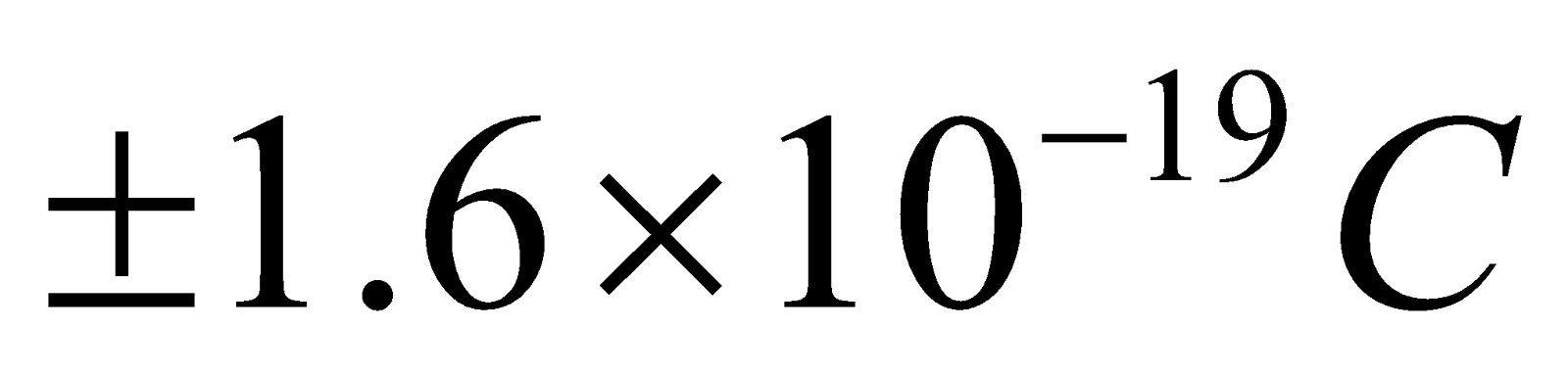of charge. Actually β– is electron & β+ is positron. - They get deflected in both electric & magnetic field.
- The velocity of β-particle varies between 0.01c to .99c, where c is velocity of light.
- The mass of β particle is relativistic, because its velocity is comparable to velocity of light
- They have both ionisation & penetration power. Ionisation power less than α-particle and penetration power more than α-particle.
- They produce fluorescence on barium platinocyanide & zinc sulphide.
(C) PROPERTIES OF γ-RAYS (OR GAMMA RADIATION)
- They are electromagnetic waves as x-rays.
- They are not deflected in electric & magnetic field, it means that they are chargeless.
- The velocity of γ-particle is equal to velocity of light.
- The ionisation power of gamma rays is less than β & α rays but penetration power more than β and α-rays.
- The γ-particles are emitted from the nucleus, while X-rays are obtained, when electron goes from one state to another in an atom.
- When γ-rays photon strikes nucleus in a substance, then it gives rise to a phenomenon of pair production i.e.,
The minimum energy of γ-rays required for this phenomena is 1.02 MeV, because the rest mass energy of 
particle is 0.51 MeV.
particle is 0.51 MeV.
RUTHERFORD AND SODDY LAW FOR RADIOACTIVE DECAY
It states that ”at any time the rate at which particular decay occurs in a radioactive substance is proportional to number of radioactive nuclei present.”
If N is the number of nuclei at any time t & at t + dt time, it decrease to N-dN then the rate of decay of these nuclei is 
(negative sign comes because N decreases as t increases). So according to Rutherford & Sodi,
(negative sign comes because N decreases as t increases). So according to Rutherford & Sodi, 
or 
…(1)Where λ is decay constant (i.e., probability per unit time for a nucleus to decay) and it is constant for a particular nuclei, but different for different nuclei. By integration of equation (1) w.r. to time we get
N = No e–λt …(2)
where No is the number of nuclei at t = 0.
Activity : The number of decays per unit time or decay rate is called activity(R)
where 
The S.I. unit of R is becquerel,
1 becquerel = 1 Bq = 1 decay/sec and 1 curie = 1 Ci = 3.7 × 1010 decay/sec
The other unit of radioactivity is rutherford.
1 rutherford = 106 decay/sec
⇒ 
m0 = mass at t =0 and m = mass at t = t
COMMON DEFAULT
🗴 Incorrect. Since β-particles (electrons) are emitted from the nucleus shows that electrons exist in nucleus
✓ Correct. β-particle cannot exists in nucleus. It is created and ejected at once at the time of β-decay. β-particle cannot exist in the nucleus because its wavelength is greater than the size of nucleus
HALF-LIFE OF A RADIOACTIVE SUBSTANCE
Half-life of a substance is the time, it takes for half of a given number of radioactive nuclei to decay
Let at = T1/2
then by eq. (2)
then by eq. (2)
or 
Also 
for n half-lives
for n half-lives⇒ 
where m0 is mass of radioactive substance at t = 0 and m is mass at t = t.
where m0 is mass of radioactive substance at t = 0 and m is mass at t = t.
MEAN LIFE OF A RADIOACTIVE SUBSTANCE
Mean life (average life) τ is defined as the average time the nucleus survive before it decays.
It is given as : 
The equivalent 
and τ for two nuclei A and B,
and τ for two nuclei A and B,
RADIOACTIVE SERIES
The heavy nuclides change their mass number by α decay and atomic number by α and β decay.
They can decay to stable end products by four paths. The four paths have mass numbers given as 4n, 4n + 1, 4n + 2, 4n + 3 where n is integer.
Last element of series is stable and has a decay constant zero.
There are four radioactive series :
Uranium 92U238 → 82Pb206
(Half life 
)
)Actinium (natural) 92U235 → 82Pb207
(Half life 
)
)Thorium 92Th232 → 82Pb208
(Half life 
)
)Neptunium 93Nb237 → 83Bi209
(Half life 
)
)But only first three series occur in nature & fourth one is artificial.
RADIOACTIVE EQUILIBRIUM
When the rate of formation of daughter nuclei becomes equal to rate of its decay then this is called as state of radioactive equilibrium
NA λA = NB λB = ………… or 
= …………
= …………CARBON DATING
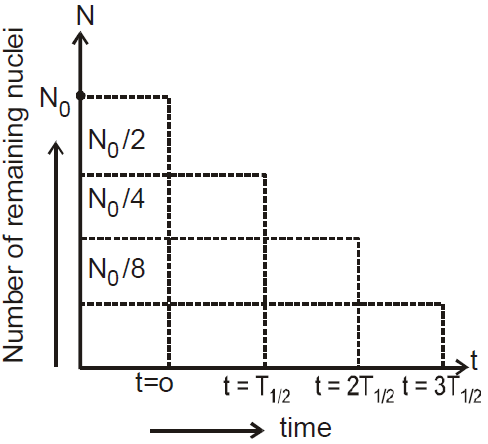
Carbon dating is the process of determination of time interval which has passed by making use of radioactive decay of a sample containing radioactive substance (6C14). It helps in calculating age of geological specimens like rocks, biological specimens likes bones of animals or trunk of trees and age of earth. The isotope of carbon 6C14 is radioactive. It is formed in atmosphere by bombardment of nitrogen atoms with cosmic rays
7N14 + 0n1 → 6C14 + 1H1
The 6C14 combines with oxygen to form carbon dioxide which is absorbed by plants so concentration of 6C14 is constant with time. The living plants and animals have a fixed ratio of 6C14 to ordinary carbon 6C12. When a plant or animal dies the content of 6C14 decreases while that of 6C12 remains constant. The ratio of two indicates the time that has passed since death of plant or animal. The time interval is calculated from the laws of radioactive disintegration
where No is number of 6C14 nuclei at time of death, λ is decay constant of 6C14 and N is number of 6C14 nuclei currently present in sample.
KEEP IN MEMORY
- Specific activity is the activity of 1 gram of material.
- Geiger Muller Counter is used for detecting α and β particles.
- Cloud chamber is used for detecting radioactive radiations and for determining their paths, range and energy.
- Baryon number
B = 1, for a neutron and a proton. - Lepton number (L)
L = 1 for electron, and neutrino
L = –1 for positron and antineutrino.
- Radioactive isotope
- Iodine-131 For detecting the activity of thyroid gland
- Chromium-51 To locate the exact position of haemorrhage
- Phosphorus-32 In agriculture
- C–14 Carbon dating, Photosynthesis in plants
- Co60 Cancer treatment
- Na24 For circulation of blood
NUCLEAR REACTION
Nuclear reaction obeys following conservation laws :
- Charge conservation
- Conservation of linear momentum
- Conservation of angular momentum
- Conservation of energy (Rest mass energy + K.E.)
Standard way of representing a nuclear reaction
For a nuclear reaction
Standard way 
NUCLEAR FISSION (BY OTTO HAHN AND STRASSMANN)
Nuclear fission is the disintegration of a heavy nucleus upon bombardment by a projectile, such that the heavy nucleus splits up into two or more segments of comparable masses with an enormous release of energy.
The most of the energy released is by the mode of kinetic energy of fission segment.
Uncontrolled Chain Reaction : It is the principle of atom bomb (destructive use). The number of fission in this case goes on increasing at a tremendous rate leading to the creation of a huge amount of energy in a very small time.
The number of fissions in this case is maintained constant.
Nuclear reactor has been devised for this purpose.
The main parts of nuclear reactor are
- Nuclear fuel : U233, U235, Pu239 etc.
- Moderator : Graphite, heavy water (D2O). To slow down the neutrons (or slow down the nuclear reaction).
- Control rods : (Cadmium, boron). To absorb excess neutrons. It controls the chain reaction.
- Coolant : (water etc). To remove the heat produced in the core to heat exchanger for production of electricity.
The reaction of controlled chain reactor is also called critical reaction.
Critical mass : It is the minimum amount of fissionable material required to carry out fission reaction. It is 10 kg for 
Reproduction factor K 
k = 1 for controlled reaction
for uncontrolled reaction
Breeder reactor :It converts U238 non-fissionable to a fissionable material Pu239 or U235.
NUCLEAR FUSION
Nuclear fusion is the fusion of two or more light nuclei to form a heavy nucleus with a release of huge amount of energy.
For a nuclear fusion to take place, very high temperature is required to overcome the coulombic repulsive forces acting between the nuclei. It is the principle of hydrogen bomb.
The nuclear fusion reaction, which is the source of the energy of sun/ star are proton-proton cycle.
Stars with mass 0.4 to 2.5 solar mass produce energy by carbon-nitrogen cycle. Stars with lower mas produce energy by proton-proton cycle.
NUCLEAR HOLOCAUST
It is the name given to large scale destruction which will be created upon the use of piled up nuclear weapons. It is believed that if the existing nuclear weapons are used, then the radioactive waste will hang like a cloud in the earth’s atmosphere. This cloud will be capable to absorb solar radiation due to which these radiation will not reach earth. This would result to a long nuclear winter.
RADIATION HAZARDS
The γ-radiations are highly energetic and causes pathological and genetic damage.
The neutrino
In the 1930s it was thought that beta minus decay was described by
\(_{0}^{1}\textrm{n} \rightarrow _{1}^{1}\textrm{p}+ \;_{{-1}}^{0}\textrm{e}\)
The mass deference for this decay is:
1.008665 u – (1.007276 + 0.0005486) u = 0.00084 u
and corresponds to an energy of:
0.00084 × 931.5 MeV = 0.783 MeV
If only the electron and the proton are produced, then the electron, being the lighter of the two, will carry most of this energy away as kinetic energy.
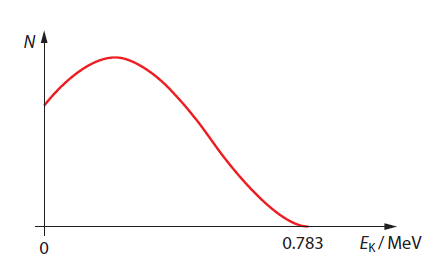
The number of electrons that carry a given energy as a function of energy.
In experiments, however, the electron has a range of energies from zero up to 0.783 MeV, If the electron is not carrying 0.783 MeV of energy, where is the missing energy?
Wolfgang Pauli hypothesised the existence of a third particle in the products of a beta decay in 1933. Since the energy of the electron in beta decay has a range of possible values, it means that a third very light particle must also be produced so that it carries the remainder of the available energy. Enrico Fermi coined the word neutrino for the ‘little neutral one.
Tunneling Through a Potential Barrier
A potential energy barrier is a region where a traveling particle will have an increased potential energy Ub.
The particle can pass through the barrier if its total energy \(E>U_b\).
Classically, it cannot pass through it if \(E<U_b\)., but in quantum physics it can, an effect called tunneling.
For a particle with mass m and a barrier of thickness L, the transmission coefficient is
\(T\approx e^{-2bL}\)
where
\(b=\sqrt{\frac{8\pi ^2 m(U_b-E)}{h^2}}\)
Can the electron pass through the region of negative potential?
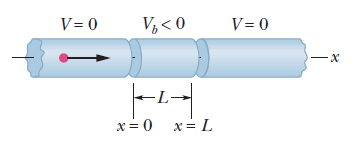
The elements of a narrow tube in which an electron (the dot) approaches a negative electric potential Vb in the region x= 0 to x= L.
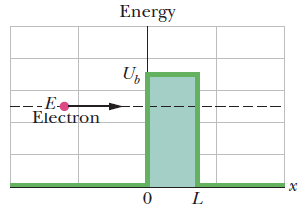
An energy diagram containing two plots for the situation of Fig. above:
- The electron’s mechanical energy E is plotted when the electron is at any coordinate x < 0.
- The electron’s electric potential energy U is plotted as a function of the electron’s position x, assuming that the electron can reach any value of x.
- The nonzero part of the plot (the potential barrier) has height Ub and thickness L.
plot of the probability density \(|\Psi|^2\) of the electron matter wave for the situation of first Fig.The value of \(|\Psi|^2\) is nonzero to the right of the potential barrier.