IB PHYSICS SL (Standard level)- 2024 – Practice Questions- All Topics
Topic 4.3 – Wave characteristics
Topic 4 Weightage : 10 %
All Questions for Topic 4.3 – Wavefronts and rays , Amplitude and intensity , Superposition , Polarization
Question
Two identical waves, each with amplitude X0 and intensity I, interfere constructively. What are the amplitude and intensity of the resultant wave?

▶️Answer/Explanation
Ans: D
Question
A beam of unpolarized light is incident on the first of two parallel polarizers. The transmission axes of the two polarizers are initially parallel.
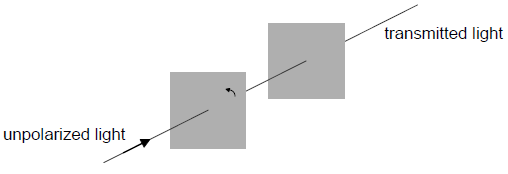
The first polarizer is now rotated about the direction of the incident beam by an angle smaller than 90°. Which gives the changes, if any, in the intensity and polarization of the transmitted light?
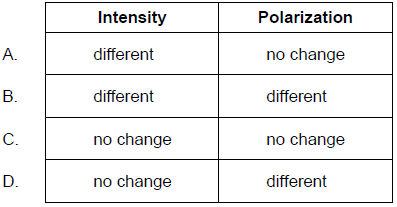
▶️Answer/Explanation
Markscheme
A
Ref :https://www.iitianacademy.com/ib-dp-physics-topic-4-waves-4-3-wave-characteristics-study-notes/
Intensity of light changes but still it remained polarised.
Question
Two wave pulses, each of amplitude A, approach each other. They then superpose before continuing in their original directions. What is the total amplitude during superposition and the amplitudes of the individual pulses after superposition?
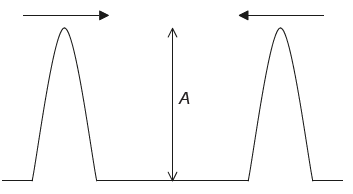
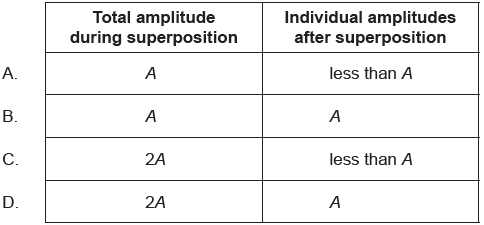
▶️Answer/Explanation
Markscheme
D
When two or more waves simultaneously pass through a point, the disturbance at the point is given by the sum of the disturbances each wave would produce in absence of the other wave(s).
The displacement of the particles, if the first wave alone were travelling, may be written as
\(y_1=f_1(t-x/v)\)
and the displacement if the second wave alone were travelling may be written as
\(y_2=f_2(t+x/v)\)
\(y=y_1+y_2 =y_1=f_1(t-x/v) + y_2=f_2(t+x/v)\)

Question
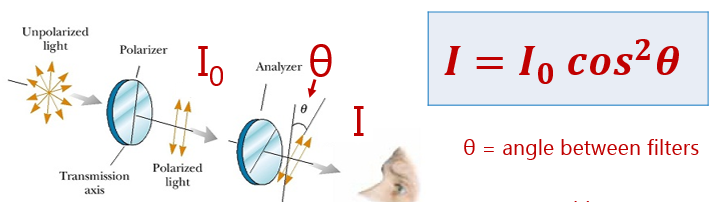
Unpolarized light of intensity I0 is incident on the first of two polarizing sheets. Initially the planes of polarization of the sheets are perpendicular.
Which sheet must be rotated and by what angle so that light of intensity \(\frac{{{I_0}}}{4}\) can emerge from the second sheet?
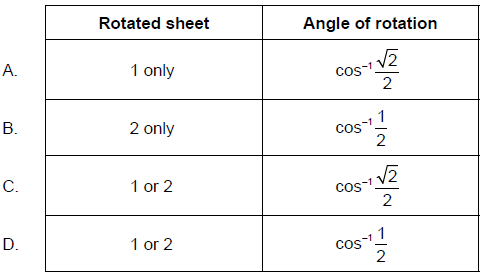
▶️Answer/Explanation
Markscheme
C
According to Malus’ law, when the unpolarized light with intensity I0 is incident on the first polarizer, the polarizer polarizes this incident light. The intensity of light becomes
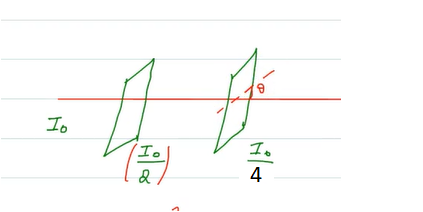
\(I_1=\frac{I_0}{2}\)
\(Now \; I_2 = I_1 cos^2\theta\)
\(I_2 =\frac{I_0}{2}cos^2\theta\)
\(\because I_2 =\frac{I_0}{4}\)
\(\frac{I_0}{4} =\frac{I_0}{2}cos^2\theta\)
\(\therefore cos\theta =\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\)
\(\theta = cos^{-1}\frac{\sqrt{2}}{2}\)
And Either Sheet can rotate with affecting the result.
Question
Horizontally polarized light of intensity I0 enters a polarizer P whose polarization axis makes an angle of θ degrees with the horizontal. Light from P is then incident on a polarizer A with fixed vertical polarization axis.
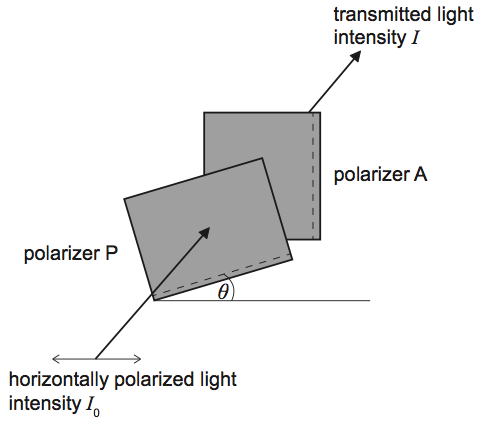
The angle θ is varied from 0 to 90 degrees. Which of the following represents the variation with θ of the intensity I of the light transmitted through A?
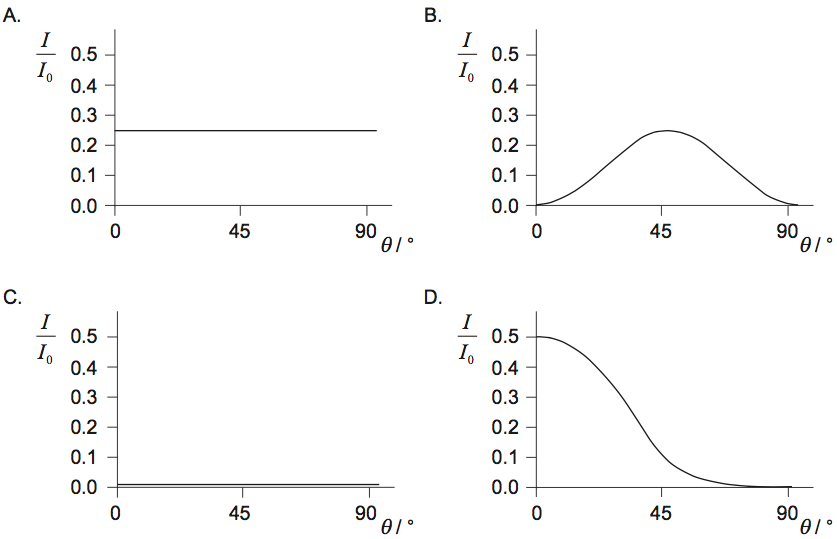
▶️Answer/Explanation
Markscheme
B
\( \; I_2 = I_1 cos^2\theta\)
\(I_1=\frac{I_0}{2}\)
\(\therefore I_2=\frac{I_0}{2} cos^2(90-\theta )=\frac{I_0}{2} sin^2 \theta\)
Option B is graph of \(sin^2 \theta\)
Question
A water wave moves on the surface of a lake. P and Q are two points on the water surface. The wave is traveling towards the right.
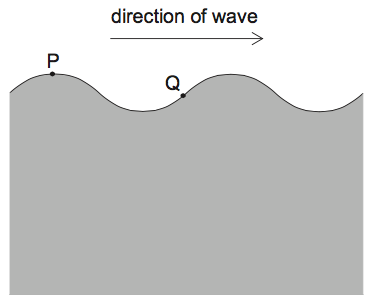
The diagram shows the wave at time t = 0. Which graph shows how the displacements of P and Q vary with t?
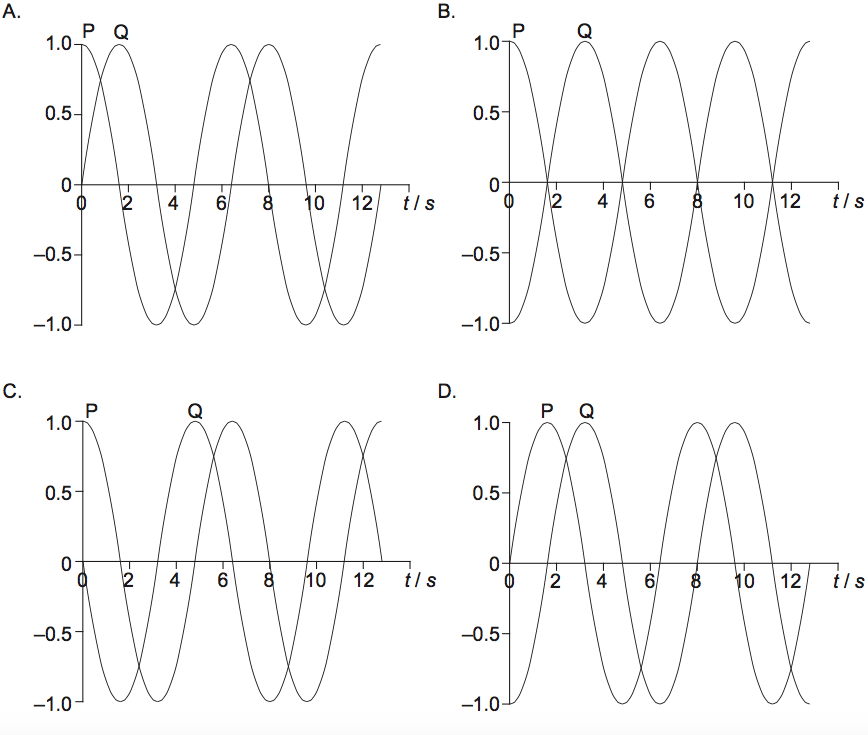
▶️Answer/Explanation
Markscheme
C

Path difference between point P and Q is =\(\frac{\lambda }{2}+\frac{\lambda }{4}=\frac{3\lambda }{4}\)
Phase difference = \(\phi =\frac{2\pi}{\lambda}\times \frac{3 \lambda}{4}= 1.5 \pi\)
Option C has phase diff of \(1.5 \pi\)
P has maximum displacement and Q is at Zero displacement
Question
A particle P executes simple harmonic motion (SHM) about its equilibrium position Y.
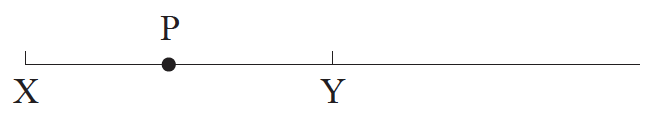
The amplitude of the motion is XY.
At which of the positions shown on the diagram is the acceleration of P equal to zero and the kinetic energy of P equal to zero?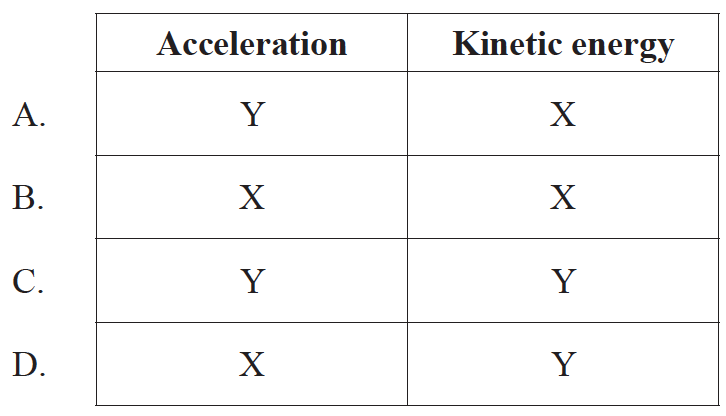
▶️Answer/Explanation
Markscheme
A
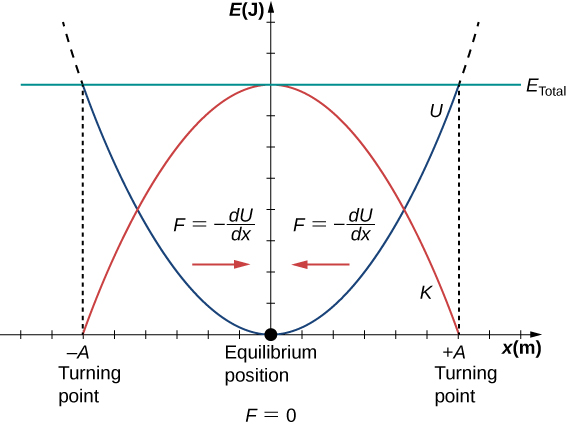
Force is zero at Equilibrium position and kinetic energy is zero at extreme position.
