1.3 Vectors and scalars
Essential Idea:
Some quantities have direction and magnitude, others have magnitude only, and this understanding is the key to correct manipulation of quantities. This subtopic will have broad applications across multiple fields within physics and other sciences.
Understandings:
- Vector and scalar quantities
- Combination and resolution of vectors
Applications and Skills:
- Solving vector problems graphically and algebraically
SCALARS AND VECTORS
Scalars : The physical quantities which have only magnitude but no direction, are called scalar quantities.
For example – distance, speed, work, temperature, mass, etc.
Scalars are added, subtracted, multiplied and divided by ordinary laws of algebra.
Vectors : For any quantity to be a vector,
- it must have magnitude.
- it must have direction.
- it must satisfy parallelogram law of vector addition.
For example – displacement, velocity, force, etc.
Note – Electric current has magnitude as well as direction but still it is not treated as a vector quantity because it is added by ordinary law of algebra.
TYPES OF VECTORS
LIKE VECTORS
Vectors having same direction are called like vectors. The magnitude may or may not be equal.
EQUAL VECTORS
Vectors having same magnitude and same direction are called equal vectors.
Here  and
and  are equal vectors
are equal vectors  =
= 
Thus, equal vector is a special case of like vector.
UNLIKE VECTORS
Vectors having exactly opposite directions are called unlike vectors.
The magnitude may or may not be equal.
NEGATIVE VECTORS
Vectors having exactly opposite direction and equal magnitudes are called negative vectors.
Here  and
and  are negative vectors,
are negative vectors,  = –
= –
Thus negative vectors is a special case of unlike vectors.
UNIT VECTOR
Vector which has unit magnitude. It represents direction only. For example take a vector . Unit vector in the direction of
. Unit vector in the direction of  is
is 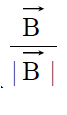 , which is denoted as
, which is denoted as .
.  , is read as “B cap” or “B caret”.
, is read as “B cap” or “B caret”.
ORTHOGONAL UNIT VECTOR
A set of unit vectors, having the directions of the positive x, y and z axes of three dimensional rectangular coordinate system are denoted by  . They are called orthogonal unit vectors because angle between any of the two unit vectors is 90º.
. They are called orthogonal unit vectors because angle between any of the two unit vectors is 90º.
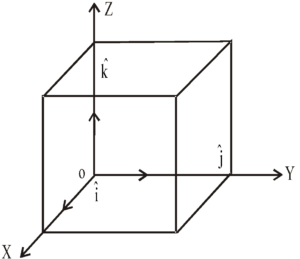
The coordinate system which has shown in fig. is called right handed coordinate system. Such a system derives its name from the fact that right threaded screw rotated through 90º from OX to OY will advance in positive Z direction as shown in the figure.
NULL VECTOR (ZERO VECTOR)
A vector of zero magnitude is called a zero or null vector. Its direction is not defined. It is denoted by 0.
Properties of Null or Zero Vector :
- The sum of a finite vector and the zero vector is equal to the finite vector
i.e., 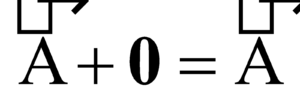
- The multiplication of a zero vector by a finite number n is equal to the zero vector
i.e., 0 n = 0
- The multiplication of a finite
 by a zero is equal to zero vector
by a zero is equal to zero vector
i.e., 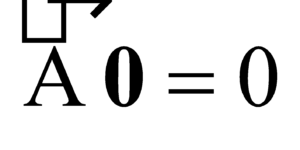
AXIAL VECTOR
Vector associated with rotation about an axis i.e., produce rotation effect is called axial vector. Examples are angular velocity, angular momentum, torque etc.
COPLANAR VECTORS
Vectors in the same plane are called coplanar vectors.
POSITION VECTORS AND DISPLACEMENT VECTORS
The vector drawn from the origin of the coordinate axes to the position of a particle is called position vector of the particle. If A (x1, y1, z1) and B (x2, y2, z2) be the positions of the particle at two different times of its motion w.r.t. the origin O, then position vector of A and B are
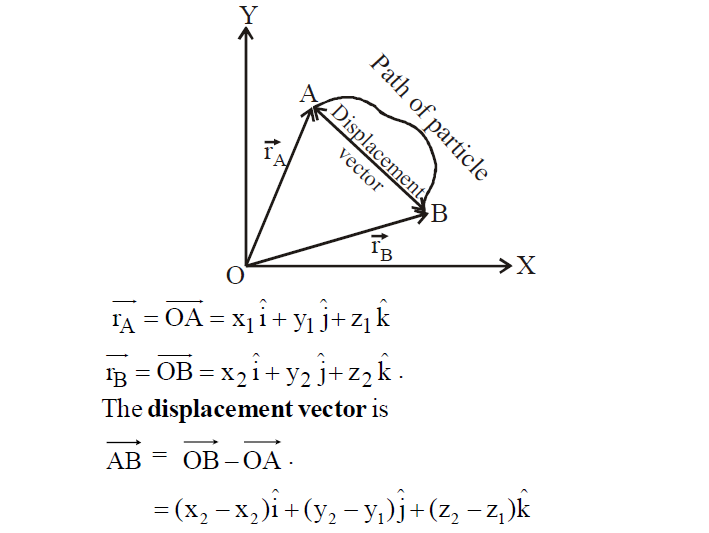
LAWS OF VECTOR ALGEBRA
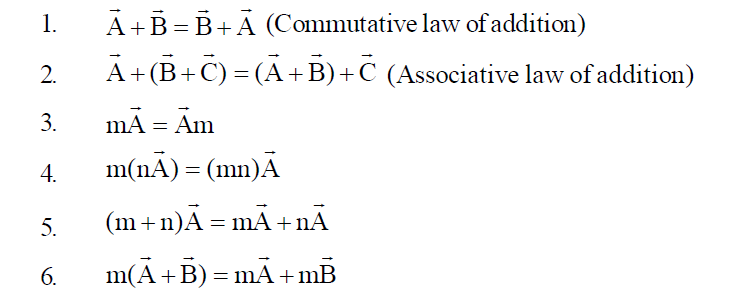
ADDITION OF VECTORS
TRIANGLE LAW OF VECTOR ADDITION
It states that if two vectors acting on a particle at the same time are represented in magnitude and direction by the two sides of a triangle taken in one order, their resultant vector is represented in magnitude and direction by the third side of the triangle taken in opposite order.
Magnitude of  is given by
is given by 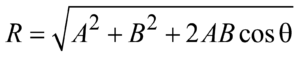
where  is the angle between
is the angle between  and
and .
.

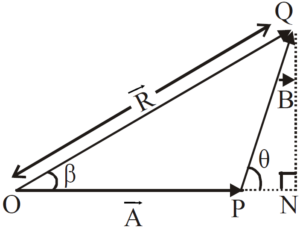
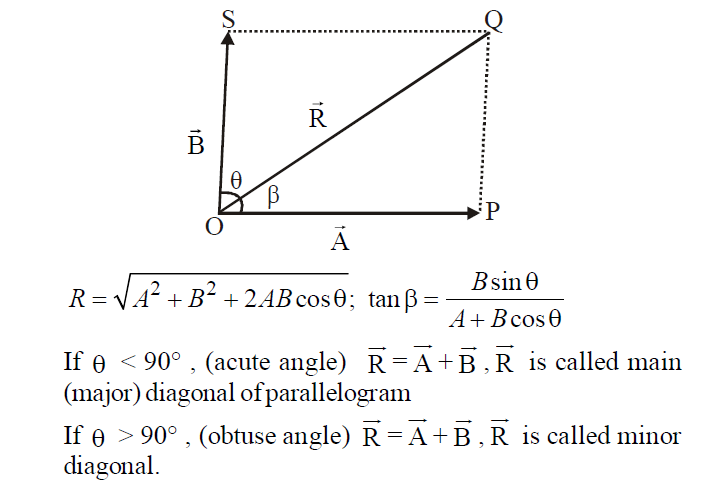
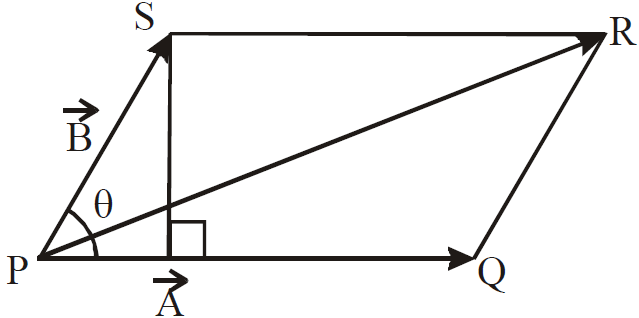
PARALLELOGRAM LAW OF VECTOR ADDITION
It states that if two vectors are represented in magnitude and direction by the two adjacent sides of a parallelogram then their resultant is represented in magnitude and direction by the diagonal of the parallelogram.
Let the two vectors  and
and ., inclined at angle
., inclined at angle  are represented by sides OP and OQ of parallelogram OPQS, then resultant vector
are represented by sides OP and OQ of parallelogram OPQS, then resultant vector  is represented by diagonal OQ of the parallelogram.
is represented by diagonal OQ of the parallelogram.
POLYGON LAW OF VECTOR ADDITION
If a number of non zero vectors are represented by the (n–1) sides of an n-sided polygon then the resultant is given by the closing side or the nth side of the polygon taken in opposite order.
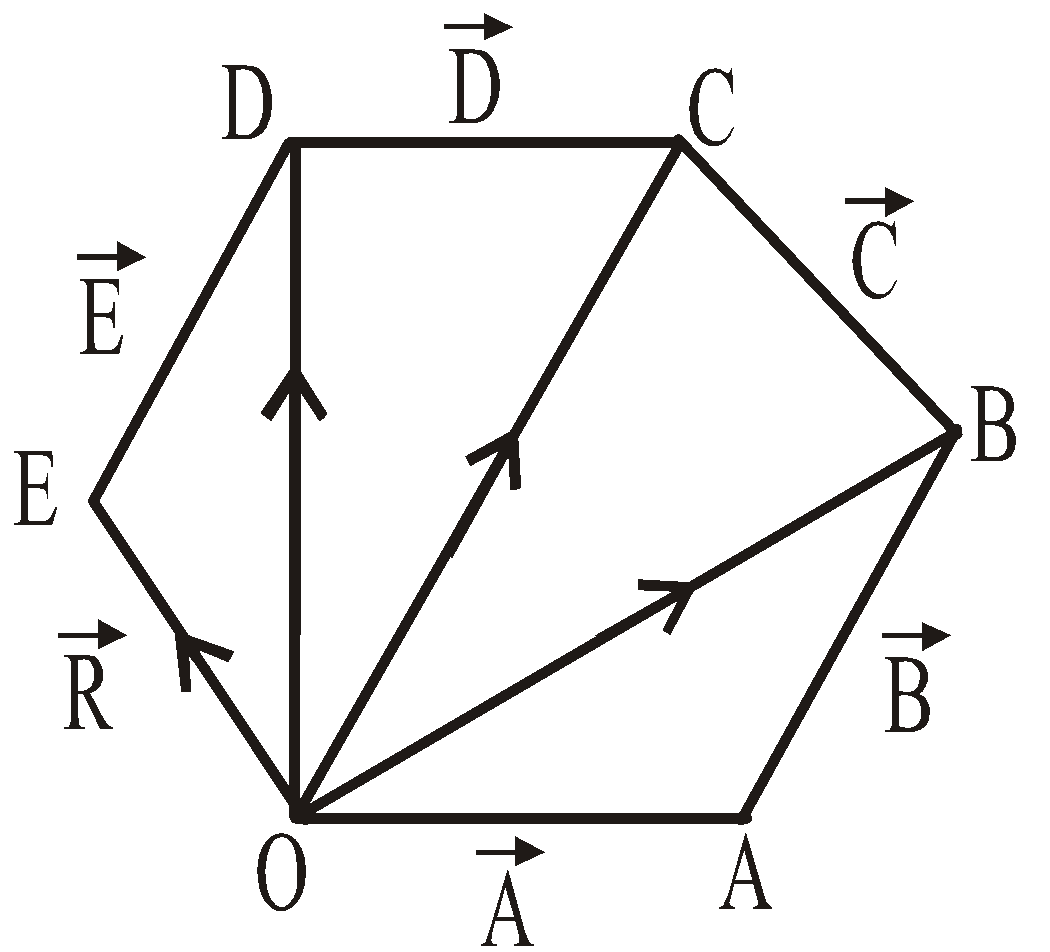
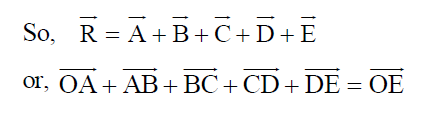
Note:
- Resultant of two unequal vectors cannot be zero.
- Resultant of three coplanar vectors may or may not be zero.
- Minimum no. of coplanar vectors for zero resultant is 2 (for equal magnitude) and 3 (for unequal magnitude).
- Resultant of three non coplanar vectors cannot be zero. Minimum number of non coplanar vectors whose sum can be zero is four.
- Polygon law should be used only for diagram purpose for calculation of resultant vector (For addition of more than 2 vectors) we use components of vector.
KEEP IN MEMORY

- A vector can be divided or multiplied by a scalar.
- Vectors of the same kind can only be added or subtracted. It is not possible to add or subtract the vectors of different kind. This rule is also valid for scalars.
- Vectors of same as well as different kinds can be multiplied.
- A vector can have any number of components. But it can have only three rectangular components in space and two rectangular components in a plane. Rectangular components are mutually perpendicular.
- The minimum number of unequal non-coplanar whose vector sum is zero is 4.

SUBTRACTION OF VECTORS
We convert vector subtraction into vector addition.
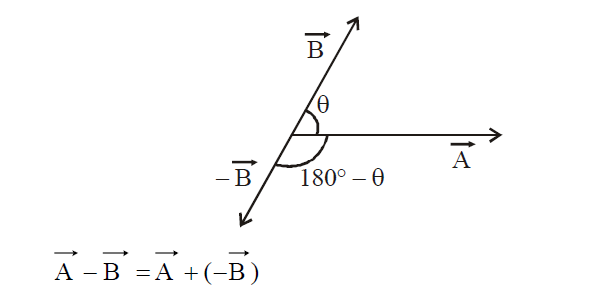
If the angle between and is θ then the angle between
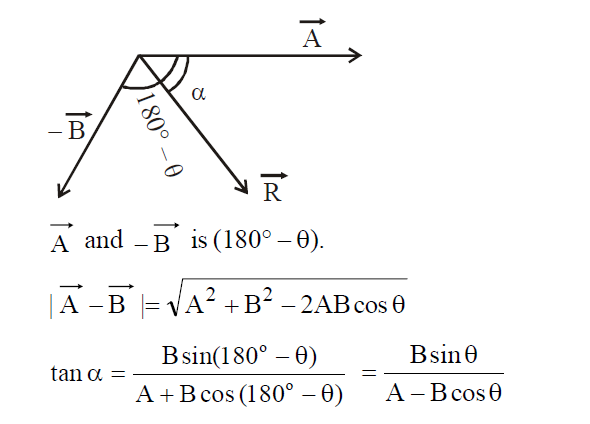
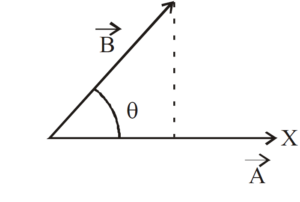
RESOLUTION OF A VECTOR
RECTANGULAR COMPONENTS OF A VECTOR IN PLANE
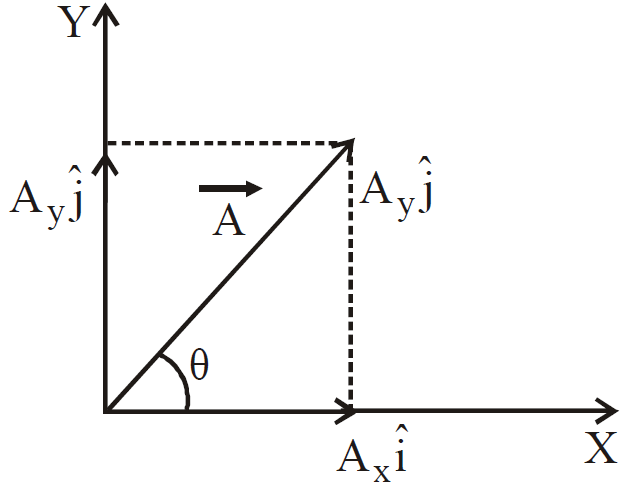
The vector  may be written as
may be written as  = Ax i + Ay j
= Ax i + Ay j
where Ax i is the component of vector  in X-direction and Ay j is the component of vector in the Y-direction.
in X-direction and Ay j is the component of vector in the Y-direction.
Also Ax = A cos θ and Ay = A sin θ
⇒ A cos θ and A sin θ are the magnitudes of the components of  in X and Y-direction respectively.
in X and Y-direction respectively.
Also 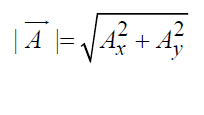
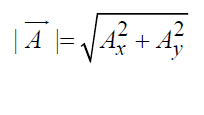
RECTANGULAR COMPONENTS OF A VECTOR IN 3D
Three rectangular components along X, Y and Z direction are given by Ax i, Ay j, Az k Therefore, vector may be written as
If ∝, β and γ are the angles subtended by the rectangular components of vector then
cos ∝ = 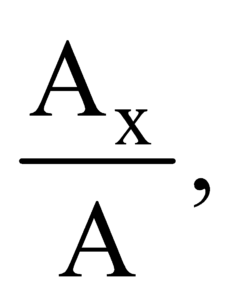 cos β =
cos β = 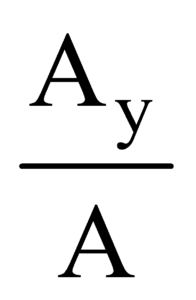 and cos γ=
and cos γ= 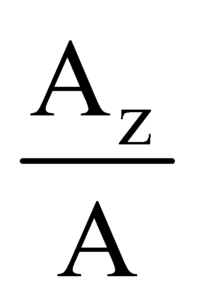
Also, cos2 ∝+ cos2 β+ cos2 γ = 1
CAUTION
Do not resolve the vector at its head.
Do not resolve the vector at its head.
The vector is always resolved at its tail.
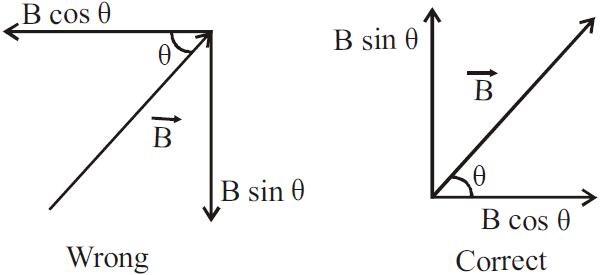
PRODUCT OF TWO VECTORS
SCALAR OR DOT PRODUCT
The scalar or dot product of two vectors A and B is a scalar, which is equal to the product of the magnitudes of and and cosine of the smaller angle between them.
i.e.,  .
. = A B cosθ
= A B cosθ
e.g. 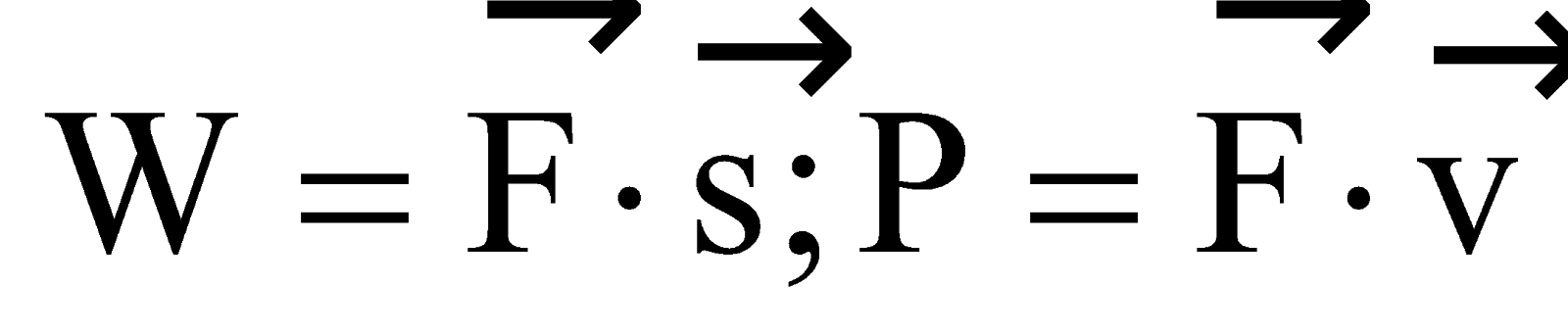
PROPERTIES OF SCALAR OR DOT PRODUCT
 .
. = A (B cosθ) = B (A cosθ)
= A (B cosθ) = B (A cosθ)
The dot product of two vectors can be interpreted as the product of the magnitude of one vector and the magnitude of the component of the other vector along the direction of the first vector.
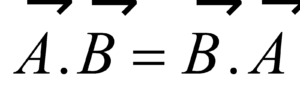 Dot product of two vectors is commutative.
Dot product of two vectors is commutative.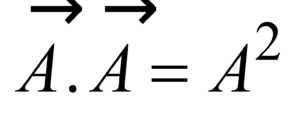
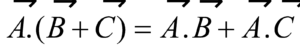 Dot product is distributive.
Dot product is distributive. 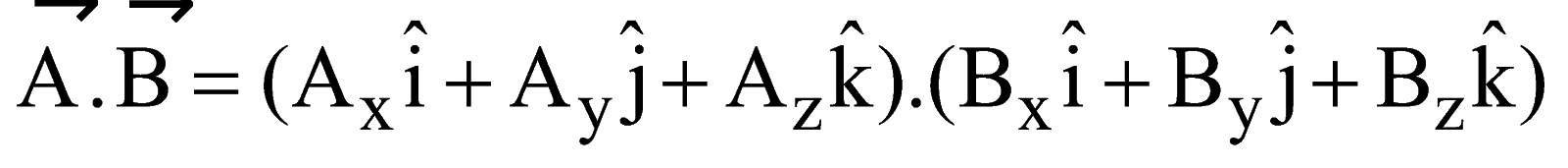 = (Ax Bx + Ay By + Az Bz)
= (Ax Bx + Ay By + Az Bz)
VECTOR OR CROSS PRODUCT
The vector product of two vectors is defined as a vector having magnitude equal to the product of two vectors and sine of the angle between them. Its direction is perpendicular to the plane containing the two vectors (direction of the vector is given by right hand screw rule or right hand thumb rule.
The direction of 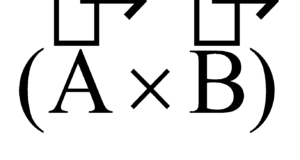 perpendicular to the plane containing vectors
perpendicular to the plane containing vectors  and
and  in the sense of advance of a right handed screw rotated from
in the sense of advance of a right handed screw rotated from  to
to  is through the smaller angle between them.
is through the smaller angle between them.
PROPERTIES OF VECTOR OR CROSS PRODUCT

- The cross product of two vectors represents the area of the parallelogram formed by them.
= area of parallelogram PQRS
= 2 (area of ΔPQR)
- A unit vector which is perpendicular to A as well as B is
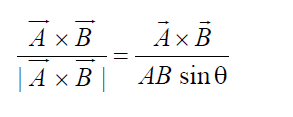
KEEP IN MEMORY
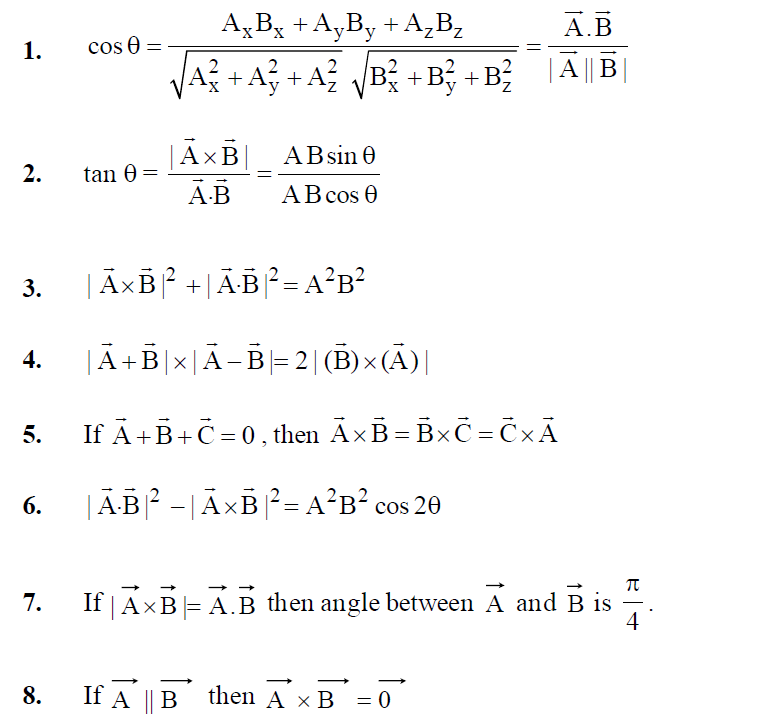
Division by a vector is not defined. Because, it is not possible to divide by a direction.
The sum and product of vectors is independent of coordinate axes system.
CONDITION OF ZERO RESULTANT VECTOR
If the three vectors acting on a point object at the same time are represented in magnitude and direction by the three sides of a triangle taken in order, then their resultant is zero and the three vectors are said to be in equilibrium.
i.e. 
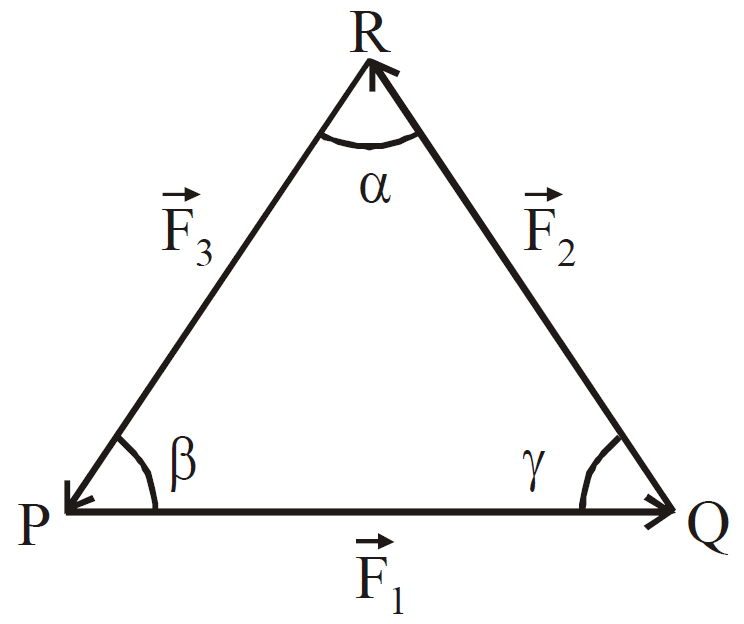
LAMI’S THEOREM
It states that if three forces acting at a point are in equilibrium, then each force is proportional to the sine of the angle between the other two forces.
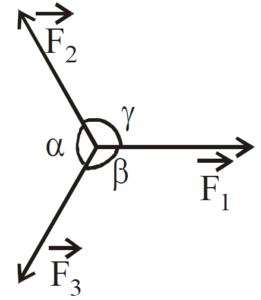
or, 
MOTION IN A PLANE OR MOTION IN TWO DIMENSIONS
The motion in which the movement of a body is restricted to a plane is called motion in a plane.
Example : A ball is thrown with some initial velocity (u) and making angle θ with horizontal.
The general approach to solve problem on this topic is to resolve the motion into two mutually perpendicular coordinates. One along X-axis and other along Y-axis. These two motions are independent of each other and can be treated as two separate rectilinear motions.
The velocity v and acceleration a can be resolved into its x and y components.
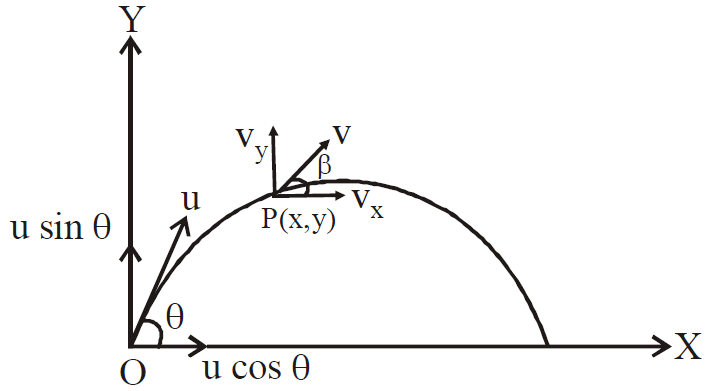
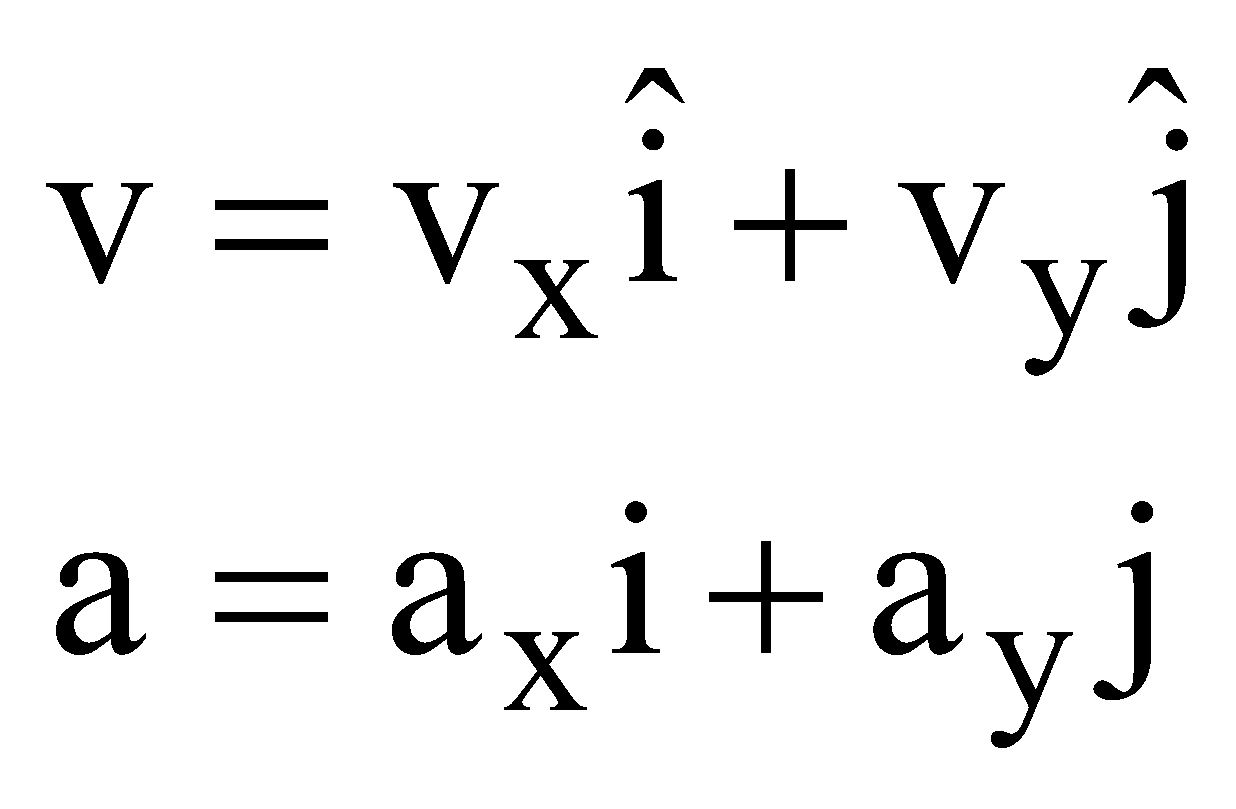
x-component of motion y- component of motion
vx = ux + axt vy = uy + ayt
x = ux t + axt2 y = uyt +
axt2 y = uyt + ayt2
ayt2
vx2 – ux2 = 2 axx vy2 – uy2 = 2 ayy
x = 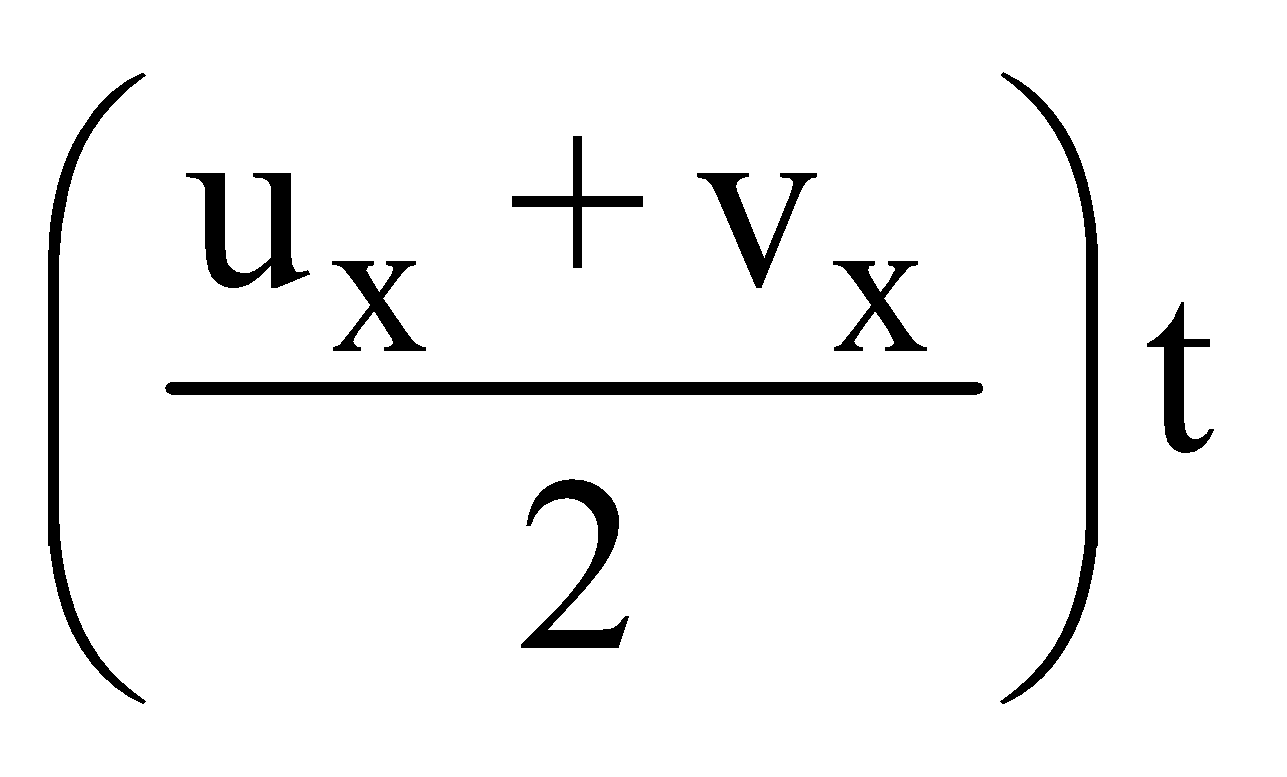 y =
y = 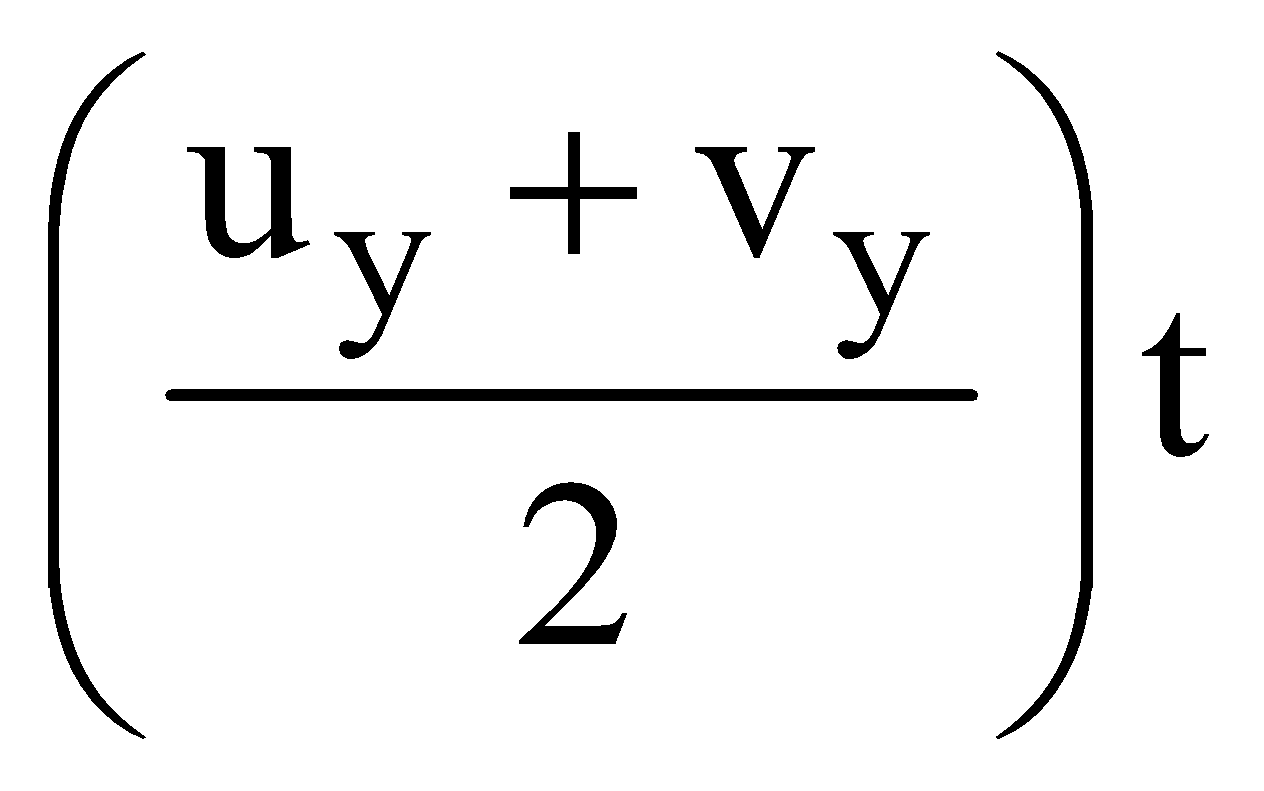
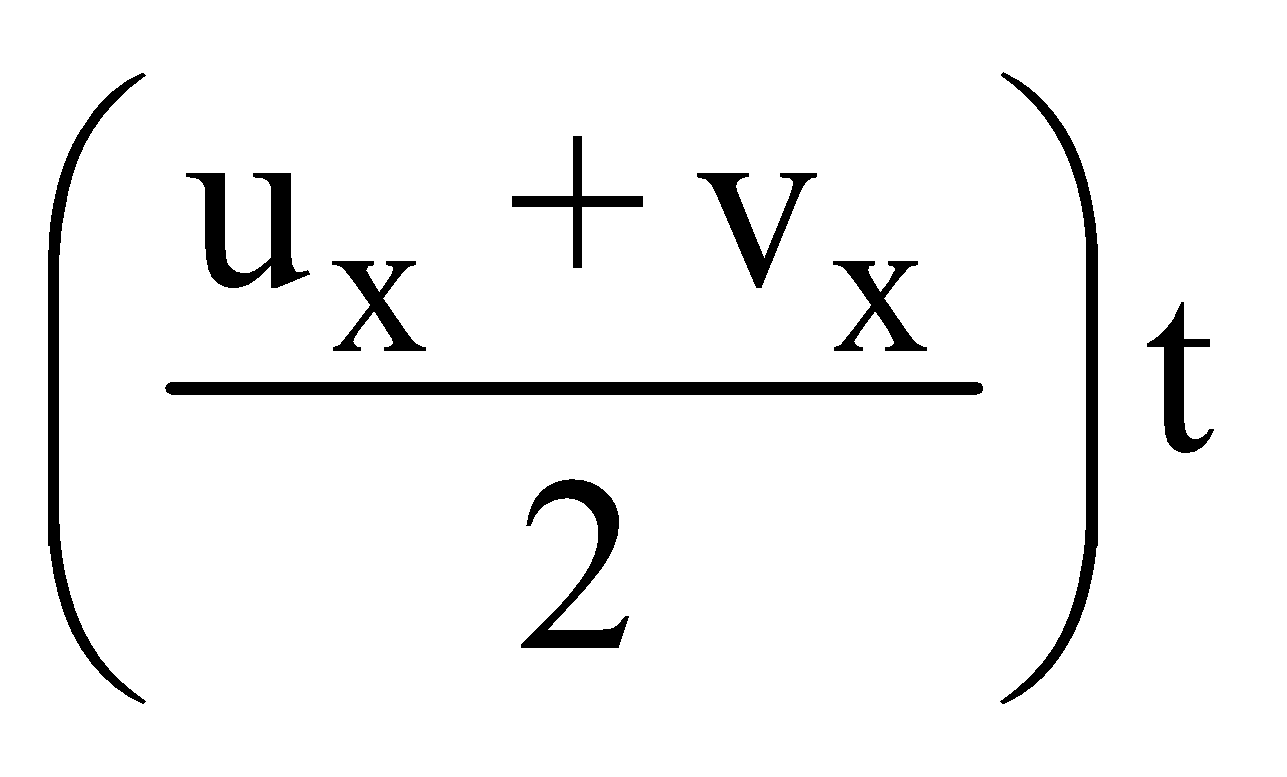 y =
y = 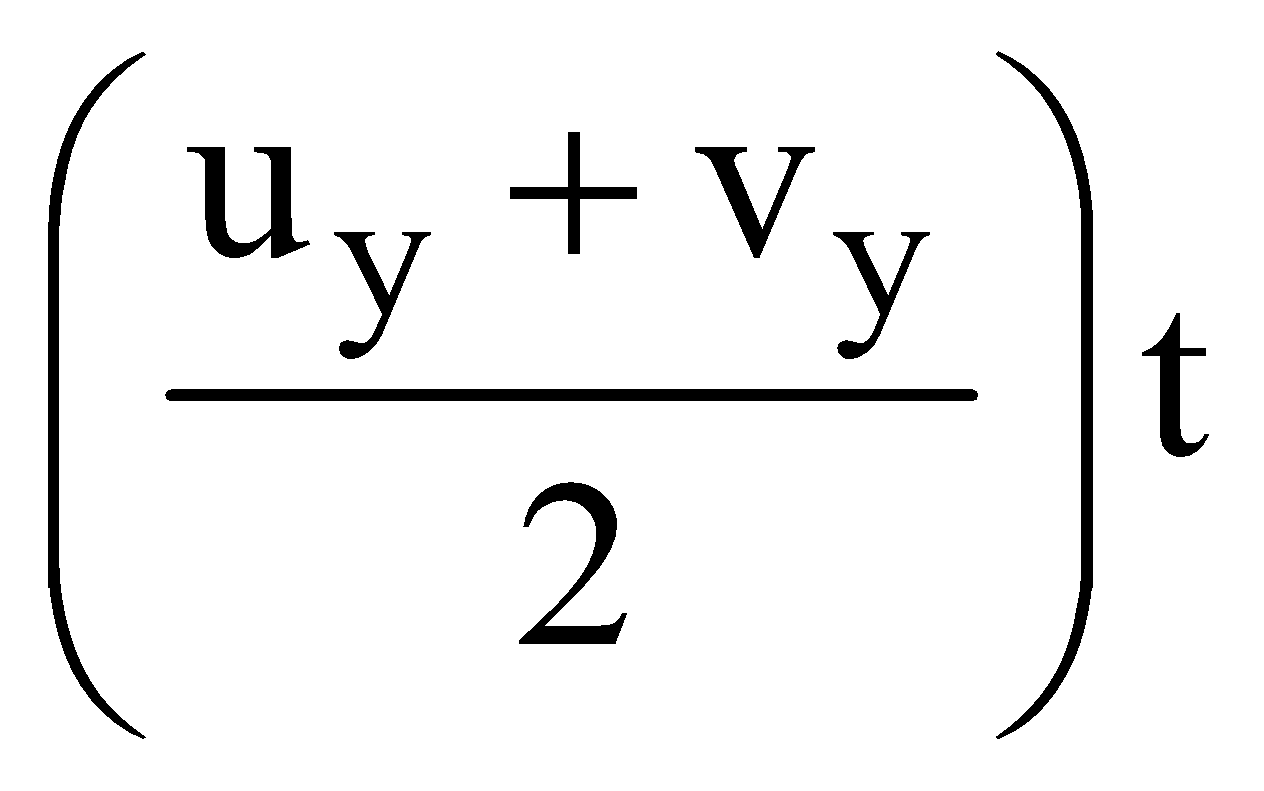
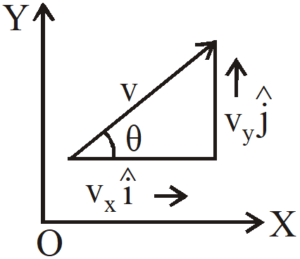
VELOCITY
The ratio of the displacement and the corresponding time interval is called the average velocity.
Average velocity 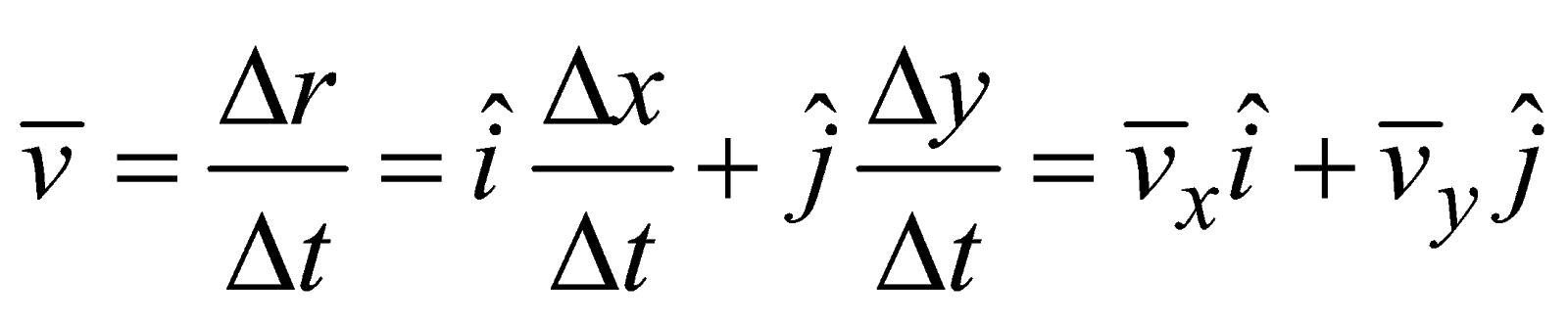
Instantaneous velocity 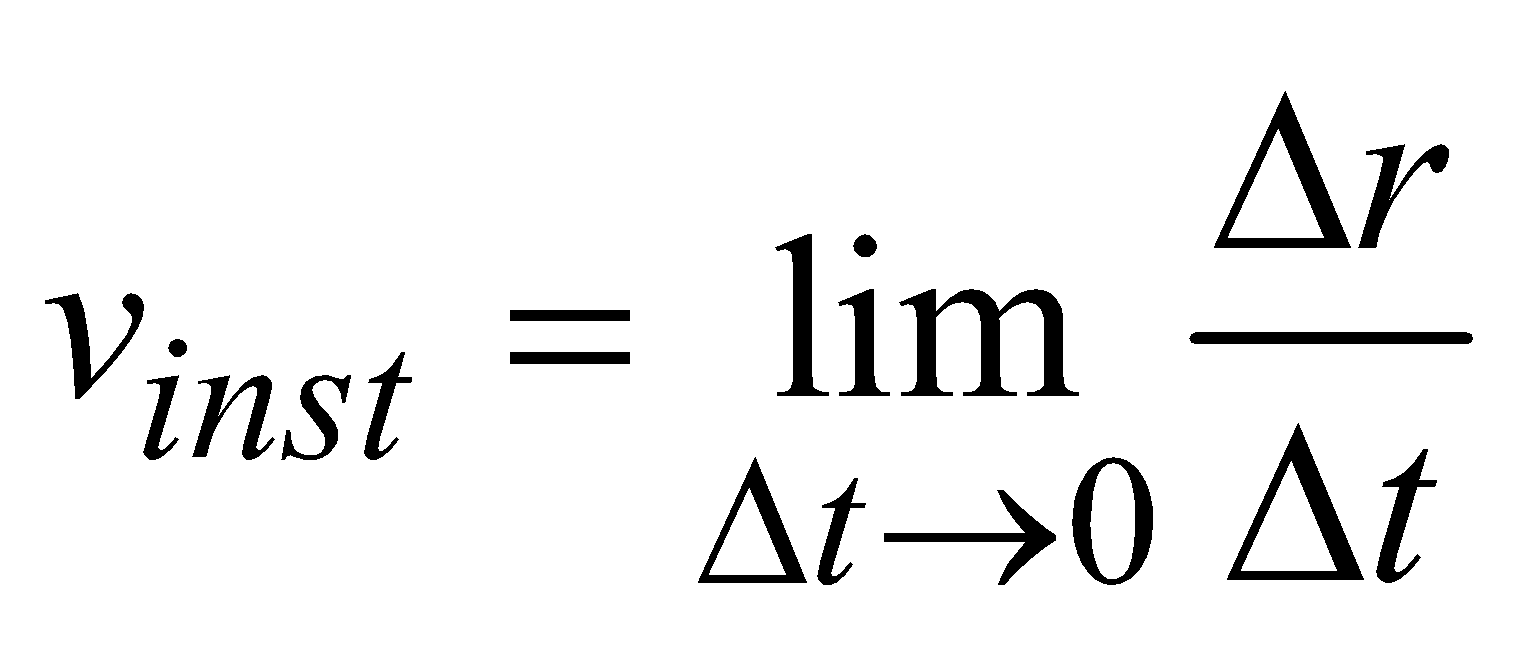
The magnitude of v = 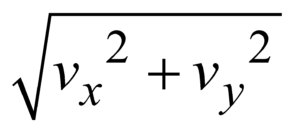
The direction of the velocity, 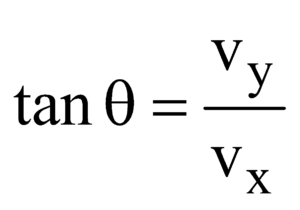 ∴
∴ 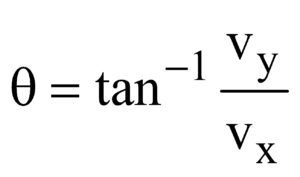
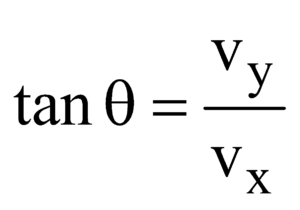 ∴
∴ 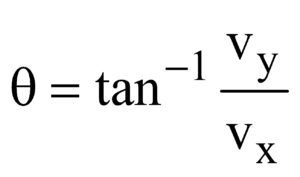
ACCELERATION
The average acceleration in a x–y plane in time interval Δt is the change in velocity divided by the time interval.
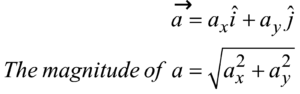
Average acceleration 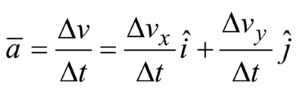
Instantaneous acceleration 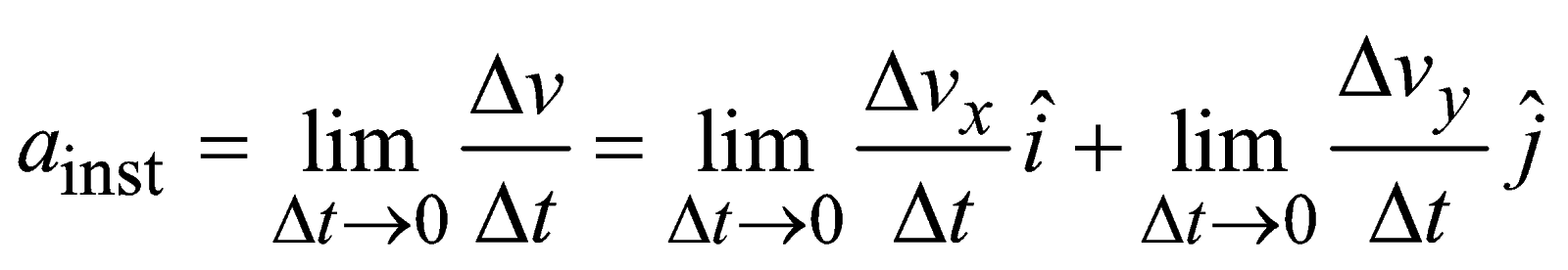
In two or three dimensions, the velocity and acceleration vectors may have any angle between 0°and 180° between them.
RELATIVE VELOCITY IN TWO DIMENSIONS
If two objects A and B moving with velocities VA and VB with respect to some common frame of reference, then :
- Relative velocity of A w.r.t B
- Relative velocity of B w.r.t. A
Therefore, VAB =- VBA and 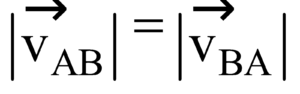
PROJECTILE MOTION
Projectile is the name given to a body thrown with some initial velocity in any arbitrary direction and then allowed to move under the influence of gravity alone.
Examples : A football kicked by the player, a stone thrown from the top of building, a bomb released from a plane.
The path followed by the projectile is called a trajectory.
The projectile moves under the action of two velocities:
- A uniform velocity in the horizontal direction, which does not change (if there is no air resistance)
- A uniformly changing velocity in the vertical direction due to gravity.
The horizontal and vertical motions are independent of each other.
TYPES OF PROJECTILE
- Oblique projectile : In this, the body is given an initial velocity making an angle with the horizontal and it moves under the influence of gravity along a parabolic path.
- Horizontal projectile : In this, the body is given an initial velocity directed along the horizontal and then it moves under the influence of gravity along a parabolic path.
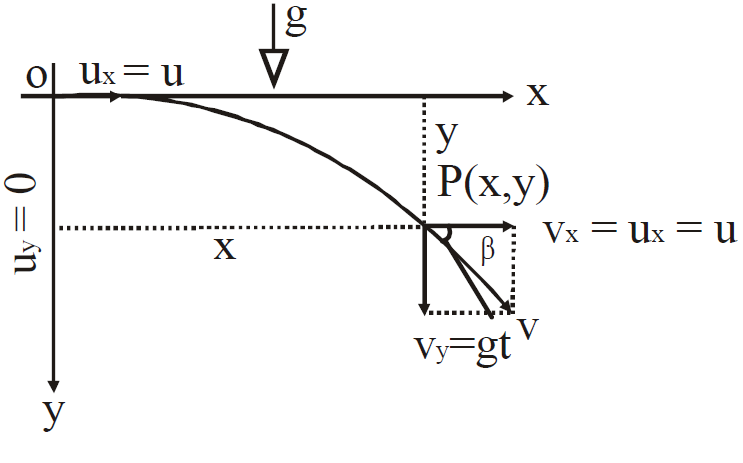
MOTION ALONG X-AXIS
ux = u, ax = 0
x = uxt +  axt2
axt2
x = ut + 0
∴ t = x/u …… (1)
MOTION ALONG Y-AXIS
uy = 0, ay = g
y = uyt +  ayt2 ⇒ 0 +
ayt2 ⇒ 0 +  gt2
gt2
y = gt2 …… (2)
gt2 …… (2)
From equations (1) and (2) we get y = 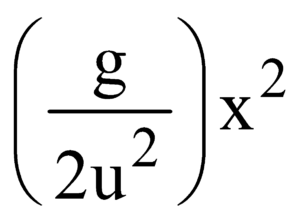 which is the equation of a parabola.
which is the equation of a parabola.
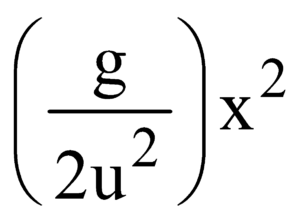 which is the equation of a parabola.
which is the equation of a parabola.VELOCITY AT ANY INSTANT
v = 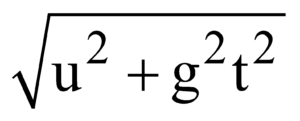
If β is the angle made by with the horizontal, then
tanβ = 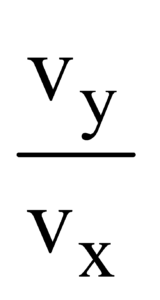 =
= 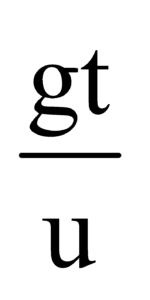
TIME OF FLIGHT AND HORIZONTAL RANGE
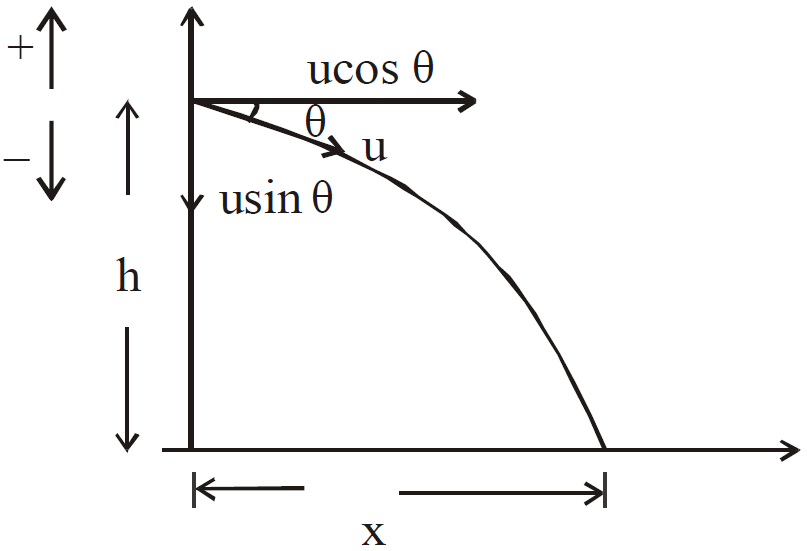
If h is the distance of the ground from the point of projection, T is the time taken to strike the ground and R is the horizontal range of the projectile then
T = 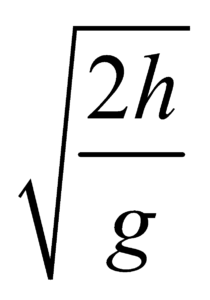 and
and 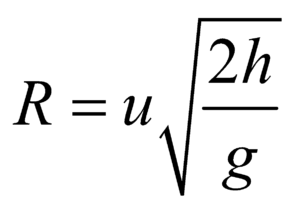
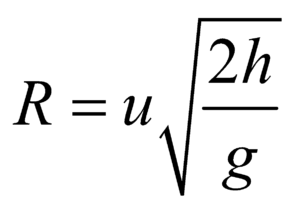
Case 1 : If the projectile is projected from the top of the tower of height ‘h’, in horizontal direction, then the height of tower h, range x and time of flight t are related as :

Case 2 : If a particle is projected at an angle (θ) in upward direction from the top of tower of height h with velocity u, then
uy = u sin θ
ay = – g
ux = u cos θ
ax = 0
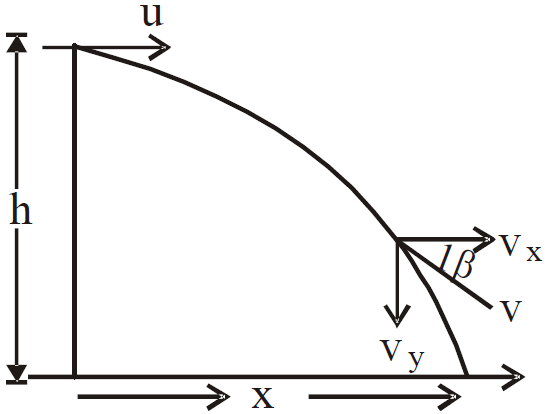
Case 3 : If a body is projected at an angle (θ) from the top of tower in downward direction then
uy = – u sin θ, ux = u cosθ, ax = 0
ay = 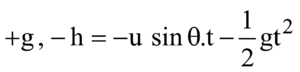 and x = u cosθ.t
and x = u cosθ.t
EQUATION OF TRAJECTORY
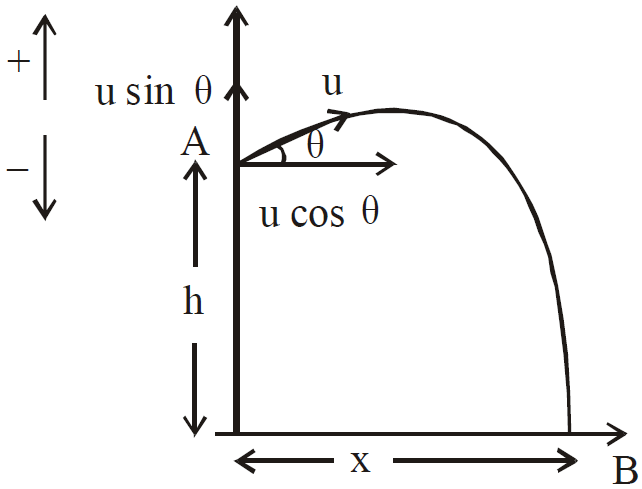
Let the point from which the projectile is thrown into space is taken as the origin, horizontal direction in the plane of motion is taken as the X-axis, the vertical direction is taken as the Y-axis, Let the projectile be thrown with a velocity u making an angle θ with the X-axis.
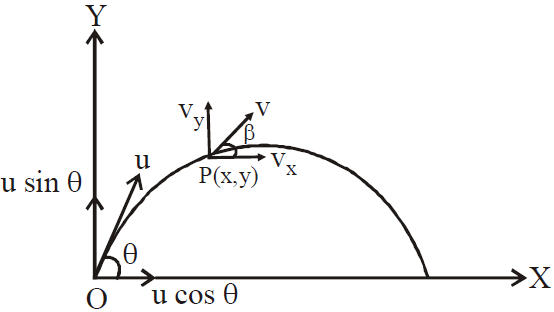
The components of the initial velocity in the X-direction and Y-direction are u cos θ and u sin θ respectively. Then at any instant of time t,
MOTION ALONG X-AXIS
ux = ucosθ, ax = 0
x = (u cosθ) t …(1)
MOTION ALONG Y-AXIS
uy = u sin θ, ay = –g
y = uyt +  ayt2
ayt2
y = u sinθ t + gt2 …(2)
gt2 …(2)
From equations (1) and (2) we get
y = x tanθ 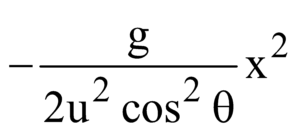 which is the equation of a parabola. Hence the path followed by the projectile is parabolic.
which is the equation of a parabola. Hence the path followed by the projectile is parabolic.
VELOCITY AT ANY POINT
Let vy be the vertical velocity of projectile at time t. (at P)
And vx be the horizontal component of velocity at time t.
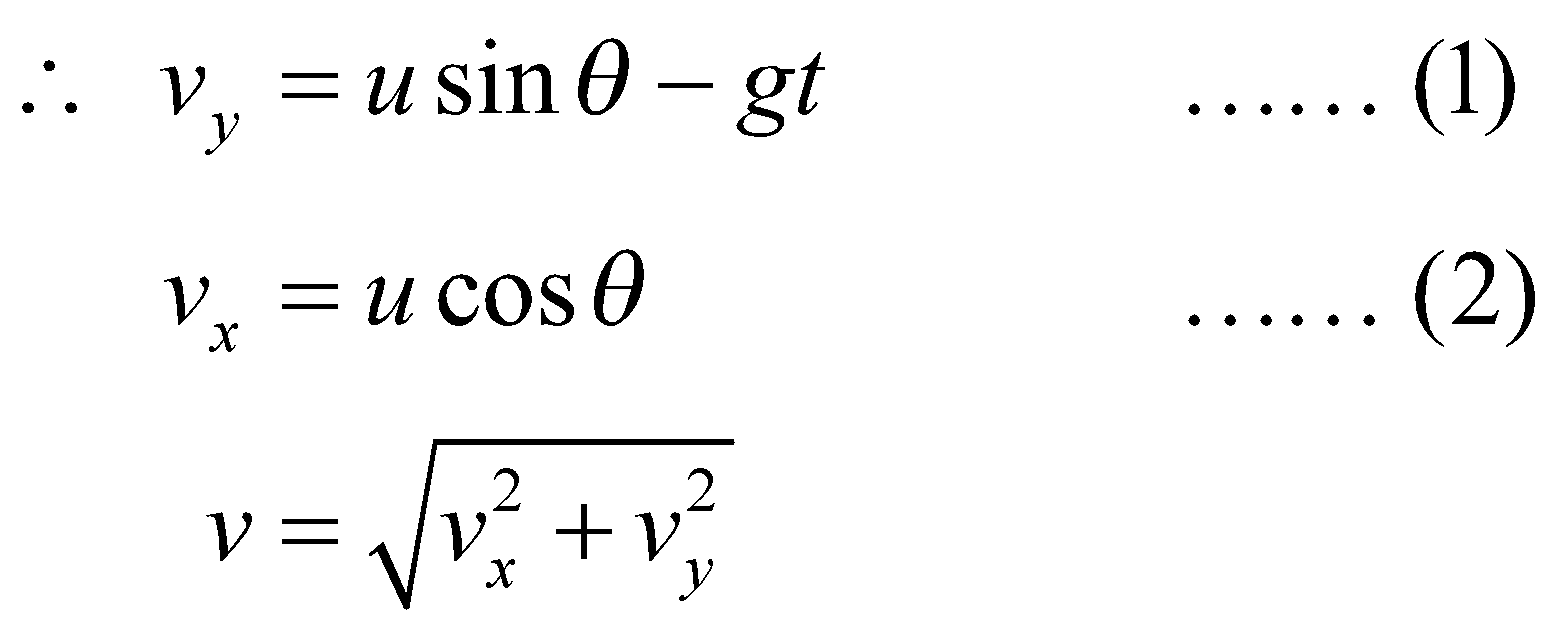
and the instantaneous angle (β) with horizontal is given by
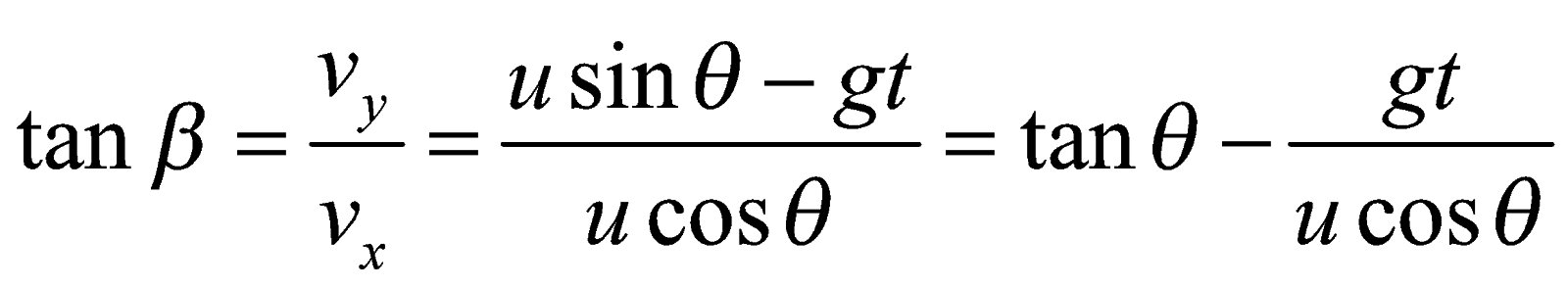
TIME OF FLIGHT
The time of flight of the projectile is given by
where ‘t’ is the time of ascent or descent.
MAXIMUM HEIGHT
Maximum height attained by the projectile is given by
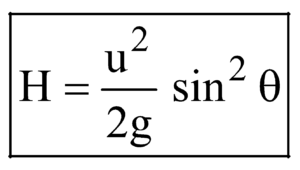 .
.In case of vertical motion, θ = 90º so maximum height attained
HORIZONTAL RANGE
The horizontal range of the projectile is given by
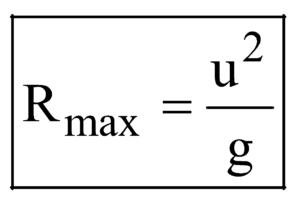 at θ = 45º (
at θ = 45º ( KEEP IN MEMORY
- The horizontal range of the projectile is same at two angles of projection for θ and (90° – θ).
- The height attained by the projectile above the ground is the largest when the angle of projection with the horizontal is 90° (vertically upward projection). In such a case time of flight is largest but the range is the smallest (zero).
- If the velocity of projection is doubled. The maximum height attained and the range become 4 times, but the time of flight is doubled.
- When the horizontal range of the projectile is maximum, (θ = 45°), then the maximum height attained is ¼th of the range.
- For a projectile fired from the ground, the maximum height is attained after covering a horizontal distance equal to half of the range.
The velocity of the projectile is minimum but not zero at the highest point, and is equal to u cosθ i.e. at the highest point of the trajectory, the projectile has net velocity in the horizontal direction (vertical component is zero). Horizontal component of velocity also remains same as the component of g in horizontal direction is zero i.e., no acceleration in horizontal direction.
PROJECTILE ON AN INCLINED PLANE
Let a body is thrown from a plane OA inclined at an angle α with the horizontal, with a constant velocity u in a direction making an angle θ with the horizontal.
The body returns back on the same plane OA.
Hence the net displacement of the particle in a direction normal to the plane OA is zero.
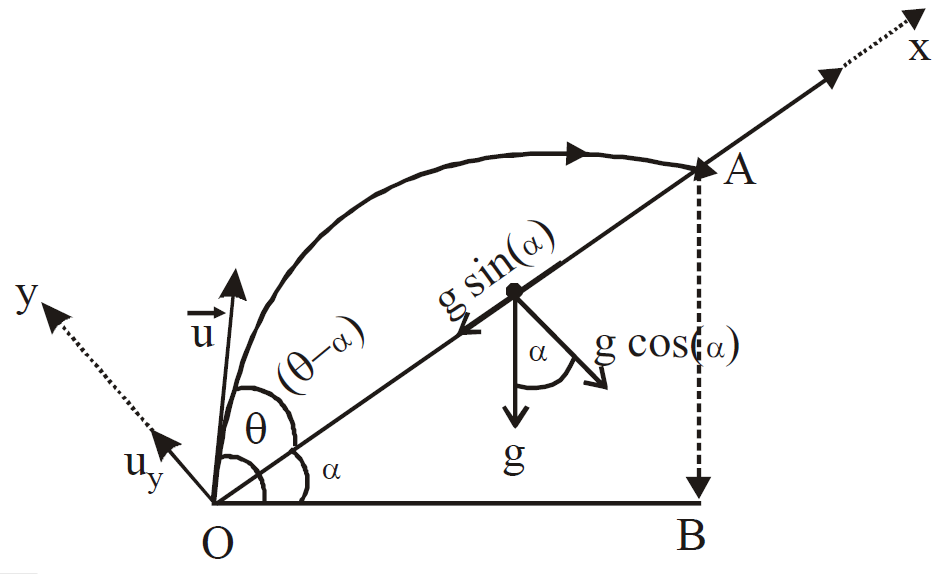
ux = u cos (θ –α) along the incline, + x-axis)
uy = u sin (θ –α) along the incline, + y-axis)
ax = g sin α along – x-axis, as retardation
ay = g cos α along – y-axis, as retardation
The time of flight of the projectile is given by
or 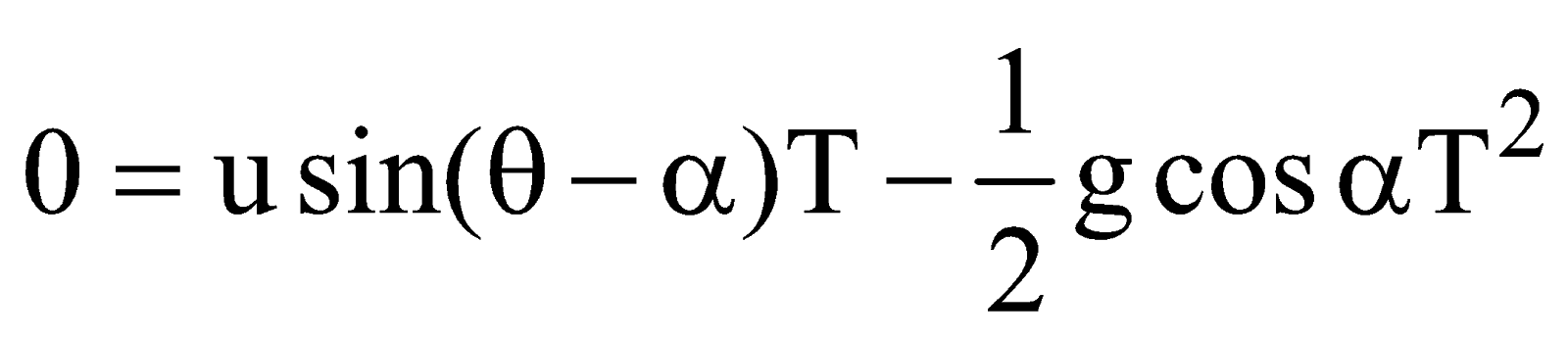
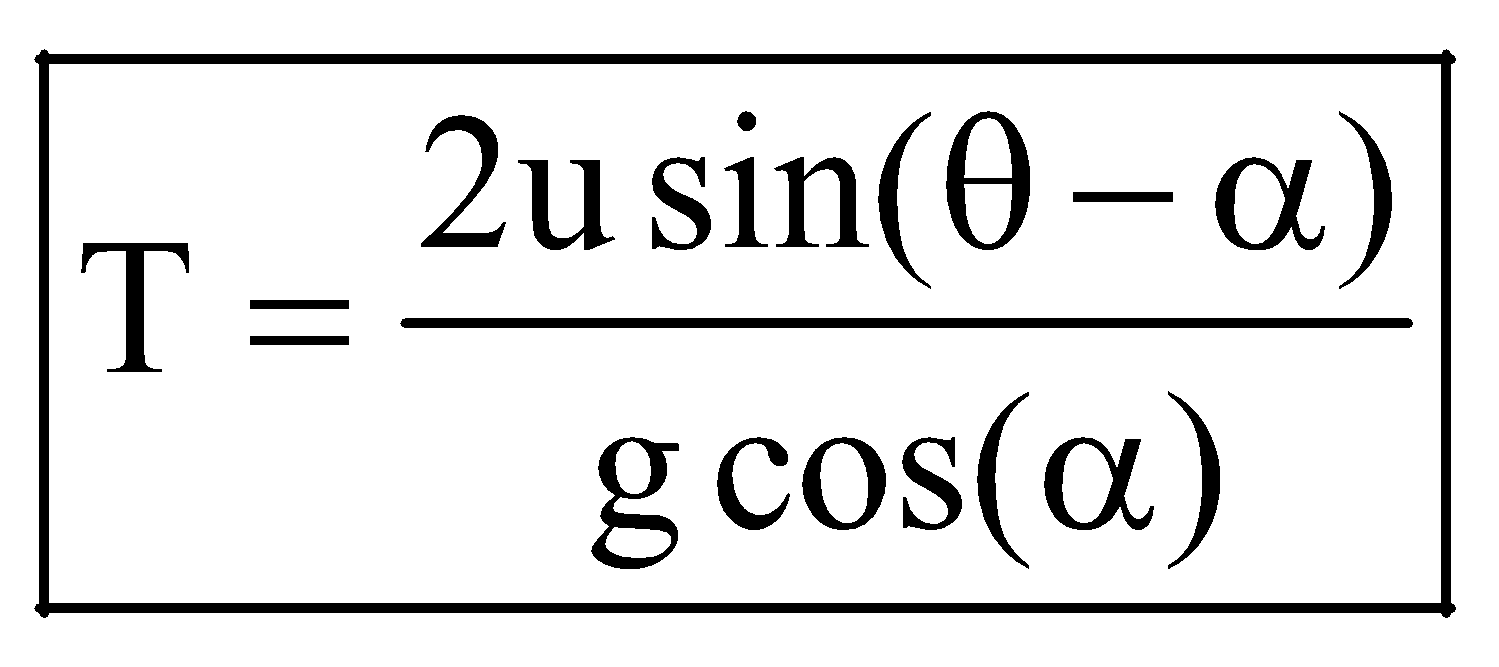
If maximum height above the inclined plane is H,
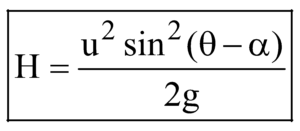
The horizontal range R of the projectile is given by
OB = u cos θ t = 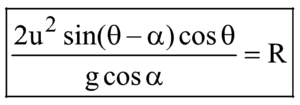
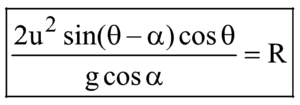
The range of the projectile at the inclined plane is given by
OA = 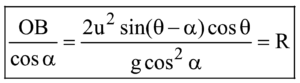
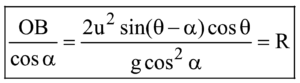
CONDITION FOR HORIZONTAL RANGE (R) ON THE INCLINED PLANE TO BE MAXIMUM
Since 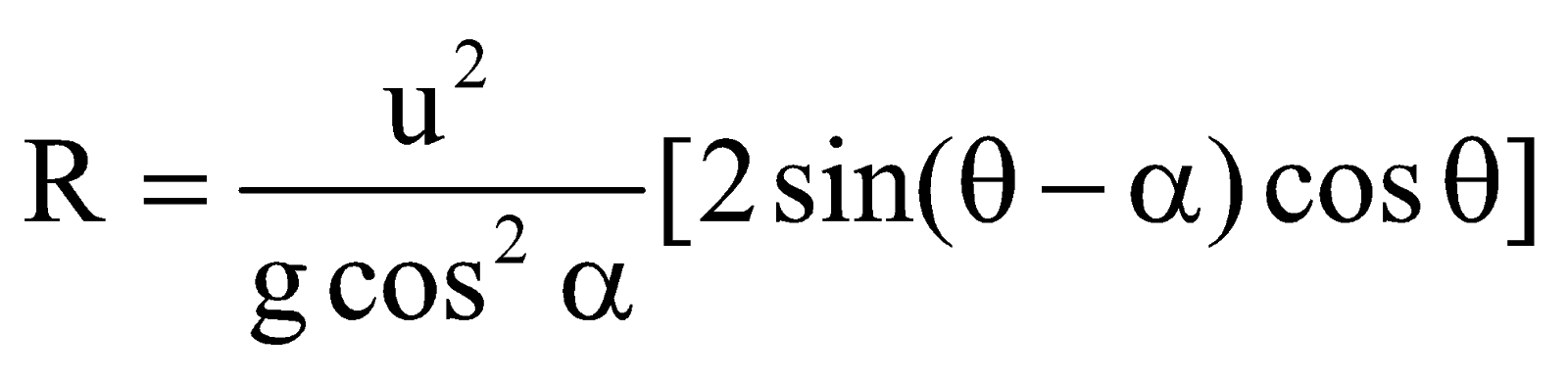
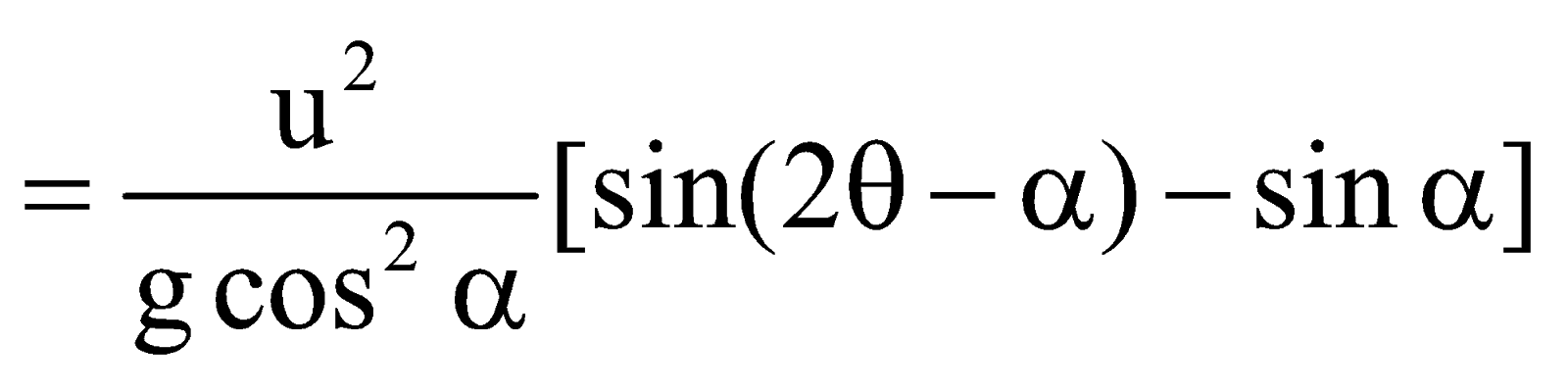
{2 sin A cos B = sin(A+B)+sin(A–B)}
R is maximum when sin (2θ –α) is maximum
i.e., sin (2θ – α) = 1 or 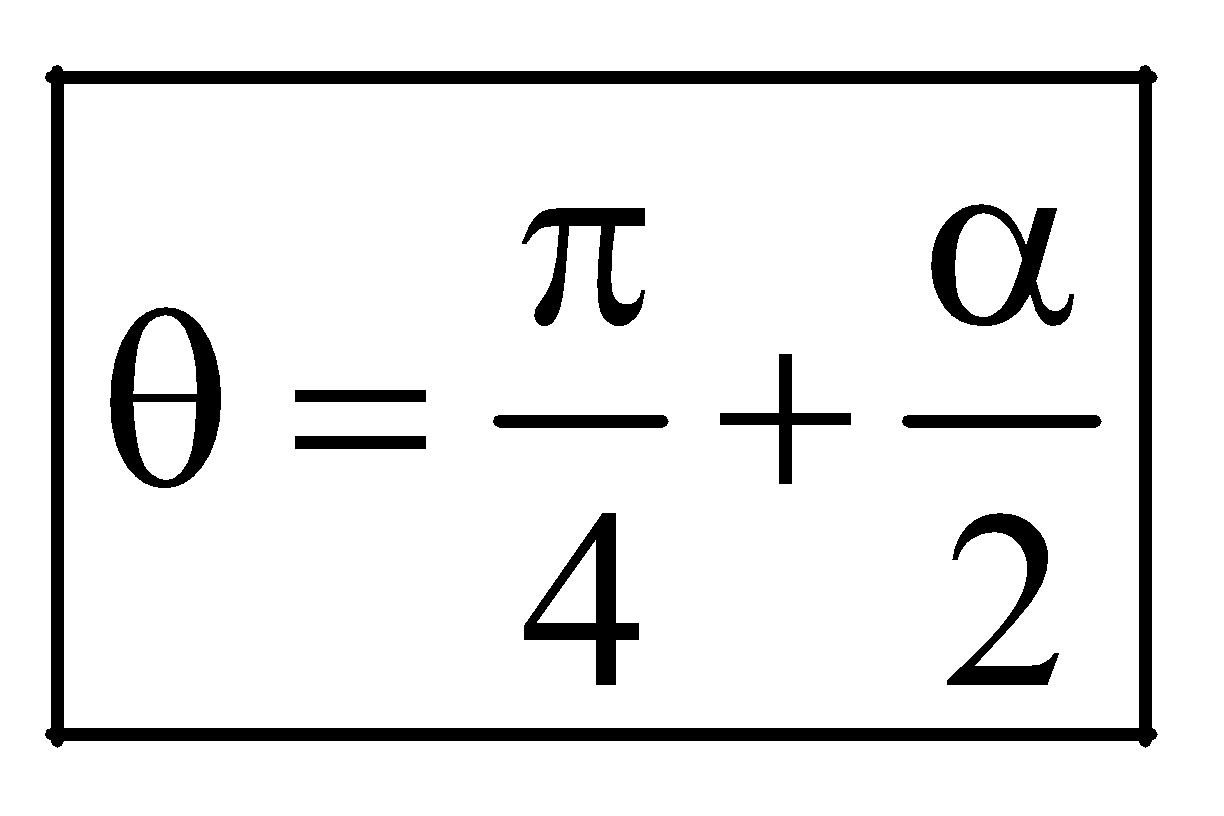
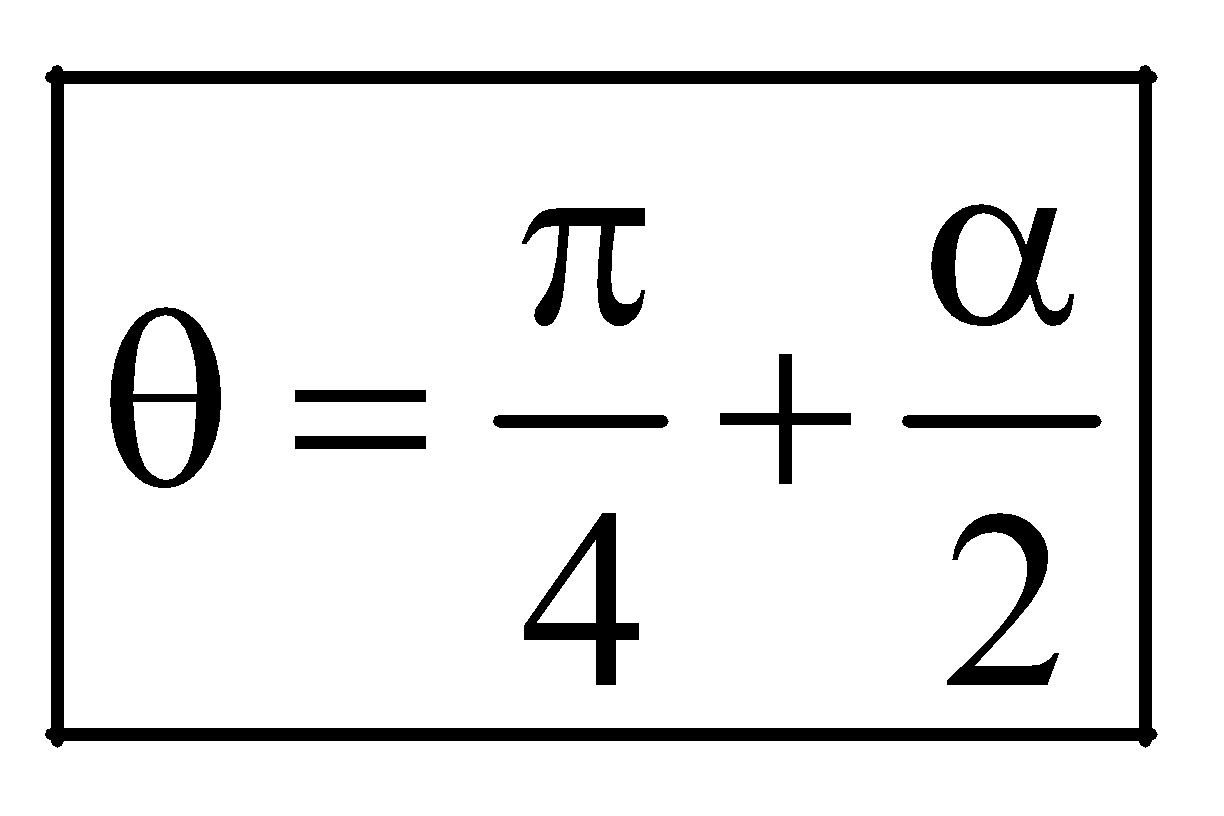
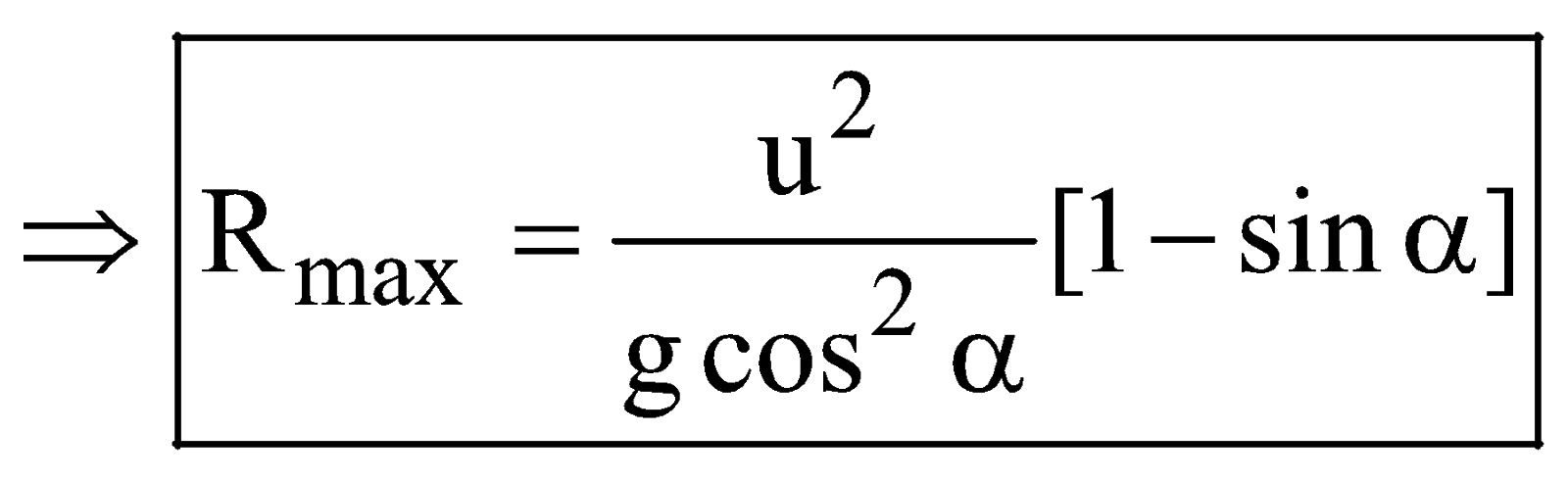
or Rmax(on inclined plane) 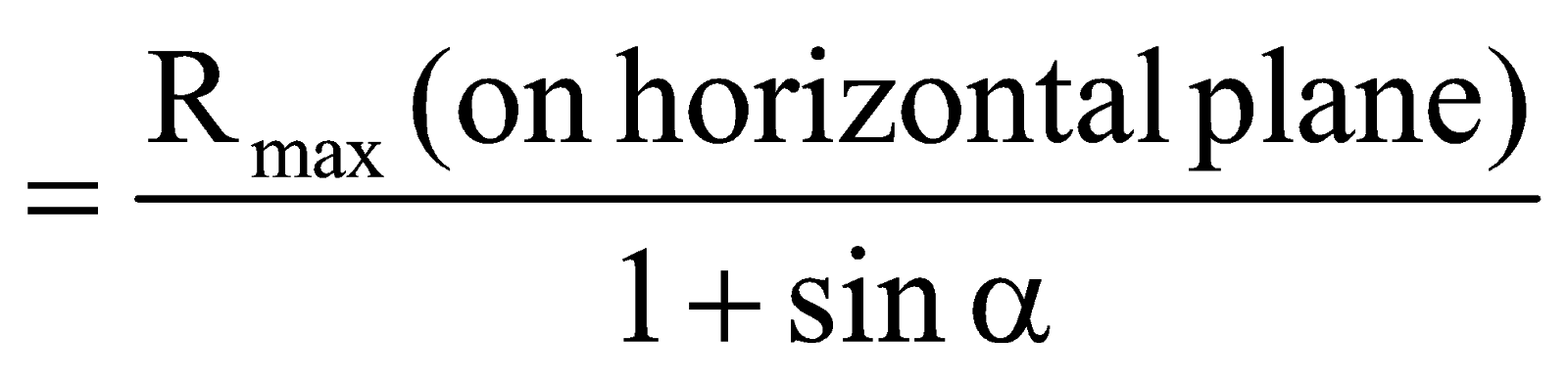
where Rmax (on horizontal plane) 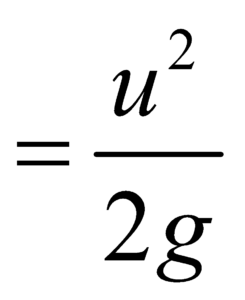 .
.
CONDITION FOR TIME OF FLIGHT (T) TO BE MAXIMUM
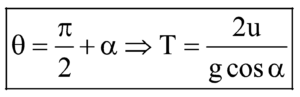
It means that if θ1 is the angle for projectile for which T is maximum and θ2 is the angle for which R is maximum, then θ1 = 2θ2.
KEEP IN MEMORY
- Equation of trajectory of an oblique projectile in terms of range (R) is
- There are two unique times at which the projectile is at the same height h(< H) and the sum of these two times.
Since, h = (u sin θ)t 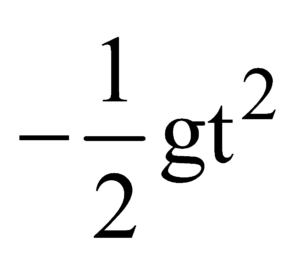 is a quadratic in time, so it has two unique roots t1 and t2 (say) such that sum of roots
is a quadratic in time, so it has two unique roots t1 and t2 (say) such that sum of roots
(t1 + t2) is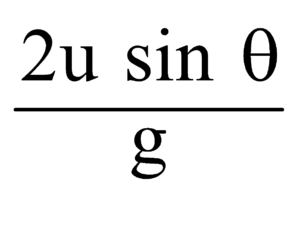 and product (t1t2) is
and product (t1t2) is  .
.
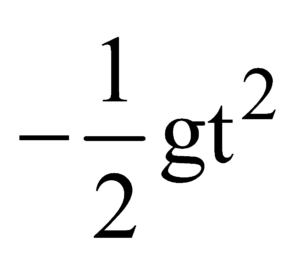 is a quadratic in time, so it has two unique roots t1 and t2 (say) such that sum of roots
is a quadratic in time, so it has two unique roots t1 and t2 (say) such that sum of roots (t1 + t2) is
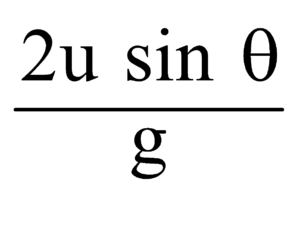 and product (t1t2) is
and product (t1t2) is The time lapse (t1– t2) is 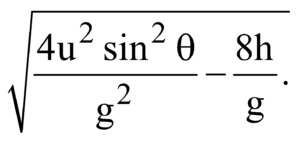
UNIFORM AND NON-UNIFORM CIRCULAR MOTION
UNIFORM CIRCULAR MOTION
An object moving in a circle with a constant speed is said to be in uniform circular motion. Example – Motion of the tip of the second hand of a clock.
ANGULAR DISPLACEMENT : Change in angular position is called angular displacement (dθ).
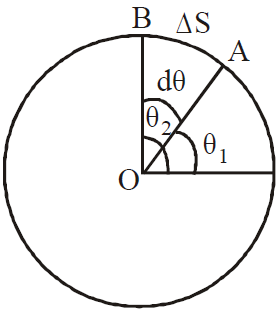
ANGULAR VELOCITY : Rate of change of angular displacement is called angular velocity ω
i.e., 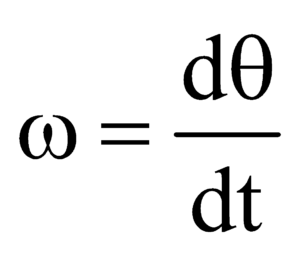
Relation between linear velocity (v) and angular velocity (ω).
ANGULAR ACCELERATION : Rate of change of angular velocity is called angular acceleration.
i.e., 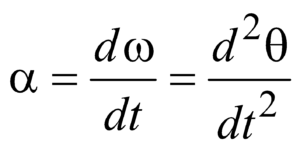
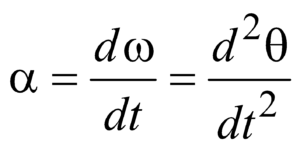
Relation between linear acceleration and angular acceleration.

CENTRIPETAL ACCELERATION : Acceleration acting on a body moving in uniform circular motion is called centripetal acceleration. It arises due to the change in the direction of the velocity vector.
Magnitude of centripetal acceleration is
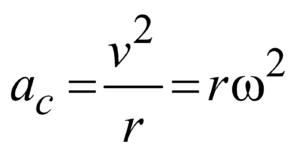
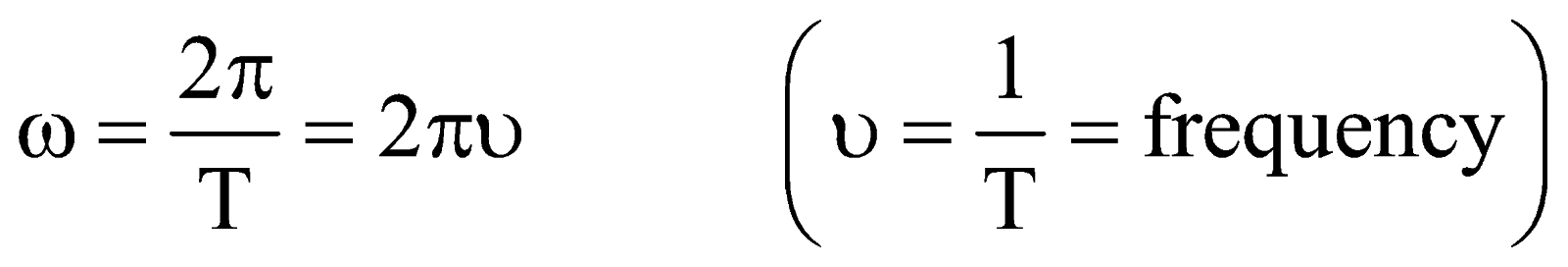
This acceleration is always directed radially towards the centre of the circle.
CENTRIPETAL FORCE : The force required to keep a body moving in uniform circular motion is called centripetal force.
It is always directed radially inwards.
CENTRIFUGAL FORCE : Centrifugal force is a fictitious force which acts on a body in rotating (non-inertial frames) frame of reference.
Magnitude of the centrifugal force 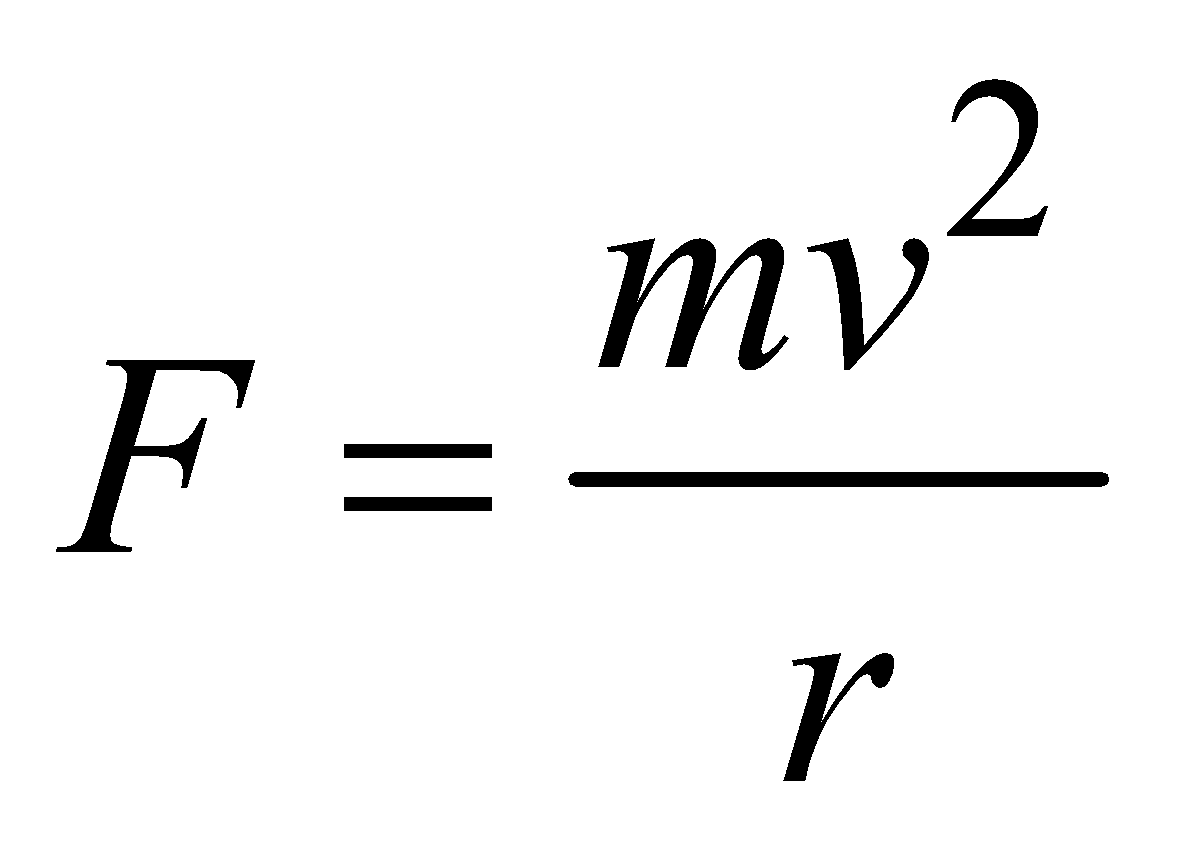
This force is always directed radially outwards and is also called coriolis force.
NON-UNIFORM CIRCULAR MOTION
An object moving in a circle with variable speed is said to be in non-uniform circular motion.
If the angular velocity varies with time, the object has two accelerations possessed by it, centripetal acceleration (ac) and Tangential acceleration (aT) and both perpendicular to each other.
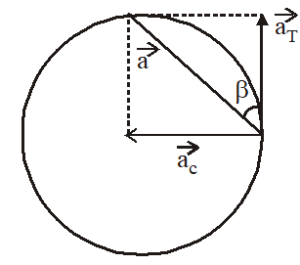
Net acceleration
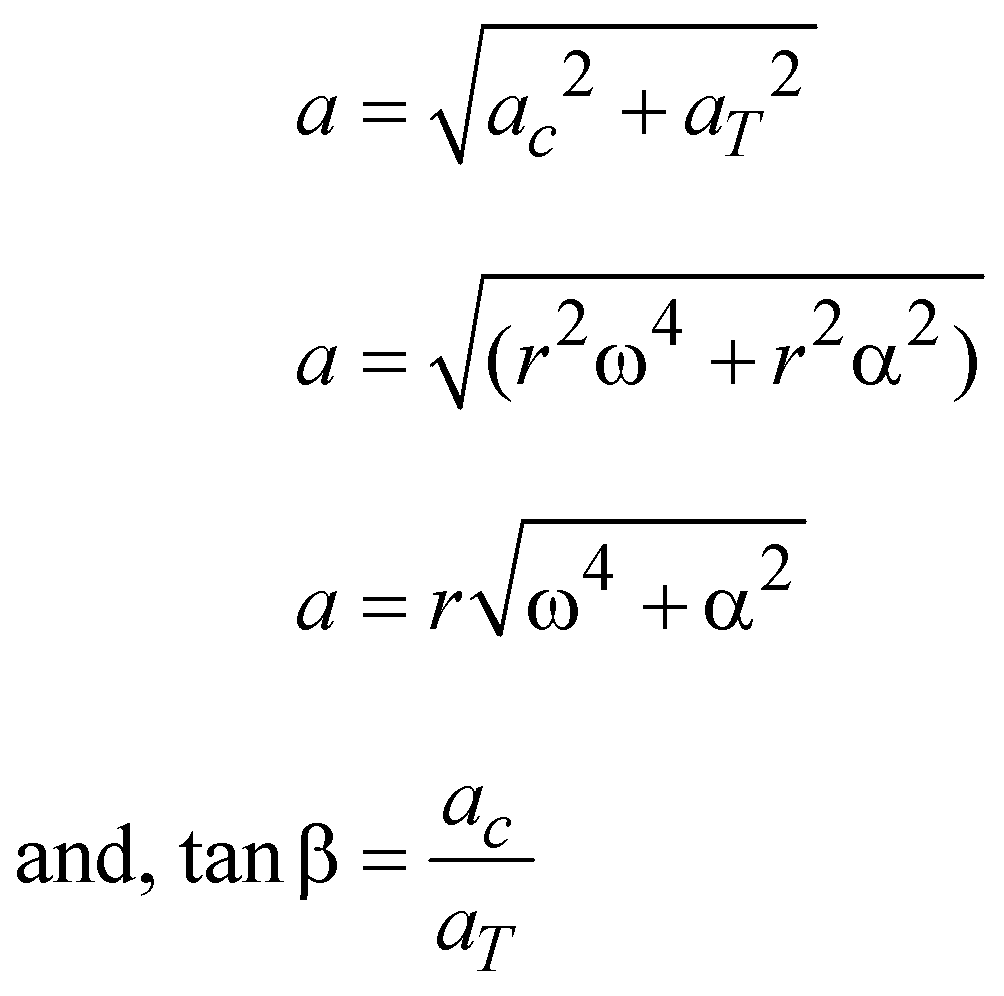
KEEP IN MEMORY
- Angular displacement behaves like vector, when its magnitude is very small. It follows laws of vector addition.
- Angular velocity and angular acceleration are axial vectors.
- Centripetal acceleration always directed towards the centre of the circular path and is always perpendicular to the instantaneous velocity of the particle.
- Circular motion is uniform if aT = rα = 0, that is angular velocity remains constant and radial acceleration
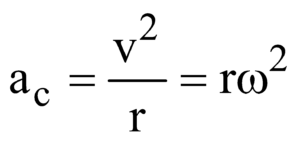 is constant.
is constant. - When aT or α is present, angular velocity varies with time and net acceleration is
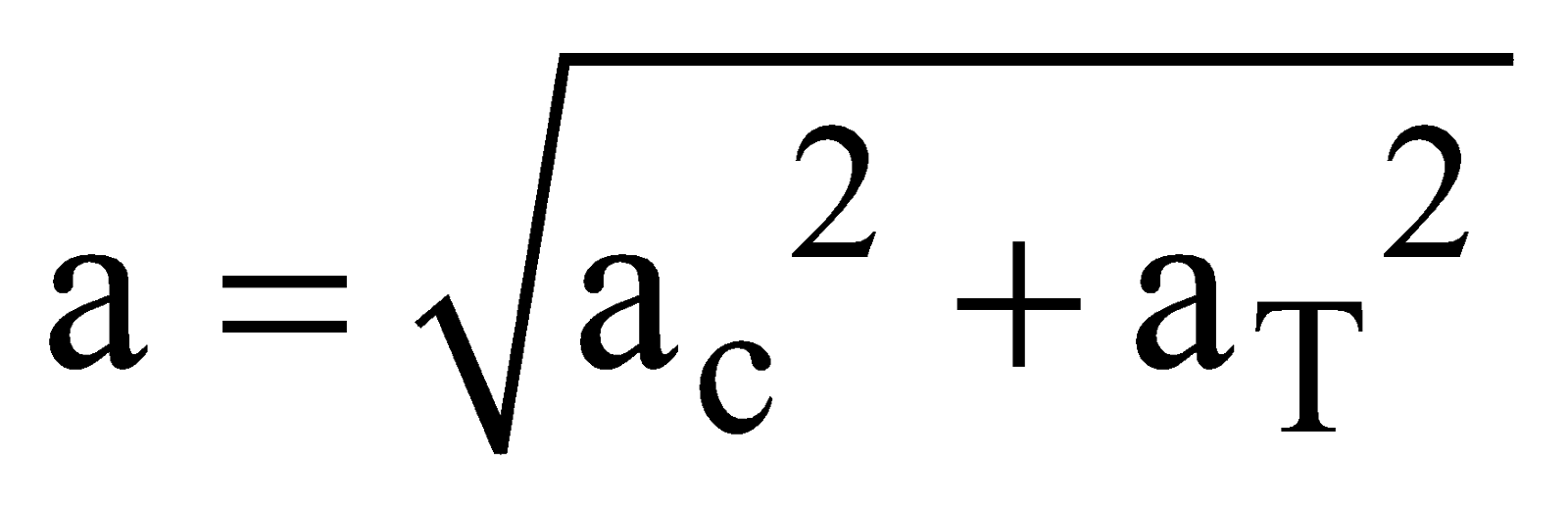
- If aT = 0 or α = 0, no work is done in circular motion.
