9.1 Simple harmonic motion
Understanding
➔ The defining equation of SHM
➔ Energy changes
Applications and skills
➔ Solving problems involving acceleration, velocity and displacement during simple harmonic motion, both graphically and algebraically
➔ Describing the interchange of kinetic and potential energy during simple harmonic motion
➔ Solving problems involving energy transfer during simple harmonic motion, both graphically and algebraically
Equations
➔ angular velocity–period equation: ω =2π/T
➔ defining equation for shm: a = -ω2x
➔ displacement–time equations: x = x0 sin ωt; x = x0 cos ωt
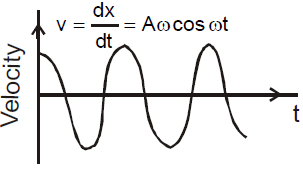
➔ velocity–time equations: v = ωx0 cos ωt; v = -ωx0 sin ωt
➔ velocity-displacement equation: v = ±ω √( x02 – x2 )
➔ kinetic energy equation: Ek =1/2 mω2( x02 – x2 )
➔ total energy equation: E = 1/2 mω2x02
➔ period of simple pendulum: T = 2π√ (l /g)
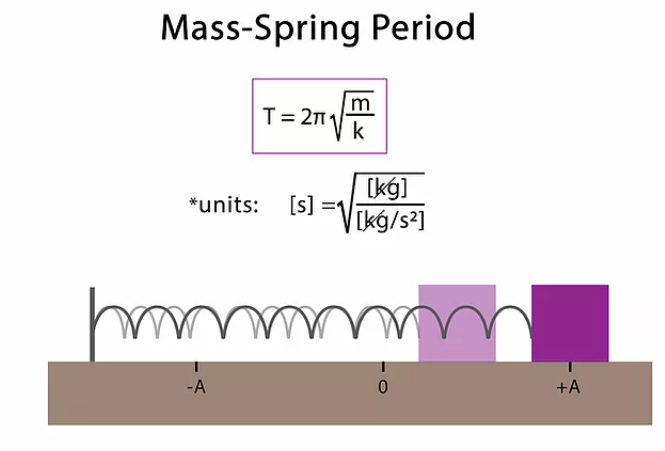
➔ period of mass–spring: T = 2π√ (m/k)
9.1 Simple Harmonic Motion (SHM)
Period of the motion is related to the angular frequency (ω), not to the amplitude or to the phase. T = 2π/ω.
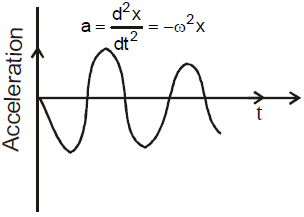
Acceleration is proportional and in the opposite direction to the displacement. a = –ω²x.
Spring
Restoring force: After being moved a distance A (Amplitude) from equilibrium point, there will be a restoring force towards the center.
When there are two springs, the force doubles!
Period is independent of the amplitude/extension.
Simple pendulum
Small angle approximation: Acceleration is not proportional to the displacement (x). But if x is small (x < 10º) then sin(x/L) is approximately equal to x/L.
Period is independent of the mass.
Formulas
When at t = 0, the displacement equals the amplitude:
x = xo cos(ωt);
v = -ωxo sin(ωt);
a = -ω²xo cos(ωt) = -ω²x.
When at t = 0, the displacement (x) equals zero:
x = xo sin(ωt);
v = -ωxo cos(ωt);
a = -ω²xo sin(ωt) = -ω²x.
Maximums: The maximum speed is ωxo and maximum acceleration is ω²xo.
Circular motion and SHM
Energy in SHM systems
Total energy conservation: ET = EK + EP.
ET = 1/2 mω²xo².
EK = 1/2 mv² = 1/2 mω² xo² sin²(ωt) = 1/2 mω² (xo² – x²).
EP = 1/2 mω² xo² cos²(ωt) = 1/2 mω²x².
PERIODIC AND OSCILLATORY MOTION
PERIODIC MOTION
When a body repeats its motion after regular interval of time, it is said to be in periodic motion. The path of periodic motion may be rectilinear, open/closed curvilinear. Example:
- Motion of moon around earth
- Motion of a piston in a cylinder
- Motion of a simple pendulum etc.
OSCILLATORY MOTION
If during a periodic motion, the particle moves to and fro on the same path, the motion is vibratory or oscillatory.Example :
- The motion of a ball in bowl
- The needle of a sewing machine
- Vibrations of prongs of tuning fork etc.
Note:-
- All oscillatory motion are periodic but all periodic motion are not oscillatory motion.
- The oscillatory motion which can be expressed in terms of sine and cosine function, is said to be harmonic motion.
SIMPLE HARMONIC MOTION (S.H.M.)
If a particle moves up and down (back and forth) about a mean position (also called equilibrium position) in such a way that a restoring force/ torque acts on particle, which is proportional to displacement from mean position, but in opposite direction from displacement, then motion of the particle is called simple harmonic motion. If displacement is linear, it is called linear S.H.M. and if displacement is angular, it is called an angular S.H.M.Example :
- Motion of a body suspended by a spring
- Oscillations of simple pendulum
EQUATIONS OF S.H.M.
LINEAR S.H.M.The restoring force is proportional to the displacement from mean position.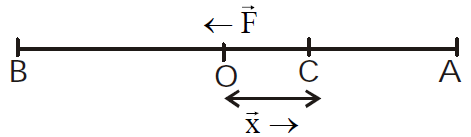 i.e., F ∝ – xor,
i.e., F ∝ – xor, ![]() where k is called force constant or spring constantor,
where k is called force constant or spring constantor, ![]()
ANGULAR S.H.M.The restoring torque is proportional to the angular displacement from the mean position.![]() where C is called torsional rigidityor,
where C is called torsional rigidityor, ![]() or,
or, ![]()
TERMS RELATED TO S.H.M.
- Amplitude : The maximum displacement of the oscillating particle on either side of its mean position is called its amplitude. It is denoted by A.
- Time period : The time taken by a oscillating particle to complete one oscillation is called its time period. It is denoted by T.
- Frequency : It is the number of oscillations completed in one second.
It is denoted by υ.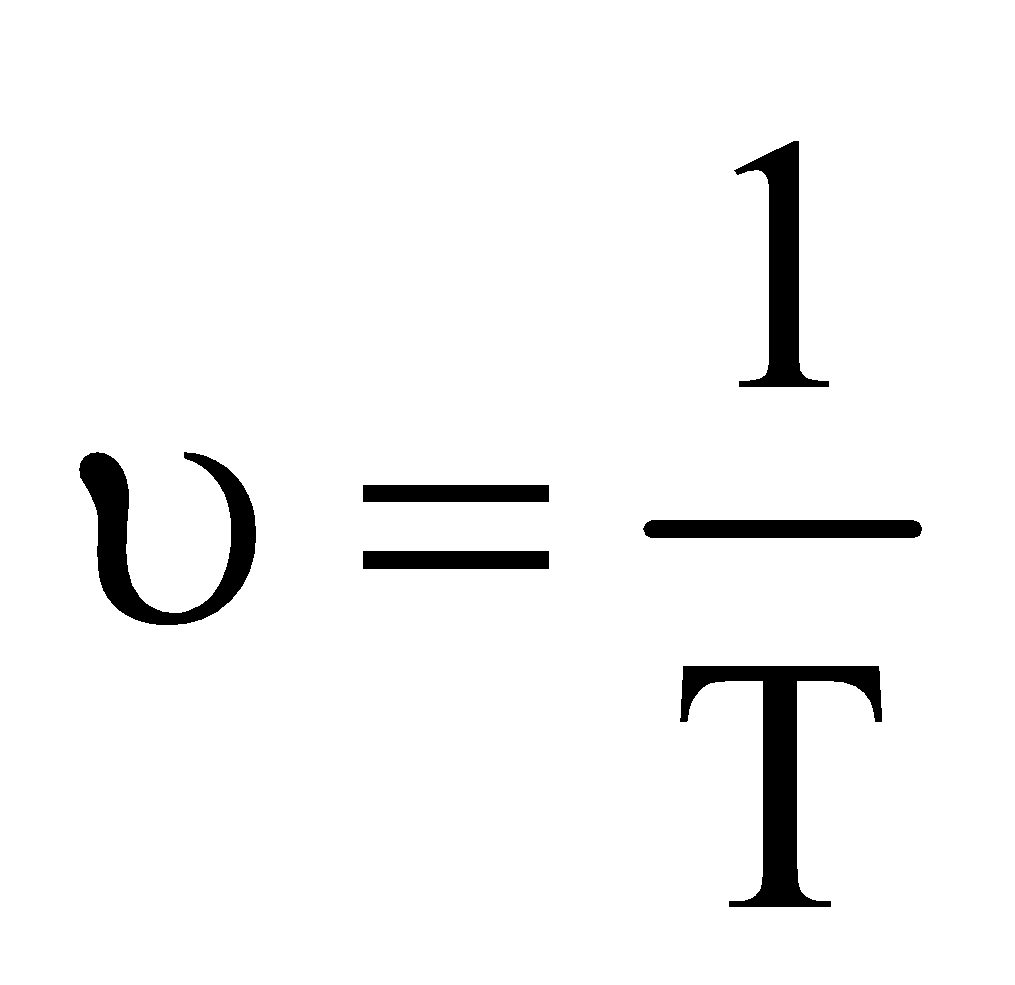
The S.I. unit of frequency is s–1 or Hz.
- Angular frequency
![]() The S.I. unit of angular frequency is rad/sec.
The S.I. unit of angular frequency is rad/sec.
- Phase : The parameter, by which the position of particle from its mean position is represented, is known as phase. The phase at any instant tells the state of position & direction of motion at that instant. The phase at time t = 0 is known as the initial phase or epoch (e).
- Total phase angle : The total angle (ωt + θ) is known as total phase angle.
CHARACTERISTICS OF S.H.M.
DISPLACEMENT
The displacement of a particle in S.H.M. is given by![]() where A is amplitude, ω is angular frequency and (ωt + φ) is called the phase of the particle at any instant t.
where A is amplitude, ω is angular frequency and (ωt + φ) is called the phase of the particle at any instant t.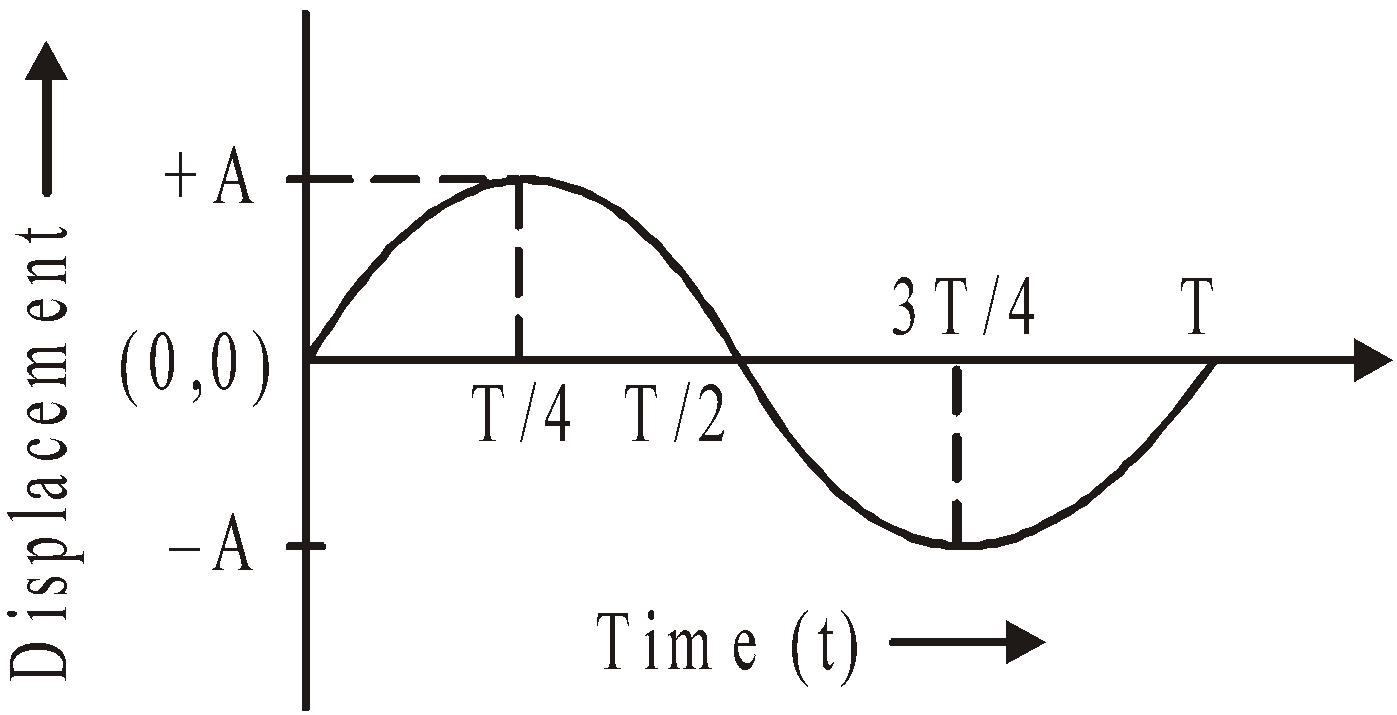
VELOCITY
The velocity of a particle in S.H.M. is given by![]() or,
or, ![]() At y = 0 (at mean position),
At y = 0 (at mean position), ![]()
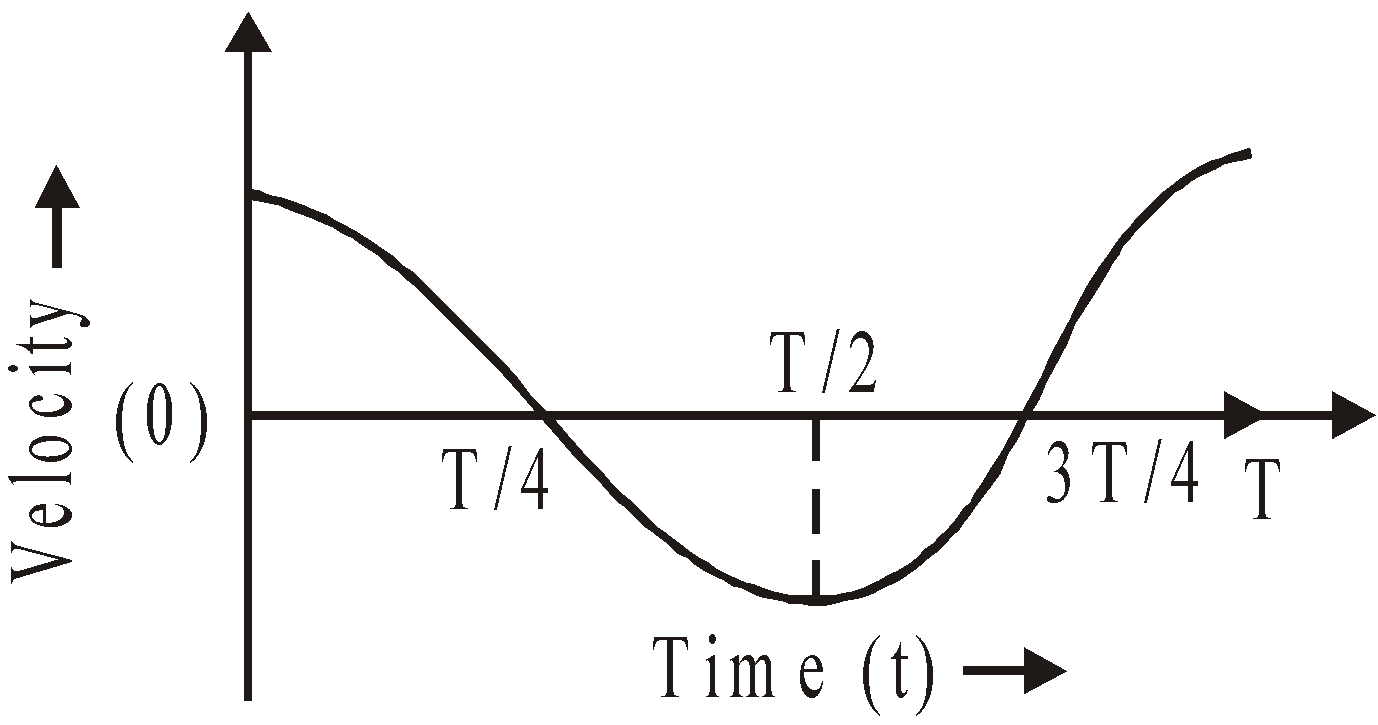
ACCELERATION : The acceleration of a particle in S.H.M. is given by![]() or a = – ω2yThe negative sign indicates that the acceleration is directed towards the mean positionAt y = A (at extreme position), amax = – ω2A
or a = – ω2yThe negative sign indicates that the acceleration is directed towards the mean positionAt y = A (at extreme position), amax = – ω2A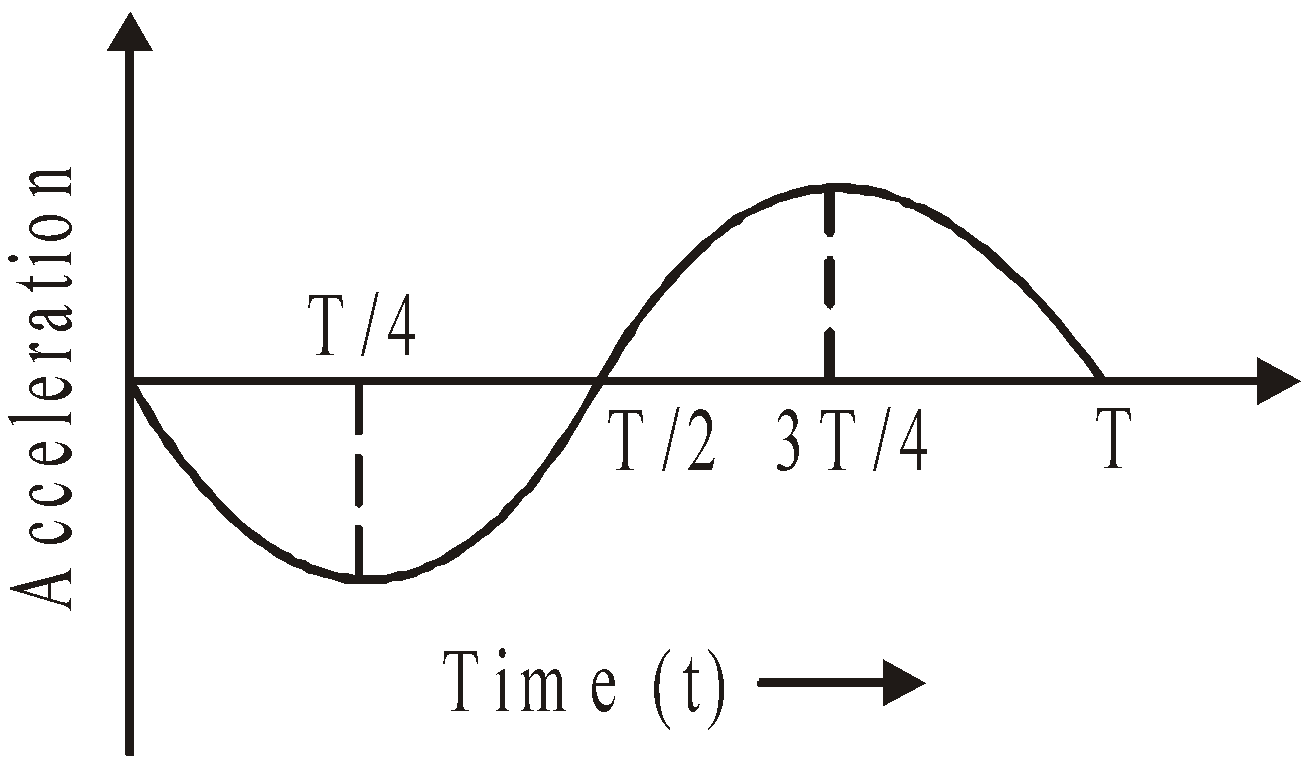
ENERGY
- Kinetic energy : A particle in S.H.M. possesses kinetic energy by virtue of its motion.
![]()
- Potential energy : A particle in S.H.M. possesses potential energy due to its displacement from the mean position.
![]()
- Total mechanical energy
E = K.E. + P.E.![]()
![]()
![]()
The curves representing KE, PE and total energy are shown in figure.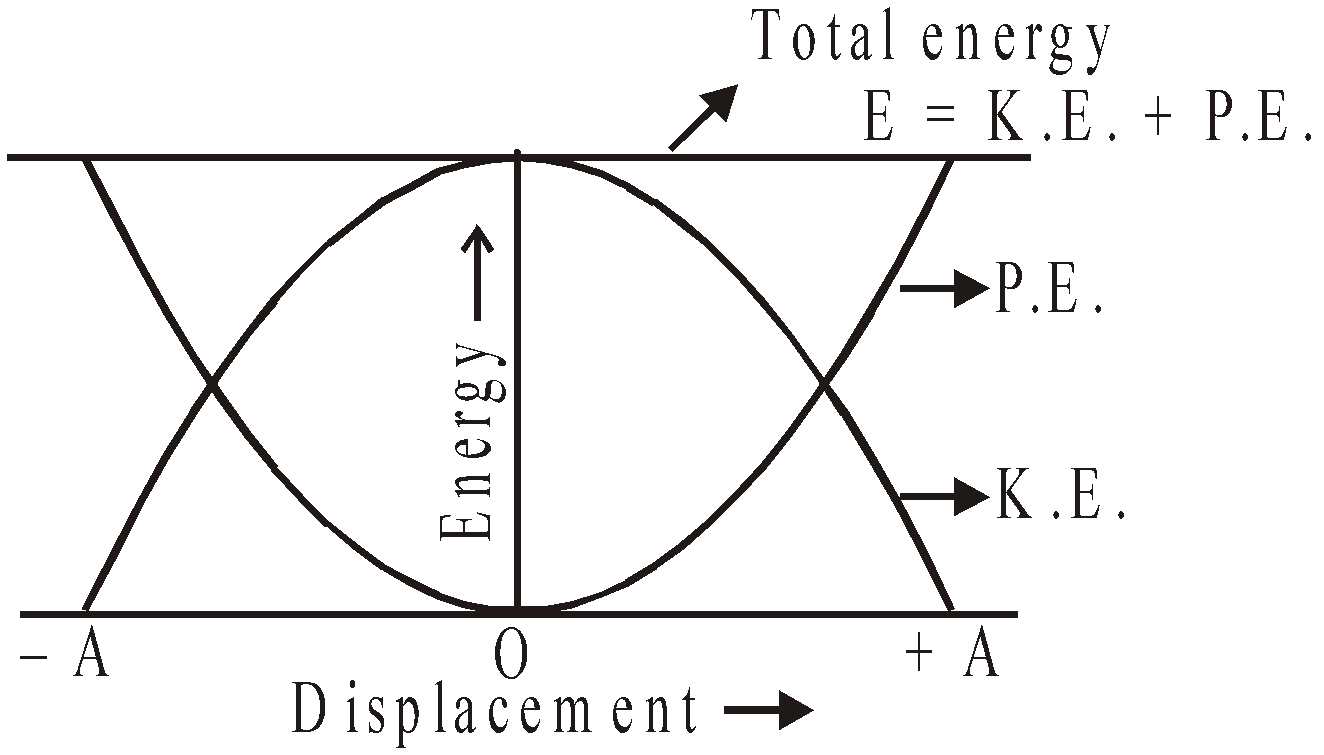
KEEP IN MEMORY
- Restoring force F = – Mω2x
- Kinetic energy = (1/2) Mω2(A2 – x2)
- Potential energy = 1/2 Mω2×2
- Total energy of SHM = 1/2 Mω2A2
Equation a = – ω2y shows that if body perform S.H.M. then acceleration of the body is proportional to displacement, but in the opposite direction of displacement. It is an essential requirement for any motion to be S.H.M.
- The kinetic and potential energy of SHM varies sinusoidally with a frequency twice that of SHM.
- Total energy

where n = frequency of vibration.
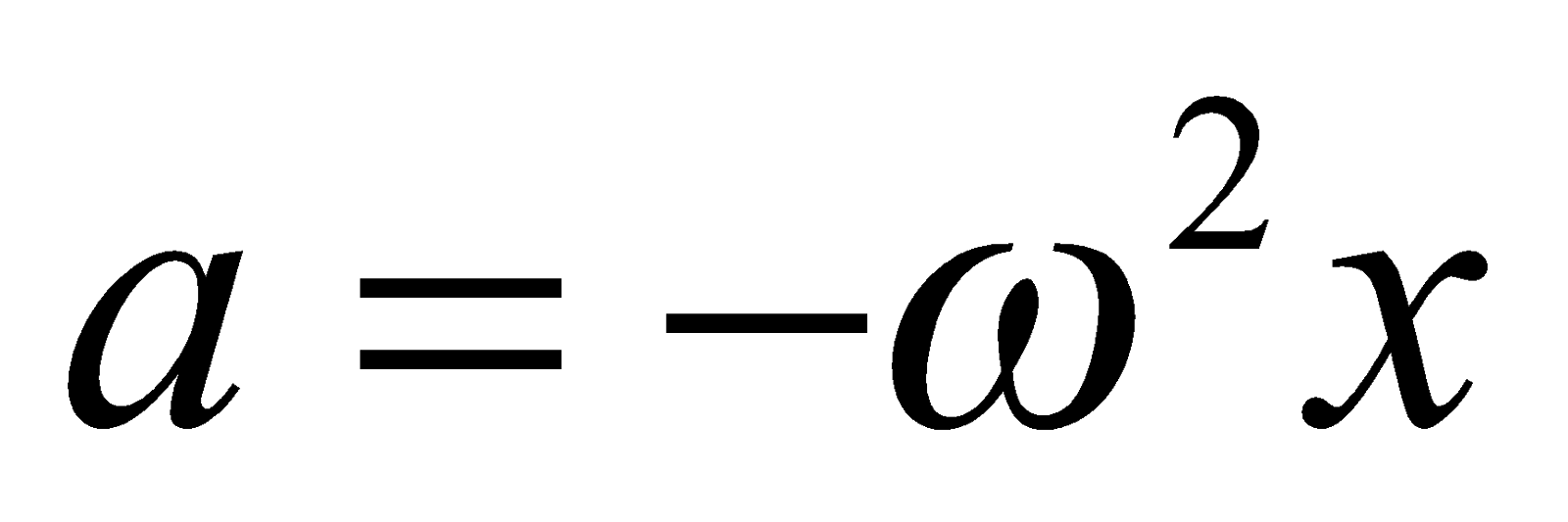 where ω is constant
where ω is constant 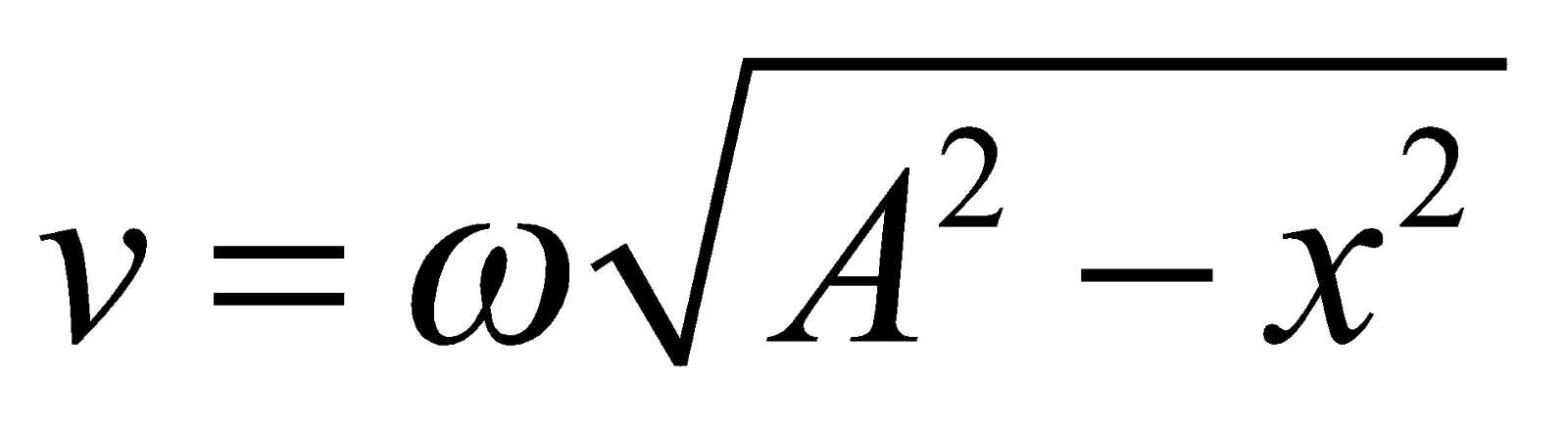

- Geometrically the projection of the body undergoing uniform circular motion on the diameter of the circle is SHM.
- In a non-inertial frame.
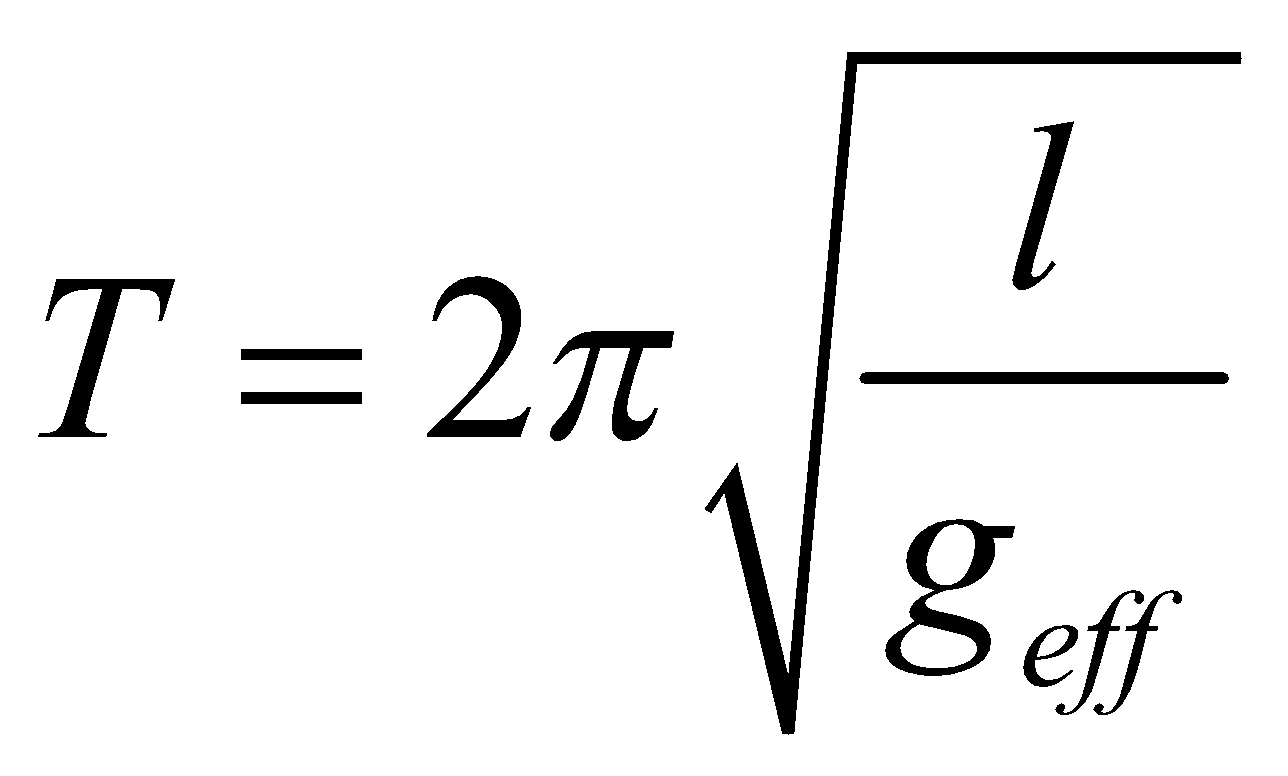

SOME SYSTEMS EXECUTING S.H.M.
CASE 1 – Spring mass system
- When two springs having force constants k1 and k2 connected in parallel, then
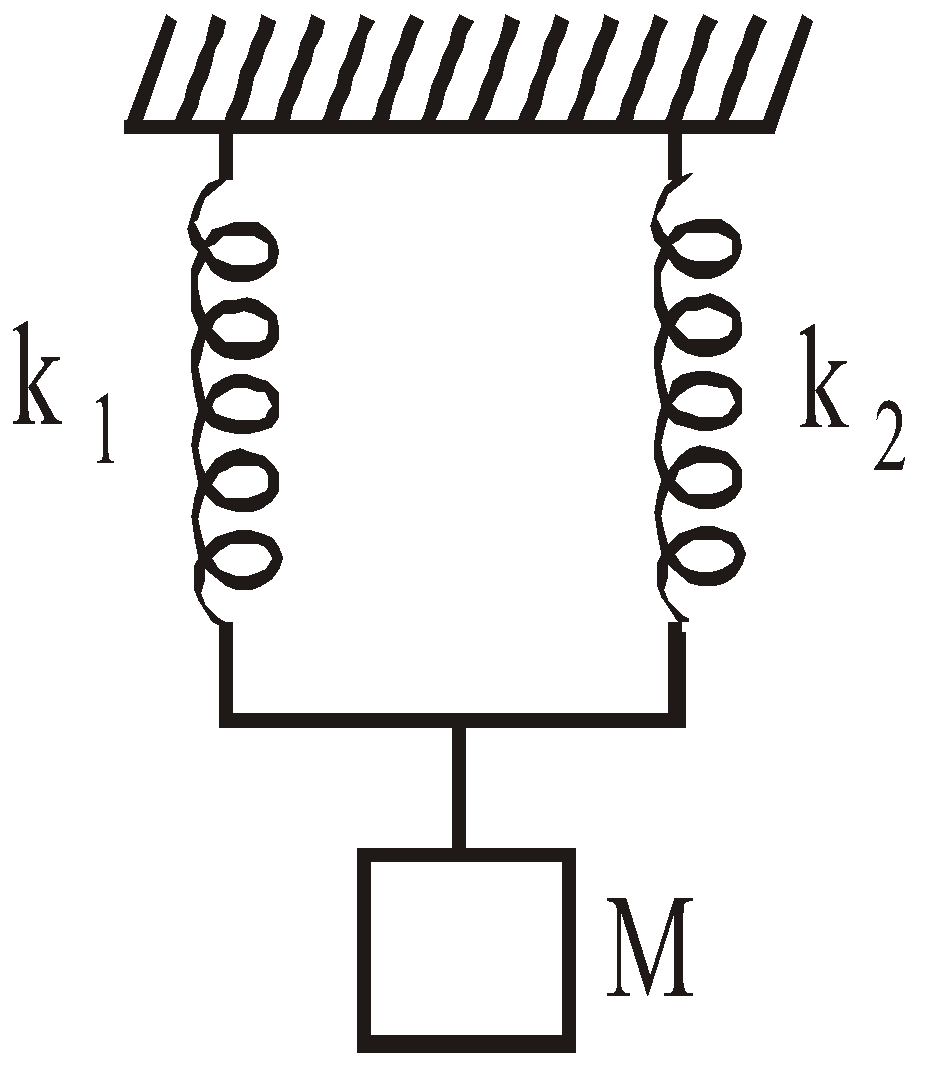 The force constant of the combination is k = k1 + k2 and hence T = 2π[M/(k1 + k2)]1/2
The force constant of the combination is k = k1 + k2 and hence T = 2π[M/(k1 + k2)]1/2
- When two springs of force constants k1 and k2 are connected in series, then
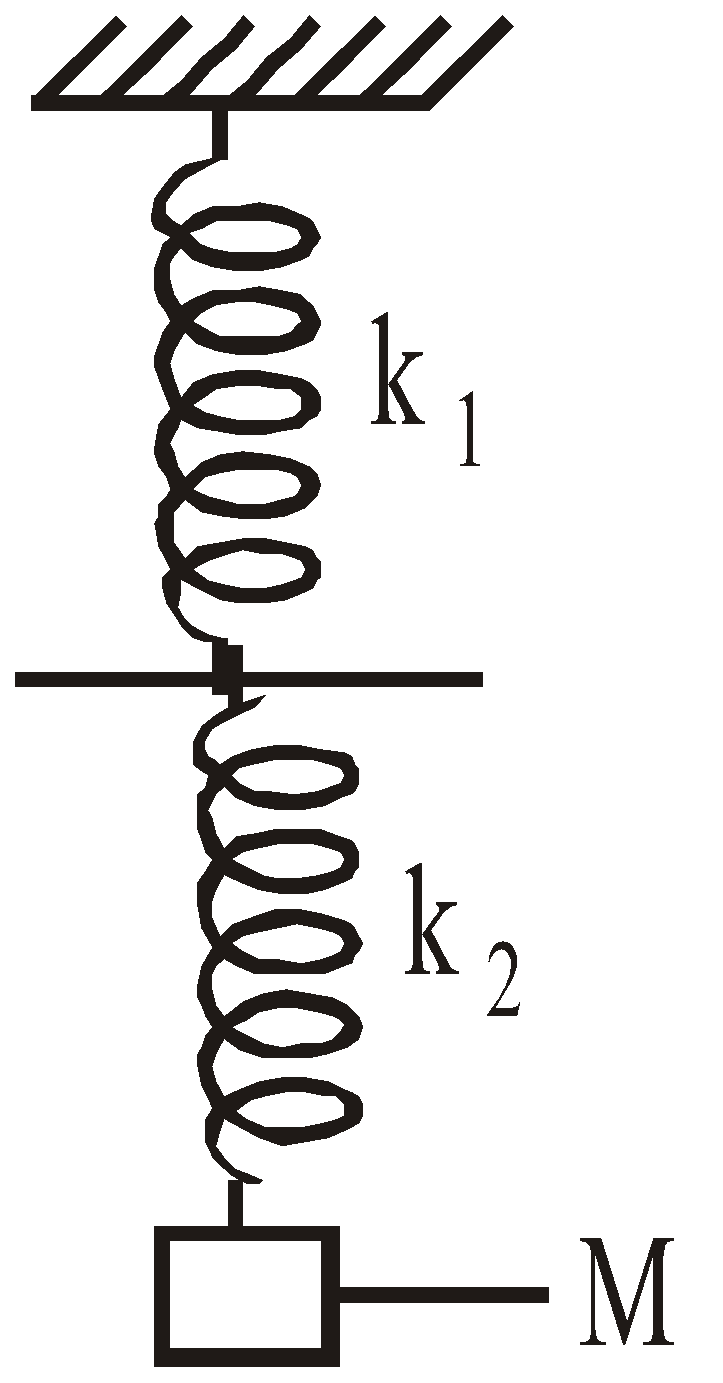 The force constant of the combination is 1/k = 1/k1 + 1/k2. i.e., k = k1k2/(k1 + k2) Hence
The force constant of the combination is 1/k = 1/k1 + 1/k2. i.e., k = k1k2/(k1 + k2) Hence ![]()
- If two mass M1 and M2 are connected at the two ends of the spring, then their period of oscillation is given by
![]() T = 2π[μ/k)]1/2 where
T = 2π[μ/k)]1/2 where ![]() is the reduced mass.
is the reduced mass.
- When the length of spring increases, spring constant decreases. If the length of spring becomes n times, its spring constant becomes
 times and therefore time period will be increased by
times and therefore time period will be increased by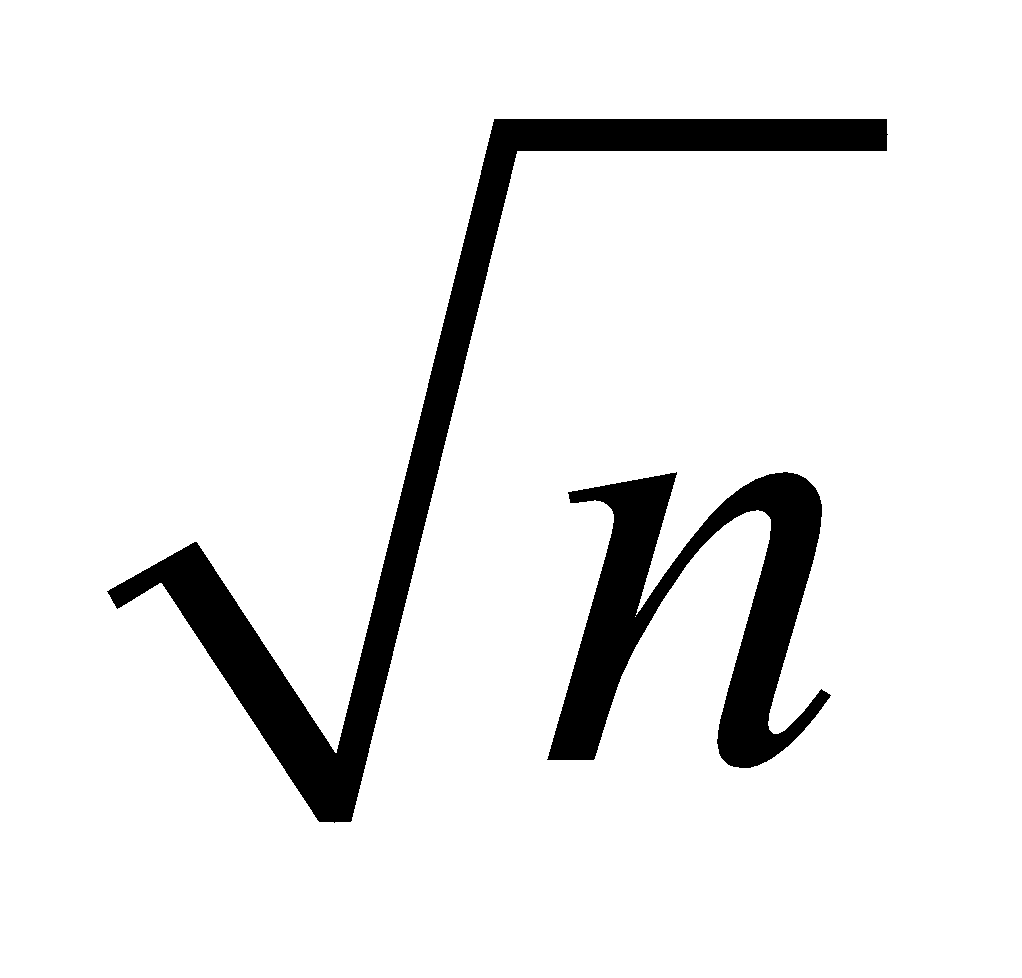 times.
times. - If we divide the spring into n equal parts, the spring constant of each part becomes n k. Hence time period when the same mass is suspended from each part is:
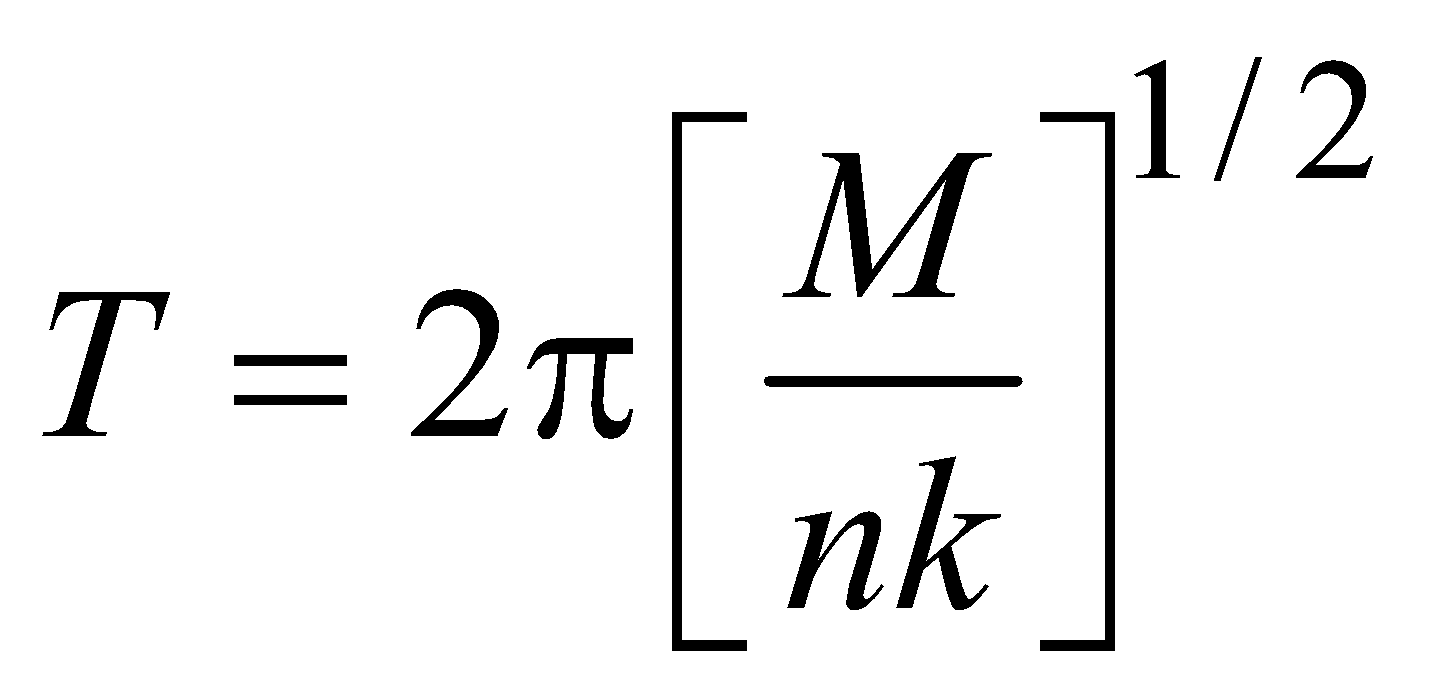
CASE 2 – Simple pendulumA simple pendulum consists of a point mass suspended by a weightless inextensible cord from a rigid support.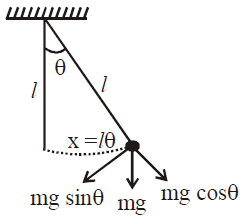
Let a bob of mass m is displaced from its, equilibrium position and released, then it oscillates in a vertical plane under gravity. Let θ be the angular displacement at any time t, then corresponding linear displacement along the arc isx = l θ.It is clear from the diagram that mg sinθ, is the restoring force acting on m tending to return it to mean position. So from Newton’s second law ![]() …(i)where negative sign indicates that restoring force mg sin θ (= F) is opposite to displacement θ. If θ is very small, then
…(i)where negative sign indicates that restoring force mg sin θ (= F) is opposite to displacement θ. If θ is very small, then
sin θ ≈ θ, so from equation (i)![]() …(ii) where ω2 = g/l.This is the equation of S.H.M. of the bob with time period
…(ii) where ω2 = g/l.This is the equation of S.H.M. of the bob with time period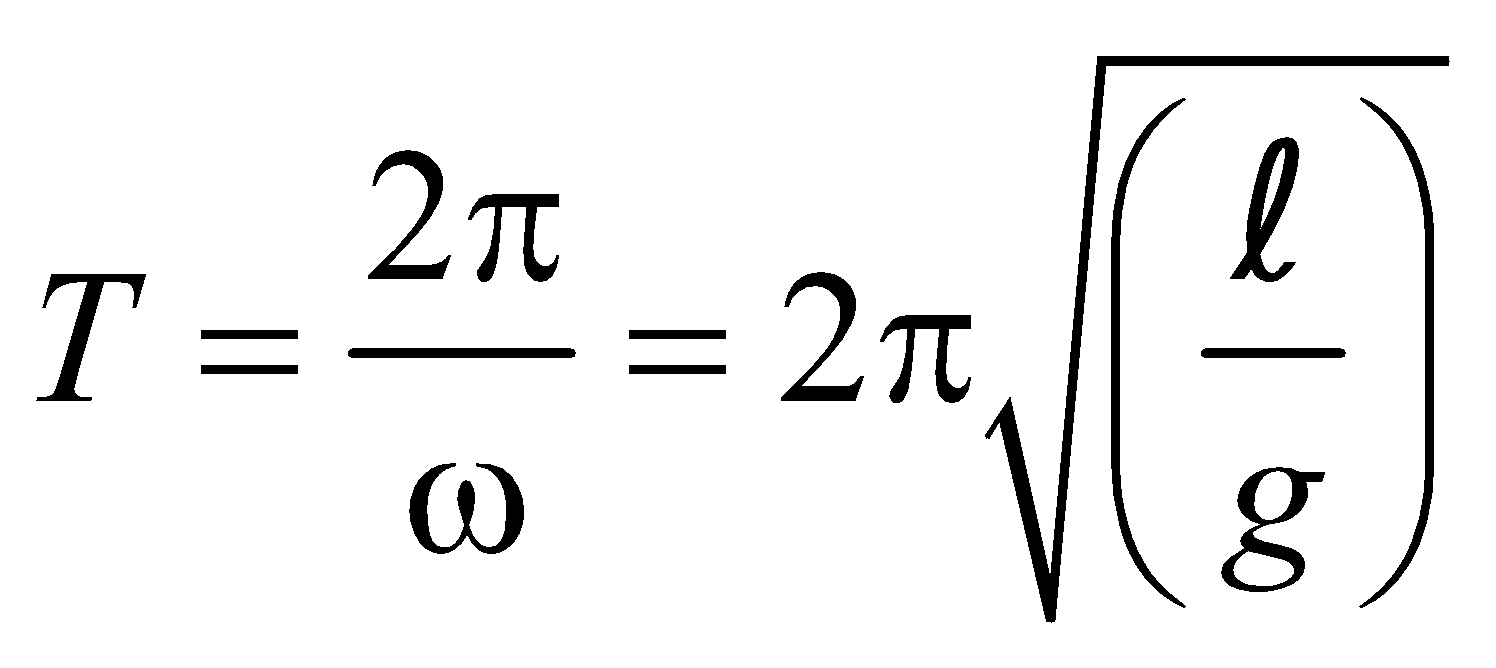
How to find the time period of a body undergoing S.H.M.?Step 1 : First, find the equilibrium position. Equilibrium position will be one for which ![]() and
and ![]() Step 2 : Displace the body from the equilibrium position by x.Find the restoring force acting on the body F = –kx (for translation)Find the restoring torque acting on the body
Step 2 : Displace the body from the equilibrium position by x.Find the restoring force acting on the body F = –kx (for translation)Find the restoring torque acting on the body ![]() (for rotational)Step 3 : Since
(for rotational)Step 3 : Since ![]() ∴ Use
∴ Use ![]() … (i) for translational
… (i) for translational![]() … (ii) for rotationalStep 4 :
… (ii) for rotationalStep 4 : ![]() (for translational)
(for translational)![]() (for rotational) where, I = moment of inertia
(for rotational) where, I = moment of inertia
Common DefaultIncorrect. The time period of spring mass-system is dependent on the value of g. Correct. Time period of spring-mass system shifts only the equilibrium position. It does not change the time period. Because of this reason, time period of spring mass system remains same on plains / mountains / in satellites.Incorrect. The time taken to cover half the amplitude form equilibrium position is ![]() .Correct. The actual time taken is
.Correct. The actual time taken is ![]() .Incorrect. In a spring mass system, mass oscillate about the end of a spring when the spring is in unstretched condition.Correct. The mass oscillates about the equilibrium position which may or may not be at the unstretched length.
.Incorrect. In a spring mass system, mass oscillate about the end of a spring when the spring is in unstretched condition.Correct. The mass oscillates about the equilibrium position which may or may not be at the unstretched length.
CASE 3 – Liquid in U-tubeA U-tube of uniform cross-sectional area A has been set up vertically with open ends facing up.
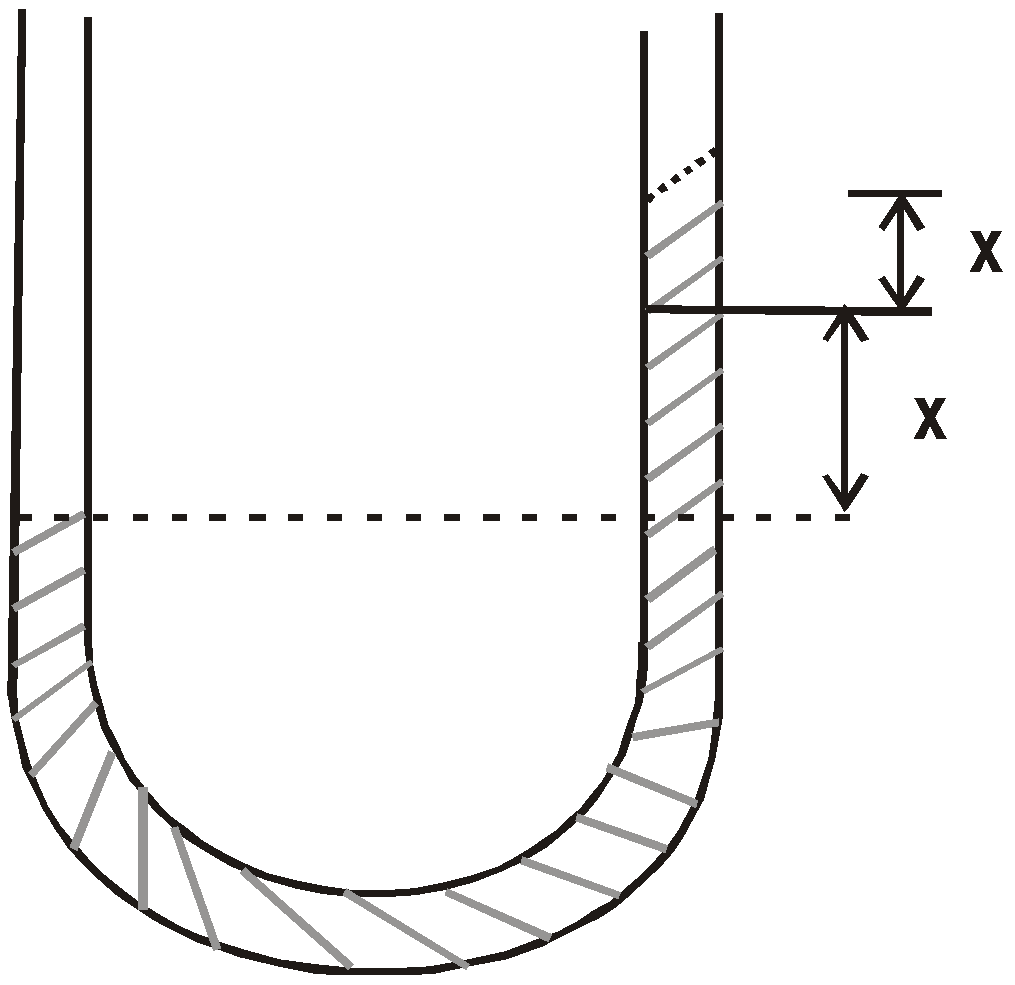
[Restoring force = –2Adg x] If m gm of a liquid of density d is poured into it then time period of oscillation.
CASE 4 – Rectangular block in liquid Rectangular block floating in a liquid,
Rectangular block floating in a liquid, ![]()
where d = density of liquid, d′ = density of block, h = height of block
CASE 5 – Vibration of gas system in a cylinder with frictionless piston.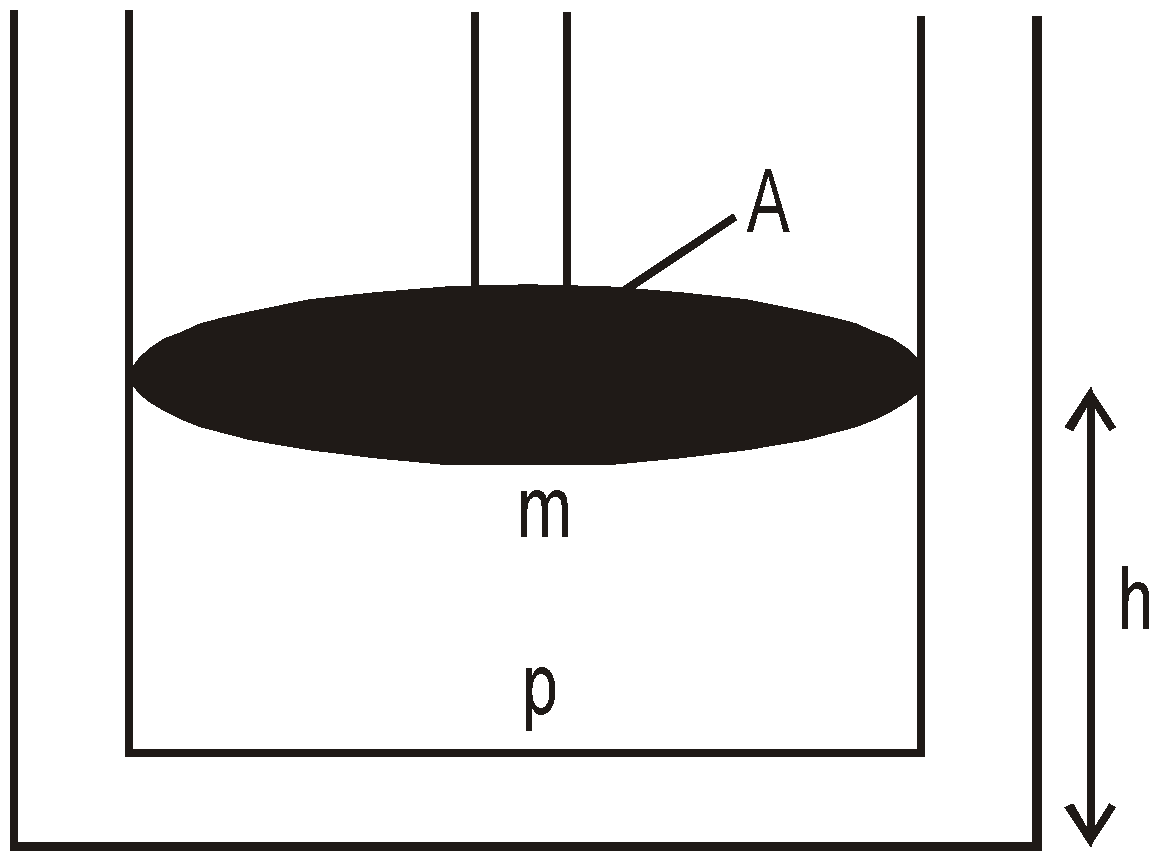 Time period,
Time period, ![]() where m = mass of gas, A = cross sectional area of pistonP = pressure exerted by gas on the piston, h = height of piston
where m = mass of gas, A = cross sectional area of pistonP = pressure exerted by gas on the piston, h = height of piston
CASE 6 – If a tunnel is dig in the earth diametrically or along a chord then time period, ![]() for a particle released in the tunnel.CASE 7 – The time period of a ball oscillating in the neck of a chamber
for a particle released in the tunnel.CASE 7 – The time period of a ball oscillating in the neck of a chamber ![]()
CASE 8 – If a dipole of dipole moment p is suspended in a uniform electric field E then time period of oscillation ![]() KEEP IN MEMORY
KEEP IN MEMORY
- In S.H.M. the phase relationship between displacement, velocity and acceleration, is as follows :
- The velocity is leading the displacement by a phase
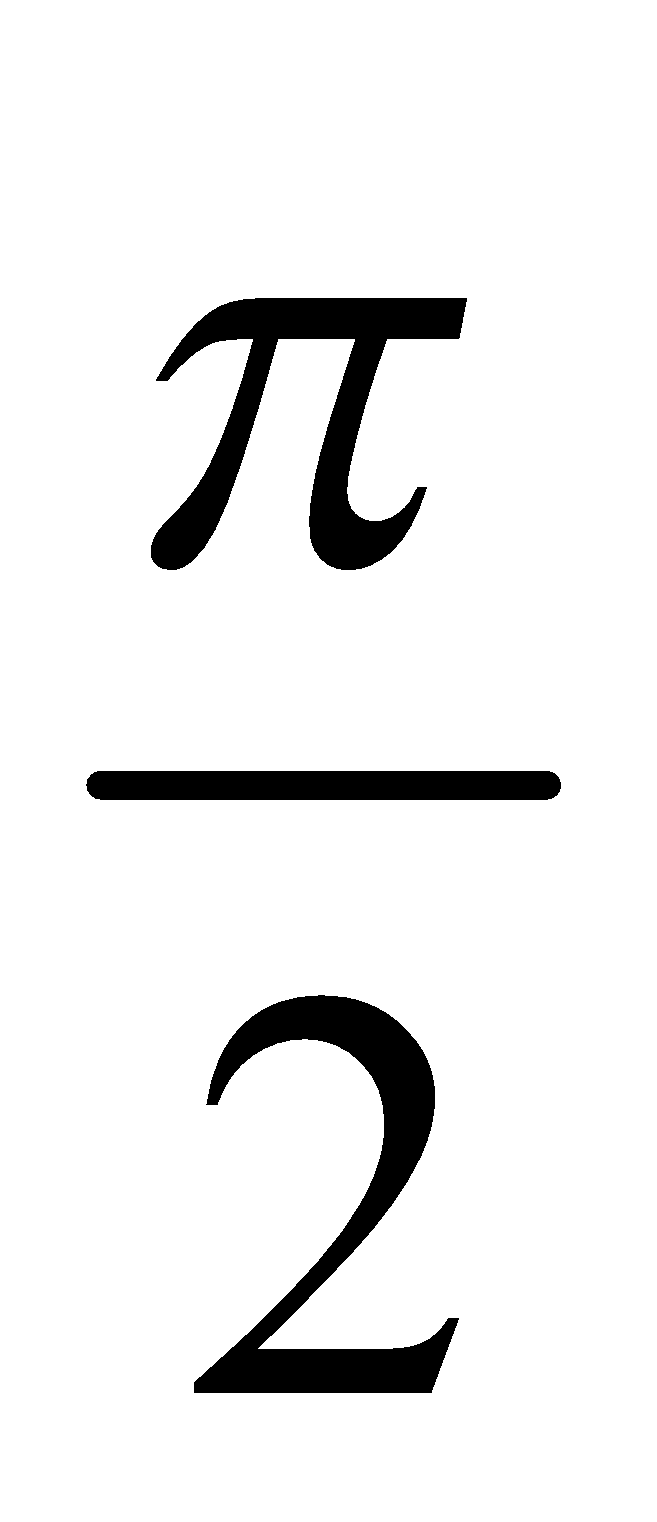 radian
radian - The acceleration is leading the displacement by a phase π radian
- The acceleration is leading the velocity by a phase
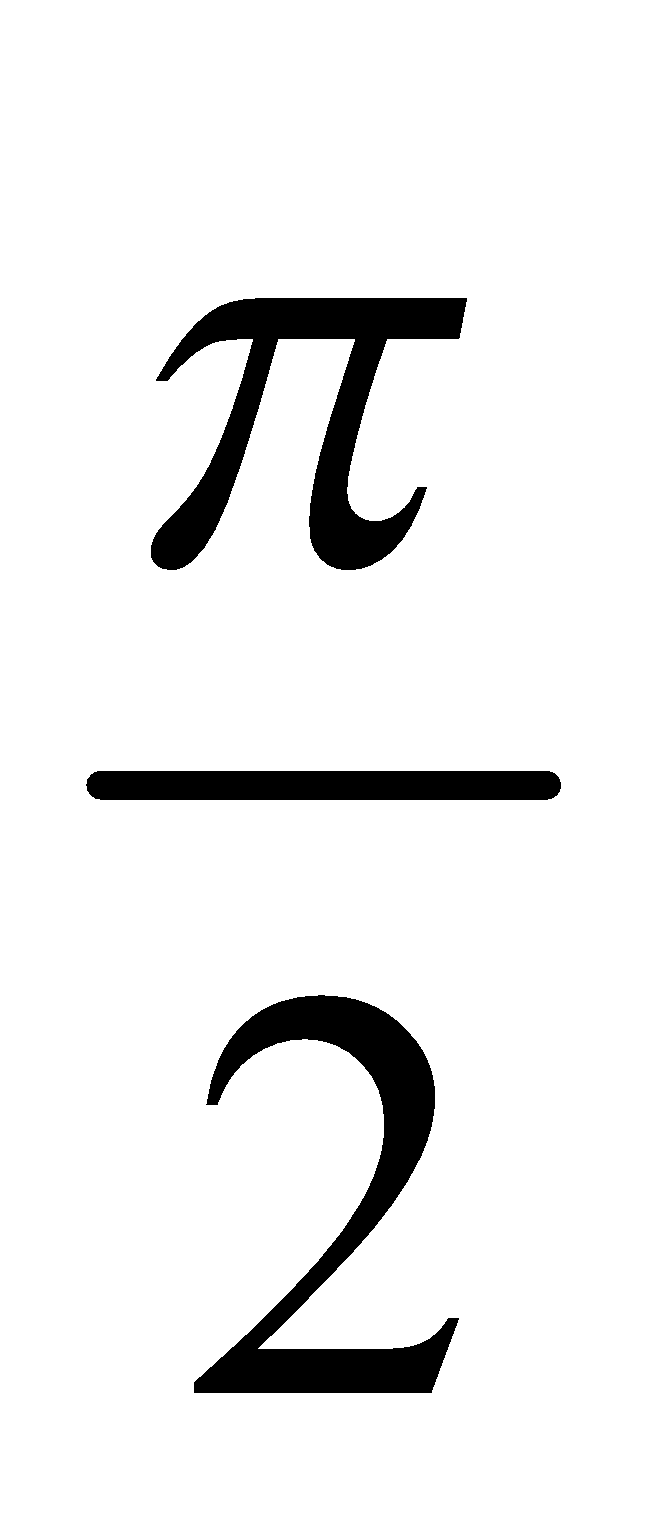 radian.
radian. - When
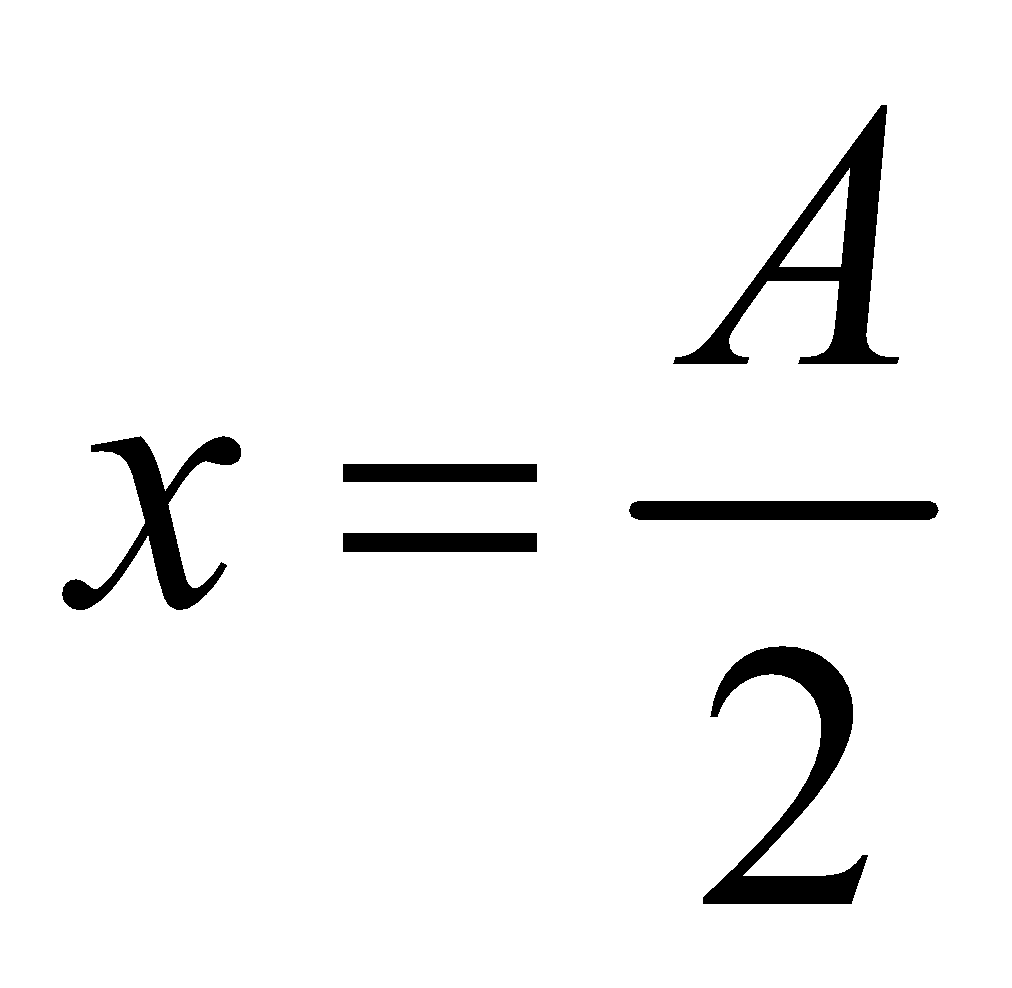 , then velocity V = 0.86Vmax.
, then velocity V = 0.86Vmax. - When V = Vmax/2, the displacement x = 0.87A.
- When
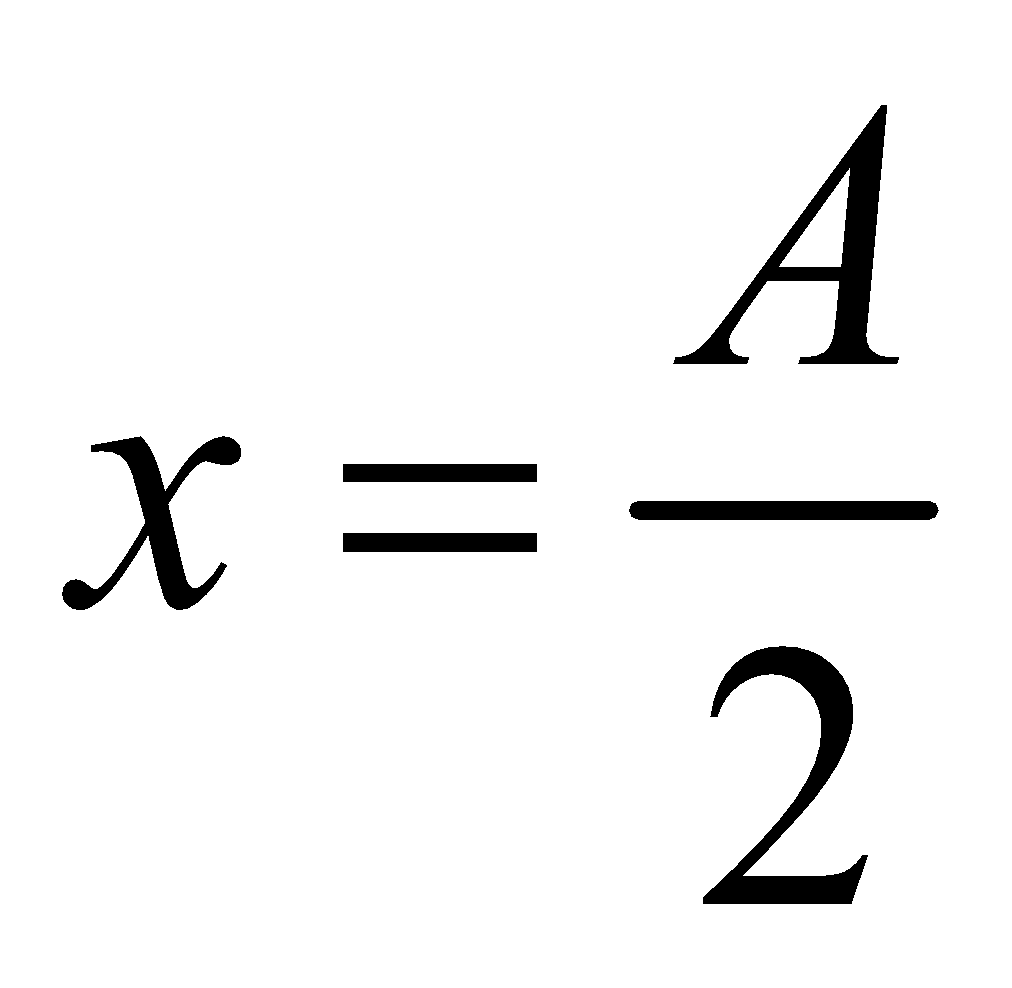 , the kinetic energy of S.H.M. is 75% of the total energy and potential energy 25% of the total energy.
, the kinetic energy of S.H.M. is 75% of the total energy and potential energy 25% of the total energy. - When the kinetic energy of S.H.M. is 50% of the total energy, the displacement is 71% of the amplitude.
- The velocity is leading the displacement by a phase
- The time period of a simple pendulum of length l which is comparable with radius of earth.
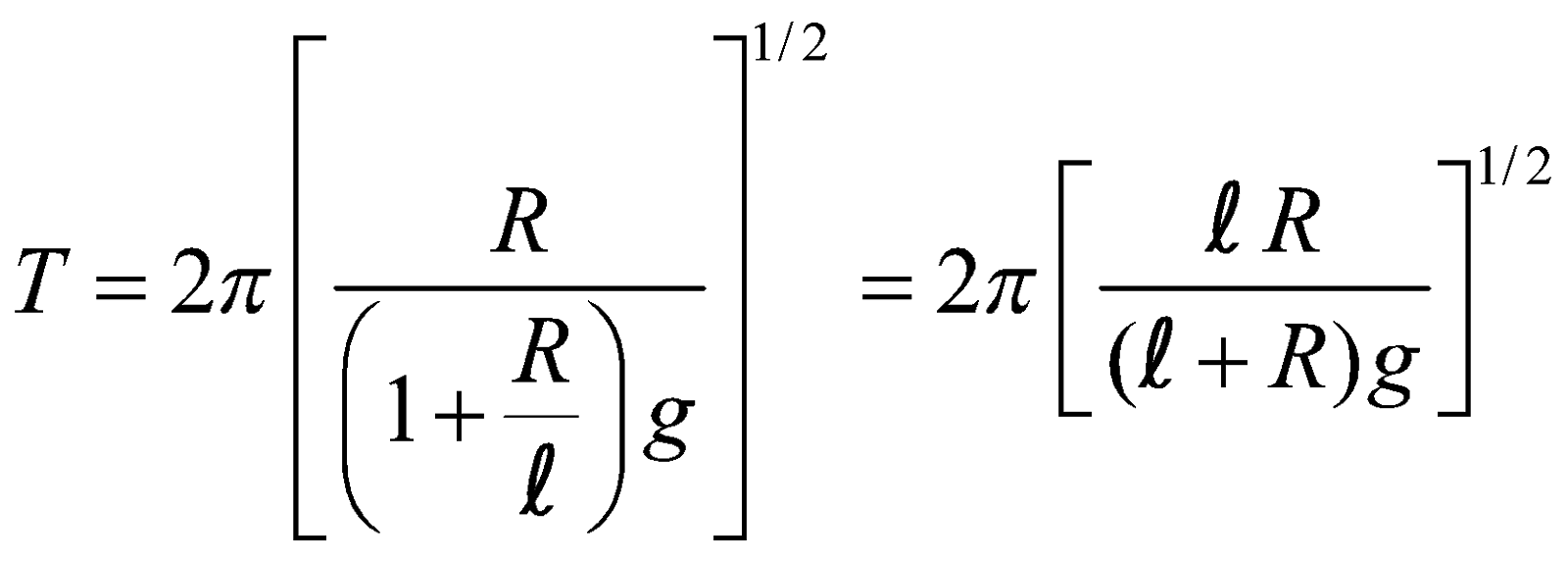 where R = radius of the earth and g is the acceleration due to gravity on the surface of the earth.
where R = radius of the earth and g is the acceleration due to gravity on the surface of the earth.
- When l << R, then

- When l = R, we find
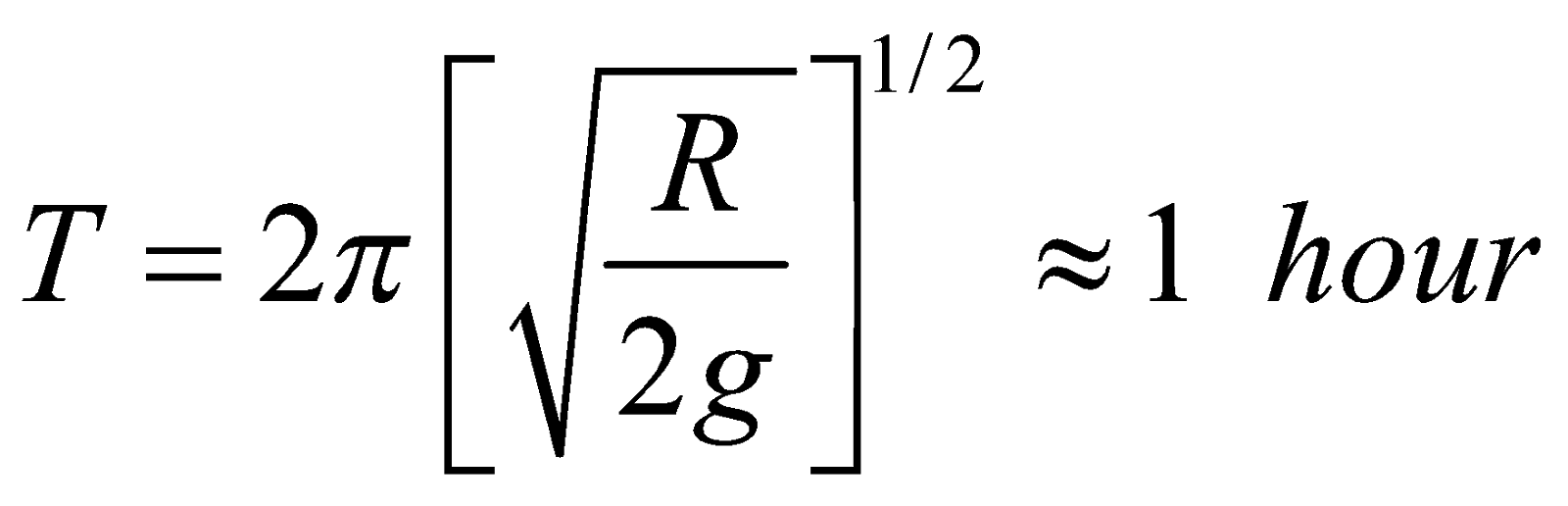
- When l =
 , then
, then
- When l << R, then
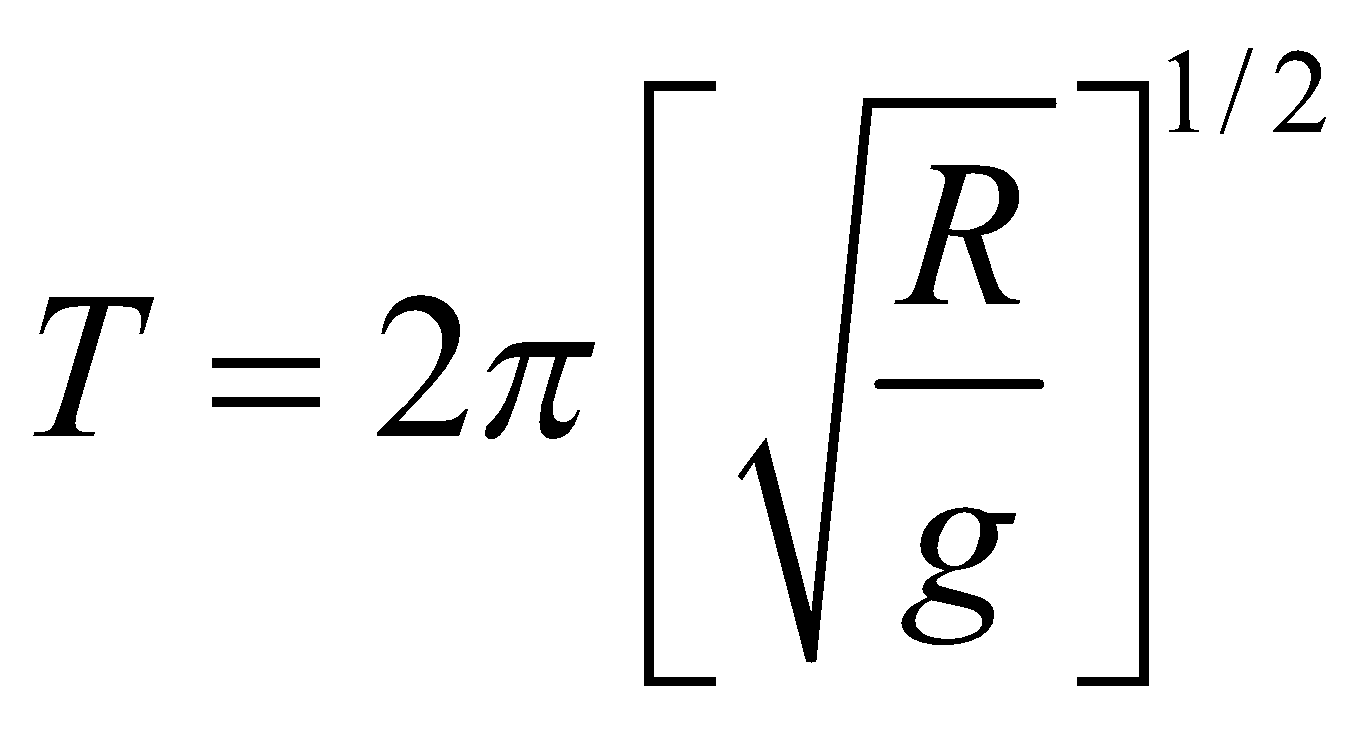 = 84.6 minutes. Thus maximum of T is 84.6 minutes.
= 84.6 minutes. Thus maximum of T is 84.6 minutes.
- Under weightlessness or in the freely falling lift
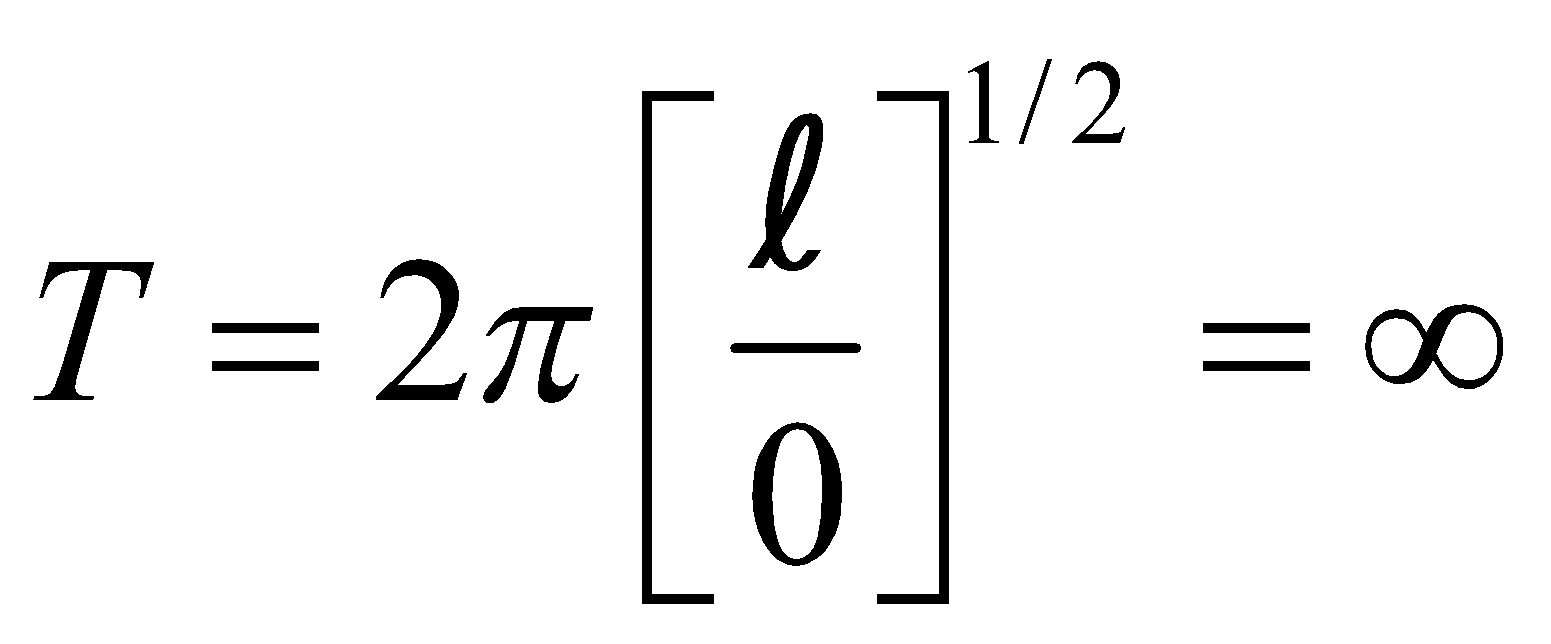
This means, the pendulum does not oscillate at all.
- Under weightlessness or in the freely falling lift
- Time period of a simple pendulum in a train accelerating or retarding at the rate a is given by
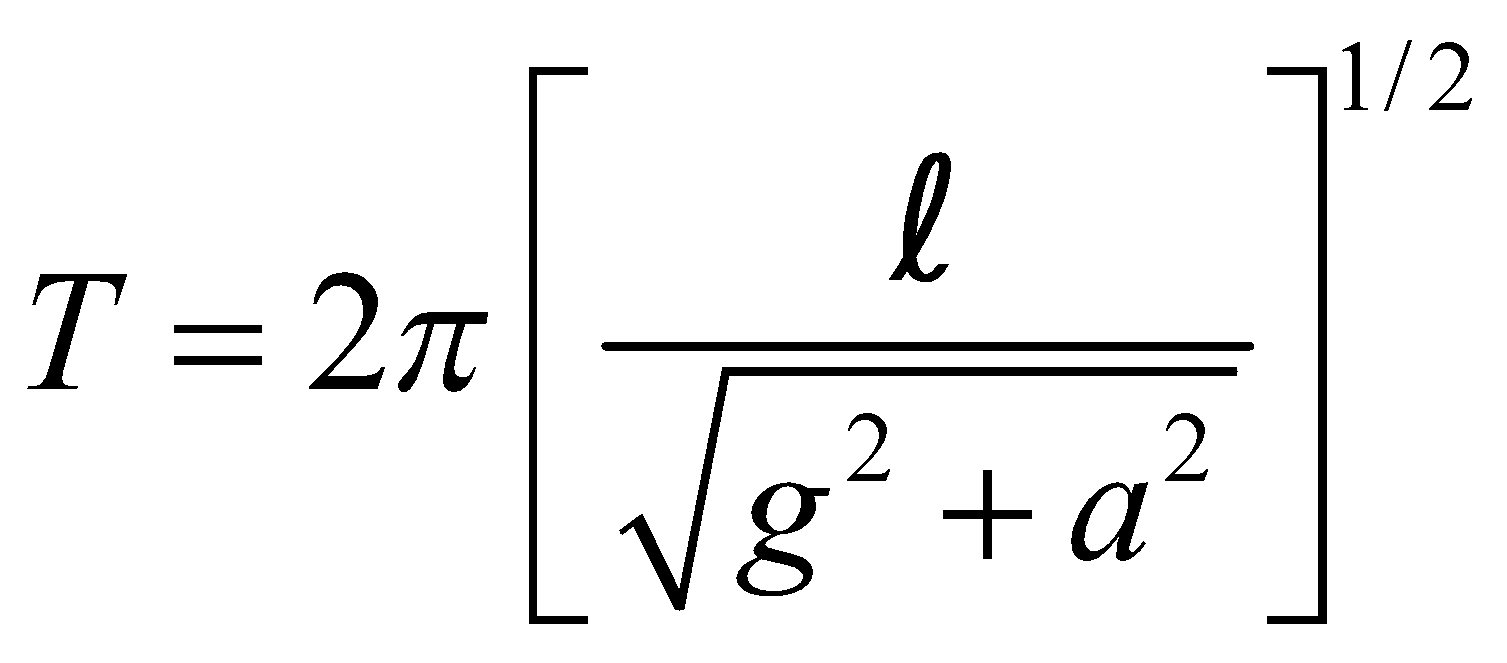
- If a simple pendulum whose bob is of density do is made to oscillate in a liquid of density d, then its time period of vibration in liquid will increase and is given by
 (where d0 > d)
(where d0 > d)
- The time period of a simple pendulum in a vehicle moving along a circular path of radius r and with constant velocity V is given by,
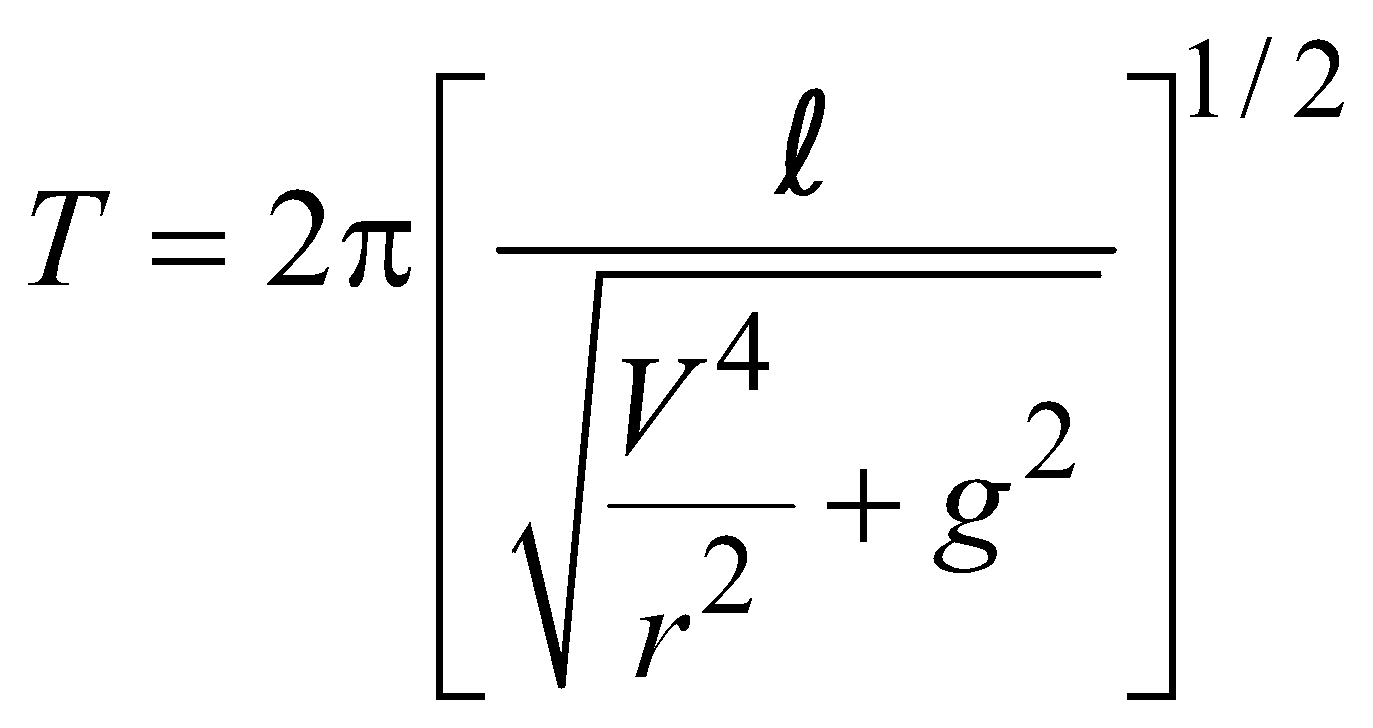
- If T1 and T2 are the time periods of a body oscillating under the restoring force F1 and F2 then the time period of the body under the influence of the resultant force
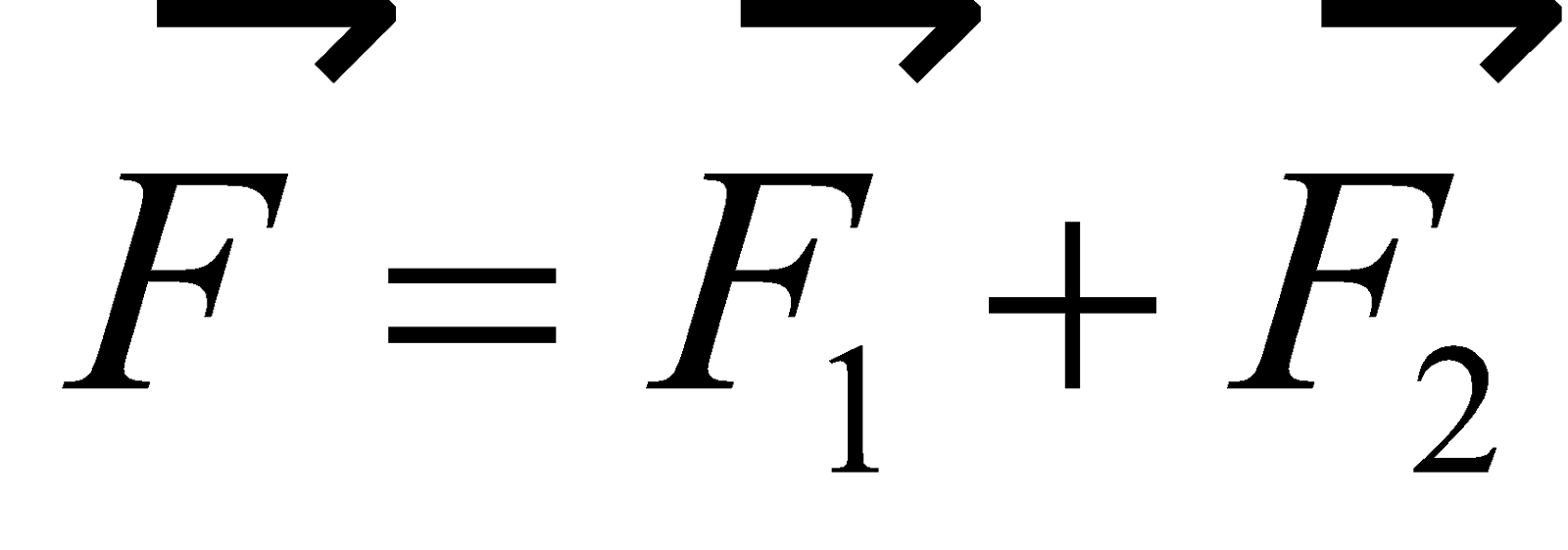 will be
will be 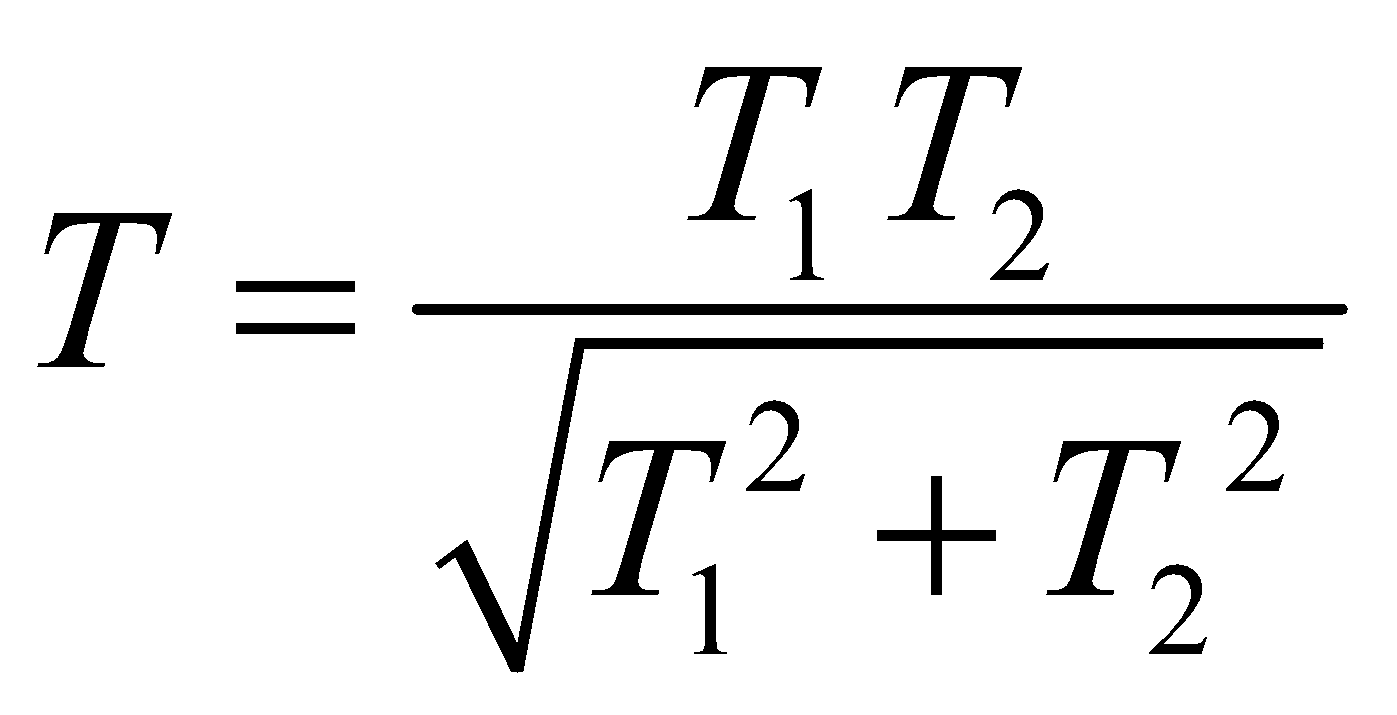
- (a) The percentage change in time period of simple pendulum when its length changes is
(b) The percentage change in time period of simple pendulum when g changes but l remains constant is ![]() (c) The percentage change in time period of simple pendulum when both l and g change is
(c) The percentage change in time period of simple pendulum when both l and g change is ![]()
- If a wire of length l, area of cross-section A, Young’s modulus Y is stretched by suspending a mass m, then the mass can oscillate with time period
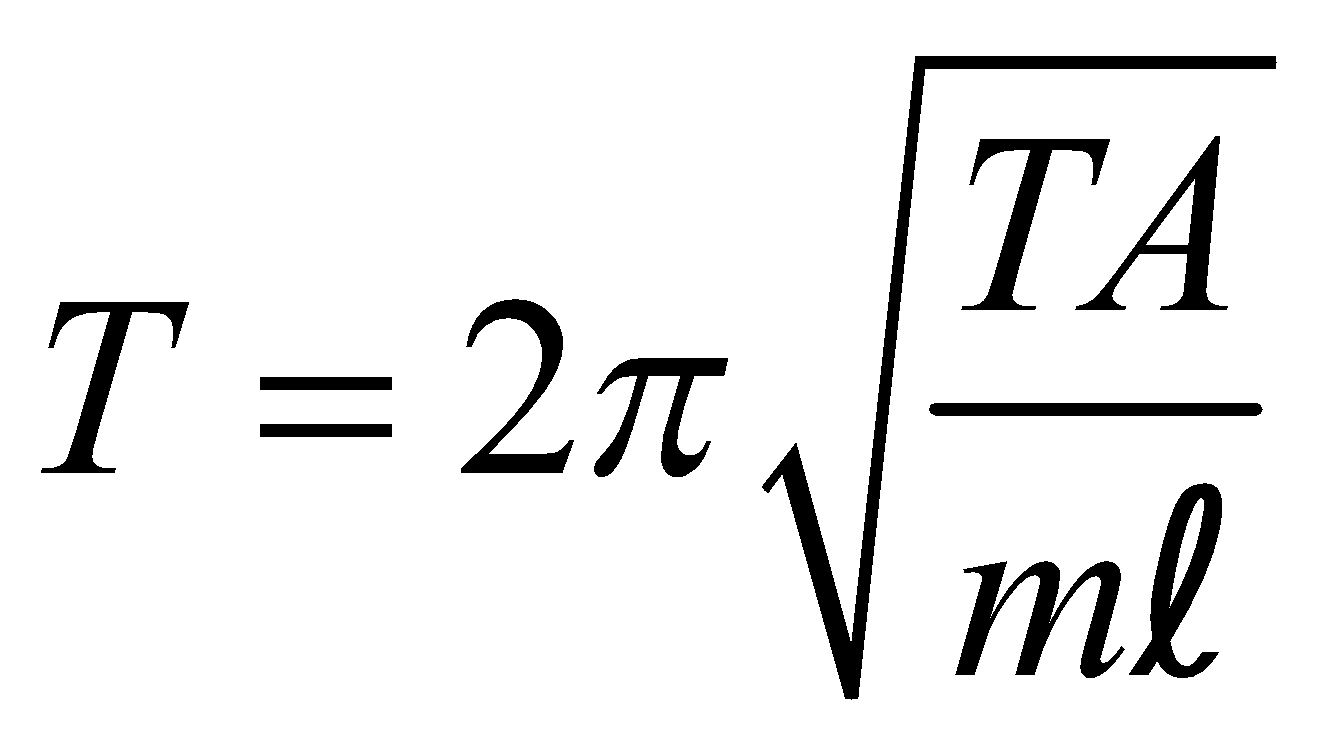
- If a simple pendulum is suspended from the roof of compartment of a train moving down an inclined plane of inclination θ, then the time period of oscillations
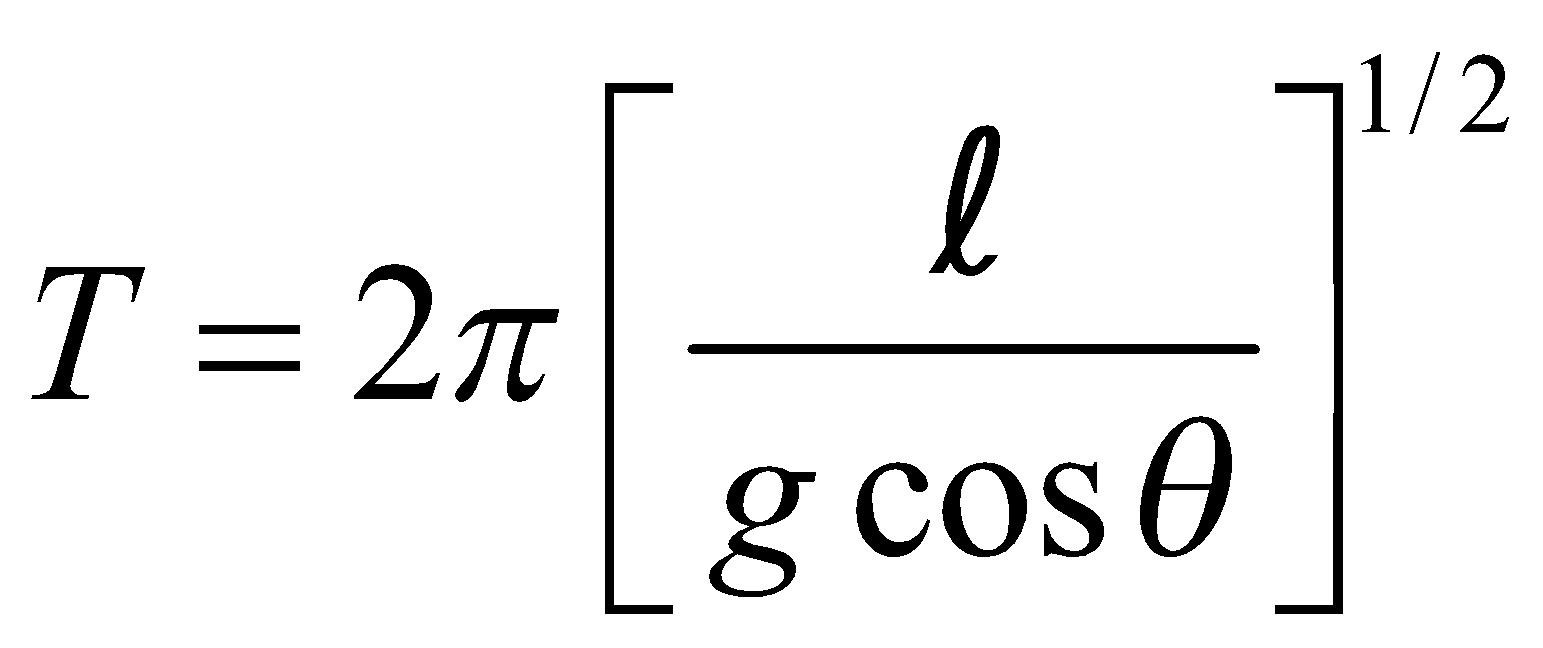
- If a ball of radius r oscillates in a bowl of radius R, then its time period is given by :
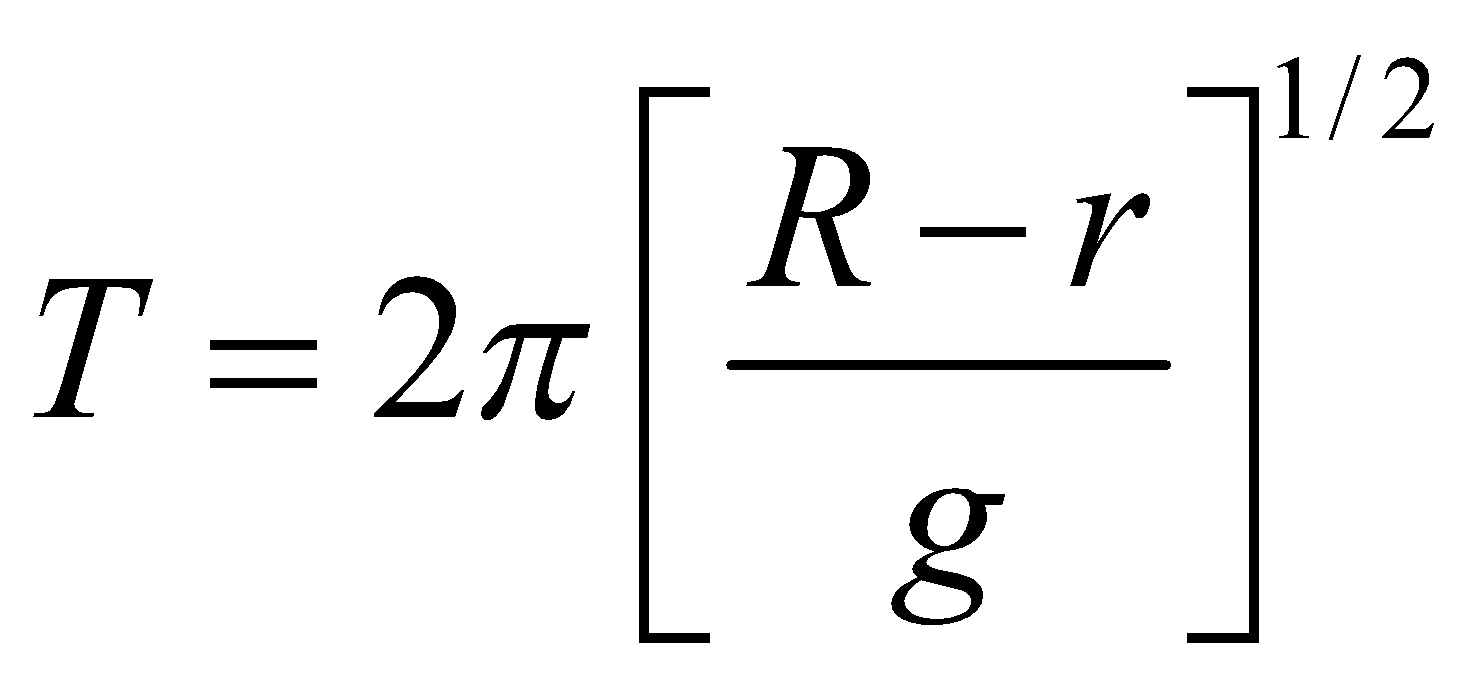
- If a disc of radius r oscillates about a point at its rim, then its time period is given by:
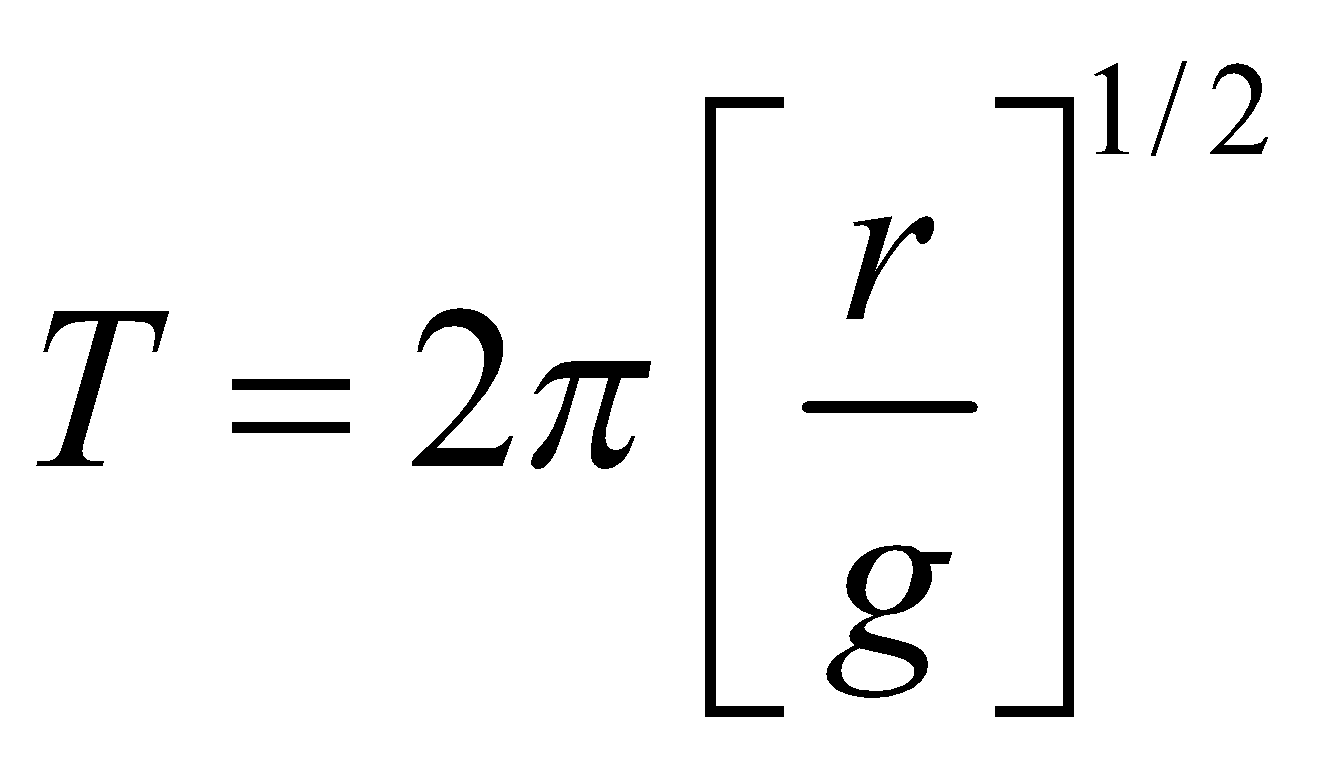
It behaves as a simple pendulum of length r.
- The graph between the length of a simple pendulum and its time period is a parabola.
- The graph between the length of a simple pendulum and the square of its time period is a straight line.
- The graph between l & T and between l & T2 intersect at T = 1 second.
- The time period of the mass attached to spring does not change with the change in acceleration due to gravity.
- If the mass m attached to a spring oscillates in a non-viscous liquid density σ, then its time period is given by
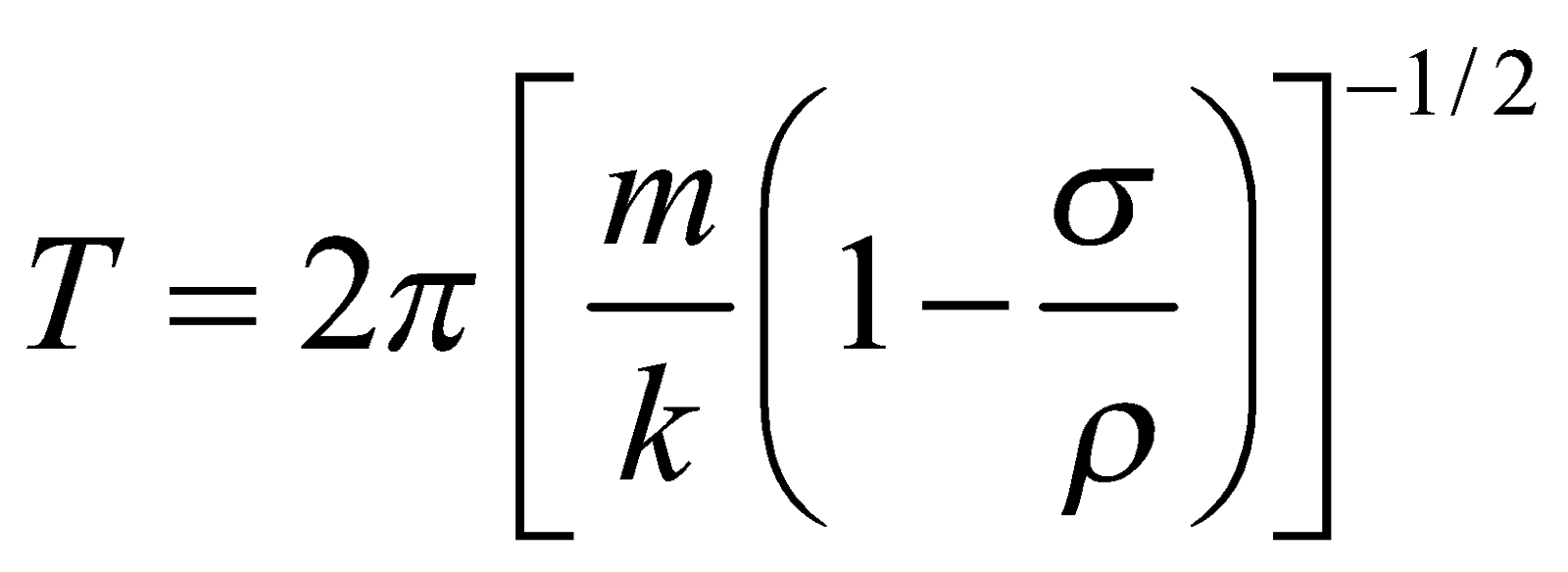
where k = force constant and is density of the mass suspended from the spring.
- The length of second pendulum (T = 2 sec) is 99 cm
PHYSICAL PENDULUM
Trestoring = – mgd sin θ If θ is small, sin θ ≈ θ∴ Trestoring = – mgdθ 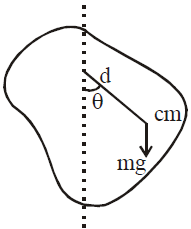 and
and ![]() Let a test-tube of radius r, carrying lead shots of mass m is held vertically when partly immersed in liquid of density ρ. On pushing the tube little into liquid and let it executes S.H.M. of time period
Let a test-tube of radius r, carrying lead shots of mass m is held vertically when partly immersed in liquid of density ρ. On pushing the tube little into liquid and let it executes S.H.M. of time period 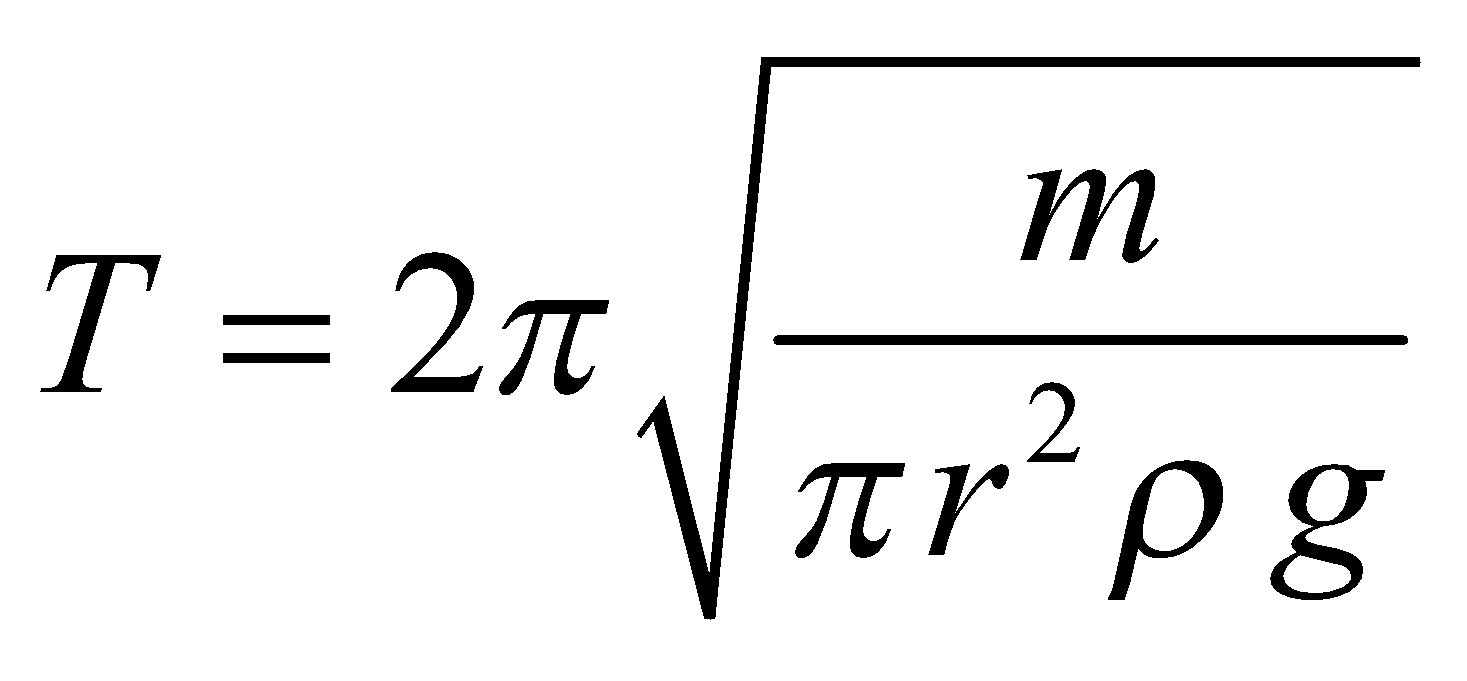
CONICAL PENDULUM
When the bob of a simple pendulum moves in a horizontal circle it is called as conical pendulum. 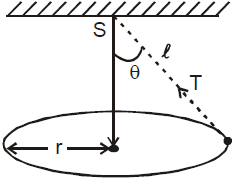
If l is the length of the pendulum and the string makes an angle θ with vertical then time period, ![]()
TORSIONAL PENDULUM
It is an arrangement which consists of a heavy mass suspended from a long thin wire whose other and is clamped to a rigid support. Time period![]() where I = moment of inertia of body about the suspension wire as axis of rotation.C = restoring couple per unit thirst.
where I = moment of inertia of body about the suspension wire as axis of rotation.C = restoring couple per unit thirst.
KEEP IN MEMORY
- The displacement, velocity and acceleration of S.H.M. vary simple harmonically with the same time period and frequency.
- The kinetic energy and potential energy vary periodically but not simple harmonically. The time period of kinetic energy or potential energy is half that of displacement, velocity and acceleration.
- The graph between displacement, velocity or acceleration and t is a sine curve. But the graph between P.E. or K.E. of S.H.M. and time t is parabola.
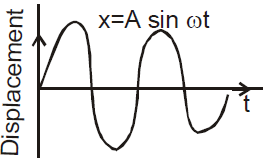

- If the bob of simple pendulum is -vely charged and a +vely charged plate is placed below it, then the effective acceleration on bob increases and consequently time period decreases.
Time period, 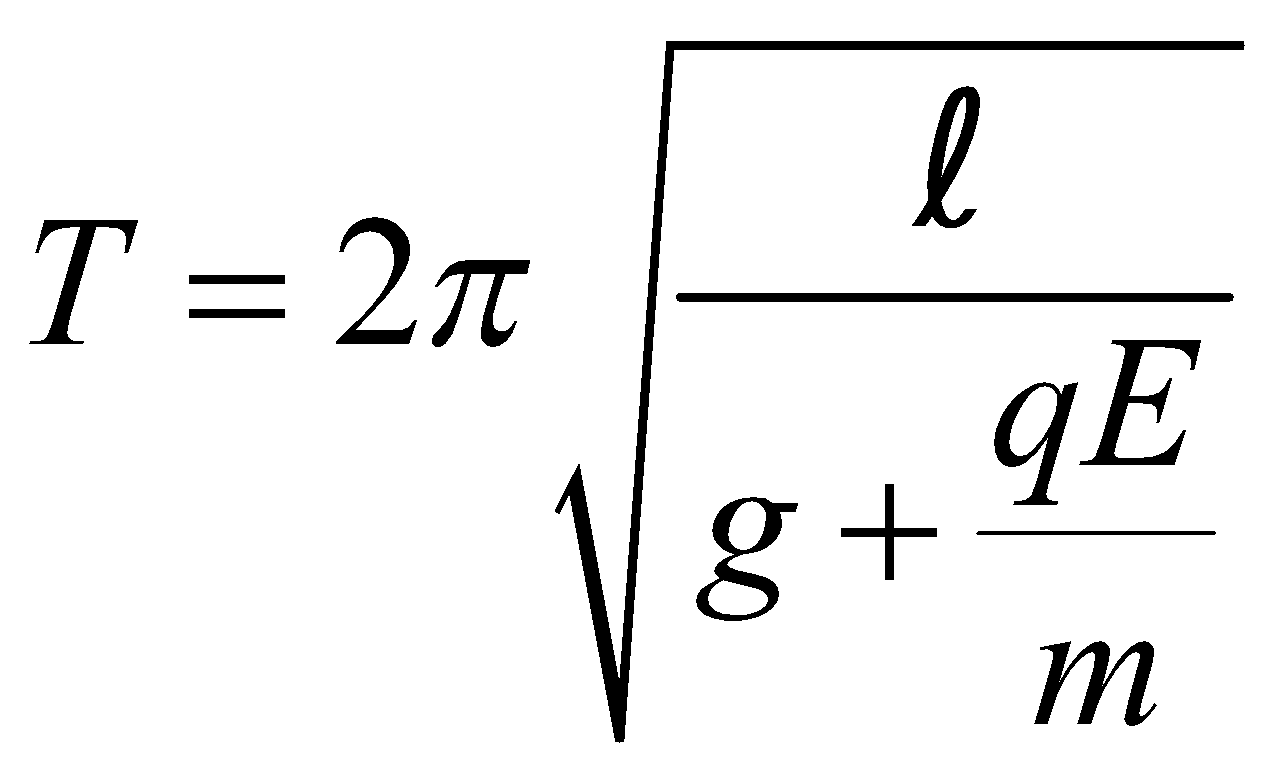 In this case electric force q E and gravity force act in same direction.
In this case electric force q E and gravity force act in same direction.
- If the bob of a simple pendulum is -vely charged and is made to oscillate above the -vely charged plate, then the effective acceleration on bob decreases and the time period increases.
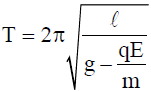
In this case electric force qE and gravity force are opposite.
- A pendulum clock slows down in summer and goes faster in winter.
- Potential energy of a particle executing S.H.M. is equal to average force × displacement.
i.e., . 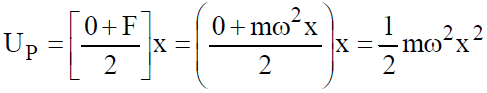
- If the total energy of a particle executing S.H.M. is E, then its potential energy at displacement x is
![]() and kinetic energy
and kinetic energy 
FREE, DAMPED, FORCED OSCILLATIONS AND RESONANCE
FREE OSCILLATION
If a system oscillates on its own and without any external influence then it is called as free oscillation. Frequency of free oscillation is called natural frequency. The equation for free S.H.M. oscillation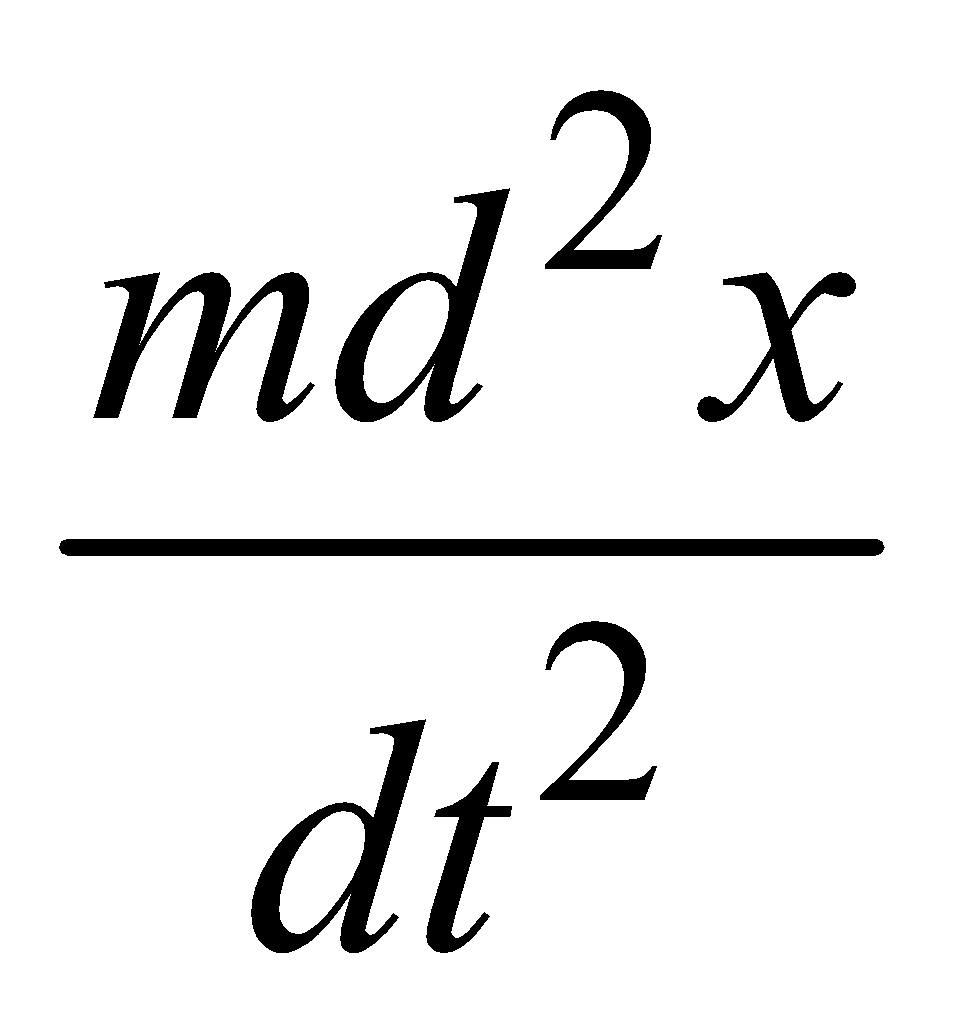 = Frestoring force = –kx, where k is constant.The differential equation of harmonic motion in absence of damping and external force is
= Frestoring force = –kx, where k is constant.The differential equation of harmonic motion in absence of damping and external force is 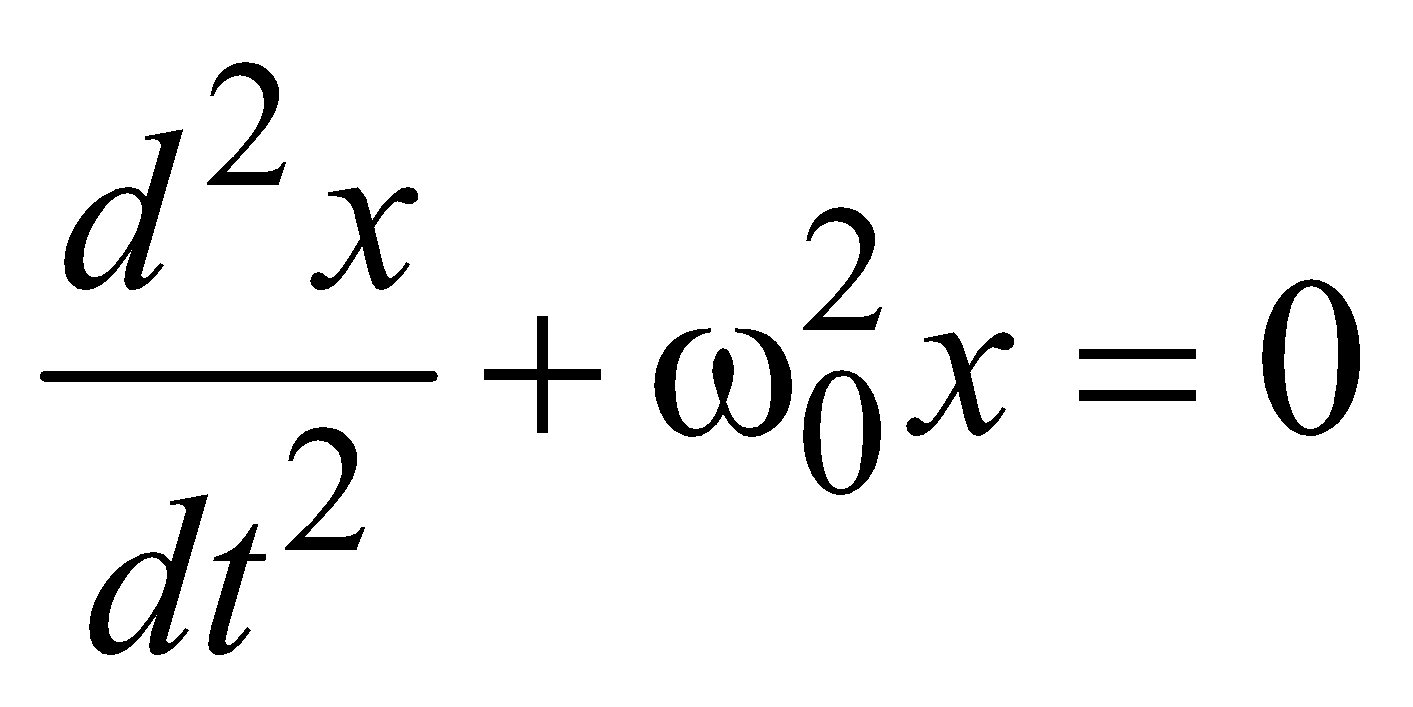 , where ω0 is natural frequency of body. The time period is
, where ω0 is natural frequency of body. The time period is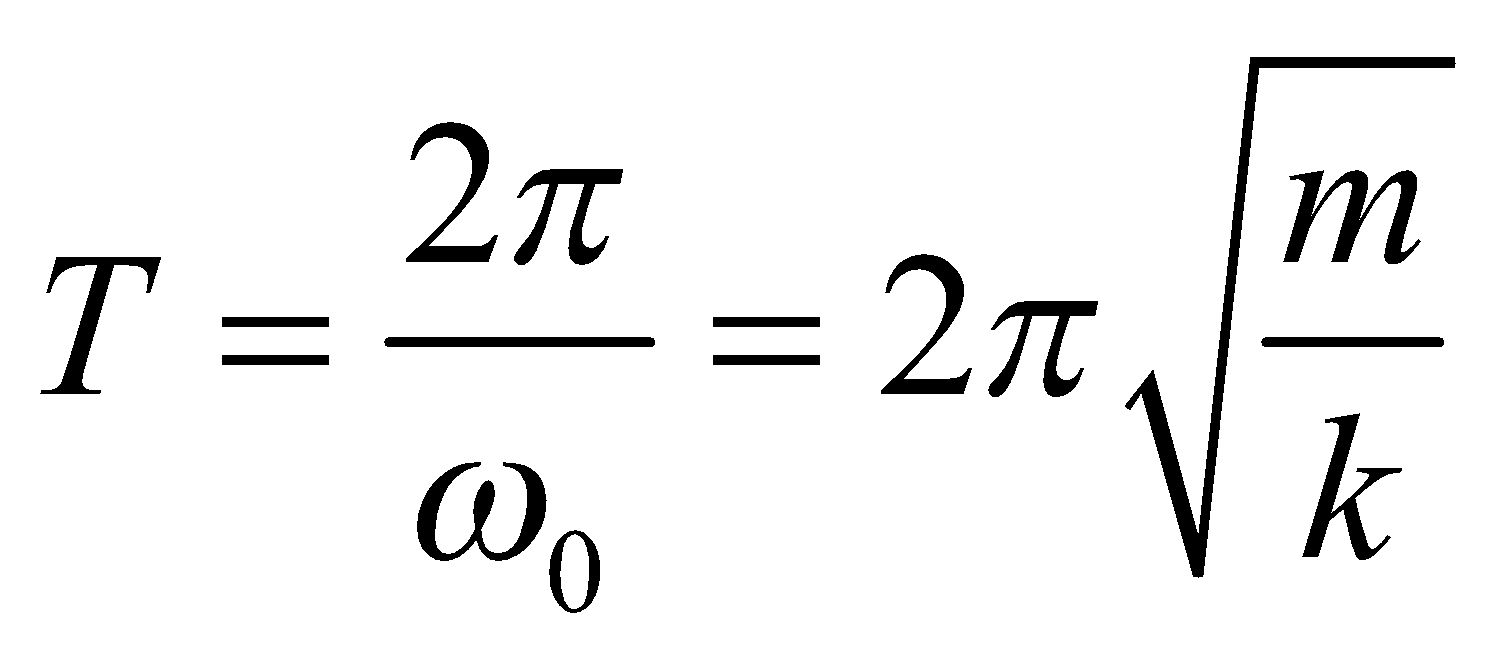
DAMPED OSCILLATION
Oscillation performed under the influence of frictional force is called as damped oscillation.In case of damped oscillations the amplitude goes on decreasing and ultimately the system comes to a rest.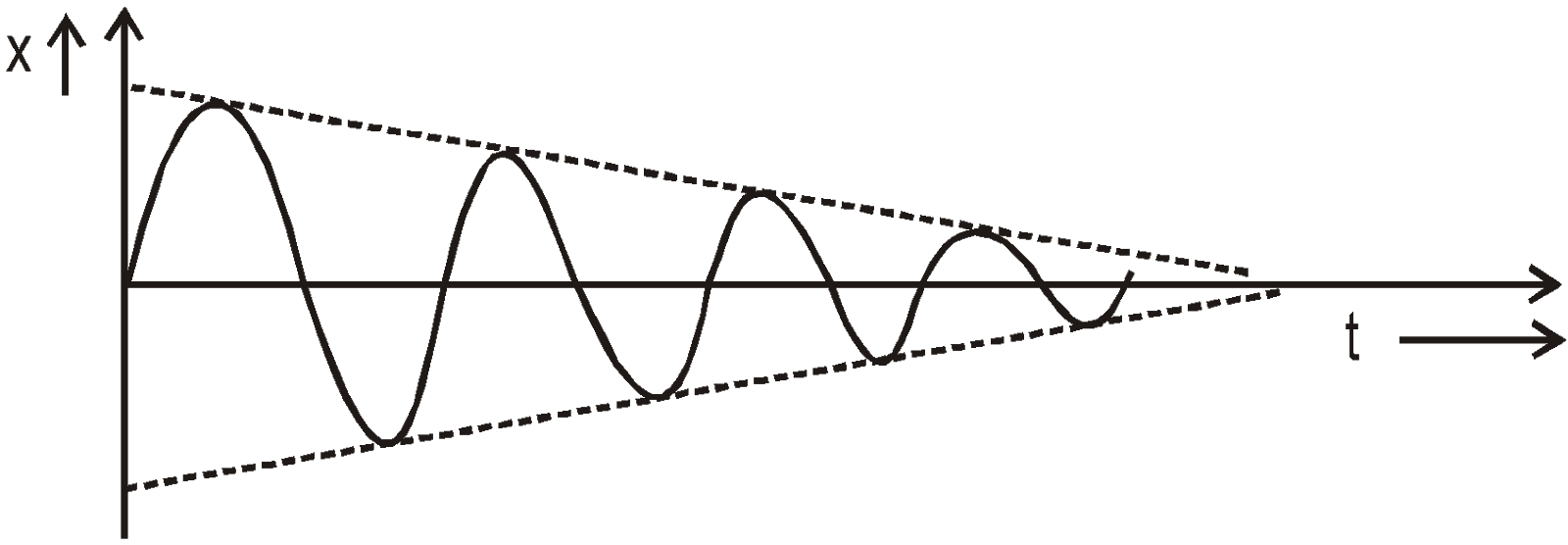 The damping force (Fdamping ∝ – v ⇒ Fdamping = – bv) is proportional to the speed of particle. Hence the equation of motion
The damping force (Fdamping ∝ – v ⇒ Fdamping = – bv) is proportional to the speed of particle. Hence the equation of motion ![]() where b is positive constant and is called damping coefficient. Then the differential equation of a damped harmonic oscillation is
where b is positive constant and is called damping coefficient. Then the differential equation of a damped harmonic oscillation is 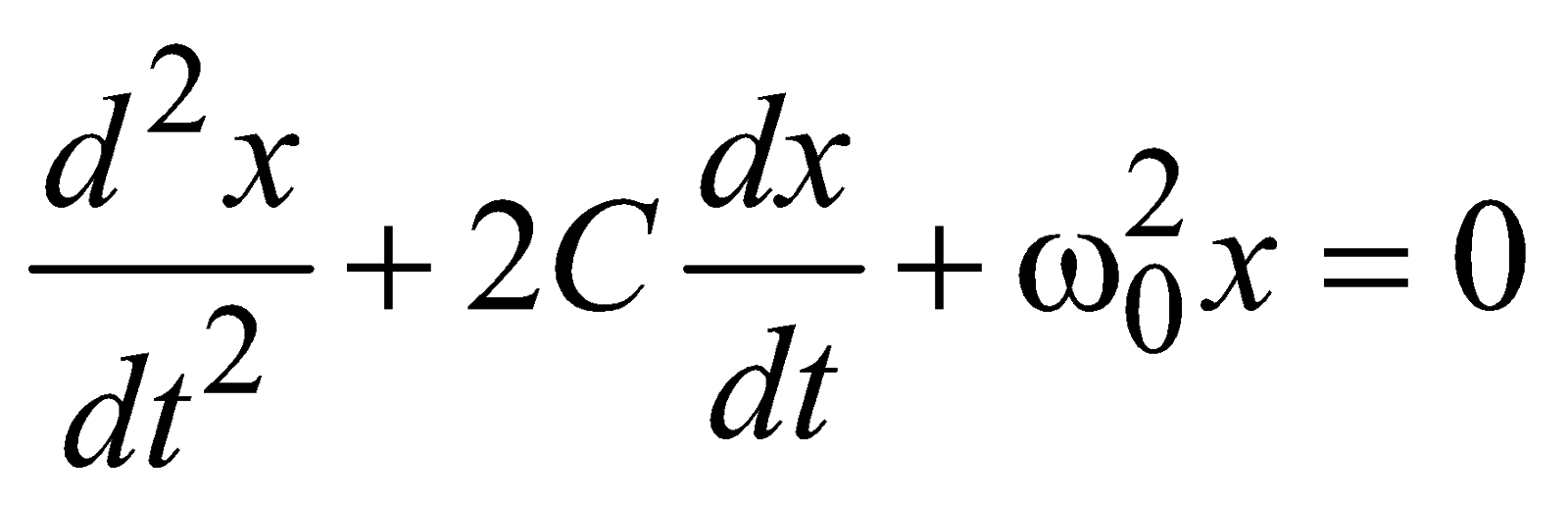 …(i)where 2 C = b/m (C is damping constant) &
…(i)where 2 C = b/m (C is damping constant) & ![]() , the natural frequency of oscillating particle i.e., its frequency in absence of damping.
, the natural frequency of oscillating particle i.e., its frequency in absence of damping.
In case of overdamping the displacement of the particle is ![]() sin (ωt + φ) …(ii)⇒ x = A sin (ωt + φ) where A0 = max. amplitude of the oscillator.
sin (ωt + φ) …(ii)⇒ x = A sin (ωt + φ) where A0 = max. amplitude of the oscillator. ![]() and
and ![]() (relaxation time)It is clear from the fig & eqn. (ii) that the amplitude of damped harmonic oscillator decreases with time. In this case, the motion does not repeat itself & is not periodic in usual sense of term. However it has still a time period,
(relaxation time)It is clear from the fig & eqn. (ii) that the amplitude of damped harmonic oscillator decreases with time. In this case, the motion does not repeat itself & is not periodic in usual sense of term. However it has still a time period, ![]() , which is the time interval between its successive passage in same direction passing the equilibrium point.
, which is the time interval between its successive passage in same direction passing the equilibrium point.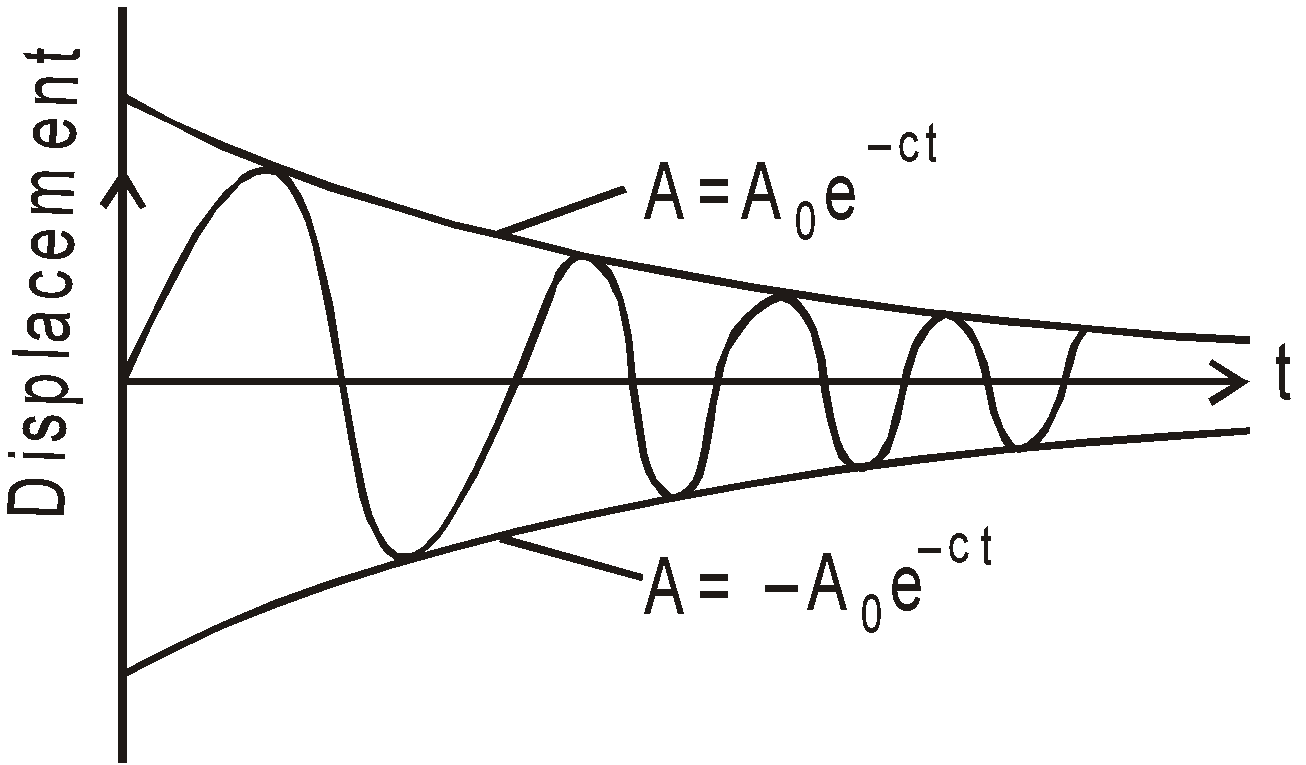
FORCED OSCILLATION AND RESONANCE
The oscillation of a system under the action of external periodic force is called forced oscillation. External force can maintain the amplitude of damped oscillation. When the frequency of the external periodic force is equal to the natural frequency of the system, resonance takes place.
The amplitude of resonant oscillations is very very large. In the absence of damping, it may tend to infinity. At resonance, the oscillating system continuously absorbs energy from the agent applying external periodic force. In case of forced oscillations, the total force acting on the system is 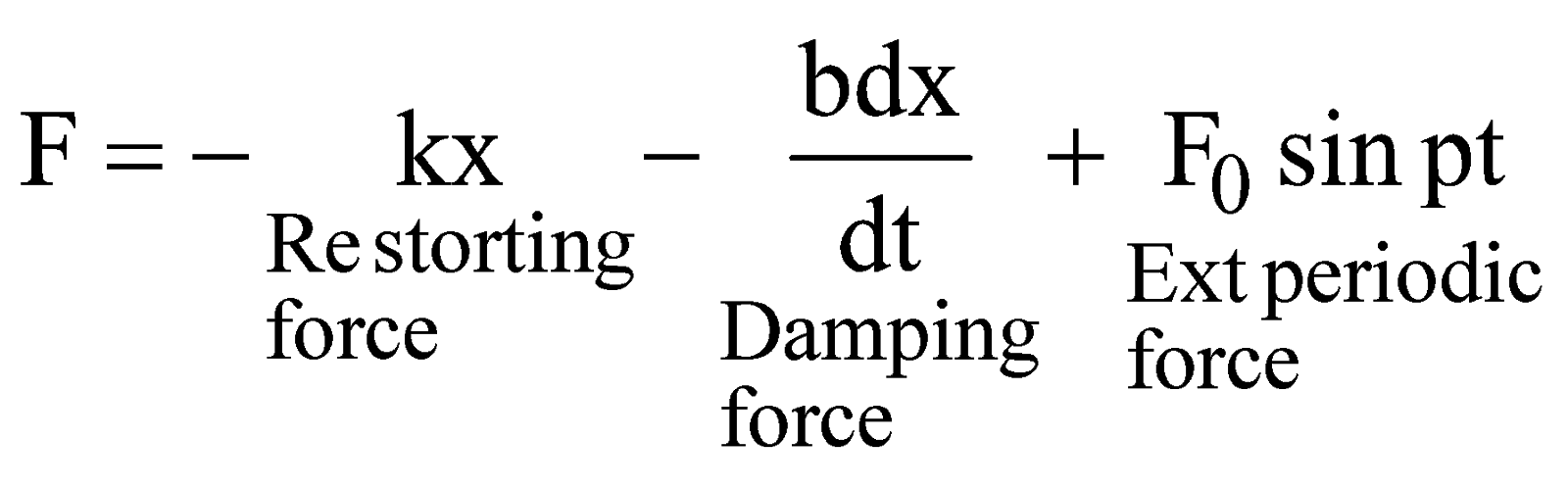 …… (i)Then by Newton’s second law : ⇒
…… (i)Then by Newton’s second law : ⇒ ![]() or
or ![]() …… (ii)where
…… (ii)where ![]() The equation (ii) is the differential equation of motion of forced harmonic oscillator. The amplitude at any time t is
The equation (ii) is the differential equation of motion of forced harmonic oscillator. The amplitude at any time t is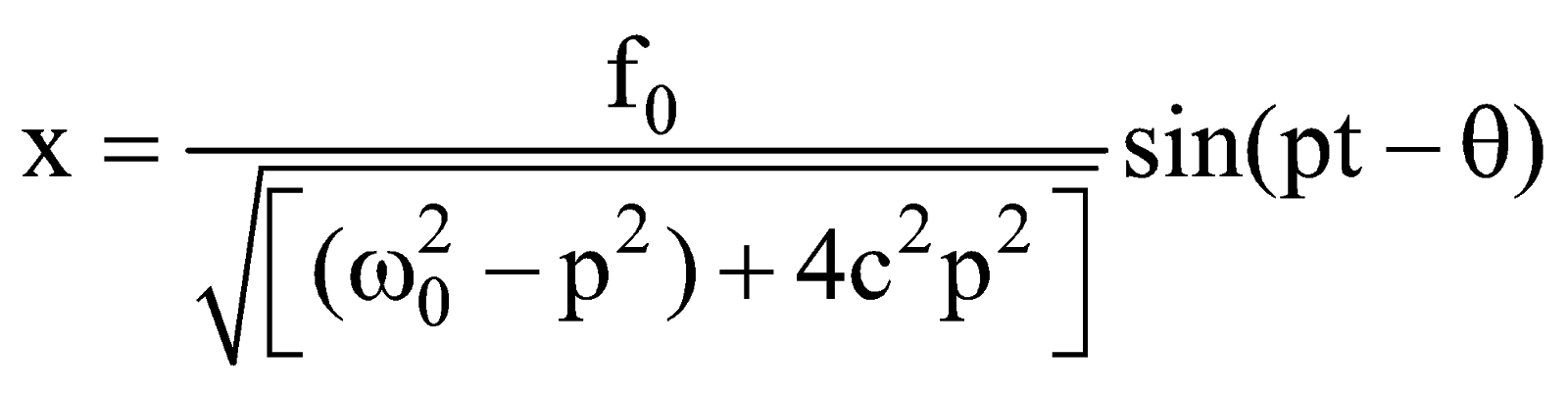 where
where ![]() & p is the frequency of external periodic force.
& p is the frequency of external periodic force.
