Question 5. [Maximum mark: 6]
A garden has a triangular sunshade suspended from three points A(2, 0, 2), B(8, 0, 2) and C(5, 4, 3),
relative to an origin in the corner of the garden. All distances are measured in metres
a (i) Find ⟶CA .
(ii) Find ⟶CB . [2]
(b)Find ⟶CA × ⟶CB . [2]
(c)Hence find the area of the triangle ABC. [2]
▶️Answer/Explanation
(a) (i)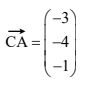 
(ii) 
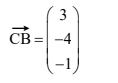(b)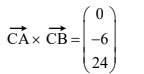 
Note: Do not award (M1) if less than 2 entries are correct. (c) area is \(\frac{1}{2}\sqrt{6^{2}+24^{2} }\) = 12.4 m2
Question
A vertical pole stands on a sloped platform. The bottom of the pole is used as the origin, O, of
a coordinate system in which the top, F, of the pole has coordinates (0 , 0 , 5.8). All units are
in metres.
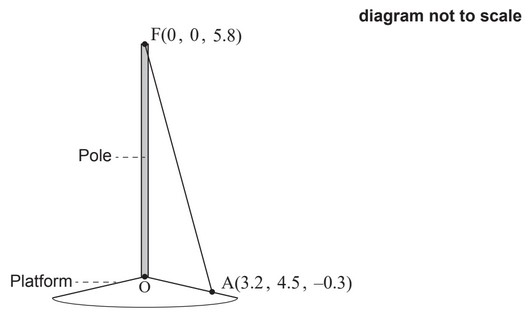
The pole is held in place by ropes attached at F.
One of these ropes is attached to the platform at point A(3.2, 4.5, −0.3). The rope forms a
straight line from A to F.
(a) Find \(\overrightarrow{AF}\)
(b) Find the length of the rope.
(c) Find \(F \widehat{A} O\), the angle the rope makes with the platform.
▶️Answer/Explanation
Ans:
Question
The diagram below shows a circle with centre O. The points A, B, C lie on the circumference of the circle and [AC] is a diameter.
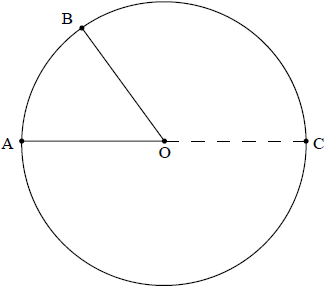
Let \(\overrightarrow {{\text{OA}}} = {\boldsymbol{a}}\) and \(\overrightarrow {{\text{OB}}} = {\boldsymbol{b}}\) .
a.Write down expressions for \(\overrightarrow {{\text{AB}}} \) and \(\overrightarrow {{\text{CB}}} \) in terms of the vectors \({\boldsymbol{a}}\) and \({\boldsymbol{b}}\) .[2]
b.Hence prove that angle \({\text{A}}\hat {\rm{B}}{\text{C}}\) is a right angle.[3]
▶️Answer/Explanation
Markscheme
\(\overrightarrow {{\text{AB}}} = {\boldsymbol{b}} – {\boldsymbol{a}}\) A1
\(\overrightarrow {{\text{CB}}} = {\boldsymbol{a}} + {\boldsymbol{b}}\) A1
[2 marks]
\(\overrightarrow {{\text{AB}}} \cdot \overrightarrow {{\text{CB}}} = \left( {{\boldsymbol{b}} – {\boldsymbol{a}}} \right) \cdot \left( {{\boldsymbol{b}} + {\boldsymbol{a}}} \right)\) M1
\( = {\left| {\mathbf{b}} \right|^2} – {\left| {\mathbf{a}} \right|^2}\) A1
\( = 0\) since \(\left| {\boldsymbol{b}} \right| = \left| {\boldsymbol{a}} \right|\) R1
Note: Only award the A1 and R1 if working indicates that they understand that they are working with vectors.
so \(\overrightarrow {{\text{AB}}} \) is perpendicular to \(\overrightarrow {{\text{CB}}} \) i.e. \({\text{A}}\hat {\rm{B}}{\text{C}}\) is a right angle AG
[3 marks]
Examiners report
This question was poorly done with most candidates having difficulties in using appropriate notation which made unclear the distinction between scalars and vectors. A few candidates scored at least one of the marks in (a) but most candidates had problems in setting up the proof required in (b) with many using a circular argument which resulted in a very poor performance in this part.
This question was poorly done with most candidates having difficulties in using appropriate notation which made unclear the distinction between scalars and vectors. A few candidates scored at least one of the marks in (a) but most candidates had problems in setting up the proof required in (b) with many using a circular argument which resulted in a very poor performance in this part.
Question
5. A ball is dropped from a height of 1.8 metres and bounces on the ground. The maximum
height reached by the ball, after each bounce, is 85% of the previous maximum height.
(a) Show that the maximum height reached by the ball after it has bounced for the sixth
time is 68cm, to the nearest cm.
(b) Find the number of times, after the first bounce, that the maximum height reached is
greater than 10cm.
(c) Find the total vertical distance travelled by the ball from the point at which it is dropped
until the fourth bounce.
▶️Answer/Explanation
Ans:
(a) use of geometric sequence with r = 0.85
EITHER
\((0.85)^6(1.8)\) OR 0.678869… OR \((0.85)^5 (1.53)\)
= 0.68m
= 68 cm
OR
\((0.85)^6(180)\) OR \((0.85)^5(153)\)
= 68 cm
(b) EITHER
\((0.85)^n (1.8) > 0.1\) OR \((0.85)^{n-1}(1.53)>0.1\)
17
OR
\((0.85)^{17}(1.8 = 0.114m\) and \((0.85)^{18}(1.8)=0.0966m\)
17
OR
solving \((0.85)^n(1.8)=0.1\) to find n = 17.8
17
(c) EITHER
distance (in one direction) travelled between first and fourth bounce
\(=\frac{(1.8 \times 0.86)(1-0.85^3)}{1-0.85}(=3.935925)\)
recognizing distances are travelled twice except first distance
1.8 + 2 (3.935925)
= 9.67 m (9.67185…m)
OR
distance (in one direction) travelled between drop and fourth bounce
\(=\frac{(1.8)(1-0.85^4)}{1-0.85}(=5.735925)\)
recognizing distances are travelled twice except first distance
2(5.735925)-1.8
= 9.67m (9.67185…m)
OR
distance (in one direction) travelled between first and fourth bounce
\((0.85)(1.8)+(0.85)^2(1.8) (=3.935925…)\)
recognizing distances are travelled twice except first distance
\(1.8+2(0.85)(1.8)+2(0.85)^2(1.8)+2(0.85)^3(1.8)\)
= 9.67m (9.67185…m)