Question
The diagram shows a sector, OAB, of a circle with centre O and radius r,
such that AÔB = θ.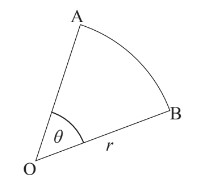
Sam measured the value of r to be 2 cm and the value of θ to be \(30^∘\).
(a) Use Sam’s measurements to calculate the area of the sector. Give your answer to
four significant figures.
It is found that Sam’s measurements are accurate to only one significant figure.
(b) Find the upper bound and lower bound of the area of the sector.
(c) Find, with justification, the largest possible percentage error if the answer to part (a)
is recorded as the area of the sector.
▶️Answer/Explanation
Ans:
(a) \(\pi \times 2^2 \times \frac{30}{360}\)
= 1.047 \(cm^2\)
(b) attempt to substitute any two values from 1.5, 2.5, 25 or 35 into area of sector formula
(upper bound = \(\pi \times 2.5^2 \times \frac{35}{360}=)\) 1.91 \(cm^2\) (1.90895….)
(lower bound = \(\pi \times 1.5^2 \times \frac{25}{360}=)\) 0.491 \(cm^2\) (0.490873…)
(c) \((\begin{vmatrix}
\frac{1.047-0.490873…}{0.490873…}
\end{vmatrix} \times 100=) 45.2 (%) (45.1532…)\)
\((\begin{vmatrix}
\frac{1.047-0.490873…}{0.490873…}
\end{vmatrix} \times 100=)113 (%) (113.293…)\)
so the largest percentage error is 113 %
Question
A circular disc is cut into twelve sectors whose areas are in an arithmetic sequence.
The angle of the largest sector is twice the angle of the smallest sector.
Find the size of the angle of the smallest sector.
▶️Answer/Explanation
Markscheme
METHOD 1
If the areas are in arithmetic sequence, then so are the angles. (M1)
\( \Rightarrow {S_n} = \frac{n}{2}(a + l) \Rightarrow \frac{{12}}{2}(\theta + 2\theta ) = 18\theta \) M1A1
\( \Rightarrow 18\theta = 2\pi \) (A1)
\(\theta = \frac{\pi }{9}\) (accept \(20^\circ \)) A1
[5 marks]
METHOD 2
\({{\text{a}}_{12}} = 2{a_1}\) (M1)
\(\frac{{12}}{2}({a_1} + 2{a_1}) = \pi {r^2}\) M1A1
\(3{a_1} = \frac{{\pi {r^2}}}{6}\)
\(\frac{3}{2}{r^2}\theta = \frac{{\pi {r^2}}}{6}\) (A1)
\(\theta = \frac{{2\pi }}{{18}} = \frac{\pi }{9}\) (accept \(20^\circ \)) A1
[5 marks]
METHOD 3
Let smallest angle = a , common difference = d
\(a + 11d = 2a\) (M1)
\(a = 11d\) A1
\({S_n} = \frac{{12}}{2}(2a + 11d) = 2\pi \) M1
\(6(2a + a) = 2\pi \) (A1)
\(18a = 2\pi \)
\(a = \frac{\pi }{9}\) (accept \(20^\circ \)) A1
[5 marks]
Question
The diagram shows a tangent, (TP) , to the circle with centre O and radius r . The size of \({\rm{P\hat OA}}\) is \(\theta \) radians.
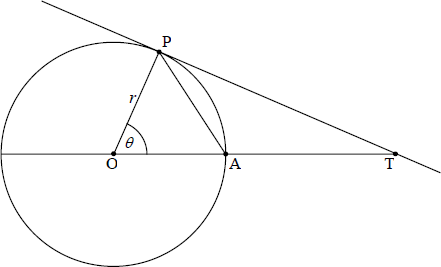
Find the area of triangle AOP in terms of r and \(\theta \) .[1]
Find the area of triangle POT in terms of r and \(\theta \) .[2]
Using your results from part (a) and part (b), show that \(\sin \theta < \theta < \tan \theta \) .[2]
▶️Answer/Explanation
Markscheme
area of \({\text{AOP}} = \frac{1}{2}{r^2}\sin \theta \) A1
[1 mark]
\({\text{TP}} = r\tan \theta \) (M1)
area of POT \( = \frac{1}{2}r(r\tan \theta )\)
\( = \frac{1}{2}{r^2}\tan \theta \) A1
[2 marks]
area of sector OAP \( = \frac{1}{2}{r^2}\theta \) A1
area of triangle OAP < area of sector OAP < area of triangle POT R1
\(\frac{1}{2}{r^2}\sin \theta < \frac{1}{2}{r^2}\theta < \frac{1}{2}{r^2}\tan \theta \)
\(\sin \theta < \theta < \tan \theta \) AG
[2 marks]
Question
From a vertex of an equilateral triangle of side \(2x\), a circular arc is drawn to divide the triangle into two regions, as shown in the diagram below.
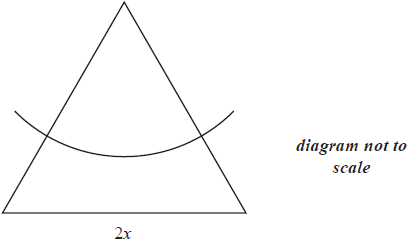
Given that the areas of the two regions are equal, find the radius of the arc in terms of x.
▶️Answer/Explanation
Markscheme
area of triangle \( = \frac{1}{2}{(2x)^2}\sin \frac{\pi }{3}\) (M1)
\( = {x^2}\sqrt 3 \) A1
Note: A \(0.5 \times {\text{base}} \times {\text{height}}\) calculation is acceptable.
area of sector \({\text{ = }}\frac{\theta }{2}{r^2} = \frac{\pi }{6}{r^2}\) (M1)A1
area of triangle is twice the area of the sector
\( \Rightarrow 2\left( {\frac{\pi }{6}{r^2}} \right) = {x^2}\sqrt 3 \) M1
\( \Rightarrow r = x\sqrt {\frac{{3\sqrt 3 }}{\pi }} \,\,\,\,\,\)or equivalent A1
[6 marks]
Question
The diagram below shows a circular lake with centre O, diameter AB and radius 2 km.
Jorg needs to get from A to B as quickly as possible. He considers rowing to point P and then walking to point B. He can row at \(3{\text{ km}}\,{{\text{h}}^{ – 1}}\) and walk at \(6{\text{ km}}\,{{\text{h}}^{ – 1}}\). Let \({\rm{P\hat AB}} = \theta \) radians, and t be the time in hours taken by Jorg to travel from A to B.
a.Show that \(t = \frac{2}{3}(2\cos \theta + \theta )\).[3]
b.Find the value of \(\theta \) for which \(\frac{{{\text{d}}t}}{{{\text{d}}\theta }} = 0\).[2]
c.What route should Jorg take to travel from A to B in the least amount of time?
Give reasons for your answer.[3]
▶️Answer/Explanation
Markscheme
angle APB is a right angle
\( \Rightarrow \cos \theta = \frac{{{\text{AP}}}}{4} \Rightarrow {\text{AP}} = 4\cos \theta \) A1
Note: Allow correct use of cosine rule.
\({\text{arc PB}} = 2 \times 2\theta = 4\theta \) A1
\(t = \frac{{{\text{AP}}}}{3} + \frac{{{\text{PB}}}}{6}\) M1
Note: Allow use of their AP and their PB for the M1.
\( \Rightarrow t = \frac{{4\cos \theta }}{3} + \frac{{4\theta }}{6} = \frac{{4\cos \theta }}{3} + \frac{{2\theta }}{3} = \frac{2}{3}(2\cos \theta + \theta )\) AG
[3 marks]
\(\frac{{{\text{d}}t}}{{{\text{d}}\theta }} = \frac{2}{3}( – 2\sin \theta + 1)\) A1
\(\frac{2}{3}( – 2\sin \theta + 1) = 0 \Rightarrow \sin \theta = \frac{1}{2} \Rightarrow \theta = \frac{\pi }{6}\) (or 30 degrees) A1
[2 marks]
\(\frac{{{{\text{d}}^2}t}}{{{\text{d}}{\theta ^2}}} = – \frac{4}{3}\cos \theta < 0\,\,\,\,\left( {{\text{at }}\theta = \frac{\pi }{6}} \right)\) M1
\( \Rightarrow t\) is maximized at \(\theta = \frac{\pi }{6}\) R1
time needed to walk along arc AB is \(\frac{{2\pi }}{6}{\text{ (}} \approx {\text{1 hour)}}\)
time needed to row from A to B is \(\frac{4}{3}{\text{ (}} \approx {\text{1.33 hour)}}\)
hence, time is minimized in walking from A to B R1
[3 marks]
Question
The logo, for a company that makes chocolate, is a sector of a circle of radius \(2\) cm, shown as shaded in the diagram. The area of the logo is \(3\pi {\text{ c}}{{\text{m}}^2}\).
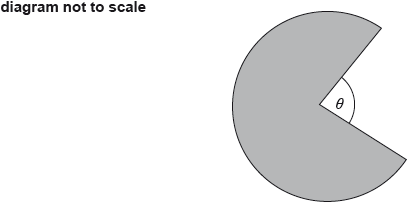
a.Find, in radians, the value of the angle \(\theta \), as indicated on the diagram.[3]
b.Find the total length of the perimeter of the logo.[2]
▶️Answer/Explanation
Markscheme
METHOD 1
\({\text{area}} = \pi {2^2} – \frac{1}{2}{2^2}\theta \;\;\;( = 3\pi )\) M1A1
Note: Award M1 for using area formula.
\( \Rightarrow 2\theta = \pi \Rightarrow \theta = \frac{\pi }{2}\) A1
Note: Degrees loses final A1
METHOD 2
let \(x = 2\pi – \theta \)
\({\text{area}} = \frac{1}{2}{2^2}x\;\;\;( = 3\pi )\) M1
\( \Rightarrow x = \frac{3}{2}\pi \) A1
\( \Rightarrow \theta = \frac{\pi }{2}\) A1
METHOD 3
Area of circle is \(4\pi \) A1
Shaded area is \(\frac{3}{4}\) of the circle (R1)
\( \Rightarrow \theta = \frac{\pi }{2}\) A1
[3 marks]
\({\text{arc length}} = 2\frac{{3\pi }}{2}\) A1
\({\text{perimeter}} = 2\frac{{3\pi }}{2} + 2 \times 2\)
\( = 3\pi + 4\) A1
[2 marks]
Total [5 marks]
Question
The following diagram shows a sector of a circle where \({\rm{A\hat OB}} = x\) radians and the length of the \({\text{arc AB}} = \frac{2}{x}{\text{ cm}}\).
Given that the area of the sector is \(16{\text{ c}}{{\text{m}}^2}\), find the length of the arc \(AB\).
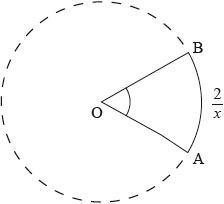
▶️Answer/Explanation
Markscheme
\({\text{arc length}} = \frac{2}{x} = rx\;\;\;\left( { \Rightarrow r = \frac{2}{{{x^2}}}} \right)\) M1
\(16 = \frac{1}{2}{\left( {\frac{2}{{{x^2}}}} \right)^2}x\;\;\;\left( { \Rightarrow \frac{2}{{{x^3}}} = 16} \right)\) M1
Note: Award M1s for attempts at the use of arc-length and sector-area formulae.
\(x = \frac{1}{2}\) A1
\({\text{arc length}} = {\text{4 (cm)}}\) A1
[4 marks]
