Question
Find the values of x for which the vectors \(\left( {\begin{array}{*{20}{c}}
1 \\
{2\cos x} \\
0
\end{array}} \right)\) and \(\left( {\begin{array}{*{20}{c}}
{ – 1} \\
{2\sin x} \\
1
\end{array}} \right)\) are perpendicular, \(0 \leqslant x \leqslant \frac{\pi }{2}\).
▶️Answer/Explanation
Markscheme
perpendicular when \(\left( {\begin{array}{*{20}{c}}
1 \\
{2\cos x} \\
0
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
{ – 1} \\
{2\sin x} \\
1
\end{array}} \right) = 0\) (M1)
\( \Rightarrow -1 + 4\sin x\cos x = 0\) A1
\( \Rightarrow \sin 2x = \frac{1}{2}\) M1
\( \Rightarrow 2x = \frac{\pi }{6},\frac{{5\pi }}{6}\)
\( \Rightarrow x = \frac{\pi }{{12}},\frac{{5\pi }}{{12}}\) A1A1
Note: Accept answers in degrees.
[5 marks]
Examiners report
Most candidates realised that the scalar product should be used to solve this problem and many obtained the equation \(4\sin x\cos x = 1\). Candidates who failed to see that this could be written as \(\sin 2x = 0.5\) usually made no further progress. The majority of those candidates who used this double angle formula carried on to obtain the solution \(\frac{\pi }{{12}}\) but few candidates realised that \(\frac{{5\pi }}{{12}}\) was also a solution.
Question
(a) Prove the trigonometric identity \(\sin (x + y)\sin (x – y) = {\sin ^2}x – {\sin ^2}y\).
(b) Given \(f(x) = \sin({x + \frac{\pi }{6}})\sin({x – \frac{\pi }{6}}),{\text{ }}x \in \left[ {0,{\text{ }}\pi } \right]\), find the range of \(f\).
(c) Given \(g(x) = \csc( {x + \frac{\pi }{6}})\csc( {x – \frac{\pi }{6}}),{\text{ }}x \in \left[ {0,{\text{ }}\pi } \right],{\text{ }}x \ne \frac{\pi }{6},{\text{ }}x \ne \frac{{5\pi }}{6}\), find the range of \(g\).
▶️Answer/Explanation
Markscheme
(a) \(\sin (x + y)\sin (x – y)\)
\( = (\sin x\cos y + \cos x\sin y)(\sin x\cos y – \cos x\sin y)\) M1A1
\( = {\sin ^2}x{\cos ^2}y + \sin x\sin y\cos x\cos y – \sin x\sin y\cos x\cos y – {\cos ^2}x{\sin ^2}y\)
\( = {\sin ^2}x{\cos ^2}y – {\cos ^2}x{\sin ^2}y\) A1
\( = {\sin ^2}x(1 – {\sin ^2}y) – {\sin ^2}y(1 – {\sin ^2}x)\) A1
\( = {\sin ^2}x – {\sin ^2}x{\sin ^2}y – {\sin ^2}y + {\sin ^2}x{\sin ^2}y\)
\( = {\sin ^2}x – {\sin ^2}y\) AG
[4 marks]
(b) \(f(x) = {\sin ^2}x – \frac{1}{4}\)
range is \(f \in \left[ { – \frac{1}{4},{\text{ }}\frac{3}{4}} \right]\) A1A1
Note: Award A1 for each end point. Condone incorrect brackets.
[2 marks]
(c) \(g(x) = \frac{1}{{{{\sin }^2}x – \frac{1}{4}}}\)
range is \(g \in \left] { – \infty ,{\text{ }} – 4} \right] \cup \left[ {\frac{4}{3},{\text{ }}\infty } \right[\) A1A1
Note: Award A1 for each part of range. Condone incorrect brackets.
[2 marks]
Total [8 marks]
Examiners report
Part a) often proved to be an easy 4 marks for candidates. A number were surprisingly content to gain the first 3 marks but were unable to make the final step by substituting \(1 – {\sin ^2}y\) for \({\cos ^2}y\).
Parts b) and c) were more often than not, problematic. Some puzzling ‘working’ was often seen, with candidates making little headway. Otherwise good candidates were able to answer part b), though correct solutions for c) were a rarity. The range \(g \in \left[ { – 4,{\text{ }}\frac{4}{3}} \right]\) was sometimes seen, but gained no marks.
Question
Consider the functions \(f(x) = \tan x,{\text{ }}0 \le \ x < \frac{\pi }{2}\) and \(g(x) = \frac{{x + 1}}{{x – 1}},{\text{ }}x \in \mathbb{R},{\text{ }}x \ne 1\).
a.Find an expression for \(g \circ f(x)\), stating its domain.[2]
b.Hence show that \(g \circ f(x) = \frac{{\sin x + \cos x}}{{\sin x – \cos x}}\).[2]
c.Let \(y = g \circ f(x)\), find an exact value for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) at the point on the graph of \(y = g \circ f(x)\) where \(x = \frac{\pi }{6}\), expressing your answer in the form \(a + b\sqrt 3 ,{\text{ }}a,{\text{ }}b \in \mathbb{Z}\).[6]
d.Show that the area bounded by the graph of \(y = g \circ f(x)\), the \(x\)-axis and the lines \(x = 0\) and \(x = \frac{\pi }{6}\) is \(\ln \left( {1 + \sqrt 3 } \right)\).[6]
▶️Answer/Explanation
Markscheme
\(g \circ f(x) = \frac{{\tan x + 1}}{{\tan x – 1}}\) A1
\(x \ne \frac{\pi }{4},{\text{ }}0 \le x < \frac{\pi }{2}\) A1
[2 marks]
\(\frac{{\tan x + 1}}{{\tan x – 1}} = \frac{{\frac{{\sin x}}{{\cos x}} + 1}}{{\frac{{\sin x}}{{\cos x}} – 1}}\) M1A1
\( = \frac{{\sin x + \cos x}}{{\sin x – \cos x}}\) AG
[2 marks]
METHOD 1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{(\sin x – \cos x)(\cos x – \sin x) – (\sin x + \cos x)(\cos x + \sin x)}}{{{{(\sin x – \cos x)}^2}}}\) M1(A1)
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{(2\sin x\cos x – {{\cos }^2}x – {{\sin }^2}x) – (2\sin x\cos x + {{\cos }^2}x + {{\sin }^2}x)}}{{{{\cos }^2}x + {{\sin }^2}x – 2\sin x\cos x}}\)
\( = \frac{{ – 2}}{{1 – \sin 2x}}\)
Substitute \(\frac{\pi }{6}\) into any formula for \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1
\(\frac{{ – 2}}{{1 – \sin \frac{\pi }{3}}}\)
\( = \frac{{ – 2}}{{1 – \frac{{\sqrt 3 }}{2}}}\) A1
\( = \frac{{ – 4}}{{2 – \sqrt 3 }}\)
\( = \frac{{ – 4}}{{2 – \sqrt 3 }}\left( {\frac{{2 + \sqrt 3 }}{{2 + \sqrt 3 }}} \right)\) M1
\( = \frac{{ – 8 – 4\sqrt 3 }}{1} = – 8 – 4\sqrt 3 \) A1
METHOD 2
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{(\tan x – 1){{\sec }^2}x – (\tan x + 1){{\sec }^2}x}}{{{{(\tan x – 1)}^2}}}\) M1A1
\( = \frac{{ – 2{{\sec }^2}x}}{{{{(\tan x – 1)}^2}}}\) A1
\( = \frac{{ – 2{{\sec }^2}\frac{\pi }{6}}}{{{{\left( {\tan \frac{\pi }{6} – 1} \right)}^2}}} = \frac{{ – 2\left( {\frac{4}{3}} \right)}}{{{{\left( {\frac{1}{{\sqrt 3 }} – 1} \right)}^2}}} = \frac{{ – 8}}{{{{\left( {1 – \sqrt 3 } \right)}^2}}}\) M1
Note: Award M1 for substitution \(\frac{\pi }{6}\).
\(\frac{{ – 8}}{{{{\left( {1 – \sqrt 3 } \right)}^2}}} = \frac{{ – 8}}{{\left( {4 – 2\sqrt 3 } \right)}}\frac{{\left( {4 + 2\sqrt 3 } \right)}}{{\left( {4 + 2\sqrt 3 } \right)}} = – 8 – 4\sqrt 3 \) M1A1
[6 marks]
Area \(\left| {\int_0^{\frac{\pi }{6}} {\frac{{\sin x + \cos x}}{{\sin x – \cos x}}{\text{d}}x} } \right|\) M1
\( = \left| {\left[ {\ln \left| {\sin x – \cos x} \right|} \right]_0^{\frac{\pi }{6}}} \right|\) A1
Note: Condone absence of limits and absence of modulus signs at this stage.
\( = \left| {\ln \left| {\sin \frac{\pi }{6} – \cos \frac{\pi }{6}} \right| – \ln \left| {\sin 0 – \cos 0} \right|} \right|\) M1
\( = \left| {\ln \left| {\frac{1}{2} – \frac{{\sqrt 3 }}{2}} \right| – 0} \right|\)
\( = \left| {\ln \left( {\frac{{\sqrt 3 – 1}}{2}} \right)} \right|\) A1
\( = – \ln \left( {\frac{{\sqrt 3 – 1}}{2}} \right) = \ln \left( {\frac{2}{{\sqrt 3 – 1}}} \right)\) A1
\( = \ln \left( {\frac{2}{{\sqrt 3 – 1}} \times \frac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}}} \right)\) M1
\( = \ln \left( {\sqrt 3 + 1} \right)\) AG
[6 marks]
Total [16 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
Question
a.Show that \(\cot \alpha = \tan \left( {\frac{\pi }{2} – \alpha } \right)\) for \(0 < \alpha < \frac{\pi }{2}\).[1]
b.Hence find \(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x,{\text{ }}0 < \alpha < \frac{\pi }{2}} \).[4]
▶️Answer/Explanation
Markscheme
EITHER
use of a diagram and trig ratios
eg,
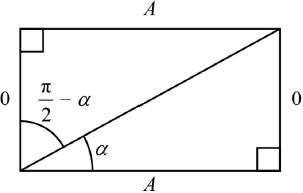
\(\tan \alpha = \frac{O}{A} \Rightarrow \cot \alpha = \frac{A}{O}\)
from diagram, \(\tan \left( {\frac{\pi }{2} – \alpha } \right) = \frac{A}{O}\) R1
OR
use of \(\tan \left( {\frac{\pi }{2} – \alpha } \right) = \frac{{\sin \left( {\frac{\pi }{2} – \alpha } \right)}}{{\cos \left( {\frac{\pi }{2} – \alpha } \right)}} = \frac{{\cos \alpha }}{{\sin \alpha }}\) R1
THEN
\(\cot \alpha = \tan \left( {\frac{\pi }{2} – \alpha } \right)\) AG
[1 mark]
\(\int_{\tan \alpha }^{\cot \alpha } {\frac{1}{{1 + {x^2}}}{\text{d}}x} = [\arctan x]_{\tan \alpha }^{\cot \alpha }\) (A1)
Note: Limits (or absence of such) may be ignored at this stage.
\( = \arctan (\cot \alpha ) – \arctan (\tan \alpha )\) (M1)
\( = \frac{\pi }{2} – \alpha – \alpha \) (A1)
\( = \frac{\pi }{2} – 2\alpha \) A1
[4 marks]
Examiners report
This was generally well done.
This was generally well done. Some weaker candidates tried to solve part (b) through use of a substitution, though the standard result \(\arctan x\) was well known. A small number used \(\arctan x + c\) and went on to obtain an incorrect final answer.
Question
[Maximum mark: 6]
Let f (x) = sin 2x and g(x) = sin(0.5x) .
(a) Write down
(i) the minimum value of the function f
(ii) the period of the function g . [3]
(b) Consider the equation f (x) g(x) Find the number of solutions, for \(0\leq x\leq \frac{3\pi }{2}\)
▶️Answer/Explanation
Answer:
(a) (i) –1
(ii) 4π (accept 720°)
(b) 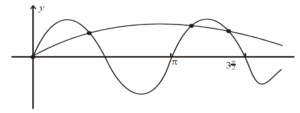
number of solutions: 4
