Question
Let f (x) = \(\sqrt{1+x}\) for x > -1 .
(a) Show that f (x)′′ = − \(\frac{1}{\sqrt[4]{(1+x)}^{3}}\) [3]
(b) Use mathematical induction to prove that f(n) (x) = \((-\frac{1}{4})^{n-1}\frac{(2n-3)!}{(n-2)!}(1+x)^{\frac{1}{2}-n}\)
for \(n\in \mathbb{Z}\;,n\geqslant 2\) [9]
Let g (x) = emx , m \(\in \mathbb{Q}\)
Consider the function h defined by h (x) = f (x) x g (x) for x > -1 .
It is given that the x2 term in the Maclaurin series for h (x) has a coefficient of \(\frac{7}{4}\)
(c) Find the possible values of m . [8]
▶️Answer/Explanation
Ans
(a)
attempt to use the chain rule
\(f'(x)= \frac{1}{2}(1+x)^{\frac{-1}{2}}\)
f”(x)= – \(\frac{1}{\sqrt[4]{(1+x)^3}}\)

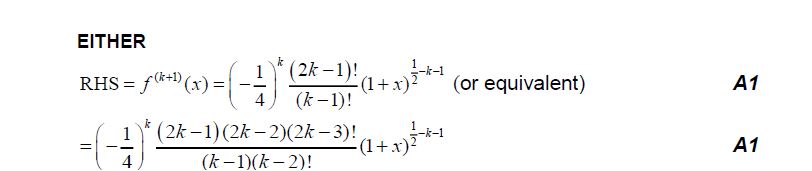






Question
Consider the function \(f\) defined by \(f(x) = {x^2} – {a^2},{\text{ }}x \in \mathbb{R}\) where \(a\) is a positive constant.
The function \(g\) is defined by \(g(x) = x\sqrt {f(x)} \) for \(\left| x \right| > a\).
a.i.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = f(x)\);[2]
a.ii.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \frac{1}{{f(x)}}\);[4]
a.iii.Showing any \(x\) and \(y\) intercepts, any maximum or minimum points and any asymptotes, sketch the following curves on separate axes.
\(y = \left| {\frac{1}{{f(x)}}} \right|\).[2]
b.Find \(\int {f(x)\cos x{\text{d}}x} \).[5]
c.By finding \(g'(x)\) explain why \(g\) is an increasing function.[4]
▶️Answer/Explanation
Markscheme
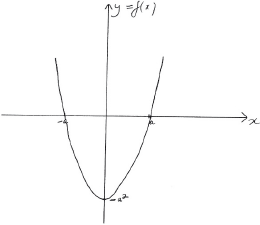
A1 for correct shape
A1 for correct \(x\) and \(y\) intercepts and minimum point
[2 marks]
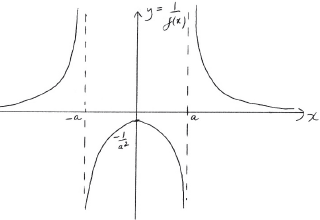
A1 for correct shape
A1 for correct vertical asymptotes
A1 for correct implied horizontal asymptote
A1 for correct maximum point
[??? marks]
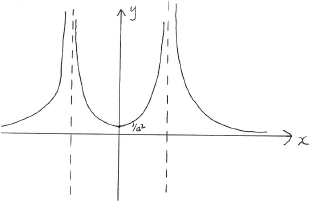
A1 for reflecting negative branch from (ii) in the \(x\)-axis
A1 for correctly labelled minimum point
[2 marks]
EITHER
attempt at integration by parts (M1)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = ({x^2} – {a^2})\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = ({x^2} – {a^2})\sin x + 2x\cos – 2\sin x + c\) A1
OR
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = \int {{x^2}\cos x{\text{d}}x – \int {{a^2}\cos x{\text{d}}x} } } \)
attempt at integration by parts (M1)
\(\int {{x^2}\cos x{\text{d}}x = {x^2}\sin x – \int {2x\sin x{\text{d}}x} } \) A1A1
\( = {x^2}\sin x – 2\left[ { – x\cos x + \int {\cos x{\text{d}}x} } \right]\) A1
\( = {x^2}\sin x + 2x\cos x – 2\sin x\)
\( – \int {{a^2}\cos x{\text{d}}x = – {a^2}\sin x} \)
\(\int {({x^2} – {a^2})\cos x{\text{d}}x = ({x^2} – {a^2})\sin x + 2x\cos x – 2\sin x + c} \) A1
[5 marks]
\(g(x) = x{({x^2} – {a^2})^{\frac{1}{2}}}\)
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + \frac{1}{2}x{({x^2} – {a^2})^{ – \frac{1}{2}}}(2x)\) M1A1A1
Note: Method mark is for differentiating the product. Award A1 for each correct term.
\(g'(x) = {({x^2} – {a^2})^{\frac{1}{2}}} + {x^2}{({x^2} – {a^2})^{ – \frac{1}{2}}}\)
both parts of the expression are positive hence \(g'(x)\) is positive R1
and therefore \(g\) is an increasing function (for \(\left| x \right| > a\)) AG
[4 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[N/A]
[N/A]
Question
The function f is defined, for \( – \frac{\pi }{2} \leqslant x \leqslant \frac{\pi }{2}\) , by \(f(x) = 2\cos x + x\sin x\) .
a.Determine whether f is even, odd or neither even nor odd.[3]
b.Show that \(f”(0) = 0\) .[2]
c.John states that, because \(f”(0) = 0\) , the graph of f has a point of inflexion at the point (0, 2) . Explain briefly whether John’s statement is correct or not.[2]
▶️Answer/Explanation
Markscheme
\(f( – x) = 2\cos ( – x) + ( – x)\sin ( – x)\) M1
\( = 2\cos x + x\sin x\,\,\,\,\,\left( { = f(x)} \right)\) A1
therefore f is even A1
[3 marks]
\(f'(x) = – 2\sin x + \sin x + x\cos x\,\,\,\,\,( = – \sin x + x\cos x)\) A1
\(f”(x) = – \cos x + \cos x – x\sin x\,\,\,\,\,( = – x\sin x)\) A1
so \(f”(0) = 0\) AG
[2 marks]
John’s statement is incorrect because
either; there is a stationary point at (0, 2) and since f is an even function and therefore symmetrical about the y-axis it must be a maximum or a minimum
or; \(f”(x)\) is even and therefore has the same sign either side of (0, 2) R2
[2 marks]
Examiners report
[N/A]
[N/A]
[N/A]
[MAI 5.8] MONOTONY – CONCAVITY – OPTIMIZATION-lala-ready
Question
[Maximum mark: 12]
Differentiate the following functions and hence determine whether each function is
increasing or decreasing (or neither).
(i) \(f(x)=x^{5}+e^{x}+1\), (ii) \(f(x)=x^{3}+ln\;x, \;x>0\)
(iii) \(f(x)=5-3e^{2x}\) (iv) \(f(x)=\frac{e^{x}-1}{e^{x}+1}\)
▶️Answer/Explanation
Ans.
(i) \({f}'(x)=5x^{4}+e^{x}>0\), \(f\) increasing (ii) \({f}'(x)=3x^{2}+\frac{1}{x}>0\), \(f\) increasing
(iii) \({f}'(x)=-6e^{2x}<0\), \(f\) decreasing (iv) \({f}'(x)=\frac{2e^{x}}{(e^{x}+1)^{2}}>0\), \(f\) increasing
Question
[Maximum mark: 8]
Consider \(f(x)=\frac{1}{3}x^{3}+2x^{2}-5x\). Part of the graph of \(f\) is shown below. There is a
maximum point at M, and a point of inflexion at N.
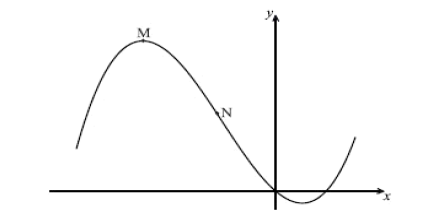
(a) Find \({f}'(x)\)
(b) Find the x – coordinate of M.
(c) Find the x – coordinate of N.
(d) Write down the equation of the normal line at M .
▶️Answer/Explanation
Ans.
(a)\({f}'(x)=x^{2}+4x-5\)
(b)\({f}'(x)=0\Leftrightarrow x=-5\), \(x=1\)
so \(x=-5\)
(c) \({f}”(x)=2x+4\)
2x+4=0
\(x=-2\)
(d) \(x=-5\)
