(a)

\( (f \circ g)(x) = 2 \tan x – \tan^3 x \) (M1A1, N2).

Working:
Given: \( f(x) = 2x – x^3 \), \( g(x) = \tan x \).
Composition: \( (f \circ g)(x) = f(g(x)) \).
Substitute: \( f(\tan x) = 2 \times \tan x – (\tan x)^3 \).
Simplify: \( 2 \tan x – \tan^3 x \). (M1 for substitution, A1 for answer)

[2 marks]

(b)

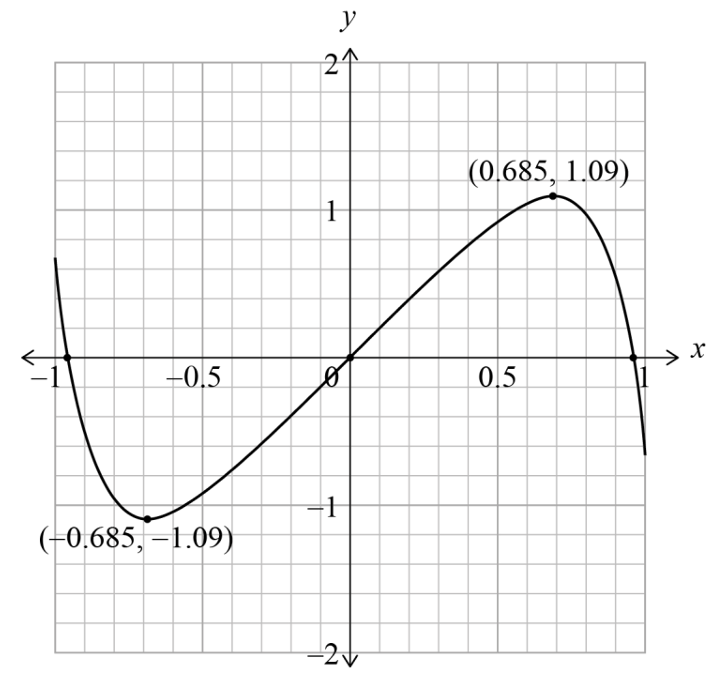
Local max at \( (0.685, 1.09) \), local min at \( (-0.685, -1.09) \) (A1A1A1, N3).

Working:
Function: \( y = 2 \tan x – \tan^3 x \).
Properties: Odd function, passes through \( (0,0) \).
Domain: \( -1 \leq x \leq 1 \), asymptotes at \( x = \pm \frac{\pi}{2} \approx \pm 1.571 \) are outside.
Find extrema: Derivative \( y’ = 2 \sec^2 x – 3 \tan^2 x \sec^2 x \).
Factor: \( y’ = \sec^2 x \times (2 – 3 \tan^2 x) \).
Set \( y’ = 0 \): \( 2 – 3 \tan^2 x = 0 \).
Solve: \( \tan^2 x = \frac{2}{3} \), \( \tan x = \pm \sqrt{\frac{2}{3}} \approx \pm 0.8165 \).
\( x \approx \pm 0.685 \) radians.
Evaluate: \( y(0.685) \approx 2 \times 0.8165 – (0.8165)^3 \approx 1.09 \).
\( y(-0.685) \approx -1.09 \).
Second derivative test confirms: Local max at \( x \approx 0.685 \), min at \( x \approx -0.685 \).
Graph features: Passes through \( (0,0) \), increases to max at \( (0.685, 1.09) \), decreases to min at \( (-0.685, -1.09) \).
Note: Graph is an odd function passing through the origin, with max above \( y = 1 \), min below \( y = -1 \), endpoints at \( x = \pm 1 \) with \( y \) in \([0.6, 0.8]\) and \([-0.8, -0.6]\), max at \( (0.685, 1.09) \), min at \( (-0.685, -1.09) \). (A1 for correct shape, A1 for endpoints, A1 for max/min coordinates)

[3 marks]

Total [5 marks]