Question 5. [Maximum mark: 6]
The functions f and g are defined for\( x\epsilon R \) by \(f\left ( x \right )=6x^{2}-12x+1\) and \(g\left ( x \right )=-x+c\) where \(c\epsilon R\)
(a) Find the range of f .
(b) Given that \( \left ( gof \right )\left ( x \right )\leq 0 \) for all \( x\epsilon R\), determine the set of possible values for c .
Answer/Explanation
(a) attempting to find the vertex
x=1 Or y=-5 OR f\left ( x \right )=6\left ( x-1 \right )^{2}-5 range is \(y\geq -5\)
(b) METHOD 1
\(\left ( gof \right )\left ( x \right )=-\left ( 6x^{2} -12x+1\right )+c\left ( =-\left ( 6\left ( x-1 \right )^{2} -5\right ) +c\right )\)
EITHER
relating to the range of f OR attempting to find g(-5) \(5+c\leq 0\)
OR
attempting to find the discriminant of \(\left ( gof \right )\left ( x \right )\)
\(144+24\left ( c-1 \right )\leq 0\left ( 120+24c\leq 0 \right )\)
THEN
\(c\leq -5\)
METHOD 2
vertical reflection followed by vertical shift new vertex is (1,5+c)
\(5+c\leq 0\)
\(c\leq -5\)
Question
Let f (x) = 4 – x3 and g(x) = lnx , for x >0 .
Find (f °g)(x). [2]
(i) Solve the equation (f °g)(x)= x
(ii) Hence or otherwise, given that g(2a) = f -1 (2a), , find the value of a . [5]
Answer/Explanation
Ans


Question
The graph of y = f (x) for -4 ≤ x ≤ 6 is shown in the following diagram.
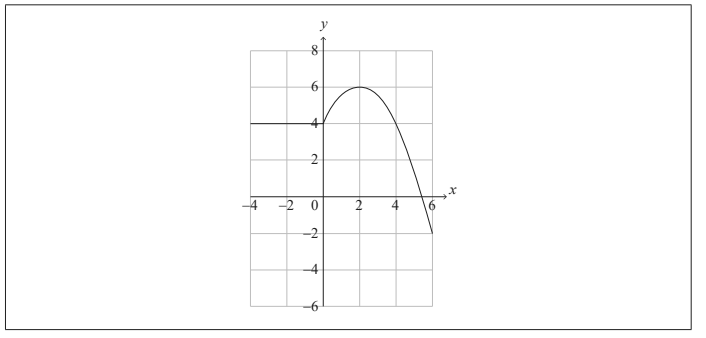
(a) Write down the value of
(i) f (2) ;
(ii) ( f o f )(2) . [2]
(b) Let g(x) = \(\frac{1}{2} f (x) +1\) for -4 ≤ x ≤ 6 . On the axes above, sketch the graph of g . [3]
Answer/Explanation
Ans:
(a) (i) f(2) = 6
(ii) (fof)2=− 2 [2 marks]
(b) 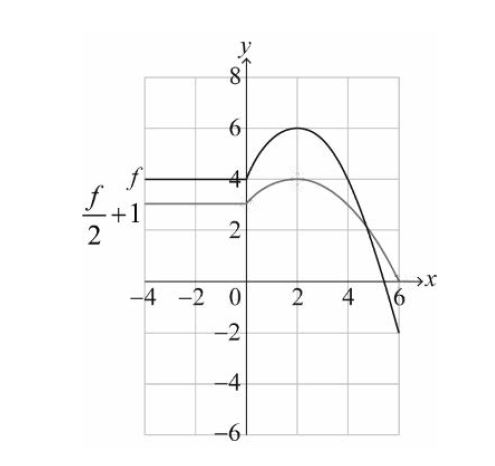
Question
The functions f and g are defined as:
\[f(x) = {{\text{e}}^{{x^2}}},{\text{ }}x \geqslant 0\]
\[g(x) = \frac{1}{{x + 3}},{\text{ }}x \ne – 3.\]
(a) Find \(h(x){\text{ where }}h(x) = g \circ f(x)\) .
(b) State the domain of \({h^{ – 1}}(x)\) .
(c) Find \({h^{ – 1}}(x)\) .
Answer/Explanation
Markscheme
(a) \(h(x) = g \circ f(x) = \frac{1}{{{{\text{e}}^{{x^2}}} + 3}},{\text{ }}(x \geqslant 0)\) (M1)A1
(b) \(0 < x \leqslant \frac{1}{4}\) A1A1
Note: Award A1 for limits and A1 for correct inequality signs.
(c) \(y = \frac{1}{{{{\text{e}}^{{x^2}}} + 3}}\)
\(y{{\text{e}}^{{x^2}}} + 3y = 1\) M1
\({{\text{e}}^{{x^2}}} = \frac{{1 – 3y}}{y}\) A1
\({x^2} = \ln \frac{{1 – 3y}}{y}\) M1
\(x = \pm \sqrt {\ln \frac{{1 – 3y}}{y}} \)
\( \Rightarrow {h^{ – 1}}(x) = \sqrt {\ln \frac{{1 – 3x}}{x}} {\text{ }}\left( { = \sqrt {\ln \left( {\frac{1}{x} – 3} \right)} } \right)\) A1
[8 marks]
Question
Let \(f(x) = \frac{4}{{x + 2}},{\text{ }}x \ne – 2{\text{ and }}g(x) = x – 1\).
If \(h = g \circ f\) , find
(a) h(x) ;
(b) \({h^{ – 1}}(x)\) , where \({h^{ – 1}}\) is the inverse of h.
Answer/Explanation
Markscheme
(a) \(h(x) = g\left( {\frac{4}{{x + 2}}} \right)\) (M1)
\( = \frac{4}{{x + 2}} – 1\,\,\,\,\,\left( { = \frac{{2 – x}}{{2 + x}}} \right)\) A1
(b) METHOD 1
\(x = \frac{4}{{y + 2}} – 1\,\,\,\,\,\)(interchanging x and y) M1
Attempting to solve for y M1
\((y + 2)(x + 1) = 4\,\,\,\,\,\left( {y + 2 = \frac{4}{{x + 1}}} \right)\) (A1)
\({h^{ – 1}}(x) = \frac{4}{{x + 1}} – 2\,\,\,\,\,(x \ne – 1)\) A1 N1
METHOD 2
\(x = \frac{{2 – y}}{{2 + y}}\,\,\,\,\,\)(interchanging x and y) M1
Attempting to solve for y M1
\(xy + y = 2 – 2x\,\,\,\,\,\left( {y(x + 1) = 2(1 – x)} \right)\) (A1)
\({h^{ – 1}}(x) = \frac{{2(1 – x)}}{{x + 1}}\,\,\,\,\,(x \ne – 1)\) A1 N1
Note: In either METHOD 1 or METHOD 2 rearranging first and interchanging afterwards is equally acceptable.
[6 marks]
Question
Shown below are the graphs of \(y = f(x)\) and \(y = g(x)\).
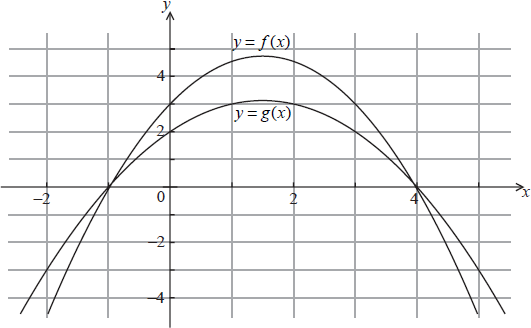
If \((f \circ g)(x) = 3\), find all possible values of x.
Answer/Explanation
Markscheme
\(g(x) = 0{\text{ or 3}}\) (M1)(A1)
x = –1 or 4 or 1 or 2 A1A1
Notes: Award A1A1 for all four correct values,
A1A0 for two or three correct values,
A0A0 for less than two correct values.
Award M1 and corresponding A marks for correct attempt to find expressions for f and g.
[4 marks]
Question
[Maximum mark: 9] [with / without GDC]
The function \(f\) is given by \(f(x)=x^{2}-6x+13\), for \(x\geq 3\).
(a) Show that \(f\) may also be written in the form \(f(x)=(x-3)^{2}+4\).
(b) Hence find the inverse function f –1.
(c) State the domain and the range of \(f\) .
(d) State the domain and the range of f–1.
Answer/Explanation
(a) \(f(x)=(x-3)^{2}+4=x^{2}-6x+9+4=x^{2}-6x+13\)
(b) \(y=(x-3)^{2}+4\)
\(y-4=(x-3)^{2}\)
\(\sqrt{y-4}=x-3\)
\(\sqrt{y-4}+3=x\)
\(\Rightarrow f^{-1}(x)=\sqrt{x-4}+3\)
(c) x ≥ 3 and y ≥ 4
(d) x ≥ 4 and y ≥ 3
