Question
Let \(f(x) = A{{\rm{e}}^{kx}} + 3\) . Part of the graph of f is shown below.
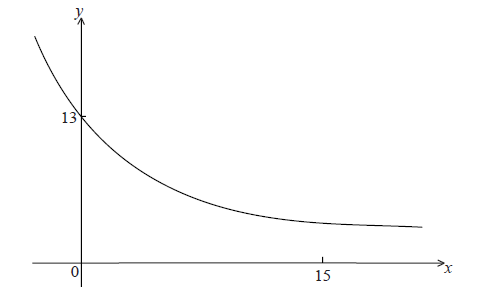
The y-intercept is at (0, 13) .
Show that \(A = 10\) .
Given that \(f(15) = 3.49\) (correct to 3 significant figures), find the value of k.
(i) Using your value of k , find \(f'(x)\) .
(ii) Hence, explain why f is a decreasing function.
(iii) Write down the equation of the horizontal asymptote of the graph f .
Let \(g(x) = – {x^2} + 12x – 24\) .
Find the area enclosed by the graphs of f and g .
Answer/Explanation
Markscheme
substituting (0, 13) into function M1
e.g. \(13 = A{{\rm{e}}^0} + 3\)
\(13 = A + 3\) A1
\(A = 10\) AG N0
[2 marks]
substituting into \(f(15) = 3.49\) A1
e.g. \(3.49 = 10{{\rm{e}}^{15k}} + 3\) , \(0.049 = {{\rm{e}}^{15k}}\)
evidence of solving equation (M1)
e.g. sketch, using \(\ln \)
\(k = – 0.201\) (accept \(\frac{{\ln 0.049}}{{15}}\) ) A1 N2
[3 marks]
(i) \(f(x) = 10{{\rm{e}}^{ – 0.201x}} + 3\)
\(f(x) = 10{{\rm{e}}^{ – 0.201x}} \times – 0.201\) \(( = – 2.01{{\rm{e}}^{ – 0.201x}})\) A1A1A1 N3
Note: Award A1 for \(10{{\rm{e}}^{ – 0.201x}}\) , A1 for \( \times – 0.201\) , A1 for the derivative of 3 is zero.
(ii) valid reason with reference to derivative R1 N1
e.g. \(f'(x) < 0\) , derivative always negative
(iii) \(y = 3\) A1 N1
[5 marks]
finding limits \(3.8953 \ldots \), \(8.6940 \ldots \) (seen anywhere) A1A1
evidence of integrating and subtracting functions (M1)
correct expression A1
e.g. \(\int_{3.90}^{8.69} {g(x) – f(x){\rm{d}}x} \) , \(\int_{3.90}^{8.69} {\left[ {\left( { – {x^2} + 12x – 24} \right) – \left( {10{{\rm{e}}^{ – 0.201x}} + 3} \right)} \right]} {\rm{d}}x\)
area \(= 19.5\) A2 N4
[6 marks]
Question
The number of bacteria, n , in a dish, after t minutes is given by \(n = 800{{\rm{e}}^{0.13t}}\) .
Find the value of n when \(t = 0\) .
Find the rate at which n is increasing when \(t = 15\) .
Answer/Explanation
Markscheme
\(n = 800{{\rm{e}}^0}\) (A1)
\(n = 800\) A1 N2
[2 marks]
evidence of using the derivative (M1)
\(n'(15) = 731\) A1 N2
[2 marks]
METHOD 1
setting up inequality (accept equation or reverse inequality) A1
e.g. \(n'(t) > 10000\)
evidence of appropriate approach M1
e.g. sketch, finding derivative
\(k = 35.1226 \ldots \) (A1)
least value of k is 36 A1 N2
METHOD 2
\(n'(35) = 9842\) , and \(n'(36) = 11208\) A2
least value of k is 36 A2 N2
[4 marks]
Question
The price of a used car depends partly on the distance it has travelled. The following table shows the distance and the price for seven cars on 1 January 2010.

The relationship between \(x\) and \(y\) can be modelled by the regression equation \(y = ax + b\).
On 1 January 2010, Lina buys a car which has travelled \(11\,000{\text{ km}}\).
The price of a car decreases by 5% each year.
Lina will sell her car when its price reaches \(10\,000\) dollars.
(i) Find the correlation coefficient.
(ii) Write down the value of \(a\) and of \(b\).
Use the regression equation to estimate the price of Lina’s car, giving your answer to the nearest 100 dollars.
Calculate the price of Lina’s car after 6 years.
Find the year when Lina sells her car.
Answer/Explanation
Markscheme
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
(i) valid approach (M1)
eg\(\,\,\,\,\,\)correct value for \(r\) (or for \(a\) or \(b\) seen in (ii))
\( – 0.994347\)
\(r = – 0.994\) A1 N2
(ii) \( – 1.58095,{\text{ }}33480.3\)
\(a = – 1.58,{\text{ }}b = 33500\) A1A1 N2
[4 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
correct substitution into their regression equation
eg\(\,\,\,\,\,\)\( – 1.58095(11000){\text{ }} + 33480.3\) (A1)
\(16\,089.85{\text{ }}(16\,120{\text{ from 3sf}})\) (A1)
\({\text{price}} = 16\,100{\text{ }}({\text{dollars}})\) (must be rounded to the nearest 100 dollars) A1 N3
[3 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\(P \times {({\text{rate}})^t}\)
\({\text{rate}} = 0.95\) (may be seen in their expression) (A1)
correct expression (A1)
eg\(\,\,\,\,\,\)\(16100 \times {0.95^6}\)
\(11\,834.97\)
\(11\,800{\text{ }}({\text{dollars}})\) A1 N2
METHOD 2
attempt to find all six terms (M1)
eg\(\,\,\,\,\,\)\(\left( {\left( {(16\,100 \times 0.95) \times 0.95} \right) \ldots } \right) \times 0.95\), table of values
5 correct values (accept values that round correctly to the nearest dollar)
\(15\,295,{\text{ }}14\,530,{\text{ }}13\,804,{\text{ }}13\,114,{\text{ }}12\,458\) A2
\(11\,835\)
\(11\,800{\text{ }}({\text{dollars}})\) A1 N2
[4 marks]
Note: There may be slight differences in answers, depending on which values candidates carry through in subsequent parts. Accept answers that are consistent with their working.
METHOD 1
correct equation (A1)
eg\(\,\,\,\,\,\)\(16\,100 \times {0.95^x}{\text{ = }}10\,000\)
valid attempt to solve (M1)
eg\(\,\,\,\,\,\) , using logs
, using logs
9.28453 (A1)
year 2019 A1 N2
METHOD 2
valid approach using table of values (M1)
both crossover values (accept values that round correctly to the nearest dollar) A2
eg\(\,\,\,\,\,\)\({\text{P}} = 10\,147{\text{ }}({\text{1 Jan 2019}}),{\text{ P}} = 9\,639.7{\text{ }}({\text{1 Jan 2020}})\)
year 2019 A1 N2
[4 marks]
